Keywords

1 Introduction

During the last years, the interest in the switched reluctance motor (SRM) has increased due to their manufacturing simplicity, large speed range, fault-tolerant operation and essentially for the non-use of rare elements in both the rotor and the stator. Due to these advantages, in the future this motor may be preferable compared to the induction and synchronous motor. However, there are still some disadvantages to solve originated by the operating process of the motor, namely the produced torque ripple component and audible acoustic noise.

These disadvantages can be greatly reduced by an adequate control, which is the main topic of this PhD work. A scalable controller is proposed with three subparts, the speed controller, the current reference generator and the current controller. The speed controller is not addressed in this study. For systems where the electrical time constant is much smaller than the mechanical time constant, the current control loop must be treated as an ideal current source, i.e. given a set-point current, it will be tracked immediately. With this assumption, any linear control design technique can be used for speed control. The current reference generator is the connection between torque and current reference, and due to the motor’s highly non-linearity, this process may not be a straightforward issue. These two subparts will be a matter for future work.

For now, the current controller subpart is our main focus. As the traditional controllers, such as linear PI and hysteresis, cannot achieve the performance level we wish, an initial study of the model predictive control is carried out for this subpart of the controller. The research findings of this study are expected to build a solid foundation for better development in next research phase, which is generically supported by the following questions.

1.1 Research Questions

Why and how can the model predictive control (MPC) to the switched reluctance motor drive be implement? To successfully answer this question, the problem may be divide into some sub questions.

  • Why do we place the MPC at the heart of our research?

In previous work, traditional controllers like PI and hysteresis control were used [1]. Although they are the most used in the literature, their performance may not be sufficient. For example, in the case of PI control, in order to achieve the best performance, it would be necessary to know exactly how the machine behaves at every operating point. For the hysteresis control, it would be necessary to increase the switching frequency. And neither the behavior of the machine is exactly known nor we want to increase the switching frequency. Further investigation is thus certainly warranted.

The major difference between these traditional controllers’ whit the MPC is that they work by looking to the past to decide a converter state to get the system close to the reference, while the MPC looks forward to decide the best converter state that will approximate the system to the reference. In other words, the MPC knows in advance what is expected to happen.

  • Is this control suitable for high frequency operations?

Looking to the past, from at least 20 years ago, the control systems started to have been completely based on digital controllers. It started with simple microprocessors, then the microcontrollers came about and then by the digital signal processors (DSP) [2]. Nowadays, even hybrid solutions using microprocessors and field programmable gate arrays are an option [3]. These innovations allow the use of heavy methods, not only for control but also for prediction, filtering and data saving. Neural controllers and Kalman filters are examples of heavy processing methods used in DSP’s.

  • Which state should be predicted and which constraints are related?

From the viewpoint of controllability of the SRM, the machine state variables that can be predicted are the torque, flux or current. In all of them have pros and cons in their implementation. The torque is the one we want to control in order to keep it constant, while the problem is in its estimation. As the SRM model is highly nonlinear, it makes the torque estimation a quite difficult task, and is only possible by using the machine characteristics in tables or approximated by functions. Also, the characteristic may change during the motor operation leading to loss of accuracy of the estimation. The same happens when the flux is used as state variable, as it is necessary to know the flux-current characteristic to convert current and rotor position into flux.

The use of the current as state variable has the advantage of directly controlling the state that is measured. However, the problem is similar because it is necessary to know the inductance characteristic of the machine for the prediction.

This paper is organized as it follows. In Sect. 2 the relationship to technological innovation for life improvement is addressed. A synthesis of the state of the art is then presented in Sect. 3 and the model of the SRM and power converter are the topics of discussion in Sect. 4. Section 5 proposes the current control solution based on predictive control technique, followed by simulation results in Sect. 6. Finally, Sect. 7 concludes the paper and indicates guidelines for future work.

2 Contribution to Life Improvement

According to the European Green Deal, Europe has to become climate-neutral by the year of 2050 in order to improve the well-being of people [4]. This objective aims to take effect not only in the energy sector but also in household appliances, in the industry and in public and private mobility. Electric motors play an important role in all of these sectors, so motor efficiency and reliability are always of great concern.

Transitioning to a low-carbon society is vital to improve the quality of life in different dimensions and realizing sustainable development. Improving products efficiency and creating reliable solutions are an important part of this process. In this line, the SRM may play an important role for different products due its advantages, such as reliability. Since the motor has no windings or rare rotor elements, it is free from electromagnetic rotor failures and no rotor cooling is required. As the stator phases are independent, a failure in one phase does not necessarily imply a system shutdown. Another advantage is being well suited for high-speed operation. Some applications like dry machines, machine tools and electric vehicles may need to work at high speeds, which is not a limitation for the SRM.

Considering the advantages of the SRM described, the main contribution of this PhD work for “Technological Innovation for Life Improvement” consists of the development of a high-performance, scalable-speed controller in order to reduce the torque ripple component and the acoustic noise. As a result, the proposed controller may contribute to mitigating some constraints and consequently the wider dissemination of SRM applications.

3 State of the Art

In the literature, the number of works using the model predictive control has been greatly increasing in the recent years. In [5], the basic principle of nonlinear MPC is reviewed, and advantages, disadvantages and implementation aspects are also discussed. Another good reference is the book [6], where the author approaches the method and describes the application of it to power converters and motor drives.

In general, the MPCs can be classified in current, flux and torque prediction. For example, in [7] and [8] a model predictive current control is implemented in order to reduce the torque ripple. In these works, the simulations are comparative and do not validate the method, preventing readers from evaluating the accuracy of the current prediction. In [9] and [10], the authors developed a scheme where the inductance profile in current prediction is updated throughout the operating process. For the flux prediction, in [11] the MPC is used together with the direct torque control method, and in [12] a virtual-flux MPC is created using the machine flux characteristic. Finally, for torque prediction, in [13] a nonlinear model is used to estimate and predict the instantaneous torque and in [14] the author uses an analytical model for torque estimation. Besides the controlled state is the torque itself, simulation results do not seem very effective. To sum up, only a few papers study the use of the MPC in the SRM, and provide few definitive answers, so further research is certainly warranted.

4 The Switched Reluctance Motor System

The SRM voltage and magnetic equations are expressed by:

$$ V = R_{s} .i + \frac{{d\Psi \left( {\uptheta,{\text{i}}} \right) }}{dt} $$
(1)
$$ \Psi \left( {\theta ,i} \right) = L\left( {\theta ,i} \right).i $$
(2)

where \( V \) is the supply voltage, \( R_{s} \) the stator resistance, \( i \) the current, \( \Psi \) the flux-linkage, \( \theta \) the rotor position and \( L \) the self-inductance.

The most used power converter for the SRM is the asymmetric bridge. Each converter phase is composed by two diodes and two transistors. It can feed the motor phase with the \( V_{DC} \) state by activating both transistors, \( - V_{DC} \) state while there is still current in the windings and by putting both transistors off, and the 0 V state by only activating one of the transistors, letting the current flow either in the top or bottom mesh. The advantages of this converter are the independent control by phase, unidirectional current and allowing current to the source voltage to regenerate.

5 Model Predictive Current Control of SRM

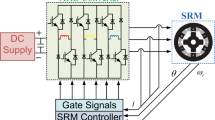
The proposed control scheme for the SRM drive is shown in Fig. 1. The control, the power converter and the motor are presented. This proposed solution is in a modular format, where the control can be separated into speed controller, current reference generator and current controller. In this study, our concern is to have an ideal solution for the current control so the speed controller and reference generator are not addressed. At first, it is assumed that there exists an outer control loop providing a desired current, \( i_{ref} \).

Fig. 1.
figure 1

Proposed block diagram.

Full size image

This input, of the current controller, is expected to have both a slow and fast dynamic in its waveform. To follow this unpredictable reference, the current control has to be fast and accurate. These characteristics can be found in the Finite Set Model Predictive Control, where its application to the SRM is the main contribution of this work.

5.1 Model Predictive Control for the SRM

For this system, the MPC is divided into a current prediction block, a self-inductance profile block and a cost function block. In the current prediction block a discretization of the model of the motor for the prediction of the future behavior of the current is required. This model is iteratively computed using each available inductance value with the measured mechanical position and stator phase current to estimate the future value of the stator current. With this information, the controller has the objective of determining which is the ideal voltage vector to apply in the next cycle in order to minimize the cost function. The one that has the minimum value is the converter state that is applied in the next cycle. The process is then repeated for each phase and for every cycle. In order to simplify the controller, the MPC time horizon is only designed for one sampling time.

5.2 Current Prediction

Using the Forward Euler method and rearranging the Eqs. (1) and (2) with some simplifications, the discrete equation is obtained

$$ i\left( {k + T} \right) = \frac{T}{L\left( k \right)}.\left[ {V^{*} \left( j \right) - R_{s} .i\left( k \right)} \right] + i\left( k \right) $$
(3)

where \( T \) is the sampling period, \( k \) is the actual sampling and \( V^{*} \left( j \right) \) is the voltage value for the converter state \( j \), as already seen \( V^{*} \left( j \right) \) can be equal to \( V_{DC} \), \( - V_{DC} \) or \( 0 \). The value of \( L\left( k \right) \) is from the self-inductance profile block, which is a table with the machine characteristic obtained by the finite element method.

5.3 Cost Function Minimization

Having estimated the current for all the converter states, the cost function is then calculated, which is simply the error module given by

$$ Error\left( j \right) = \left| {i_{ref} - i\left( {k + T,j} \right)} \right| $$
(4)

where \( i\left( {k + T,j} \right) \) is the current prediction at time \( k + T \) for the converter state \( j \). The state \( j \) that has the lowest error value is the one applied in the next cycle.

6 Simulations

In order to validate the proposed diagram block, a Matlab/Simulink® simulation environment was created. A number of simulations have been performed in order to evaluate the performance of the developed control technique. Table 1 shows the parameters used in the simulation studies.

Table 1. Simulation parameters.
Full size table

As the work is around the current control, it is simulated a scenario for two-step levels of acceleration. Figure 2 summarize the simulations results. There is a start-up transient under no-load, with current reference set to 5.5 A from time 0 s to time 0.05 s and of 2.5 A from time 0.05 s to time 0.2 s. The current reference is also multiplied by a sinusoidal waveform of small magnitude to represent the fast changes that the current reference can have. The mechanical speed, stator current responses and applied voltage are shown.

Fig. 2.
figure 2

Simulation results for two values of current.

Full size image

Good tracking of the current reference can be observed for both current levels. Even for the high frequency sinusoid component there is no problem for the controller, where the absolute current error percentage always being less than \( 10\% \). Looking at the zoom of the predicted and the real current it can be seen that they are close but not too much. This is due to less satisfactory precision of the self-inductance profile. Because of this, the control is somewhat aggressive, commutating several times between the \( V_{DC} \) and \( - V_{DC} \) states in the middle of phase conduction.

7 Conclusions and Further Work

In this work, a method for the current control of a switched reluctance motor, based on predictive control technique, was introduced. The method avoids the use of a modulation to command the asymmetric bridge converter, providing an accurate current control on the basis of the cost function and the discrete model of the motor.

The control scheme was studied and analyzed using a Matlab/Simulink® environment. Simulation results show the good performance of predictive current controller for tracking the current reference.

Further work, currently under way, includes improving the current prediction, which although already good, should be improved with estimation techniques, for example. The connection between the output of the speed controller and the reference current will be the second major part of this PhD work. In this part, it will be possible to manipulate the input signal in order to minimize the torque ripple as much as possible.