Keywords

1 Introduction

Graphs are useful to model complex systems in a broad range of domains. Among the approaches designed to study them, graph embedding has attracted a lot of interest in the scientific community. It consists in encoding parts of the graph (node, edge, substructure) or a whole graph into a low dimensional space while preserving structural properties. Because it allows all the range of data mining and machine learning techniques that require vectors as input to be applied to relational data, it can benefit a lot of applications.

Several surveys have been recently published [5, 6, 8, 20, 21], some of them including a comparative study of the performance of the methods to solve specific tasks. Among them, Cui et al. [6] propose a typology of network embedding methods into three families: matrix factorization, random walk and deep learning methods. Following the same typology, Goyal et al. [8] compare state of the art methods on few tasks such as link prediction, graph reconstruction or node classification and analyze the robustness of the algorithms with respect to hyper-parameters. Recently, Cai et al. [5] extended the typology by adding deep learning based methods without random walks but also two other families: graph kernel based methods notably helpful to represent the whole graph as a low-dimensional vector and generative models which provide a latent space as embedding space. For their part, Zhang et al. [21] classify embedding techniques into two types: unsupervised network representation learning or semi-supervised and they list a number of embedding methods depending on the information sources they use to learn. Like Goyal et al. [8], they compare the methods on different tasks. Finally, Hamilton et al. [10] introduce an encoder-decoder framework to describe representative embedding algorithms from a methodological perspective. In this framework, the encoder corresponds to the function which maps the elements of a graph as vectors. The decoder is a function which associates a specific graph statistic to the obtained vectors, for instance for a pair of node embeddings the decoder can give their similarity in the vector space, allowing the similarity of the nodes in the original graph to be quantified.

From this last work, we retained the encoder-decoder framework and we propose to use it for evaluating the different embedding methods. To that end, we compare, using metrics that we introduce, the value computed by the decoder with the value associated to the corresponding nodes in the graph for the equivalent function. Thus, in this paper, we adopt a different point of view from the previous task-oriented evaluations. Indeed, all of them consider embeddings as a black box, i.e., using obtained features without considering their properties. They ignore the fact that embedding algorithms are designed, explicitly or implicitly, to preserve some particular structural properties and their usefulness for a given task depends on how they succeed to capture it. Thus, in this paper, through an experimental comparative study, we compare the ability of embedding algorithms to capture specific properties, i.e., first-order proximity of nodes, structural equivalence (second-order proximity), isomorphic equivalence and community structure.

In Sect. 2, these topological properties are formally defined and measures are introduced to evaluate to what extent embedding methods encode them. Section 3 presents the studied embedding methods. Section 4 describes the datasets used for the experiments, while Sect. 5 presents the results.

2 Structural Properties and Metrics

There is a wide range of graph properties that are of interest. We propose to study several of them which are at the basis of network analysis and are directly linked with usual learning and mining tasks on graphs [13]. First, we measure the ability of an embedding method to recover the set of neighbors of the nodes which is the first-order proximity (P1). This property is important for several downstream tasks: clustering where vectors of the same cluster represent nodes of the same community, graph reconstruction where two similar vectors represent two nodes that are neighbors in the graph, and node classification based for instance on majority vote of the neighbors. Secondly, we evaluate the ability of embedding methods to capture the second-order proximity (P2) which is the fact that two nodes have the same set of neighbors. This property is especially interesting when dealing with link prediction since, in social graphs, it is assumed that two nodes that share the same friends are likely to become friends too. Thirdly, we measure how much an embedding method is able to capture the roles of nodes in a graph which is the isomorphic equivalence (P3). This property is interesting when looking for specific nodes like leaders or outsiders. Finally, we evaluate the ability of an embedding method to detect communities (P4) in a graph which has been an on going field of research for the last 20 years. Next, we define both properties and measures we use in order to quantify how much an embedding method is able to capture those properties.

Let G(V, E) be an unweighted and undirected graph where \(V=\{v_0,...,v_{n-1}\}\) is the set of n vertices, \(E=\{e_{ij}\}_{i,j=0}^{n-1}\) the set of m edges and A is its binary adjacency matrix. Graph embedding consists in encoding the graph into a low-dimensional space \(R^d\), where d is the dimension of the real space, with a function \( f :V \mapsto Y\) which maps vertices to vector embeddings while preserving some properties of the graph. We note \(Y \in \mathbb {R}^{n \times d}\) the embedding matrix and \(Y_i\) its i-th row representing the node \(v_i\).

Neighborhood or first-order proximity (P1): capturing the neighborhood for an embedding method means that it aims at keeping any two nodes \(v_i\) and \(v_j\) that are linked in the original graph (\(A_{ij}=1\)) close in the embedding space. The measure S designed for this property is based on the comparison between the set \(N(v_i)\) of neighbors in the graph of every node \(v_i\) and the set \(N_{E}\left( v_i\right) \) of its \(|N\left( v_i\right) |\) nearest neighbors in the embedding space where \(|N\left( v_i\right) |\) is its degree. Finally, by averaging over all nodes, S quantifies the ability of an embedding to respect the neighborhood. The higher S, the more P1 is preserved.

$$\begin{aligned} S\left( v_i\right) = \dfrac{|N\left( v_i\right) \bigcap N_{E}\left( v_i\right) |}{|N\left( v_i\right) |}, S = \dfrac{1}{n}\sum _i S\left( v_i\right) \end{aligned}$$
(1)

Structural equivalence or second-order proximity (P2): two vertices are structurally equivalent if they share many of the same neighbors [13]. To measure the efficiency of an embedding method to recover the structural equivalence, we define the distance \(dist_A\left( A_{i},A_{j}\right) \) between the lines of the adjacency matrix corresponding to each pair of nodes \((v_i,v_j)\), and \(dist_E\left( Y_{i},Y_{j}\right) \) the distance between their representative vectors in the embedding space. The metric for P2 is defined by the correlation coefficient (Spearman or Pearson) \(Struct\_eq\) between those values for all pairs of nodes. The higher \(Struct\_eq\) (close to 1), the better P2 is preserved by the algorithm.

$$\begin{aligned} L_{A}\left( v_i,v_j\right) = dist_A\left( A_{i},A_{j}\right) , \,\,\, L_{E}\left( v_i,v_j\right) = dist_E\left( Y_{i},Y_{j}\right) \end{aligned}$$
(2)

with \(dist_A\) the distance in the adjacency matrix (cosine or euclidean) and \(dist_E\), the embedding similarity which is indicated in Table 1. Finally,

$$\begin{aligned} Struct\_eq = pearson(L_{A}, L_{E}) \end{aligned}$$
(3)

Isomorphic equivalence (P3): two nodes are isomorphically equivalent, i.e they share the same role in the graph, if their ego-networks are isomorphic [4]. The ego-network of node \(v_i\) is defined as the subgraph \(EN_i\) made up of its neighbors and the edges between them (without \(v_i\) itself). To go beyond a binary evaluation, for each pair of nodes \((v_i, v_j)\), we compute the Graph Edit Distance \(GED\left( EN_{i},EN_{j}\right) \) between their ego-networks \(EN_{i}\) and \(EN_{j}\) thanks to the Graph Matching Toolkit [16] and the distance between their representative vectors in the embedding space \(dist_E\left( Y_{i},Y_{j}\right) \). \(dist_E\) is indicated in Table 1. Finally, the Pearson and Spearman correlation coefficients between those values computed on all pairs of nodes are used to have an indicator for the whole graph. A negative correlation means that if the distance in the embedding space is large then exp(-GED), as in [15], is small. So, to ease one’s reading, we take the opposite of the correlation coefficient such that, for all measures, the best result is 1. Thus, the higher \(Isom\_eq\), the better P3 is preserved by the algorithm.

$$\begin{aligned} L_{Egonet}\left( v_i,v_j\right) = exp(-GED\left( EN_{i},EN_{j}\right) ), \,\, L_{E}\left( v_i,v_j\right) = dist_E\left( Y_{i},Y_{j}\right) \end{aligned}$$
(4)
$$\begin{aligned} Isom\_eq = -pearson(L_{Egonet}, L_{E}) \end{aligned}$$
(5)

Community/cluster membership (P4): communities can be defined as “groups of vertices having higher probability of being connected to each other than to members of other groups" [7]. On the other hand, clusters can be defined as sets of elements such that elements in the same cluster are more similar to each other than to those in other clusters. We propose to study the ability of an embedding method to transfer a community structure to a cluster structure. Given a graph with k ground-truth communities, we cluster, using KMeans (since k, the number of communities, is known), the node embeddings into k clusters. Finally, we compare this partition with the ground-truth partition using the adjusted mutual information (AMI). We also used the normalized mutual information (NMI) but both measures showed similar results. Let \(L_{Community}\) be the ground-truth labeling and \(L_{Clusters}\) the one found by KMeans.

$$\begin{aligned} Score = AMI(L_{Community}, L_{Clusters}) \end{aligned}$$
(6)

3 Embeddings

There are many different graph embedding algorithms. We present a non-exhaustive list of recent methods, representative of the different families proposed in the state-of-the-art. We refer the reader to the full papers for more information. In Table 1 we mention all the embedding methods we used in our comparative study with the graph similarity they are supposed to preserve and the distance that is used in the embedding space to relate any pair of nodes of the graph. Two versions of N2V are used (A: \(p=0.5, q=4\) for local random walks, B: \(p=4, q=0.5\) for deeper random walks).

Table 1. Studied methods with complexity, their graph similarity (encoder) and their distance in the embedding space (decoder)
Full size table

4 Graphs

To evaluate embedding algorithms, we choose real graphs and generated graphs having different sizes and types: random (R), with preferential attachment (PA), social (S), social with community structure (SC) as shown in Table 2. While real graphs correspond to common datasets, generators allow to control the characteristics of the graphs. Thus, we have prior knowledge which makes evaluation easier and more precise. Table 2 gives the characteristics of these graphs divided in three groups: small, medium and large graphs.

Table 2. Dataset characteristics. All graphs are provided in our GitHub
Full size table

5 Results

We used the metrics presented in Sect. 2 to quantify the ability of the embedding algorithms described in Sect. 3 to recover four properties of the graphs: first order proximity (P1), structural and isomorphic equivalences (P2 and P3), community membership (P4). Due to lack of space, we show only the most representative results and provide the others as additional materialsFootnote 1. For the same reason, to evaluate P2 and P3, both Pearson and Spearman correlation coefficients have been computed but we only show results for Pearson as they are similar with Spearman. For readability, every algorithm successfully captures a property when its corresponding score is at 1 and 0 means unsuccessful. Moreover, a dash (-) in a Table indicates that a method has not been able to provide a result. Note that due to high complexity, KKL and MDS are not computed for every graph. Finally, the code and datasets are available online on our GitHub (see footnote 1).

5.1 Neighborhood (P1)

Fig. 1.
figure 1

Neighborhood (P1) as a function of embedding dimension.

Full size image
Table 3. Neighborhood (P1) Italic: Best in row. Bold: best.
Full size table

For the first order proximity (P1), we measure the similarity S as a function of the dimension d for all the embedding methods. For computational reasons, for large graphs, the measure is computed on 10% of the nodes. Results are shown in Fig. 1 and Table 3, for d varying from 2 until approximately the number of nodes. We can make several observations: for networks with communities (Dancer and ZKC), only LE and LLE reasonably capture this property. For Barabasi Albert graph and Erdos-Renyi networks, Verse, MDS and LE reach scores higher than LLE. It means that those algorithms are able to capture this property, but are fooled by complex meso-scopic organizations. These results can be generalized as shown in additional materials. MDS can show good performance for instance on email dataset, Verse works only on our random graphs, LLE works only for ZKC and Dancer while LE seems to show good performance on every graph when the right dimension is chosen. In the cases of LE and LLE, there is an optimal dimension: the increase of the similarity as the dimension grows can be explained by the fact that enough information is learned; the decrease is due to eigen-value computation in high-dimension which is very noisy. To conclude, LE seems to be the best option to recover neighborhood but the right dimension has to be found.

5.2 Structural Equivalence (P2)

Concerning the second-order proximity (P2), we compute the Pearson correlation coefficient, as indicated in Sect. 2, as a function of the embedding space dimension d and we use the same sampling strategy as for property P1.

The results are shown in Fig. 2 and Table 4. Two methods are expected to have good results, because they explicitly embed the structural equivalence: SVD and SDNE. HOPE does not explicitly embed this property but a very similar one which is Katz-Index. On every small graph, SVD effectively performs the best and with the lowest dimension. HOPE still has very good results. The Pearson coefficient grows as the dimension of the embedding grows which implies that the best results are obtained when the dimension of the space is high enough. The other algorithms fail to recover the structural equivalence. For medium and large graphs as presented in Table 4, SVD and HOPE still show very good performance and the higher the dimension of the embedding space, the higher the correlation. For large graphs, SDNE shows also very good results but it seems to need more data to be able to learn properly. In the end, SVD seems to be the best algorithm to capture the second order proximity. It computes a singular value decomposition which is fast and scalable but SDNE performs also very well on the largest graphs and, in that case, it can outperform SVD.

Fig. 2.
figure 2

Structural equivalence (P2) as a function of embedding dimension.

Full size image

5.3 Isomorphic Equivalence (P3)

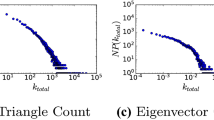
With the property P3, we investigate the ability of an embedding algorithm to capture roles in a graph. To do so, we compute the graph edit distance (GED) between every pair of nodes in the graph and the distance between the vectors of the embedding. Moreover, we sample nodes at random and compute the GED only between every pair of the sampled nodes thus reducing the computing time drastically. We sample 10% of the nodes for medium graphs and 1% of the nodes for large graphs. Experiments have demonstrated that results are robust to sampling. We present, in Fig. 3 and Table 5, the evolution of the correlation coefficient according to the dimension of the embedding space. The only algorithm that is supposed to perform well for this property is Struc2vec. Note also that algorithms which capture the structural equivalence can also give results since two nodes that are structurally equivalent are also isomorphically equivalent but the converse is not true. For small graphs, as illustrated in Fig. 3, Struc2vec (S2V) is nearly always the best. It performs well on medium and large graphs too as shown in Table 5. However results obtained on other graphs (available in supplementary material) indicate that Stru2vec is not always much better than the other algorithms. As a matter of fact, Struc2vec remains the best algorithm for this measure but it is not totally accurate since the correlation coefficient is not close to 1 on every graph e.g on Dancer10k in Table 5(b).

Table 4. Structural equivalence (P2). Italic: Best in row. Bold: best.
Full size table
Fig. 3.
figure 3

Isomorphic equivalence (P3) as a function of embedding dimension.

Full size image
Table 5. Isomorphic equivalence (P3). Italic: Best in row. Bold: best.
Full size table
Fig. 4.
figure 4

AMI for community detection on PPG (top) and Dancer (bottom)

Full size image

5.4 Community Membership (P4)

To study the ability of an embedding to recover the community structure of a graph (P4), we compare, using Adjusted Mututal Information (AMI) and Normalized (NMI), the partition given by KMeans on the node embeddings and the ground-truth partition. The results are given only for PPG (averaged over 3 instances) and Dancer graphs (for 20 different graphs) for which the community structure (ground truth) is provided by the generators. To obtain them, we generated planted partition graphs (PPG) with 10 communities and 100 nodes per community. We set the probability of an edge existing between communities \(p_{out}=0.01\) and vary the probability of an edge existing within a community \(p_{in}\) from 0.01 (no communities) to 1 (clearly defined communities), thus varying the modularity of the graph from 0 to 0.7. For Dancer, we generate 20 graphs with varying community structure by adding between-community edges and removing within-community edges. Moreover, we apply also usual community detection algorithms such as Louvain’s modularity maximisation (maxmod) [2] and Infomap [3] on the graphs. Results are shown in Fig. 4. In low dimension (d = 2, left of the Figure), every embedding is less efficient than the usual community detection algorithms. In higher dimension (d = 128, right of the Figure), many embedding techniques, Verse, MDS, N2V (both versions) and HOPE (on PPG), are able to have the same results as the best community detection algorithm: Louvain and obvioulsly for all the methods, AMI increases with the modularity.

6 Conclusion

In this paper, we studied how a wide range of graph embedding techniques preserve essential structural properties of graphs. Most of recent works on graph embeddings focused on the introduction of new methods and on task-oriented evaluation but they ignore the rationale of the methods, and only focus on their performance on a specific task in a particular setting. As a consequence, methods that have been designed to embed local structures are compared with methods that should embed global structures on tasks as diverse as link prediction or community detection. In contrast, we focused on (i) The structural properties for which each algorithm has been designed, and (ii) How well these properties are effectively preserved in practice, on networks having diverse topological properties. As a result, we have shown that no method embed efficiently all properties, and that most methods embed effectively only one of them. We have also shown that most of recently introduced methods are outperformed or at least challenged by older methods specifically designed for that purpose, such as LE/LLE for P1, SVD for P2, and modularity optimization for P4. Finally, we have shown that, even when they have been designed to embed a particular property, most methods fail to do so in every setting. In particular, some algorithms (particularly LE and LLE) have shown an important, non-monotonous sensibility to the number of dimensions which can be difficult to choose in a non supervised context.

In order to improve graph embedding methods, we believe that we need to better understand the nature of produced embeddings. We wish to pursue this work in two directions, (1) Understanding how those methods can obtain good results on tasks depending mainly on local structures, such as link prediction, when they do not encode efficiently local properties, and (2) study how well the meso-scale structure is preserved by such algorithms.