Abstract
We present a detailed overview of the construction of the \(\mathbb A_{{\mathrm {inf}}}\)-cohomology theory from the preprint Integral p-adic Hodge theory, joint with Bhatt and Scholze. We focus particularly on the p-adic analogue of the Cartier isomorphism via relative de Rham–Witt complexes.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
To be precise, there is one step in the construction, namely the equality (dim\(_\mathfrak X\)) in the proof of Theorem 7, where we will have to assume that the p-adic scheme \(\mathfrak X\) is defined over a discretely valued field; this assumption can be overcome using the crystalline comparison theorems of [5].
- 2.
To be precise, the isomorphism depends only on a choice of specialisation of geometric points of \({{\,\mathrm{Spec}\,}}\mathcal {O}_K\). A consequence of the compatibility with Galois actions is that the action of \(G_K\) on \(H^i_ {\acute{\mathrm {e}}{\mathrm {t}}}(\mathfrak X_{\overline{K}},\mathbb Z_\ell )\) is unramified.
- 3.
Our results can presumably make this more precise.
- 4.
In [5, Theorem 2.10] we also give an example for which \(H^2_ {\acute{\mathrm {e}}{\mathrm {t}}}(\mathfrak X_{\overline{K}})_{{\mathrm {tors}}}=\mathbb Z/p^2\mathbb Z\) and \(H^2_{{\mathrm {crys}}}(\mathfrak X_k)_{{\mathrm {tors}}}=k\oplus k\).
- 5.
More general, most of the theory which we will present works for any perfectoid field of mixed characteristic which contains all p-power roots of unity.
- 6.
A brief introduction to \(\mathcal {O}^\flat \) and \(\mathbb A_{{\mathrm {inf}}}\) may be found at the beginning of Appendix 1.
- 7.
Throughout these notes we follow the convention that formally smooth/étale includes the condition of being topologically finitely presented, i.e., a quotient of \(\mathcal {O}\langle T_1,\ldots ,T_N \rangle \) by a finitely generated ideal. Under this convention formal smoothness implies flatness. In fact, according to a result of Elkik [11, Theorem 7] (see Rmq. 2 on p. 587 for elimination of the Noetherian hypothesis), a p-adically complete \(\mathcal {O}\)-algebra is formally smooth if and only if it is the p-adic completion of a smooth \(\mathcal {O}\)-algebra.
- 8.
In this footnote we carry out the calculation of the proof of Theorem 2 when \(R=\mathcal {O}\langle T^{\pm 1} \rangle \), in which case \(R_\infty =\mathcal {O}\langle T^{\pm 1/p^\infty } \rangle \). To reiterate, we must show that \(H^i_{{\mathrm {cont}}}(\varGamma ,R_\infty )\) is good for all \(i\ge 0\).
First note that \(R_\infty \) admits a \(\varGamma \)-equivariant decomposition into \(\mathcal {O}\)-submodules
$$\begin{aligned} R_\infty =\widehat{\bigoplus }_{k\in \mathbb Z\left[ \tfrac{1}{p}\right] }\mathcal {O}T^k \end{aligned}$$(where the hat denotes p-adic completion of the sum), with the generator \(\gamma \in \varGamma \) acting on the rank-one free \(\mathcal {O}\)-module \(\mathcal {O}T^k\) as multiplication by \(\zeta ^k\). Thus \(R\varGamma _{{\mathrm {cont}}}(\mathbb Z_p,\mathcal {O}T^k)\simeq [\mathcal {O}\xrightarrow {\zeta ^k-1}\mathcal {O}]\) (since the group cohomology of an infinite cyclic group with generator \(\gamma \) is computed by the invariants and coinvariants of \(\gamma \), and similarly in the case of continuous group cohomology), and so
$$\begin{aligned} R\varGamma _{\mathrm {cont}}(\mathbb Z_p,R_\infty )\simeq \widehat{\bigoplus }_{k\in \mathbb Z\left[ \tfrac{1}{p}\right] }[\mathcal {O}\xrightarrow {\zeta ^k-1}\mathcal {O}] \end{aligned}$$(where the hat now denotes the derived p-adic completion of the sum of complexes), which has cohomology groups
$$\begin{aligned} H^0_{{\mathrm {cont}}}(\mathbb Z_p,R_\infty )\cong \widehat{\bigoplus }_{k\in \mathbb Z}\mathcal {O}\oplus 0,\qquad H^1_{{\mathrm {cont}}}(\mathbb Z_p,R_\infty )\cong \widehat{\bigoplus }_{k\in \mathbb Z}\mathcal {O}\oplus \bigoplus _{k\in \mathbb Z\left[ \tfrac{1}{p}\right] \setminus \mathbb Z}\mathcal {O}/(\zeta ^k-1)\mathcal {O}\end{aligned}$$(once some care is taken regarding the p-adic completions: see footnote 9).
We claim that both cohomology groups are good. Since \(\mathcal {O}\) has no non-zero elements killed by \(\mathfrak m\), it remains only to prove that the same is true of \(\mathcal {O}/a\mathcal {O}\), where \(a=f\) or \(\zeta ^k-1\) for some \(k\in \mathbb Z[\tfrac{1}{p}]\setminus \mathbb Z\). But this is an easy argument with valuations: if \(x\in \mathcal {O}\) is almost a multiple of a, then \(\nu _p(x)+\varepsilon \ge \nu _p(a)\) for all \(\varepsilon >0\), whence \(\nu _p(x)\ge \nu _p(a)\) and so x is actually a multiple of a.
- 9.
This step requires some care about p-adic completions: the following straightforward result is sufficient. Suppose \((C_\lambda )_\lambda \) is a family of complexes satisfying the following for all \(i\in \mathbb Z\): the group \(H^i(C_\lambda )\) is p-adically complete and separated for all \(\lambda \), with a bound on its p-power-torsion which is independent of \(\lambda \). Then \(H^i(\widehat{\bigoplus }_\lambda C_\lambda )=\widehat{\bigoplus }_\lambda H^i(C_\lambda )\), where the left hat is the derived p-adic completion of the sum of complexes, and the right hat is the usual p-adic completion of the sum of cohomology groups. Proof. Set \(C_{{\mathrm {disc}}}:=\bigoplus _\lambda C_\lambda \) and \(C=\widehat{C_{{\mathrm {disc}}}}\) (derived p-adic completion); then the usual short exact sequences associated to a derived p-adic completion are
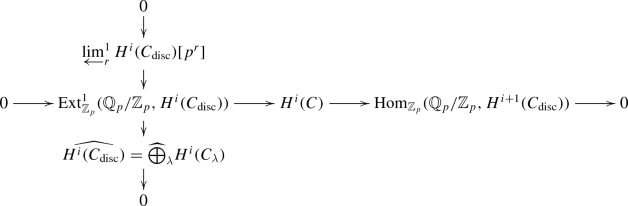
Our assumption that \(\bigoplus _\lambda H^i(C_\lambda )\) has bounded p-power-torsion implies that the right and top terms vanish.
- 10.
In all our cases of interest the ring A will be an integral domain, in which case it may be psychologically comforting to note that \(A^\flat \) and \(W(A^\flat )\) are also integral domains. Proof. The ring \(W(A^\flat )\) is p-adically separated, satisfies \(W(A^\flat )/p=A^\flat \), and p is a non-zero-divisor in it (these properties all follow simply from \(A^\flat \) being perfect). So, once we show that \(A^\flat \) is an integral domain, it will easily follow that \(W(A^\flat )\) is also an integral domain. But the fact that \(A^\flat \) is an integral domain follows at once from the same property of A using the isomorphism of monoids \(\varprojlim _{x\mapsto x^p}A{\mathop {\rightarrow }\limits ^{\simeq }}A^\flat \) which already appeared in Lemma 4.
- 11.
Perhaps “integral perfectoid ring” would be better terminology to avoid conflict with the more common notion of perfectoid algebras in which p is invertible.
- 12.
There is an equivalence of categories between quasi-separated rigid analytic varieties over \(\mathbb C\) and those adic spaces over \({{\,\mathrm{Spa}\,}}(\mathbb C,\mathcal {O})\) whose structure map is quasi-separated and locally of finite-type [16, Proposition 4.5]. A collection of étale maps \(\{f_\lambda :U_\lambda \rightarrow U\}\) in \(X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) is a cover if and only if it is jointly “strongly surjective”, which is equivalent to being jointly surjective at the level of adic points [17, Sect. 2.1].
- 13.
This means that we are permitted to replace the towers
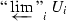 and
and  by “obviously isomorphic” towers, e.g., by inserting or removing some stages of the tower. To be precise, first let \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) denote the usual category of countable inverse systems in \(X_ {\acute{\mathrm {e}}{\mathrm {t}}}\): its objects are inverse systems
by “obviously isomorphic” towers, e.g., by inserting or removing some stages of the tower. To be precise, first let \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) denote the usual category of countable inverse systems in \(X_ {\acute{\mathrm {e}}{\mathrm {t}}}\): its objects are inverse systems 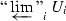 in \(X_ {\acute{\mathrm {e}}{\mathrm {t}}}\), and its morphisms are defined by
in \(X_ {\acute{\mathrm {e}}{\mathrm {t}}}\), and its morphisms are defined by 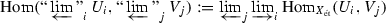 . Then call an object \(\mathcal U\) of \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) pro-étale if and only if it is isomorphic in \({\text {pro-}}~X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) to an inverse system
. Then call an object \(\mathcal U\) of \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) pro-étale if and only if it is isomorphic in \({\text {pro-}}~X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) to an inverse system 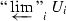 whose transition maps are finite étale surjective; and call a morphism \(f:\mathcal U\rightarrow \mathcal V\) pro-étale if and only if there exist isomorphisms
whose transition maps are finite étale surjective; and call a morphism \(f:\mathcal U\rightarrow \mathcal V\) pro-étale if and only if there exist isomorphisms 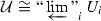 and
and 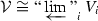 in \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) such that
in \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) such that  and
and 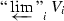 have finite étale surjective transition maps and such that the resulting morphism
have finite étale surjective transition maps and such that the resulting morphism 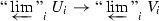 has the shape described in the main text. Then the category \(X_{{\mathrm {pro}}\acute{\mathrm {e}}{\mathrm {t}}}\) is more correctly defined as the full subcategory of \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) consisting of pro-étale objects, and covers are defined as in the main text using the more correct definition of a pro-étale morphism.
has the shape described in the main text. Then the category \(X_{{\mathrm {pro}}\acute{\mathrm {e}}{\mathrm {t}}}\) is more correctly defined as the full subcategory of \({\text {pro-}}X_ {\acute{\mathrm {e}}{\mathrm {t}}}\) consisting of pro-étale objects, and covers are defined as in the main text using the more correct definition of a pro-étale morphism. - 14.
The topos of abelian sheaves on \(X_{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}\) is “algebraic” in the sense of [27, Definition VI.2.3]; see [25, Proposition 3.12] for this and further properties of the site. In particular, it then follows from [27, Corollary VI.5.3] that if \(\mathcal U\in X_{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}\) is such that \(|\mathcal U|\) is quasi-compact and quasi-separated, then \(H^*_{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(\mathcal U,-)\) commutes with filtered inductive colimits of sheaves.
- 15.
Nonetheless, a condition is required: we must assume that the topological space \(|\mathcal U|\) is quasi-compact and quasi-separated; this is satisfied in particular when \(\mathcal U\) is a tower of rigid affinoids.
- 16.
Unlike the rational structure sheaf, the integral structure sheaf can have non-zero higher cohomology on rigid affinoids.
- 17.
We emphasise that, in our current set-up, this perfectoid ring will always be the type considered in Sect. 3.3: indeed, it is p-torsion-free since each \(T_i\) is p-torsion-free, and it contains a compatible sequence of primitive p-power roots of unity since it contains \(\mathcal {O}\).
- 18.
Usually denoted by \(\widehat{\mathcal {O}}_{X^\flat }^+\) to evoke the idea of it being the completed integral structure sheaf on the tilt \(X^\flat \) of X.
- 19.
If \(\mathcal R\) is a sheaf of rings on a site \(\mathcal T\), then \(W_r(\mathcal R)\) and \(W(\mathcal R)\) are the sheaves of rings obtained by applying the Witt vector construction section-wise, i.e., \(W_r(\mathcal R)(U):=W_r(\mathcal R(U))\) and \(W(\mathcal R)(U):=W(\mathcal R(U))\) for all \(U\in \mathcal T\).
- 20.
Now seems to be an appropriate moment for mentioning some formalism of almost mathematics over Witt rings. By a “setting for almost mathematics” we mean a pair (V, I), where V is a ring and \(I=I^2\subseteq V\) is an ideal which is an increasing union of principal ideals \(\bigcup _\lambda t_\lambda V\) generated by non-zero-divisors \(t_\lambda \). Elementary manipulations of Witt vectors [5, Lemma 10.1 and Corollary 10.2] then show that each Teichmüller lift \([t_\lambda ]\in W_r(V)\) is a non-zero-divisor and that \(W_r(I):={\text {Ker}}(W_r(V)\rightarrow W_r(V/I))\) equals the increasing union \(\bigcup _\lambda [t_\lambda ]W_r(V)\), which moreover coincides with its square; in conclusion, the pair \((W_r(V), W_r(I))\) is also a setting for almost mathematics. We apply this above, and elsewhere, in the cases \((V,I)=(\mathcal {O},\mathfrak m)\) and \((\mathcal {O}^\flat ,\mathfrak m^\flat )\).
Upon taking the limit as \(r\rightarrow \infty \), the inclusion \(W(I):={\text {Ker}}(W(V)\rightarrow W(V/I))\supset [I]:=\bigcup _\lambda [t_\lambda ]W(V)\) is strict; the pair (W(V), [I]) is a setting for almost mathematics, but (W(V), W(I)) typically is not. So, strictly, speaking, the almost language should be avoided for the ideal \(W(\mathfrak m^\flat )\), though we will sometimes abuse this. However, if V is a perfect ring of characteristic p (e.g., \(V=\mathcal {O}^\flat \)), then [I] and W(I) coincide after p-adic completion (and derived p-adic completion) by the argument of the proof of Lemma 22; so a map between p-adically complete W(V)-modules (resp. derived p-adically complete complexes of W(V)-modules) has kernel and cokernel (resp. all cohomology groups of the cone) killed by W(I) if and only if they are killed by [I].
- 21.
Often called Hochschild–Serre in this setting. Here \(H^*_{{\mathrm {grp}}}\) and \(R\varGamma _{{\mathrm {grp}}}\) refer to group cohomology for a topological group acting on discrete modules.
- 22.
This process of taking the inverse limit deserves further explanation. By definition, when G is a topological group and M is a complete topological G-module whose topology is defined by a system \(\{N\}\) of open sub-G-submodules, we define its continuous group cohomology as \(R\varGamma _{{\mathrm {cont}}}(G,M):=R\!{\text {lim}}_NR\varGamma _{{\mathrm {grp}}}(G,M/N)\) and \(H^*_{{\mathrm {cont}}}(G,M):=H^*(R\varGamma _{{\mathrm {cont}}}(G,M))\); of course, we may always restrict the limit to any preferred system of open neighbourhoods of 0 by sub-G-modules. In particular, \(R\varGamma _{{\mathrm {cont}}}(\mathbb Z_p(1)^d,R_\infty )=R\!{\text {lim}}_sR\varGamma _{{\mathrm {grp}}}(\mathbb Z_p(1)^d,R_\infty /p^sR_\infty )\).
To take the inverse limit of the right, we show that the canonical map \(R\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(U,\widehat{\mathcal {O}}_X^+)\rightarrow R\!{\text {lim}}_sR\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(U,\mathcal {O}_X^+/p^s)\) is a quasi-isomorphism. Since the codomain may be rewritten as \(R\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(U,R\!{\text {lim}}_s\mathcal {O}_X^+/p^s)\) by general formalism of derived functors, it is enough to show that the canonical map \(\widehat{\mathcal {O}}_X^+\rightarrow R\!{\text {lim}}_s\mathcal {O}_X^+/p^s\) is a quasi-isomorphism (note that the topos of pro-étale sheaves does not satisfy the necessary Grothendieck axioms to automatically imply that higher derived inverse limits vanish in the case of surjective transition maps!), for which it is enough to show that \(R\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(\mathcal V,\widehat{\mathcal {O}}_X^+)\rightarrow R\!{\text {lim}}_sR\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(\mathcal V,\mathcal {O}_X^+/p^s)\) is a quasi-isomorphism for every affinoid perfectoid \(\mathcal V\in X_{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}\); this is what we shall now do. Firstly, it is easily seen to be an almost quasi-isomorphism by Lemma 11, and so in particular the cone is derived p-adically complete; since the codomain is derived p-adically complete, therefore the domain is also; but the codomain is precisely the derived p-adic completion of the domain, and hence the map is a quasi-isomorphism.
Unfortunately the same argument does not work for the sheaf \(\mathbb A_{{\mathrm {inf}},X}\), which seemingly fails to be derived p-adically complete on \(X_{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}\); in particular, the canonical map \(R\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(U,\mathbb A_{{\mathrm {inf}},X})\rightarrow R\!{\text {lim}}_sR\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}(U,\mathbb A_{{\mathrm {inf}},X}/p^s)\) is only a quasi-isomorphism after replacing the domain by its derived p-adic completion.
- 23.
- 24.
This is not automatic from the first condition since C may be unbounded, and is a standard condition to impose when requiring flatness conditions on unbounded complexes of sheaves.
- 25.
For example, given a proper smooth variety Y over k, Proposition 1 provides a quasi-isomorphism \(W\varOmega ^\bullet _{Y/k}{\mathop {\rightarrow }\limits ^{\sim }}L\eta _pW\varOmega ^\bullet _{Y/k}\) of sheaves; if the global-to-local comparison morphism were an isomorphism, we would deduce that \(R\varGamma _{{\mathrm {crys}}}(Y/W(k)){\mathop {\rightarrow }\limits ^{\sim }}L\eta _pR\varGamma _{{\mathrm {crys}}}(Y/W(k))\), whence \(H^n_{{\mathrm {crys}}}(Y/W(k)){\mathop {\rightarrow }\limits ^{\simeq }}H^i_{{\mathrm {crys}}}(Y/W(k))/H^i_{{\mathrm {crys}}}(Y/W(k))[p]\) for all \(i\ge 0\) by Lemma 1. But the p-power torsion in \(H^i_{{\mathrm {crys}}}(Y/W(k))\) is bounded since it is a finitely generated W(k)-module, so the previous isomorphism would in fact force \(H^i_{{\mathrm {crys}}}(Y/W(k))\) to be p-torsion-free for all \(i\ge 0\); but this is well-known to be false, e.g., when Y is an Enriques surface in characteristic two and \(i=2\) or 3 [18, Proposition II.7.3.5].
- 26.
The astute reader may notice that in this argument we have just implicitly identified \(L\eta _\mu \big (\widehat{R\varGamma _{{\mathrm {pro}}{\acute{\mathrm {e}}}{\mathrm {t}}}({{\,\mathrm{Sp}\,}}R[\tfrac{1}{p}],\mathbb A_{{\mathrm {inf}},X})}\big )\) and \(R\varGamma _{{\mathrm {Zar}}}({{\,\mathrm{Spf}\,}}R,\mathbb A\varOmega _{\mathfrak X})\), contrary to the warning of Remark 4; this is precisely the type of technical obstacle which will need to be overcome in Sect. 7.1.
- 27.
In the case \(r=1\), the accepted terminology is now “Hodge–Tate comparison”.
- 28.
As written, this isomorphism is natural but not canonical: it depends on the chosen sequence of p-power roots of unity. To make it independent of any choices, the right side should be replaced by \(\mathcal H^i(\widetilde{W_r\varOmega }_{\mathfrak X/\mathcal {O}})\otimes _{W_r(\mathcal {O})}({\text {Ker}}\,\widetilde{\theta }_r/({\text {Ker}}\,\widetilde{\theta }_r)^2)^{\otimes i}\). Here \({\text {Ker}}\,\widetilde{\theta }_r/({\text {Ker}}\,\widetilde{\theta }_r)^2=\widetilde{\xi }_r\mathbb A_{{\mathrm {inf}}}/\widetilde{\xi }_r^2\mathbb A_{{\mathrm {inf}}}\) is a certain canonical rank-one free \(W_r(\mathcal {O})\)-module, and so we are replacing the right side by a type of Tate twist \(\mathcal H^i(\widetilde{W_r\varOmega }_{\mathfrak X/\mathcal {O}})\{i\}\). This dependence arrises as follows: changing the chosen sequence of p-power roots of unity changes \(\mu \) up to a unit in \(\mathbb A_{{\mathrm {inf}}}\): this does not affect \(L\eta _\mu \) (which depends only on the ideal generated by \(\mu \)), but does affect the forthcoming isomorphism in Remark 7(a) (see footnote 29).
- 29.
Continuing the theme of the previous footnote, the left side depends only on the ideal fA while the right side currently depends on the chosen generator f; to make the construction and morphism independent of this choice, each cohomology group on the right should be replaced by the twist \(H^*(D\otimes ^{\mathbb {L}}_AA/fA)\otimes _{A/fA}(f^*A/f^{*+1}A)\).
- 30.
Curiously, this shows that the complex \((L\eta _f D)\otimes ^{\mathbb {L}}_AA/fA\), which a priori lives only in the derived category of A/fA-modules, has a natural representative by an actual complex.
- 31.
Proof. \(\mathcal H^0(C)=\nu _*\mathbb A_{{\mathrm {inf}},X}\) has no \(\mu \)-torsion since \(\mathbb A_{{\mathrm {inf}},X}\) has no \(\mu \)-torsion by Corollary 3; thus \(\mathcal H^0(L\eta _\mu C){\mathop {\rightarrow }\limits ^{\simeq }}\mathcal H^0(C)\) by Remark 7(d). But since \(\mathcal H^0(C)\) has no \(\mu \)-torsion, it also has no \(\varphi (\mu )=\widetilde{\xi }\mu \)-torsion, thus has no \(\widetilde{\xi }\)-torsion.
- 32.
“Proof”. If f, g are non-zero-divisors of a ring A, and D is complex of A-modules which is derived g-adically complete, then we claim that \(L\eta _fD\) is still derived g-adically complete: indeed, this follows from the fact that a complex is derived g-adically complete if and only if all of its cohomology groups are derived g-adically complete, that \(H^i(L\eta _f D)\cong H^i(D)/H^i(D)[f]\) for all \(i\in \mathbb Z\) by Lemma 1, and that kernels and cokernels of maps between derived g-adically complete modules are again derived g-adically complete. For a reference on such matters, see The Stacks Project, Tag 091N.
It is tempting to claim that the previous paragraph remains valid for the complex of sheaves \(\widehat{R\nu _*\mathbb A_{{\mathrm {inf}},X}}\) (which is indeed derived \(\xi \)-adically complete, since \(R\nu _*\) and derived p-adic completion preserve the derived \(\xi \)-adic completeness of the pro-étale sheaf \(\mathbb A_{{\mathrm {inf}},X}\)), which would complete the proof since \(R\varGamma _{{\mathrm {Zar}}}(\mathfrak X,-)\) also preserves derived \(\xi \)-adic completeness, but unfortunately the previous paragraph does not remain valid for complexes of sheaves on a “non-replete” site (e.g., the Zariski site). In fact, it seems that the derived \(\xi \)-adic completeness of \(R\varGamma _\mathbb A(\mathfrak X)\) is not purely formal, and requires the technical lemmas established in Sect. 7.1; therefore we have postponed a proof of the completeness to Corollary 4.
- 33.
Proof. By derived p-adically completeness, it is enough to check that \(R\varGamma _{{\mathrm {dR}}}(\mathfrak X/\mathcal {O})\otimes ^{\mathbb {L}}_{\mathcal {O}}\mathcal {O}/p\mathcal {O}=R\varGamma _{{\mathrm {dR}}}(\mathfrak X\otimes _{\mathcal {O}}\mathcal {O}/p\mathcal {O}/(\mathcal {O}/p\mathcal {O}))\) is a perfect complex of \(\mathcal {O}/p\mathcal {O}\)-modules; this follows from the facts that \(\varOmega _{\mathfrak X\otimes _{\mathcal {O}}\mathcal {O}/p\mathcal {O}/(\mathcal {O}/p\mathcal {O})}^\bullet \) is a perfect complex of \(\mathcal {O}_{\mathfrak X\otimes _{\mathcal {O}}\mathcal {O}/p\mathcal {O}}\)-modules by smoothness, and that the structure map \(\mathfrak X\otimes _{\mathcal {O}}\mathcal {O}/p\mathcal {O}\rightarrow {{\,\mathrm{Spec}\,}}\mathcal {O}/p\mathcal {O}\) is proper, flat, and of finite presentation.
- 34.
Possibly (dim\(_\mathfrak X\)) can be proved in this case by combining spreading-out arguments of Conrad–Gabber with the relative p-adic Hodge theory of [25, Sect. 8], but the author has not seriously considered the problem.
- 35.
The Teichmüller identity follows from the other axioms if \(\mathcal W_r^1\) is p-torsion-free:
$$\begin{aligned}&p\lambda _r([b])^{p-1}d\lambda _r([b])=d\lambda _r([b]^p)=dF\lambda _r([b])=FdVF\lambda _r([b])\\ {}&=Fd(\lambda _r([b])V(1))=F(V(1))d\lambda _r([b])=pFd\lambda _r([b]).\end{aligned}$$ - 36.
For the elementary proof that the three completions are the same, see Lemma 10.3 and Corollary 10.10 of [5].
- 37.
By this we mean that D is a commutative algebra object in the category \(D(W(A^\flat ))\) in the most naive way: the constructions can be upgraded to the level of \(\mathbb E_\infty \)-algebras, but again this is not necessary for our existing results.
- 38.
From assumption (\(\mathcal W1\)) and the existence of \(\varphi _D\), it follows that \(H^0(D)\) has no \(\varphi ^r(\mu )=\widetilde{\xi }_r\mu \)-torsion, hence no \(\widetilde{\xi }_r\)-torsion; so \(D/\widetilde{\xi }_r\) is still coconnective.
- 39.
The reader should use the identities of Sect. 3.3 to calculate that \(\widetilde{\theta }_r(\xi )=\tfrac{[\zeta _{p^r}]-1}{[\zeta _{p^{r+1}}]-1}\in W_r(A)\).
- 40.
Unfortunately this is not strictly true: if \(p=2\) then the condition that \(x^2=0\) for \(x\in \mathcal W_r^{\mathrm {odd}}(D)_{{\mathrm {pre}}}\) need not be true; but this will be fixed when we improve the construction.
- 41.
For example, suppose that B is an A-algebra and that we are given structure maps \(\lambda _r:W_r(B)\rightarrow \mathcal W_r^0(D)\) under which \((\mathcal W_r^\bullet (D),R,F,V,\lambda _r)\) becomes a Witt complex for \(A\rightarrow B\), thereby resulting in a universal map of Witt complexes \(\lambda _r^\bullet :W_r\varOmega _{B/A}^\bullet \rightarrow W_r^\bullet (D)\); then from the surjectivity of the restriction maps for \(W_r\varOmega ^\bullet _{B/A}\) and the definition of the restriction map R for \(\mathcal W_r^\bullet (D)_{{\mathrm {pre}}}\), we see that
$$ {\text {Im}}\lambda _r^n\subseteq \bigcap _{s\ge 1}{\text {Im}}(\mathcal W_{r+s}^n(D)_{{\mathrm {pre}}}\xrightarrow {R^s}\mathcal W_r^n(D)_{{\mathrm {pre}}})\subseteq \bigcap _{s\ge 1}\widetilde{\theta }_r(\xi _s)^n\mathcal W_r^n(D)_{{\mathrm {pre}}}=\bigcap _{s\ge 1}\left( \tfrac{[\zeta _{p^r}]-1}{[\zeta _{p^s}]-1}\right) ^n\mathcal W_r^n(D)_{{\mathrm {pre}}}. $$The far right side contains, and often equals in realistic situations, \(([\zeta _{p^r}]-1)^n\mathcal W_r^n(D)_{{\mathrm {pre}}}\), which motivates our replacement.
- 42.
On the other hand, if \(C\in D(S)\) then the canonical restriction map \(L\eta _f(C|_A)\rightarrow L\eta _{\alpha (f)}(C)|_D\) in D(A), which the reader will also easily construct, is always a quasi-isomorphism.
- 43.
This was erroneously asserted to be true in the official announcement without the g-torsion-freeness assumption.
- 44.
Note in particular that (\(\mathcal W3\)) is satisfied if the cohomology groups of \(D\otimes ^{\mathbb {L}}_{W(A^\flat )}W(A^\flat )/\mu \) are p-torsion-free; this follows from Remark 9(ii) since \(\widetilde{\xi }_r\equiv p^r\) mod \(\mu W(A^\flat )\).
- 45.
\(2x^2=0\) so \(x^2=0\), c.f., footnote 40. For the Teichmüller identity see footnote 35.
- 46.
Proof. We will show that \(\varepsilon ^k-1\) is a non-zero-divisor of \(A^\flat \). If \(x\in A^\flat =\varprojlim _{x\mapsto x^p}A\) satisfies \(\varepsilon ^kx=x\), then \(\zeta ^{k/p^i}x^{(i)}=x^{(i)}\) for all \(i\ge 0\), and so \(x^{(i)}=0\) for \(i\gg 0\) since then \(\zeta ^{k/p^i}-1\) is a non-zero-divisor of A, just as at the end of the proof of Proposition 2.
- 47.
This isomorphism is proved by localising the analogous assertion for \(A[\underline{T}^{1/p^\infty }]\), which is an easy consequence of [22, Corollary 2.4]. The cited result also implies that \(W_r(A[\underline{T}^{\pm 1}])\) is generated as a \(W_r(A)\)-module by the elements \(V^j([T_i^k])\), for \(k\in \mathbb Z\), \(j\ge 0\), \(i=1,\ldots ,d\), which proves the uniqueness of the maps \(\lambda _{r,{\mathrm {grp}}}\).
- 48.
To then deduce that \(\lambda _{r,{\mathrm {grp}}}^n\) itself is an isomorphism, one applies a form of Nakayama’s lemma exploiting the fact that (the non-finitely generated \(W_r(A)\)-modules) \(W_r\varOmega ^n_{A[\underline{T}^{\pm 1}]/A}\) and \(\mathcal W_r^n(D^{\mathrm {grp}})\) admit compatible direct sum decompositions into certain finitely generated \(W_r(A)\)-modules for which Nakayama’s lemma is valid; see [5, Lemma 11.14] for the details.
- 49.
The complex \(D^{\mathrm {grp}}_{{\mathrm {int}}}\) (resp. \(D_{{\mathrm {int}},i}^{\mathrm {grp}}\)) is in fact the “q-de Rham complex” \([\varepsilon ]\text{- }\varOmega ^\bullet _{W(A^\flat )[\underline{U}^{\pm 1}]/W(A^\flat )}\) (resp. \([\varepsilon ]\text{- }\varOmega ^\bullet _{W(A^\flat )[U_i^{\pm 1}]/W(A^\flat )}\)) of \(W(A^\flat )[\underline{U}^{\pm 1}]\) (resp. \(W(A^\flat )[U_i^{\pm 1}]\)) associated to the element \(q=[\varepsilon ]\in W(A^\flat )\).
- 50.
If \(\alpha :R\rightarrow S\) is a ring homomorphism, \(f\in R\) is a non-zero-divisor whose image \(\alpha (f)\in S\) is still a non-zero-divisor, and \(C\in D(R)\), then there is a base change map \([H^\bullet (C\otimes ^{\mathbb {L}}_RR/fR),{\text {Bock}}_f]\otimes _{R/fR}S/\alpha (f)S\rightarrow [H^\bullet (C\otimes ^{\mathbb {L}}_RS/\alpha (f)S),{\text {Bock}}_{\alpha (f)}]\) of complexes of \(S/\alpha (f)S\)-modules; it is an isomorphism if the R/fR-modules \(H^*(D\otimes ^{\mathbb {L}}_RR/fR)\) are Tor-independent from \(S/\alpha (f)S\), as the reader will easily prove (c.f., Remark 9(ii)).
Here we are applying this base change along the canonical map \(W(A^\flat )\rightarrow W(\kappa )\), which sends \(\widetilde{\xi }_r\) to \(p^r\), and the complex \(\eta _fD_{{\mathrm {grp}}}\). The Tor-independence condition is satisfied in this case since the \(W_r(A)\)-modules \(\mathcal W_r^*(D_{{\mathrm {grp}}})\) are Tor-independent from \(W_r(k)\): indeed, the proof of Lemma 15 shows that the cohomology groups of \(\eta _\mu D_{{\mathrm {grp}}}/\widetilde{\xi }_r\) are direct sums of \(W_r(A)\)-modules of the form
$$\begin{aligned} W_r(A), \qquad W_r(A)\left[ \tfrac{[\zeta _{p^j}]-1}{[\zeta _{p^r}]-1}\right] ,\qquad \text {and}\qquad W_r(A)/\tfrac{[\zeta _{p^{j}}]-1}{[\zeta _{p^r}]-1}, \qquad 1\le j<r, \end{aligned}$$which are Tor-independent from \(W_r(\kappa )\) by Lemmas 3.13 and 3.18(iii) and Remark 3.19 of [5].
- 51.
Here we explain why the analogous calculations we have already seen do not generalise to this case. Although there is an identification \(\mathbb A_{{\mathrm {inf}}}\langle \underline{U}^{\pm 1/p^\infty }\rangle {\mathop {\rightarrow }\limits ^{\simeq }}W(\mathcal {O}\langle \underline{T}^{\pm 1/p^\infty } \rangle ^\flat )\), the convergence of the power series on the left is with respect to the \(\langle p,\xi \rangle \)-adic topology. But neither \(R\varGamma _{{\mathrm {cont}}}(\mathbb Z_p(1)^d,\cdot )\) nor \(L\eta _\mu \) commute with derived \(\langle p,\xi \rangle \)-adic completion!
- 52.
If A is any perfectoid ring then \(W(A^\flat )\) is \({\text {Ker}}\,\theta \)-adically complete.
- 53.
Here we are of course using the trivial identification \(\widetilde{W_r\varOmega }_{\mathfrak X/\mathcal {O}}|_{{{\,\mathrm{Spf}\,}}R}=\widetilde{W_r\varOmega }_{{{\,\mathrm{Spf}\,}}R/\mathcal {O}}\) in order to appeal to the affine results in Sect. 7.1.
- 54.
This map is injective and identifies the right with the \(\langle p,\xi \rangle \)-adic completion of the left, i.e., with \(\mathbb A_{{\mathrm {inf}}}\langle \underline{U}^{\pm 1/p^\infty }\rangle \), but we do not need this.
- 55.
By Remark 8(vi), the p-adic completions may be identified respectively with \(\varprojlim _sW_r\varOmega ^n_{(\mathcal {O}[\underline{T}^{\pm 1}]/p^s)/(\mathcal {O}/p^s\mathcal {O})}\) and \(\varprojlim _sW_r\varOmega ^n_{(\mathcal {O}\langle \underline{T}^{\pm 1} \rangle /p^s)/(\mathcal {O}/p^s\mathcal {O})}\), which are clearly the same.
- 56.
We sketch the proof here, which is obtained by reversing the roles of \(\mathcal {O}\) and \(\mathcal {O}^\flat \) in [24, Proposition 3.8]. Let \(p^\flat :=(p,p^{1/p},p^{1/p^2},\ldots )\in A^\flat \), whose absolute value \(|p^\flat |=|p|\) we may normalise to \(p^{-1}\) for simplicity of notation. It is sufficient to prove the following, which allows a root to any given polynomial to be built by successive approximation: If \(f(X)\in \mathcal {O}^\flat [X]\) is a monic irreducible polynomial of degree \(d\ge 1\), and \(\alpha \in \mathcal {O}^\flat \) satisfies \(|f(\alpha )|\le p^{-n}\) for some \(n\ge 0\), then there exists \(\varepsilon \in \mathcal {O}\) satisfying \(|\varepsilon |\le p^{-n/d}\) and \(|f(\alpha +\varepsilon )|\le p^{-(n+1)}\). Well, given such f(X) and \(\alpha \), use the fact that \(\mathbb C^\flat \) and \(\mathbb C\) have the same value group (this is easy to prove), which is divisible since \(\mathbb C\) is algebraically closed, to find \(c\in \mathcal {O}^\flat \) such that \(c^{-d}f(\alpha )\) is a unit of \(\mathcal {O}^\flat \). Then \(g(X):=c^{-d}f(\alpha +cX)\) is a monic irreducible polynomial in \(\mathbb C^\flat [X]\) whose constant coefficient lies in \(\mathcal {O}^\flat \) (even \(\mathcal {O}^{\flat \times }\)); a standard consequence of Hensel’s lemma is then that \(g(X)\in \mathcal {O}^\flat [X]\). Next observe that the canonical projection \(\mathcal {O}^\flat \rightarrow \mathcal {O}/p\mathcal {O}\) has kernel \(p^\flat \mathcal {O}^\flat \) (Proof. Either argue using valuations, or extract a more general result from the proof of Lemma 8.), whence every monic polynomial in \(\mathcal {O}^\flat /p^\flat \mathcal {O}^\flat \) has a root. So, by lifting a root we find \(\beta \in \mathcal {O}^\flat \) satisfying \(g(\beta )\in p^\flat \mathcal {O}^\flat \); this implies that \(f(\alpha +c\beta )\in f(\beta ) p^{\flat }\mathcal {O}^\flat \), and so \(\varepsilon :=c\beta \) has the desired property.
- 57.
- 58.
By an easy induction using that p is a non-zero-divisor in \(\mathbb A_{{\mathrm {inf}}}/W(\mathfrak m)\), this follows from the fact that the maximal ideal of \(\mathbb A_{{\mathrm {inf}}}/p\mathbb A_{{\mathrm {inf}}}=\mathcal {O}^\flat \) is generated by the elements \(\varphi ^{-r}(\varepsilon )-1\), for all \(r\ge 0\).
References
Berthelot, P., and Ogus, A. Notes on crystalline cohomology. Princeton University Press, Princeton, N.J.; University of Tokyo Press, Tokyo, 1978.
Bhatt, B. Specializing varieties and their cohomology from characteristic 0 to characteristic \(p\). 43–88.
Bhatt, B., and Scholze, P. Prisms and prismatic cohomology. arXiv:1905.08229 (2019).
Bhatt, B., Morrow, M., and Scholze, P. Integral \(p\)-adic Hodge theory—announcement. Math. Res. Lett. 22, 6 (2015), 1601–1612.
Bhatt, B., Morrow, M., and Scholze, P. Integral \(p\)-adic Hodge theory. Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.
Bhatt, B., Morrow, M., and Scholze, P. Topological Hochschild homology and integral \(p\)-adic Hodge theory. Publ. Math. Inst. Hautes Études Sci. 129 (2019), 199–310.
Bloch, S., and Kato, K. \(p\)-adic étale cohomology. Inst. Hautes Études Sci. Publ. Math., 63 (1986), 107–152.
Caruso, X. Conjecture de l’inertie modérée de Serre. Invent. Math. 171, 3 (2008), 629–699.
\(\check{\rm C}\)esnavičius, K. e., and Koshikawa, T. The \(A_{inf}\)-cohomology in the semistable case. Compos. Math. 155, 11 (2019), 2039–2128.
Davis, C., and Kedlaya, K. S. On the Witt vector Frobenius. Proc. Amer. Math. Soc. 142, 7 (2014), 2211–2226.
Elkik, R. Solutions d’équations à coefficients dans un anneau hensélien. Ann. Sci. École Norm. Sup. (4) 6 (1973), 553–603 (1974).
Faltings, G. Crystalline cohomology and p-adic Galois-representations. In Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988). Johns Hopkins Univ. Press, Baltimore, MD, 1989, pp. 25–80.
Faltings, G. Integral crystalline cohomology over very ramified valuation rings. J. Amer. Math. Soc. 12, 1 (1999), 117–144.
Fontaine, J.-M. Exposé II: Les corps des périodes p-adiques. Avec un appendice par Pierre Colmez: Le nombres algébriques sont denses dans \(B_{dR}^+\). In Périodes \(p\)-adiques. Séminaire du Bures-sur-Yvette, France, 1988. Paris: Société Mathématique de France, 1994, pp. 59–111, appendix 103–111.
Fontaine, J.-M., and Messing, W. p-adic periods and p-adic étale cohomology. In Current trends in arithmetical algebraic geometry (Arcata, Calif., 1985), vol. 67 of Contemp. Math. Amer. Math. Soc., Providence, RI, 1987, pp. 179–207.
Huber, R. A generalization of formal schemes and rigid analytic varieties. Math. Z. 217, 4 (1994), 513–551.
Huber, R. Étale cohomology of rigid analytic varieties and adic spaces. Aspects of Mathematics, E30. Friedr. Vieweg & Sohn, Braunschweig, 1996.
Illusie, L. Complexe de de Rham-Witt et cohomologie cristalline. Ann. Sci. École Norm. Sup. (4) 12, 4 (1979), 501–661.
Illusie, L., and Raynaud, M. Les suites spectrales associées au complexe de de Rham-Witt. Inst. Hautes Études Sci. Publ. Math., 57 (1983), 73–212.
Kedlaya, K. Some ring-theoretic properties of \(A_{inf}\). Available at the author’s webpage (2016).
Lang, J., and Ludwig, J. \(\bf A\it _{\text{inf}}\) is infinite dimensional. arXiv:1906.03583 (2019).
Langer, A., and Zink, T. De Rham-Witt cohomology for a proper and smooth morphism. J. Inst. Math. Jussieu 3, 2 (2004), 231–314.
NizioŁ, W. Crystalline conjecture via \(K\)-theory. Ann. Sci. École Norm. Sup. (4) 31, 5 (1998), 659–681.
Scholze, P. Perfectoid spaces. Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.
Scholze, P. \(p\)-adic Hodge theory for rigid-analytic varieties. Forum Math. Pi 1 (2013), e1, 77.
Scholze, P. Canonical \(q\)-deformations in arithmetic geometry. Ann. Fac. Sci. Toulouse Math. (6) 26, 5 (2017), 1163–1192.
Théorie des topos et cohomologie étale des schémas. Tome 2. Lecture Notes in Mathematics, Vol. 270. Springer-Verlag, Berlin-New York, 1972. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat.
Tsuji, T. \(p\)-adic étale cohomology and crystalline cohomology in the semi-stable reduction case. Invent. Math. 137, 2 (1999), 233–411.
Acknowledgements
It is a pleasure to take this chance to thank my coauthors Bhargav Bhatt and Peter Scholze for the discussions and collaboration underlying [5], from which all results in these notes are taken. I am also grateful to the participants of the mini-course at l’IMJ on which these notes are based, including J.-F. Dat, C. Cornut, L. Fargues, J.-M. Fontaine, M.-H. Nicole, and B. Klingler, for their many helpful comments and insightful questions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: \(\mathbb A_{{\mathrm {inf}}}\) and Its Modules
The base ring for the cohomology theory constructed in [5] is Fontaine’s infinitesimal period ring \(\mathbb A_{{\mathrm {inf}}}:=W(\mathcal {O}^\flat )\), where \(\mathcal {O}\) is the ring of integers of a complete, non-archimedean, algebraically closed field \(\mathbb C\) of mixed characteristic. Since \(\mathcal {O}\) is a perfectoid ring (Example 2), the general theory developed in Sect. 3 (including Sect. 3.3) applies in particular to \(\mathcal {O}\). Our goal here is firstly to present a few results which are particular to \(\mathcal {O}\) in order to familiarise the reader, who may be encountering these objects for the first time, with \(\mathcal {O}\) and \(\mathbb A_{{\mathrm {inf}}}\); then we will explain some of the finer theory of modules over \(\mathbb A_{{\mathrm {inf}}}\).
We begin by recalling from [24, Sect. 3] that \(\mathcal {O}^\flat \) is the ring of integers of \(\mathbb C^\flat :={{\,\mathrm{Frac}\,}}\mathcal {O}^\flat \) (footnote 10 shows that \(\mathcal {O}^\flat \) is an integral domain), which is a non-archimedean, algebraically closed field of characteristic \(p>0\), with the same residue field k as \(\mathcal {O}\). The absolute value on \(\mathbb C^\flat \) is given by multiplicatively extending the absolute value on \(\mathcal {O}^\flat \) given by
where the first arrow uses the convention introduced just before Lemma 5, and the second arrow is the absolute value on \(\mathcal {O}\). The reader may wish to check that this is indeed an absolute value, i.e., satisfies the ultrametric inequality, that \(\mathbb C^\flat \) is complete under it, and that the ring of integers is exactly \(\mathcal {O}^\flat \). The existence of the canonical projection \(\mathcal {O}^\flat \rightarrow \mathcal {O}/p\mathcal {O}\) implies that \(\mathcal {O}^\flat \) and \(\mathcal {O}\) have the same residue field. Hensel’s lemma shows that \(\mathbb C^\flat \) is algebraically closed.Footnote 56
Now we turn to \(\mathbb A_{{\mathrm {inf}}}\). Let \(t\in \mathbb A_{{\mathrm {inf}}}\) be any element whose image in \(\mathbb A_{{\mathrm {inf}}}/p\mathbb A_{{\mathrm {inf}}}=\mathcal {O}^\flat \) belongs to \(\mathfrak m^\flat \setminus \{0\}\); examples include \(t=[\pi ]\), where \(\pi \in \mathfrak m^\flat \setminus \{0\}\), and \(t=\xi \), where \(\xi \) is any generator of \({\text {Ker}}\,\theta \). Then p, t is a regular sequence, and \(\mathbb A_{{\mathrm {inf}}}\) is a \(\langle p,t \rangle \)-adically complete local ring whose maximal ideal equals the radical of \(\langle p,t \rangle \); in short, \(\mathbb A_{{\mathrm {inf}}}\) “appears two-dimensional and Cohen–Macaulay”.
In fact, as we will explain the result of this appendix, modules (more precisely, finitely presented modules which become free after inverting p) over \(\mathbb A_{{\mathrm {inf}}}\) even behave as though \(\mathbb A_{{\mathrm {inf}}}\) were a two-dimensional, regular local ring.Footnote 57 Further details may be found in [5, Sect. 4.2].
Remark 11
In light of the goal, it is sensible to recall the structure of modules over any two-dimensional regular local ring \(\varLambda \), such as \(\varLambda =\mathcal {O}_K[[T]]\) where \(\mathcal {O}_K\) is a discrete valuation ring. Let \(\pi ,t\in \varLambda \) be a system of local parameters and \(\mathfrak m=\langle \pi ,t \rangle \) its maximal ideal.
-
(i)
Most importantly, any vector bundle on the punctured spectrum \({{\,\mathrm{Spec}\,}}\varLambda \setminus \{\mathfrak m\}\) extends uniquely to a vector bundle on \({{\,\mathrm{Spec}\,}}\varLambda \).
-
(ii)
Finitely generated modules over \(\varLambda \) are perfect, i.e., admit finite length resolutions by finite free \(\varLambda \)-modules. (Proof. Immediate from the regularity of \(\varLambda \).)
-
(iii)
If M is any finitely generated \(\varLambda \)-module, then there is a functorial short exact sequence
$$\begin{aligned} 0\longrightarrow M_{{\mathrm {tor}}}\longrightarrow M\longrightarrow M_{{\mathrm {free}}}\longrightarrow \overline{M}\longrightarrow 0 \end{aligned}$$of \(\varLambda \)-modules, where \(M_{{\mathrm {tor}}}\) is torsion, \(M_{{\mathrm {free}}}\) is finite free, and \(\overline{M}\) is killed by a power of \(\mathfrak m\).
Proof. \(M_{{\mathrm {tor}}}\) is by definition the torsion submodule of M, whence \(M/M_{{\mathrm {tor}}}\) restricts to a torsion-free coherent sheaf on the punctured spectrum \({{\,\mathrm{Spec}\,}}\varLambda \setminus \{\mathfrak m\}\); but the punctured spectrum is a regular one-dimensional scheme, so this torsion-free coherent sheaf is necessary a vector bundle, and so extends to a vector bundle on \({{\,\mathrm{Spec}\,}}\varLambda \) by (i); this vector bundle corresponds to a finite free \(\varLambda \)-module \(M_{{\mathrm {free}}}\) which contains \(M/M_{{\mathrm {tor}}}\), with the ensuing quotient \(\overline{M}\) being supported at the closed point of \({{\,\mathrm{Spec}\,}}\varLambda \).
-
(iv)
Finite projective modules over \(\varLambda [\tfrac{1}{\pi }]\) are finite free.
Proof. Let N be a finite projective \(\varLambda [\tfrac{1}{\pi }]\)-module, and pick a finitely generated \(\varLambda \)-module \(N'\subseteq N\) satisfying \(N'[\tfrac{1}{\pi }]=N\). Then \(N'_\mathfrak p\) is a projective module over \(\varLambda _\mathfrak p\) for every non-maximal prime ideal \(\mathfrak p\subseteq \varLambda \): indeed either \(\pi \notin \mathfrak p\), in which case \(N'_\mathfrak p\) is a localisation of the projective module N, or \(\mathfrak p=\langle \pi \rangle \), in which case \(\varLambda _\mathfrak p\) is a discrete valuation ring and it is sufficient to note that \(N_\mathfrak p'\) obviously has no \(\pi \)-torsion. This means that \(N'\) restricts to a vector bundle on the punctured spectrum, whose unique extension to a finite free \(\varLambda \)-module \(N''\) satisfies \(N''[\tfrac{1}{\pi }]=N\).
Theorem 11
-
(i)
(Kedlaya) Any vector bundle on the punctured spectrum
$$\begin{aligned} {{\,\mathrm{Spec}\,}}\mathbb A_{{\mathrm {inf}}}\setminus \{\text {the max. ideal of }\mathbb A_{{\mathrm {inf}}}\} \end{aligned}$$extends uniquely to a vector bundle on \({{\,\mathrm{Spec}\,}}\mathbb A_{{\mathrm {inf}}}\).
-
(ii)
If M is a finitely presented \(\mathbb A_{{\mathrm {inf}}}\)-module such that \(M[\tfrac{1}{p}]\) is finite free over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\), then M is perfect (again, this means that M admits a finite length resolution by finite free \(\mathbb A_{{\mathrm {inf}}}\)-modules).
-
(iii)
If M is a finitely presented \(\mathbb A_{{\mathrm {inf}}}\)-module such that \(M[\tfrac{1}{p}]\) is finite free over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\), then there is functorial short exact sequence of \(\mathbb A_{{\mathrm {inf}}}\)-modules
$$\begin{aligned} 0\longrightarrow M_{{\mathrm {tor}}}\longrightarrow M\longrightarrow M_{{\mathrm {free}}}\longrightarrow \overline{M}\longrightarrow 0 \end{aligned}$$such that: \(M_{{\mathrm {tor}}}\) is a perfect \(\mathbb A_{{\mathrm {inf}}}\)-module killed by a power of p; \(M_{{\mathrm {free}}}\) is a finite free \(\mathbb A_{{\mathrm {inf}}}\)-module; and \(\overline{M}\) is a perfect \(\mathbb A_{{\mathrm {inf}}}\)-module killed by a power of the ideal \(\langle p,t \rangle \).
-
(iv)
Finite projective modules over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\) are finite free.
Proof
We have nothing to say about (i) here, and refer instead to [5, Lemma 4.6]. We will also only briefly comment on the remaining parts of the theorem, since these self-contained results may be easily read in [5, Sect. 4.2].
(ii) By clearing denominators in a basis for \(M[\tfrac{1}{p}]\) to construct a finite free \(\mathbb A_{{\mathrm {inf}}}\)-module \(M'\subseteq M\) satisfying \(M'[\tfrac{1}{p}]=M[\tfrac{1}{p}]\), we may reduce to the case that M is killed by a power of p, i.e., M is a \(\mathbb A_{{\mathrm {inf}}}/p^r\mathbb A_{{\mathrm {inf}}}=W_r(\mathcal {O}^\flat )\)-module for some \(r\gg 0\). By an induction on r, using that \(W_r(\mathcal {O}^\flat )\) can be shown to be coherent [5, Proposition 3.24] (this is not a trivial result), one can reduce to the case \(r=1\), in which case it easily follows from the classification of finitely presented modules over the valuation ring \(\mathcal {O}^\flat \): they have the shape \((\mathcal {O}^\flat )^n\oplus \mathcal {O}^\flat /a_1\mathcal {O}^\flat \oplus \cdots \oplus \mathcal {O}^\flat /a_m\mathcal {O}^\flat \), for some \(n\ge 1\) and \(a_i\in \mathcal {O}^\flat \), and so in particular are perfect.
(iii) This is proved similarly to the analogous assertion in the previous remark.
(iv) This is proved exactly as the analogous assertion in the previous remark, once it is checked that the localisation \(\mathbb A_{{\mathrm {inf}},\langle p \rangle }\) is a discrete valuation ring.
Corollary 5
Let M be a finitely presented \(\mathbb A_{{\mathrm {inf}}}\)-module such that \(M[\tfrac{1}{p}]\) is finite free over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\). If either \(M\otimes _{\mathbb A_{{\mathrm {inf}}}}W(k)\) or \(M\otimes _{\mathbb A_{{\mathrm {inf}}}}\mathcal {O}\) is p-torsion-free (equivalently, finite free over W(k) or \(\mathcal {O}\) respectively), then M is a finite free \(\mathbb A_{{\mathrm {inf}}}\)-module.
Proof
It follows easily from the hypothesis that the map \(M\rightarrow M_{{\mathrm {free}}}\) in Theorem 11(iii) becomes an isomorphism after tensoring by W(k) or \(\mathcal {O}\); hence \(M[\tfrac{1}{p}]\) and \(M\otimes _{\mathbb A_{{\mathrm {inf}}}}k\) have the same rank over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\) and k respectively. But an easy Fitting ideal argument shows that if N is a finitely presented module over a local integral domain R satisfying \(\dim _{{{\,\mathrm{Frac}\,}}R}(N\otimes _R{{\,\mathrm{Frac}\,}}R)=\dim _{k(R)}(N\otimes _Rk(R))\), then N is finite free over R.
To state and prove the next corollary we use the elements \(\xi ,\xi _r,\mu \in \mathbb A_{{\mathrm {inf}}}\) constructed in Sect. 3.3:
Corollary 6
Let M be a finitely presented \(\mathbb A_{{\mathrm {inf}}}\)-module, and assume:
-
\(M[\tfrac{1}{p\mu }]\) is a finite free \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p\mu }]\)-module of the same rank as the W(k)-module \(M\otimes _{\mathbb A_{{\mathrm {inf}}}}W(k)\).
-
There exists a Frobenius-semi-linear endomorphism of M which becomes an isomorphism after inverting \(\xi \).
Then \(M[\tfrac{1}{p}]\) is finite free over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\).
Proof
We must show that each Fitting ideal of the \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\)-module \(M[\tfrac{1}{p}]\) is either 0 or \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\); indeed, this means exactly that \(M[\tfrac{1}{p}]\) is finite projective over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\), which is sufficient by Theorem 11(iv). Since Fitting ideals behave well under base change, it is equivalent to prove that the first non-zero Fitting ideal \(J\subseteq \mathbb A_{{\mathrm {inf}}}\) of M contains a power of p. Again using that Fitting ideals base change well, our hypotheses imply that \(J\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p\mu }]=\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p\mu }]\) and \(JW(k)\ne 0\); that is, J contains a power of \(p\mu \) and \(J+W(\mathfrak m^\flat )\) contains a power of p, where \(W(\mathfrak m^\flat ):={\text {Ker}}(\mathbb A_{{\mathrm {inf}}}\rightarrow W(k))\). Because of the existence of the Frobenius on M, we also know that J and \(\varphi (J)\) are equal up to a power of \(\varphi (\xi )\). In conclusion, we may pick \(N\gg \) such that
-
(i)
\((p\mu )^N\in J\);
-
(ii)
\(p^N\in J+W(\mathfrak m)\);
-
(iii)
\(\varphi (\xi )^N\varphi (J)\subseteq J\) and \(\varphi (\xi )^NJ\subseteq \varphi (J)\).
Since \(W(\mathfrak m)\) is the p-adic completion of the ideal generated by \(\varphi ^{-r}(\mu ^N)\), for all \(r\ge 0\),Footnote 58 observation (ii) lets us write \(p^N=\alpha +\beta \varphi ^{-r}(\mu ^N)+\beta 'p^{N+1}\) for some \(\alpha \in J\) and \(\beta ,\beta '\in \mathbb A_{{\mathrm {inf}}}\), and \(r\ge 0\). Since \(1-\beta 'p\) is invertible, we may easily suppose that \(\beta '=0\), i.e., \(p^N=\alpha +\beta \varphi ^{-r}(\mu ^N)\). Multiplying through by \(p^N\xi _r^N\) gives \(\xi _r^Np^{2N}=p^N\xi _r^N\alpha +\beta p^N\mu ^N\), which belongs to J by (i) and (ii).
We claim, for any \(a,i\ge 1\), that
A trivial induction then shows that J contains a power of p, thereby completing the proof, and so it remains only to prove this claim. Suppose \(\xi _r^ap^b\in J\) for some \(a,b,i\ge 1\). Then \(\varphi ^r(\xi _r)^ap^b\in \varphi ^r(J)\), and so \(\varphi ^r(\xi _r)^{a+N}p^b\in J\) (since an easy generalisation of (iii) implies that \(\varphi ^r(\xi _r)^N\varphi ^r(J)\subseteq J\)). But \(\varphi ^r(\xi _r)\equiv p^r\) mod \(\xi _r\), so we may write \(\varphi ^r(\xi _r)^{a+N}=p^{r(a+N)}+\alpha \xi _r\) for some \(\alpha \in \mathbb A_{{\mathrm {inf}}}\) and thus deduce that \(J\ni (p^{r(a+N)}+\alpha \xi _r)p^b=p^{r(a+N)+b}+\alpha \xi _rp^b\). Now multiply through by \(\xi _r^{a-1}\) and use the supposition to obtain \(\xi _r^{a-1}p^{r(a+N)+b}\in J\), as required.
We will also need the following to eliminate the appearance of higher Tors in the crystalline specialisation of the \(\mathbb A_{{\mathrm {inf}}}\)-cohomology theory:
Lemma 22
Let M be an \(\mathbb A_{{\mathrm {inf}}}\)-module such that \(M[\tfrac{1}{p}]\) is flat over \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\). Then \({{\,\mathrm{Tor}\,}}_*^{\mathbb A_{{\mathrm {inf}}}}(M,W(k))=0\) for \(*>1\).
Proof
Let \([\mathfrak m^\flat ]\subseteq W(\mathfrak m^\flat )\) be the ideal of \(\mathbb A_{{\mathrm {inf}}}\) which is generated by Teichmüller lifts of elements of \(\mathfrak m^\flat \). We first observe that \(\mathbb A_{{\mathrm {inf}}}/[\mathfrak m^\flat ]\) is p-torsion-free and has Tor-dimension \(=1\) over \(\mathbb A_{{\mathrm {inf}}}\): indeed, \([\mathfrak m^\flat ]\) is the increasing union of the ideals \([\pi ]\mathbb A_{{\mathrm {inf}}}\), for \(\pi \in \mathfrak m^\flat \setminus \{0\}\), and the claims are true for \(\mathbb A_{{\mathrm {inf}}}/[\pi ]\mathbb A_{{\mathrm {inf}}}\) since \(p,[\pi ]\) is a regular sequence of \(\mathbb A_{{\mathrm {inf}}}\).
Next, since \(W_r(\mathfrak m^\flat )\) is generated by the analogous Teichmüller lifts in \(W_r(\mathcal {O}^\flat )=\mathbb A_{{\mathrm {inf}}}/p^r\mathbb A_{{\mathrm {inf}}}\), for any \(r\ge 1\) (c.f., footnote 20), the quotient \(W(\mathfrak m^\flat )/[\mathfrak m^\flat ]\) is p-divisible. Combined with the previous observation, it follows that \(W(\mathfrak m^\flat )/[\mathfrak m^\flat ]\) is uniquely p-divisible, i.e., an \(\mathbb A_{{\mathrm {inf}}}[\tfrac{1}{p}]\)-module, whence
which vanishes for \(*>0\) by the hypothesis on M. Combining this with the short exact sequence
and the initial observation about the Tor-dimension of the middle term completes the proof.
Appendix 2: Two Lemmas on Koszul Complexes
Let R be a ring, and \(g_1,\ldots ,g_d\in R\). The associated Koszul complex will be denoted by \(K_R(g_1,\ldots ,g_d)=\bigotimes _{i=1}^d K_R(g_i)\), where \(K_R(g_i):=[R\xrightarrow {g_i}R]\). Here we state two useful lemmas concerning such complexes, the second of which describes the behaviour of the décalage functor.
Lemma 23
Let \(g\in R\) be an element which divides \(g_1,\ldots ,g_d\), and such that \(g_i\) divides g for some i. Then there are isomorphisms of R-modules
for all \(n\ge 0\).
Proof
[5, Lemma 7.10].
Lemma 24
Let \(f\in R\) be a non-zero-divisor such that, for each i, either f divides \(g_i\) or \(g_i\) divides f. Then:
-
If f divides \(g_i\) for all i, then \(\eta _f K_R(g_1,\ldots ,g_d)\cong K_R(g_1/f,\ldots ,g_d/f)\).
-
If \(g_i\) divides f for some i, then \(\eta _f K_R(g_1,\ldots ,g_d)\) is acyclic.
Proof
[5, Lemma 7.9].
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Morrow, M. (2020). Notes on the \(\mathbb A_{{\mathrm {inf}}}\)-Cohomology of Integral p-Adic Hodge Theory. In: Bhatt, B., Olsson, M. (eds) p-adic Hodge Theory. Simons Symposia. Springer, Cham. https://doi.org/10.1007/978-3-030-43844-9_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-43844-9_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-43843-2
Online ISBN: 978-3-030-43844-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


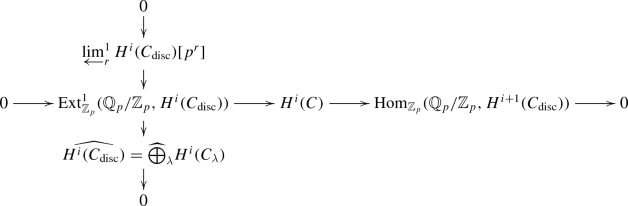
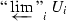 and
and  by “obviously isomorphic” towers, e.g., by inserting or removing some stages of the tower. To be precise, first let
by “obviously isomorphic” towers, e.g., by inserting or removing some stages of the tower. To be precise, first let 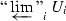 in
in 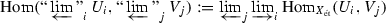 . Then call an object
. Then call an object 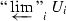 whose transition maps are finite étale surjective; and call a morphism
whose transition maps are finite étale surjective; and call a morphism 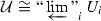 and
and 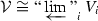 in
in  and
and 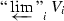 have finite étale surjective transition maps and such that the resulting morphism
have finite étale surjective transition maps and such that the resulting morphism 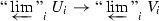 has the shape described in the main text. Then the category
has the shape described in the main text. Then the category