Abstract
The collision probability tester, introduced by Goldreich and Ron (ECCC, TR00-020, 2000), distinguishes the uniform distribution over [n] from any distribution that is \(\epsilon \)-far from this distribution using \(\mathrm{poly}(1/\epsilon )\cdot {\sqrt{n}}\) samples. While the original analysis established only an upper bound of \(O(1/\epsilon )^4\cdot {\sqrt{n}}\) on the sample complexity, a recent analysis of Diakonikolas, Gouleakis, Peebles, and Price (ECCC, TR16-178, 2016) established the optimal upper bound of \(O(1/\epsilon )^2\cdot {\sqrt{n}}\). In this note we survey their analysis, while highlighting the sources of improvement. Specifically:
-
1.
While the original analysis reduces the testing problem to approximating the collision probability of the unknown distribution up to a \(1+\epsilon ^2\) factor, the improved analysis capitalizes on the fact that the latter problem needs only be solved “at the extreme” (i.e., it suffices to distinguish the uniform distribution, which has collision probability 1/n, from any distribution that has collision probability exceeding \((1+4\epsilon ^2)/n\)).
-
2.
While the original analysis provides an almost optimal analysis of the variance of the estimator when \(\epsilon =\varOmega (1)\), a more careful analysis yields a significantly better bound for the case of \(\epsilon =o(1)\), which is the case that is relevant here.
A preliminary version of this exposition was posted in September 2017 as Comment Nr. 1 on TR16-178 of ECCC. The current revision is quite minimal, although some typos were fixed and some of the discussions were improved.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Although testing properties of distributions was briefly discussed in [10, Sec. 3.4.3], its study was effectively initiated in [4]. The starting point of [4] was a test of uniformity, which was implicit in [11], where it is applied to test the distribution of the endpoint of a relatively short random walk on a bounded-degree graph. Generalizing this tester of uniformity, Batu et al. [3, 4] presented testers for the property consisting of pairs of identical distributions as well as for all properties consisting of any single distribution (where the property \(\{U_n\}\) is a special case).
- 2.
- 3.
That is, use \(\sum _{i\in [n]}|p(i)-n^{-1}|\cdot 1 \le \left( \sum _{i\in [n]}|p(i)-n^{-1}|^2\right) ^{1/2} \cdot \left( \sum _{i\in [n]}1^2\right) ^{1/2}\).
- 4.
A random variable X (resp., an algorithm) is called an unbiased estimator of a quantity v if \(\mathbb E[X]=v\) (resp., the expected value of its output equals v). Needless to say, the key question with respect to the usefulness of such an estimator is the magnitude of its variance (and, specifically, the relation between its variance and the square of its expectation). For example, for any NP-witness relation
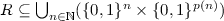 , the (trivial) algorithm that on input x selects at random \(y\in \{0,1\}^{p(|x|)}\) and outputs \(2^{p(|x|)}\) if and only if \((x,y)\in R\), is an unbiased estimator of the number of witnesses for x, whereas counting the number of NP-witnesses is notoriously hard. The catch is, of course, that this estimation has a huge variance; letting \(\rho (x)>0\) denote the fraction of witnesses for x, this estimator has expected value \(\rho (x)\cdot 2^{p(|x|)}\) whereas its variance is \((\rho (x)-\rho (x)^2)\cdot 2^{2\cdot p(|x|)}\), which is typically much larger than the expectation squared (i.e., when \(0<\rho (x)\ll 1/\mathrm{poly}(|x|)\)).
, the (trivial) algorithm that on input x selects at random \(y\in \{0,1\}^{p(|x|)}\) and outputs \(2^{p(|x|)}\) if and only if \((x,y)\in R\), is an unbiased estimator of the number of witnesses for x, whereas counting the number of NP-witnesses is notoriously hard. The catch is, of course, that this estimation has a huge variance; letting \(\rho (x)>0\) denote the fraction of witnesses for x, this estimator has expected value \(\rho (x)\cdot 2^{p(|x|)}\) whereas its variance is \((\rho (x)-\rho (x)^2)\cdot 2^{2\cdot p(|x|)}\), which is typically much larger than the expectation squared (i.e., when \(0<\rho (x)\ll 1/\mathrm{poly}(|x|)\)). - 5.
In fact, one typically derives the standard bound earlier by using \(\mathbb E[{\overline{\zeta }}_{1,2}{\overline{\zeta }}_{2,3}]\le \mathbb E[\zeta _{1,2}\zeta _{2,3}]=\tau \) (instead of \(\mathbb E[{\overline{\zeta }}_{1,2}{\overline{\zeta }}_{2,3}]=\tau -\mu ^2\)), and noting that \(\tau \le \mu ^{3/2}\).
- 6.
Let \(s=c\cdot {\sqrt{n}}/\eta \) for some constant c. Then, when upper-bounding the first and last terms, use \(s^2\cdot \delta ^2\cdot n > c^2\cdot (n/\eta ^2)\cdot (2\eta /n)^2\cdot n=4c^2\). When upper-bounding the second and third terms, use \(s^2\cdot \delta >c^2\cdot (n/\eta ^2)\cdot (2\eta /n)\ge 2c^2\), where the last inequality uses \(\eta \le 1\).
- 7.
For example, a distribution that assigns mass \(0.1\epsilon \) to a single point and is uniform on the other \(n-1\) points is \(0.1\epsilon \)-close to \(U_n\) but has collision probability greater than \((0.1\cdot \epsilon )^2\), whereas a distribution that with probability \(0.5+3\epsilon \) is uniform on [n/2] and otherwise is uniform on \(\{(n/2)+1,...,n\}\) is \(2\epsilon \)-far from \(U_n\) but has collision probability \((1+12\epsilon ^2)/n\). Actually, the foregoing “tolerant testing” task (i.e., distinguishing distributions that are \(0.1\cdot \epsilon \)-close to \(U_n\) from distributions that are \(\epsilon \)-far from \(U_n\)) has sample complexity \(\varOmega (n/\log n)\); see [14].
References
Acharya, J., Daskalakis, C., Kamath, G.: Optimal testing for properties of distributions. arXiv:1507.05952 [cs.DS] (2015)
Badescu, C., O’Donnell, R., Wright, J.: Quantum state certification. arXiv:1708.06002 [quant-ph] (2017)
Batu, T., Fischer, E., Fortnow, L., Kumar, R., Rubinfeld, R., White, P.: Testing random variables for independence and identity. In: 42nd IEEE Symposium on Foundations of Computer Science, pp. 442–451 (2001)
Batu, T., Fortnow, L., Rubinfeld, R., Smith, W.D., White, P.: Testing that distributions are close. In: 41st IEEE Symposium on Foundations of Computer Science, pp. 259–269 (2000)
Chan, S., Diakonikolas, I., Valiant, P., Valiant, G.: Optimal algorithms for testing closeness of discrete distributions. In: 25th ACM-SIAM Symposium on Discrete Algorithms, pp. 1193–1203 (2014)
Diakonikolas, I., Kane, D.: A new approach for testing properties of discrete distributions. arXiv:1601.05557 [cs.DS] (2016)
Diakonikolas, I., Kane, D., Nikishkin, V.:Testing identity of structured distributions. In: 26th ACM-SIAM Symposium on Discrete Algorithms, pp. 1841–1854 (2015)
Diakonikolas, I., Gouleakis, T., Peebles, J., Price, E.: Collision-based testers are optimal for uniformity and closeness. ECCC, TR16-178 (2016)
Goldreich, O.: Introduction to Property Testing. Cambridge University Press, Cambridge (2017)
Goldreich, O., Goldwasser, S., Ron, D.: Property testing and its connection to learning and approximation. J. ACM 45(4), 653–750 (1998). Extended abstract in 37th IEEE Symposium on Foundations of Computer Science, 1996
Goldreich, O., Ron, D.: On testing expansion in bounded-degree graphs. ECCC, TR00-020 (2000)
O’Donnell, R., Wright, J.: A primer on the statistics of longest increasing subsequences and quantum states. To appear in SIGACT News
Paninski, L.: A coincidence-based test for uniformity given very sparsely-sampled discrete data. IEEE Trans. Inf. Theory 54, 4750–4755 (2008)
Valiant, G., Valiant, P.: A CLT and tight lower bounds for estimating entropy. ECCC, TR10-179 (2010)
Acknowledgements
I am grateful to Ryan O’Donnell for many helpful discussions regarding the result of [8]. Ryan, in turn, claims to have been benefitting from his collaborators on [2, 12], and was also inspired by [1]. Hence, my thanks are extended to all contributors to these works as well as to the contributers to [8].
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Goldreich, O. (2020). On the Optimal Analysis of the Collision Probability Tester (an Exposition). In: Goldreich, O. (eds) Computational Complexity and Property Testing. Lecture Notes in Computer Science(), vol 12050. Springer, Cham. https://doi.org/10.1007/978-3-030-43662-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-43662-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-43661-2
Online ISBN: 978-3-030-43662-9
eBook Packages: Computer ScienceComputer Science (R0)





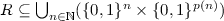 , the (trivial) algorithm that on input x selects at random
, the (trivial) algorithm that on input x selects at random