Relativistic Nucleus-Nucleus Collisions and the QCD Matter Phase Diagram

Abstract

This review will be concerned with our knowledge of extended matter under the governance of strong interaction, in short: QCD matter. Strictly speaking, the hadrons are representing the first layer of extended QCD architecture. In fact we encounter the characteristic phenomena of confinement as distances grow to the scale of 1 fm (i.e. hadron size): loss of the chiral symmetry property of the elementary QCD Lagrangian via non-perturbative generation of “massive” quark and gluon condensates, that replace the bare QCD vacuum. However, given such first experiences of transition from short range perturbative QCD phenomena (jet physics etc.), toward extended, non perturbative QCD hadron structure, we shall proceed here to systems with dimensions far exceeding the force range: matter in the interior of heavy nuclei, or in neutron stars, and primordial matter in the cosmological era from electro-weak decoupling (10⁻¹² s) to hadron formation (0.5 ⋅ 10⁻⁵ s). This primordial matter, prior to hadronization, should be deconfined in its QCD sector, forming a plasma (i.e. color conducting) state of quarks and gluons: the Quark Gluon Plasma (QGP).

7.1 Introduction

7.1.1 Overview

This review will be concerned with our knowledge of extended matter under the governance of strong interaction, in short: QCD matter. Strictly speaking, the hadrons are representing the first layer of extended QCD architecture. In fact we encounter the characteristic phenomena of confinement as distances grow to the scale of 1 fm (i.e. hadron size): loss of the chiral symmetry property of the elementary QCD Lagrangian via non-perturbative generation of “massive” quark and gluon condensates, that replace the bare QCD vacuum [1]. However, given such first experiences of transition from short range perturbative QCD phenomena (jet physics etc.), toward extended, non perturbative QCD hadron structure, we shall proceed here to systems with dimensions far exceeding the force range: matter in the interior of heavy nuclei, or in neutron stars, and primordial matter in the cosmological era from electro-weak decoupling (10⁻¹² s) to hadron formation (0.5 ⋅ 10⁻⁵ s). This primordial matter, prior to hadronization, should be deconfined in its QCD sector, forming a plasma (i.e. color conducting) state of quarks and gluons [2]: the Quark Gluon Plasma (QGP).

In order to recreate matter at the corresponding high energy density in the terrestrial laboratory one collides heavy nuclei (also called “heavy ions”) at ultrarelativistic energies. Quantum Chromodynamics predicts [2,3,4] a phase transformation to occur between deconfined quarks and confined hadrons. At near-zero net baryon density (corresponding to big bang conditions) non-perturbative Lattice-QCD places this transition at an energy density of about 1 GeV/fm³, and at a critical temperature, T _crit ≈ 170 MeV [4,5,6,7,8] (see the article on Lattice QCD in this Volume). The ultimate goal of the physics with ultrarelativistic heavy ions is to locate this transition, elaborate its properties, and gain insight into the detailed nature of the deconfined QGP phase that should exist above. What is meant by the term “ultrarelativistic” is defined by the requirement that the reaction dynamics reaches or exceeds the critical density 𝜖 ≈ 1 GeV/fm³. Required beam energies turn out [8] to be $\sqrt {s} \ge 10$ GeV, and various experimental programs have been carried out or are being prepared at the CERN SPS (up to about 20 GeV), at the BNL RHIC collider (up to 200 GeV) and finally reaching up to 5.5 TeV at the LHC of CERN.

QCD confinement-deconfinement is of course not limited to the domain that is relevant to cosmological expansion dynamics, at very small excess of baryon over anti-baryon number density and, thus, near zero baryo-chemical potential μ _B. In fact, modern QCD suggests [9,10,11] a detailed phase diagram of QCD matter and its states, in the plane of T and baryo-chemical potential μ _B. For a map of the QCD matter phase diagram we are thus employing the terminology of the grand canonical Gibbs ensemble that describes an extended volume V  of partonic or hadronic matter at temperature T. In it, total particle number is not conserved at relativistic energy, due to particle production-annihilation processes occurring at the microscopic level. However, the probability distributions (partition functions) describing the relative particle species abundances have to respect the presence of certain, to be conserved net quantum numbers (i), notably non-zero net baryon number and zero net strangeness and charm. Their global conservation is achieved by a thermodynamic trick, adding to the system Lagrangian a so-called Lagrange multiplier term, for each of such quantum number conservation tasks. This procedure enters a “chemical potential” μ _i that modifies the partition function via an extra term $\exp {\left (-\mu _i/T\right )}$ occurring in the phase space integral (see Sect. 7.3 for detail). It modifies the canonical “punishment factor” ($\exp {\left (-E/T\right )}$), where E is the total particle energy in vacuum, to arrive at an analogous grand canonical factor for the extended medium, of $\exp {\left (-E/T - \mu _i/T\right )}$. This concept is of prime importance for a description of the state of matter created in heavy ion collisions, where net-baryon number (valence quarks) carrying objects are considered—extended “fireballs” of QCD matter. The same applies to the matter in the interior of neutron stars. The corresponding conservation of net baryon number is introduced into the grand canonical statistical model of QCD matter via the “baryo-chemical potential” μ _B.

We employ this terminology to draw a phase diagram of QCD matter in Fig. 7.1, in the variables T and μ _B. Note that μ _B is high at low energies of collisions creating a matter fireball. In a head-on collision of two mass 200 nuclei at $\sqrt {s}=15$ GeV the fireball contains about equal numbers of newly created quark-antiquark pairs (of zero net baryon number), and of initial valence quarks. The accommodation of the latter, into created hadronic species, thus requires a formidable redistribution task of net baryon number, reflecting in a high value of μ _B. Conversely, at LHC energy (5.5 TeV for Pb+Pb collisions), the initial valence quarks constitute a mere 5% fraction of the total quark density, correspondingly requiring a small value of μ _B. In the extreme, big bang matter evolves toward hadronization (at T=170 MeV) featuring a quark over antiquark density excess of 10⁻⁹ only, resulting in μ _B ≈ 0.

Fig. 7.1

Sketch of the QCD matter phase diagram in the plane of temperature T and baryo-chemical potential μ _B. The parton-hadron phase transition line from lattice QCD [8,9,10,11] ends in a critical point E. A cross-over transition occurs at smaller μ _B. Also shown are the points of hadro-chemical freeze-out from the grand canonical statistical model

Note that the limits of existence of the hadronic phase are not only reached by temperature increase, to the so-called Hagedorn value T _H (which coincides with T _crit at μ _B → 0), but also by density increase to ϱ > (5–10) ϱ ₀: “cold compression” beyond the nuclear matter ground state baryon density ϱ ₀ of about 0.16 B/fm³. We are talking about the deep interior sections of neutron stars or about neutron star mergers [12,13,14]. A sketch of the present view of the QCD phase diagram [9,10,11] is given in Fig. 7.1.

It is dominated by the parton-hadron phase transition line that interpolates smoothly between the extremes of predominant matter heating (high T, low μ _B) and predominant matter compression (T → 0, μ _B > 1 GeV). Onward from the latter conditions, the transition is expected to be of first order [15] until the critical point of QCD matter is reached at 200 ≤ μ _B (E)  ≤ 500 MeV. The relatively large position uncertainty reflects the preliminary character of Lattice QCD calculations at finite μ _B [9,10,11]. Onward from the critical point, E, the phase transformation at lower μ _B is a cross-over[11].

We note, however, that these estimates represent a major recent advance of lattice theory which was, for two decades, believed to be restricted to the μ _B = 0 situation. Onward from the critical point, toward lower μ _B, the phase transformation should acquire the properties of a rapid cross-over [16], thus also including the case of primordial cosmological expansion. This would finally rule out former ideas, based on the picture of a violent first order “explosive” cosmological hadronization phase transition, that might have caused non-homogeneous conditions, prevailing during early nucleo-synthesis [17], and fluctuations of global matter distribution density that could have served as seedlings of galactic cluster formation [18]. However, it needs to be stressed that the conjectured order of phase transformation, occurring along the parton-hadron phase boundary line, has not been unambiguously confirmed by experiment, as of now.

On the other hand, the position of the QCD phase boundary at low μ _B has, in fact, been located by the hadronization points in the T, μ _B plane that are also illustrated in Fig. 7.1. They are obtained from statistical model analysis [19] of the various hadron multiplicities created in nucleus-nucleus collisions, which results in a [T, μ _B] determination at each incident energy, which ranges from SIS via AGS and SPS to RHIC energies, i.e. $3\le \sqrt {s} \le 200$ GeV. Toward low μ _B these hadronic freeze-out points merge with the lattice QCD parton-hadron coexistence line: hadron formation coincides with hadronic species freeze-out. These points also indicate the μ _B domain of the phase diagram which is accessible to relativistic nuclear collisions. The domain at μ _B ≥ 1.5 GeV which is predicted to be in a further new phase of QCD featuring color-flavor locking and color superconductivity [20] will probably be accessible only to astrophysical observation.

One may wonder how states and phases of matter in thermodynamical equilibrium—as implied by a description in grand canonical variables—can be sampled via the dynamical evolution of relativistic nuclear collisions. Employing heavy nuclei, A ≈ 200, as projectiles/targets or in colliding beams (RHIC, LHC), transverse dimensions of the primordial interaction volume do not exceed about 8 fm, and strong interaction ceases after about 20 fm/c. We shall devote an entire later section to the aspects of equilibrium (Sect. 7.2.5) but note, for now, that the time and dimension scale of primordial perturbative QCD interaction at the microscopic partonic level amounts to subfractions of 1 fm/c, the latter scale, however, being representative of non perturbative processes (confinement, “string” formation etc.). The A+A fireball size thus exceeds, by far, the elementary non perturbative scale. An equilibrium quark gluon plasma represents an extended non-perturbative QCD object, and the question whether its relaxation time scale can be provided by the expansion time scale of an A+A collision, needs careful examination. Reassuringly, however, the hadrons that are supposedly created from such a preceding non-perturbative QGP phase at top SPS and RHIC energy, do in fact exhibit perfect hadrochemical equilibrium, the derived [T, μ _B] values [19] thus legitimately appearing in the phase diagram, Fig. 7.1.

In the present review we will order the physics observables to be treated, in sequence of their origin from successive stages that characterize the overall dynamical evolution of a relativistic nucleus-nucleus collision. In rough outline this evolution can be seen to proceed in three major steps. An initial period of matter compression and heating occurs in the course of interpenetration of the projectile and target baryon density distributions. Inelastic processes occurring at the microscopic level convert initial beam longitudinal energy to new internal and transverse degrees of freedom, by breaking up the initial baryon structure functions. Their partons thus acquire virtual mass, populating transverse phase space in the course of inelastic perturbative QCD shower multiplication. This stage should be far from thermal equilibrium, initially. However, in step two, inelastic interaction between the two arising parton fields (opposing each other in longitudinal phase space) should lead to a pile-up of partonic energy density centered at mid-rapidity (the longitudinal coordinate of the overall center of mass). Due to this mutual stopping down of the initial target and projectile parton fragmentation showers, and from the concurrent decrease of parton virtuality (with decreasing average square momentum transfer Q ²) there results a slowdown of the time scales governing the dynamical evolution. Equilibrium could be approached here, the system “lands” on the T, μ plane of Fig. 7.1, at temperatures of about 300 and 200 MeV at top RHIC and top SPS energy, respectively. The third step, system expansion and decay, thus occurs from well above the QCD parton-hadron boundary line. Hadrons and hadronic resonances then form, which decouple swiftly from further inelastic transmutation so that their yield ratios become stationary (“frozen-out”). A final expansion period dilutes the system to a degree such that strong interaction ceases all together.

In order to verify in detail this qualitative overall model, and to ascertain the existence (and to study the properties) of the different states of QCD that are populated in sequence, one seeks observable physics quantities that convey information imprinted during distinct stages of the dynamical evolution, and “freezing-out” without significant obliteration by subsequent stages. Ordered in sequence of their formation in the course of the dynamics, the most relevant such observables are briefly characterized below:

• 1. Suppression of J∕ Ψ and Y  production by Debye-screening in the QGP. These vector mesons result from primordial, pQCD production of $c\overline {c}$ and $b\overline {b}$ pairs that would hadronize unimpeded in elementary collisions but are broken up if immersed into a npQCD deconfined QGP, at certain characteristic temperature thresholds.

• 2. Suppression of dijets which arise from primordial $q\overline {q}$ pair production fragmenting into partonic showers (jets) in vacuum but being attenuated by QGP-medium induced gluonic bremsstrahlung: Jet quenching in A+A collisions.

  • a. A variant of this: any primordial hard parton suffers a high, specific loss of energy when traversing a deconfined medium: High p _T suppression in A+A collisions.

• 3. Hydrodynamic collective motion develops with the onset of (local) thermal equilibrium. It is created by partonic pressure gradients that reflect the initial collisional impact geometry via non-isotropies in particle emission called “directed” and “elliptic” flow. The latter reveals properties of the QGP, seen here as an ideal partonic fluid.

  • a. Radial hydrodynamical expansion flow (“Hubble expansion”) is a variant of the above that occurs in central, head on collisions with cylinder symmetry, as a consequence of an isentropic expansion. It should be sensitive to the mixed phase conditions characteristic of a first order parton-hadron phase transition.

• 4. Hadronic “chemical” freeze-out fixes the abundance ratios of the hadronic species into an equilibrium distribution. Occurring very close to, or at hadronization, it reveals the dynamical evolution path in the [T, μ _B] plane and determines the critical temperature and density of QCD. The yield distributions in A+A collisions show a dramatic strangeness enhancement effect, characteristic of an extended QCD medium.

• 5. Fluctuations, from one collision event to another (and even within a single given event) can be quantified in A+A collisions due to the high charged hadron multiplicity density (of up to 600 per rapidity unit at top RHIC energy). Such event-by-event (Debye) fluctuations of pion rapidity density and mean transverse momentum (event “temperature”), as well as event-wise fluctuations of the strange to non-strange hadron abundance ratio (may) reflect the existence and position of the conjectured critical point of QCD (Fig. 7.1).

• 6. Two particle Bose-Einstein-Correlations are the analog of the Hanbury-Brown, Twiss (HBT) effect of quantum optics. They result from the last interaction experienced by hadrons, i.e. from the global decoupling stage. Owing to a near isentropic hadronic expansion they reveal information on the overall space-time-development of the “fireball” evolution.

In an overall view the first group of observables (1 to 2a) is anchored in established pQCD physics that is well known from theoretical and experimental analysis of elementary collisions (e ⁺e ⁻ annihilation, pp and $p\overline {p}$ data). In fact, the first generation of high Q ² baryon collisions, occurring at the microscopic level in A+A collisions, should closely resemble such processes. However, their primary partonic products do not escape into pQCD vacuum but get attenuated by interaction with the concurrently developing extended high density medium, thus serving as diagnostic tracer probes of that state. The remaining observables capture snapshots of the bulk matter medium itself. After initial equilibration we may confront elliptic flow data with QCD during the corresponding partonic phase of the dynamical evolution employing thermodynamic [21] and hydrodynamic [22] models of a high temperature parton plasma. The hydro-model stays applicable well into the hadronic phase. Hadron formation (confinement) occurs in between these phases (at about 5 μs time in the cosmological evolution). In fact relativistic nuclear collision data may help to finally pin down the mechanism(s) of this fascinating QCD process [23,24,25] as we can vary the conditions of its occurrence, along the parton-hadron phase separation line of Fig. 7.1, by proper choice of collisional energy $\sqrt {s}$, and system size A, while maintaining the overall conditions of an extended imbedding medium of high energy density within which various patterns [9,10,11, 15, 16] of the hadronization phase transition may establish. The remaining physics observables (3a, 5 and 6 above) essentially provide for auxiliary information about the bulk matter system as it traverses (and emerges from) the hadronization stage, with special emphasis placed on manifestations of the conjectured critical point.

The present review will briefly cover each of the above physics observables in a separate chapter, beginning with the phenomena of confinement and hadronization (Sect. 7.3), then to turn to the preceding primordial dynamics, e.g. to elliptical flow (Sect. 7.4), high p _T and jet quenching (Sect. 7.5) and quarkonium suppression (Sect. 7.6) as well as in-medium ϱ-meson “melting”. We then turn to the late period, with correlation and fluctuation studies (Sect. 7.7). We conclude (Sect. 7.8) with a summary, including an outlook to the future of the research field.

However, before turning to such specific observables we shall continue this introductory chapter, with a look at the origin, and earlier development of the ideas that have shaped this field of research (Sect. 7.1.2). Then we turn to a detailed description of the overall dynamical evolution of relativistic nucleus-nucleus collisions, and to the typical overall patterns governing the final distributions in transverse and longitudinal (rapidity) phase space (Sect. 7.2). The aspects of an approach toward equilibrium, at various stages of the dynamical evolution (which are of key importance toward the intended elucidation of the QCD matter phase diagram), will be considered, in particular.

7.1.2 History

The search for the phase diagram of strongly interacting matter arose in the 1960s, from a coincidence of ideas developing—at first fairly independently—in nuclear and astrophysics. In fact, the nuclear proton-neutron matter, a quantum liquid at T = 0 and energy density 𝜖 = 0.15 GeV/fm³, represents the ground state of extended QCD matter. Of course, QCD was unknown during the development of traditional nuclear physics, and the extended matter aspects of nuclei—such as compressibility or the equation of state, in general—did not receive much attention until the advent, in the 1960s, of relativistic nuclear mean field theory, notably s-matrix theory by Brueckner [26] and the σ-model of Walecka [27]. These theories developed the novel view of “infinite nuclear matter” structure, based on in-medium properties of the constituent baryons that share parts of their vacuum mass and surface structure with the surrounding, continuous field of relativistic scalar and vector mesons. Most importantly, in the light of subsequent development, these theories allowed for a generalization away from ground state density and zero temperature. Such developments turned out to be of key relevance for acute nuclear astrophysics problems: the dynamics of type II super-novae and the stability of neutron stars, which both required the relation of pressure to density and temperature of hadronic matter, i.e. the hadronic matter equation of state (EOS). H.A. Bethe et al. [28] postulated that the final stages of supernova collapse should evolve through the density interval 0.1 ≤ ϱ∕ϱ ₀ ≤ 5 where ϱ ₀ = 0.16 (baryons per fm³) is the nuclear matter ground state density, and a similar domain was expected for the neutron star density variation from surface to interior [29]. It was clear that, at the highest thus considered densities the EOS might soften due to strange hadron production caused by increasing Fermi energy. However the field theoretical models permitted no reliable extrapolation to such high densities (which, in retrospect, are perhaps not reached in supernova dynamics [30]), and the experimental information concerning the EOS from study of the giant monopole resonance—a collective density oscillation also called “breathing mode”—covered only the parabolic minimum occurring in the related function of energy vs. density at T = 0, ϱ = ϱ ₀.

The situation changed around 1970 due to the prediction made by W. Greiner et al. [31] that nucleus-nucleus collisions, at relatively modest relativistic energies, would result in shock compression. This mechanism promised to reach matter densities far beyond those of a mere superposition (i.e. ϱ∕ϱ ₀ ≤ 2γ) of initial target and projectile densities. Coinciding in time, the newly developed Bevalac accelerator at LBL Berkeley offered projectiles up to ³⁸Ar, at just the required energies, 100 MeV ≤ E _Lab∕nucleon ≤ 2 GeV. The field of “relativistic heavy ion physics” was born. The topic was confronted, at first, with experimental methods available both from nuclear and particle physics. It was shown that particle production (here still restricted to pions and kaons) could indeed be linked to the equation of state [32] and that, even more spectacularly, the entire “fireball” of mutually stopped hadrons developed decay modes very closely resembling the initial predictions of hydrodynamical shock flow modes [33] which directly link primordial pressure gradients with collective velocity fields of matter streaming out, again governed by the nuclear/hadronic matter EOS. Actually, both these statements do, in fact, apply (mutatis mutandis) up to the present ultra-relativistic energies (see Sects. 7.2–7.4). However it turned out soon that the equation of state at low or even zero temperature (as required in supernova and neutron star studies) could only be obtained in a semi-empirical manner [34]. The reason: compression can, in such collisions, be only accomplished along with temperature and entropy increase. In an ideal baryon gas $\exp (s/A) \propto T^{3/2}/\varrho$, i.e. T ^3∕2 will grow faster than ϱ in a non-isentropic compression. Thus the reaction dynamics will be sensitive to various isothermes of the ground state EOS P = f(ϱ, T = 0), staying at T ≫ 0, throughout, and, moreover, not at constant T. Thus a relativistic dynamical mean field model is required in order to interactively deduce the T = 0 EOS from data [34]. The EOS result thus remains model dependent.

The ideas concerning creation of a quark gluon plasma arose almost concurrent with the heavy ion shock compression proposal. In 1974 T.D. Lee formulated the idea that the non-perturbative vacuum condensates could be “melted down …by distributing high energy or high nucleon density over a relatively large volume” [35]. Collins and Perry [36] realized that the asymptotic freedom property of QCD implies the existence of an ultra-hot form of matter with deconfined quarks and gluons, an idea that gained wide recognition when S. Weinberg [37] proposed an asymptotic freedom phase at the beginning of “The first Three minutes”. In fact, this idea of deconfinement by asymptotic freedom (with implied temperature of several GeV) was correct, but somewhat besides the point, as everybody expected, likewise, that deconfinement sets in right above the limiting hadron temperature of R. Hagedorn [38], T _H ≈ 160 MeV. A medium existing down to that temperature would, however, feature an average momentum square transfer Q ² < 1 GeV², i.e. be far into the non perturbative domain, and very far from asymptotic freedom. Right above the hadron to parton transition the “quark gluon plasma” (as it was named by E. Shuryak [39]) is not a weakly coupled ideal pQCD gas as soon became obvious by Lattice QCD calculations for extended matter [40]. Seen in retrospect one obviously cannot defend a picture of point like quarks (with “current” masses) at Q ² ≤ 0.2 GeV² where size scales of 0.5 to 1 fm must play a dominating role.

An analytic QCD description of deconfinement does not exist. For heavy quarkonia, $c \overline {c} \: (J/\Psi )$ and $b \overline {b} \: (Y)$ deconfinement in partonic matter, Matsui and Satz proposed [41] a Debye screening mechanism, caused by the high spatial density of free color carriers, that removes the confining long range potential as T increases toward about 2 T _c, an effect reproduced by modern lattice QCD [42]. However, light hadron deconfinement cannot be understood with a non-relativistic potential model. Such critical remarks not withstanding, we shall demonstrate in Sects. 7.3–7.6 that the very existence, and also crucial properties of the QGP can in fact be inferred from experiment, and be confronted with corresponding predictions of recent lattice QCD theory.

Our present level of an initial understanding of the phase diagram of QCD matter (Fig. 7.1), is the result of a steady development of both experiment and theory, that began about three decades ago, deriving initial momentum from the Bevalac physics at LBL which motivated—along with the developing formulation of the quark gluon plasma research goals—a succession of experimental facilities progressing toward higher $\sqrt {s}$. Beginning with the AGS at BNL (²⁸Si and ¹⁹⁷Au beams with $\sqrt {s} \le 5$ GeV), the next steps were taken at the CERN SPS ($\sqrt {s}$ from 6 to 20 GeV; ¹⁶O, ³²S, ²⁰⁸Pb beams), and at the Relativistic Heavy Ion Collider RHIC (the first facility constructed explicitly for nuclear collisions) which offers beams of ⁶⁴Cu and ¹⁹⁷Au at $20 \le \sqrt {s} \le 200$ GeV. A final, gigantic step in energy will be taken 2008 with the CERN Large Hadron Collider: ²⁰⁸Pb beams at $\sqrt {s}= 5.5$ TeV.

7.2 Bulk Hadron Production in A+A Collisions

In this section we take an overall look at bulk hadron production in nucleus-nucleus collisions. In view of the high total c.m. energies involved at e.g. top SPS $(E^{\text{tot}}_{\text{cm}} \approx 3.3$ TeV) and top RHIC (38 TeV) energies, in central Pb+Pb (SPS) and Au+Au (RHIC) collisions, one can expect an extraordinarily high spatial density of produced particles. Thus, as an overall idea of analysis, one will try to relate the observed flow of energy into transverse and longitudinal phase space and particle species to the high energy density contained in the primordial interaction volume, thus to infer about its contained matter. The typical experimental patterns of such collisions, both in collider mode at RHIC and in a fixed target configuration at the SPS, are illustrated in Fig. 7.2 which shows a fractional view of the total distribution of charged particles (about 4000 and 1600, respectively) within the tracking volume of the STAR and NA49 experiments.

Fig. 7.2

Charged particle tracks in central Au+Au and Pb+Pb collision events, in collider geometry (top) from RHIC STAR TPC tracking at $\sqrt {s}=200$ GeV, and in fixed target geometry (bottom) from NA49 at the SPS, $\sqrt {s}=17.3$ GeV

Most of these tracks correspond to “thermal” pions (p _T up to 2 GeV) and, in general, such thermal hadrons make up for about 95% of the observed multiplicity: the bulk of hadron production. Their distributions in phase space will be illustrated in the subsections below. This will lead to a first insight into the overall reaction dynamics, and also set the stage for consideration of the rare signals, imbedded in this thermal bulk production: correlations, jets, heavy flavors, fluctuations, which are the subject of later chapters.

7.2.1 Particle Multiplicity and Transverse Energy Density

Particle production can be assessed globally by the total created transverse energy, the overall result of the collisional creation of transverse momentum p _T or transverse mass ($m_{\mathrm {T}}=\sqrt { p^2_{\mathrm {T}} + m^2_0}$), at the microscopic level. Figure 7.3 shows the distribution of total transverse energy $E_{\mathrm {T}}=\sum \limits _i \: E(\Theta _i) \cdot \sin \Theta$ resulting from a calorimetric measurement of energy flow into calorimeter cells centered at angle Θ_i relative to the beam [43], for ³²S + ¹⁹⁷Au collisions at $\sqrt {s} = 20$ GeV, and for ²⁰⁸Pb + ²⁰⁸Pb collisions at $\sqrt {s} = 17.3$ GeV.

Fig. 7.3

Minimum bias distribution of total transverse energy in Pb+Pb collisions at $\sqrt {s}=17.3$ GeV, and S+Au collisions at $\sqrt {s}=20$ GeV, in the rapidity interval 2.1 < y < 3.4, from [43]

The shape is characteristic of the impact parameter probability distribution (for equal size spheres in the Pb+Pb case). The turnoff at E _T = 520 GeV indicates the point where geometry runs out of steam, i.e. where b → 0, a configuration generally referred to as a “central collision”. The adjacent shoulder results from genuine event by event fluctuations of the actual number of participant nucleons from target and projectile (recall the diffuse Woods-Saxon nuclear density profiles), and from experimental factors like calorimeter resolution and limited acceptance. The latter covers 1.3 units of pseudo-rapidity and contains mid-rapidity η _mid = 2.9. Re-normalizing [43] to Δ η = 1 leads to dE _T∕dη (mid) = 400 GeV, in agreement with the corresponding WA80 result [44]. Also, the total transverse energy of central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV turns out to be about 1.2 TeV. As the definition of a central collision, indicated in Fig. 7.3, can be shown [42] to correspond to an average nucleon participant number of N _part = 370 one finds an average total transverse energy per nucleon pair, of $E_{\mathrm {T}}/\left <0.5 \: N_{\text{part}}\right >=6.5$ GeV. After proper consideration of the baryon pair rest mass (not contained in the calorimetric E _T response but in the corresponding $\sqrt {s}$) one concludes [43] that the observed total E _T corresponds to about $0.6 \; E_{\mathrm {T}}^{\max }$, the maximal E _T derived from a situation of “complete stopping” in which the incident $\sqrt {s}$ gets fully transformed into internal excitation of a single, ideal isotropic fireball located at mid-rapidity. The remaining fraction of $E_{\mathrm {T}}^{\max }$ thus stays in longitudinal motion, reflecting the onset, at SPS energy, of a transition from a central fireball to a longitudinally extended “fire-tube”, i.e. a cylindrical volume of high primordial energy density. In the limit of much higher $\sqrt {s}$ one may extrapolate to the idealization of a boost invariant primordial interaction volume, introduced by Bjorken [45].

We shall show below (Sect. 7.2.2) that the charged particle rapidity distributions, from top SPS to top RHIC energies, do in fact substantiate a development toward a boost-invariant situation. One may thus employ the Bjorken model for an estimate of the primordial spatial energy density 𝜖, related to the energy density in rapidity space via the relation [45]

$$\displaystyle \begin{aligned} \epsilon(\tau_0) = \frac{1}{\pi R^2} \: \frac{1}{\tau_0} \: \frac{\mathrm{d} E_{\mathrm{T}}}{\mathrm{d} y} {}\end{aligned} $$

(7.1)

where the initially produced collision volume is considered as a cylinder of length dz = τ ₀ dy and transverse radius R ∝ A ^1∕3. Inserting for πR ² the longitudinally projected overlap area of Pb nuclei colliding near head-on (“centrally”), and assuming that the evolution of primordial pQCD shower multiplication (i.e. the energy transformation into internal degrees of freedom) proceeds at a time scale τ ₀ ≤ 1 fm/c, the above average transverse energy density, of dE _T∕dy = 400 GeV at top SPS energy [43, 44] leads to the estimate

$$\displaystyle \begin{aligned} \epsilon (\tau_0=1 \: \ \text{fm})=3.0 \pm 0.6 \: \ \text{GeV/fm}^3, {} \end{aligned} $$

(7.2)

thus exceeding, by far, the estimate of the critical energy density 𝜖 ₀ obtained from lattice QCD (see below), of about 1.0 GeV/fm³. Increasing the collision energy to $\sqrt {s}=200$ GeV for Au+Au at RHIC, and keeping the same formation time, τ ₀ = 1 fm/c (a conservative estimate as we shall show in Sect. 7.2.4), the Bjorken estimate grows to 𝜖 ≈ 6.0 ± 1 GeV/fm³. This statement is based on the increase of charged particle multiplicity density at mid-rapidity with $\sqrt {s}$, as illustrated in Fig. 7.4. From top SPS to top RHIC energy [46] the density per participant nucleon pair almost doubles. However, at $\sqrt {s}=200$ GeV the formation or thermalization time τ ₀, employed in the Bjorken model [45], was argued [47] to be shorter by a factor of about 4. We will return to such estimates of τ ₀ in Sect. 7.2.5 but note, for now, that the above choice of τ ₀ = 1 fm/c represents a conservative upper limit at RHIC energy.

Fig. 7.4

Charged hadron rapidity density at mid-rapidity vs. $\sqrt {s}$, compiled from $e^+e^-, \: pp, \: p \overline {p}$ and A+A collisions [53]

These Bjorken-estimates of spatial transverse energy density are confronted in Fig. 7.5 with lattice QCD results obtained for three dynamical light quark flavors [48], and for zero baryo-chemical potential (as is realistic for RHIC energy and beyond but still remains a fair approximation at top SPS energy where μ _B ≈ 250 MeV). The energy density of an ideal, relativistic parton gas scales with the fourth power of the temperature,

$$\displaystyle \begin{aligned} \epsilon = gT^4 {} \end{aligned} $$

(7.3)

where g is related to the number of degrees of freedom. For an ideal gluon gas, g = 16 π ²∕30; in an interacting system the effective g is smaller. The results of Fig. 7.5

Fig. 7.5

Lattice QCD results at zero baryon potential for energy density 𝜖∕T ⁴ versus T∕T _c with three light quark flavors, compared to the Stefan-Boltzmann-limit 𝜖 _SB of an ideal quark-gluon gas [48]

show, in fact, that the Stefan-Boltzmann limit 𝜖 _SB is not reached, due to non perturbative effects, even at four times the critical temperature T _c = 170 MeV. The density 𝜖∕T ⁴ = g is seen to ascend steeply, within the interval T _c ± 25 MeV. At T _c the critical QCD energy density 𝜖 = 0.6–1.0 GeV/fm³. Relating the thermal energy density with the Bjorken estimates discussed above, one arrives at an estimate of the initial temperatures reached in nucleus-nucleus collisions, thus implying thermal partonic equilibrium to be accomplished at time scale τ ₀ (see Sect. 7.2.5). For the SPS, RHIC and LHC energy domains this gives an initial temperature in the range 190 ≤ T ^SPS ≤ 220 MeV, 220 ≤ T ^RHIC ≤ 400 MeV (assuming [47] that τ ₀ decreases to about 0.3 fm/c here) and T ^LHC ≥ 600 MeV, respectively. From such estimates one tends to conclude that the immediate vicinity of the phase transformation is sampled at SPS energy, whereas the dynamical evolution at RHIC and LHC energies dives deeply into the “quark-gluon-plasma” domain of QCD. We shall return to a more critical discussion of such ascertations in Sect. 7.2.5.

One further aspect of the mid-rapidity charged particle densities per participant pair requires attention: the comparison with data from elementary collisions. Figure 7.4 shows a compilation of $pp, \: p\overline {p}$ and e ⁺e ⁻ data covering the range from ISR to LEP and Tevatron energies.

The data from e ⁺e ⁻ represent dN _ch∕dy, the rapidity density along the event thrust axis, calculated assuming the pion mass [49] (the difference between dN∕dy and dN∕dη can be ignored here). Remarkably, they superimpose with the central A+A collision data, whereas pp and $p\overline {p}$ show similar slope but amount to only about 60% of the AA and e ⁺e ⁻ values. This difference between e ⁺e ⁻ annihilation to hadrons, and pp or $p\overline {p}$ hadro-production has been ascribed [50] to the characteristic leading particle effect of minimum bias hadron-hadron collisions which is absent in e ⁺e ⁻. It thus appears to be reduced in AA collisions due to subsequent interaction of the leading parton with the oncoming thickness of the remaining target/projectile density distribution. This naturally leads to the scaling of total particle production with N _part that is illustrated in Fig. 7.6,

Fig. 7.6

The total number of charged hadrons per participant pair shown as a function of N _part in Au+Au collisions at three RHIC energies [53]

for three RHIC energies and minimum bias Au+Au collisions; the close agreement with e ⁺e ⁻ annihilation data is obvious again. One might conclude that, analogously, the participating nucleons get “annihilated” at high $\sqrt {s}$, their net quantum number content being spread out over phase space (as we shall show in the next section).

7.2.2 Rapidity Distributions

Particle production number in A+A collisions depends globally on $\sqrt {s}$ and collision centrality, and differentially on p _T and rapidity y, for each particle species i. Integrating over p _T results in the rapidity distribution dN _i∕dy. Particle rapidity,¹y = sinh⁻¹p _L∕M _T (where $M_{\mathrm {T}}=\sqrt {m^2 + p_{\mathrm {T}}^2}$), requires mass identification. If that is unknown one employs pseudo-rapidity ($\eta = - \ln \: [\mbox{tan}(\Theta /2)]$) instead. This is also chosen if the joint rapidity distribution of several unresolved particle species is considered: notably the charged hadron distribution. We show two examples in Fig. 7.7. The left panel illustrates charged particle production in $p\overline {p}$ collisions studied by UA1 at $\sqrt {s}=540$ GeV [51]. Whereas the minimum bias distribution (dots) exhibits the required symmetry about the center of mass coordinate, η = 0, the rapidity distribution corresponding to events in which a W boson was produced (histogram) features, both, a higher average charged particle yield, and an asymmetric shape. The former effect can be seen to reflect the expectation that the W production rate increases with the “centrality” of $p\overline {p}$ collisions, involving more primordial partons as the collisional overlap of the partonic density profiles gets larger, thus also increasing the overall, softer hadro-production rate. The asymmetry should result from a detector bias favoring W identification at negative rapidity: the transverse W energy, of about 100 GeV would locally deplete the energy store available for associated soft production. If correct, this interpretation suggests that the wide rapidity gap between target and projectile, arising at such high $\sqrt {s}$, of width $\Delta y \approx 2 \: \ln \:(2 \gamma _{\text{CM}})$, makes it possible to define local sub-intervals of rapidity within which the species composition of produced particles varies.

Fig. 7.7

Left panel: charged particle pseudo-rapidity distribution in $p \overline {p}$ collisions at $\sqrt {s}=540$ GeV [51]. Right panel: same in RHIC Au+Au collisions at $\sqrt {s}=130$ GeV at different centralities [52]. Closed lines represent fits with the color glass condensate model [64]

Fig. 7.8

Pseudo-rapidity distribution of charged hadrons produced in central Au+Au collisions at $\sqrt {s}=200$ GeV compared with e ⁺e ⁻ data at similar energy. The former data normalized by N _part∕2. From ref. [53]

Fig. 7.9

Left panel: negative pion rapidity distributions in central Au+Au and Pb+Pb collisions from AGS via SPS to RHIC energies [54]. Right panel: the Gaussian rapidity width of pions versus $\sqrt {s}$, confronted by Landau model predictions (solid line) [54]

Fig. 7.10

Net proton rapidity distributions in central Au+Au/Pb+Pb collisions at AGS, SPS and RHIC energies [56, 57]

The right panel of Fig. 7.7 shows charged particle pseudo-rapidity density distributions for Au+Au collisions at $\sqrt {s}=130$ GeV measured by RHIC experiment PHOBOS [52] at three different collision centralities, from “central” (the 6% highest charged particle multiplicity events) to semi-peripheral (the corresponding 35–45% cut). We will turn to centrality selection in more detail below. Let us first remark that the slight dip at mid-rapidity and, moreover, the distribution shape in general, are common to $p\overline {p}$ and Au+Au. This is also the case for e ⁺e ⁻ annihilation as is shown in Fig. 7.8 which compares the ALEPH rapidity distribution along the mean p _T (“thrust”) axis of jet production in e ⁺e ⁻ at $\sqrt {s}=200$ GeV [49] with the scaled PHOBOS-RHIC distribution of central Au+Au at the same $\sqrt {s}$ [53]. Note that the mid-rapidity values contained in Figs. 7.7 and 7.8 have been employed already in Fig. 7.4, which showed the overall $\sqrt {s}$ dependence of mid-rapidity charged particle production. What we concluded there was a perfect scaling of A+A with e ⁺e ⁻ data at $\sqrt {s} \ge 20$ GeV and a 40% suppression of the corresponding $pp, \: p\overline {p}$ yields. We see here that this observation holds, semi-quantitatively, for the entire rapidity distributions. These are not ideally boost invariant at the energies considered here but one sees in dN _ch∕dy a relatively smooth “plateau” region extending over ∣y∣ ≤ 1.5–2.5.

The production spectrum of charged hadrons is, by far, dominated by soft pions (p _T ≤ 1 GeV/c) which contribute about 85% of the total yield, both in elementary and nuclear collisions. The evolution of the π ⁻ rapidity distribution with $\sqrt {s}$ is illustrated in Fig. 7.9 for central Au+Au and Pb+Pb collisions from AGS via SPS to RHIC energy, $2.7 \le \sqrt {s} \le 200$ GeV [54].

At lower $\sqrt {s}$ the distributions are well described by single Gaussian fits [54] with σ(y) nearly linearly proportional to the total rapidity gap $\Delta y \propto \: \ln \sqrt {s}$ as shown in the right hand panel of Fig. 7.9. Also illustrated is the prediction of the schematic hydrodynamical model proposed by Landau [55],

$$\displaystyle \begin{aligned} \sigma^2 \propto \ln \: \left( \frac{\sqrt{s}}{2m_p} \right) {} \end{aligned} $$

(7.4)

which pictures hadron production in high $\sqrt {s}$pp collisions to proceed via a dynamics of initial complete “stopping down” of the reactants matter/energy content in a mid-rapidity fireball that would then expand via 1-dimensional ideal hydrodynamics. Remarkably, this model that has always been considered a wildly extremal proposal falls rather close to the lower $\sqrt {s}$ data for central A+A collisions but, as longitudinal phase space widens approaching boost invariance we expect that the (non-Gaussian) width of the rapidity distribution grows linearly with the rapidity gap Δy. LHC data will finally confirm this expectation, but Figs. 7.7, 7.8, and 7.9 clearly show the advent of boost invariance, already at $\sqrt {s} = 200$ GeV.

A short didactic aside: At low $\sqrt {s}$ the total rapidity gap Δy = 2–3 does closely resemble the total rapidity width obtained for a thermal pion velocity distribution at temperature T = 120–150 MeV, of a single mid-rapidity fireball, the y-distribution of which represents the longitudinal component according to the relation [19]

$$\displaystyle \begin{aligned} \frac{{\mathrm{d}} N}{{\mathrm{d}} y} \propto \left( m^2T \:+ \frac{2mT^2}{\text{cosh} \, y} \: + \frac{2T^2}{\text{cosh}^2y} \right) \: \exp \: [-m \; \mbox{cosh} \, y/T] {} \end{aligned} $$

(7.5)

where m is the pion mass. Any model of preferentially longitudinal expansion of the pion emitting source, away from a trivial single central “completely stopped” fireball, can be significantly tested only once Δy > 3 which occurs upward from SPS energy. The agreement of the Landau model prediction with the data in Fig. 7.9 is thus fortuitous, below $\sqrt {s} \approx 10$ GeV, as any created fireball occupies the entire rapidity gap with pions.

The Landau model offers an extreme view of the mechanism of “stopping”, by which the initial longitudinal energy of the projectile partons or nucleons is inelastically transferred to produced particles and redistributed in transverse and longitudinal phase space, of which we saw the total transverse fraction in Fig. 7.3. Obviously e ⁺e ⁻ annihilation to hadrons represents the extreme stopping situation. Hadronic and nuclear collisions offer the possibility to analyze the final distribution in phase space of their non-zero net quantum numbers, notably net baryon number. Figure 7.10

shows the net-proton rapidity distribution (i.e. the proton rapidity distribution subtracted by the antiproton distribution) for central Pb+Pb/Au+Au collisions at AGS ($\sqrt {s}=5.5$ GeV), SPS ($\sqrt {s} \le 17.3$ GeV) and RHIC ($\sqrt {s}=200$ GeV) [56]. With increasing energy we see a central (but non-Gaussian) peak developing into a double-hump structure that widens toward RHIC leaving a plateau about mid-rapidity. The RHIC-BRAHMS experiment acceptance for $p, \: \overline {p}$ identification does unfortunately not reach up to the beam fragmentation domain at y _p = 5.4 (nor does any other RHIC experiment) but only to y ≈ 3.2, with the consequence that the major fraction of p ^net is not accounted for. However the mid-rapidity region is by no means net baryon free. At SPS energy the NA49 acceptance covers the major part of the total rapidity gap, and we observe in detail a net p distribution shifted down from y _p = 2.9 by an average rapidity shift [56] of $\left <\delta y\right > = 1.7$. From Fig. 7.10 we infer that $\left <\delta y\right >$ cannot scale linearly with $y_p \approx \ln (2\gamma _{\text{CM}}) \approx \ln \sqrt {s}$ for ever—as it does up to top SPS energy where $\left <\delta y\right >=0.58 \: y_p$ [56]. Because extrapolating this relation to $\sqrt {s}=200$ GeV would result in $\left <\delta y\right >=3.1$, and with y _p ≈ 5.4 at this energy we would expect to observe a major fraction of net proton yield in the vicinity of y = 2.3 which is not the case. A saturation must thus occur in the $\left <\delta y\right >$ vs. $\sqrt {s}$ dependence.

The re-distribution of net baryon density over longitudinal phase space is, of course, only partially captured by the net proton yield but a recent study [57] has shown that proper inclusion of neutron² and hyperon production data at SPS and RHIC energy scales up, of course, the dN∕dy distributions of Fig. 7.10 but leaves the peculiarities of their shapes essentially unchanged. As the net baryon rapidity density distribution should resemble the final valence quark distribution the Landau model is ruled out as the valence quarks are seen to be streaming from their initial position at beam rapidity toward mid-rapidity (not vice versa). It is remarkable, however, to see that some fraction gets transported very far, during the primordial partonic non-equilibrium phase. We shall turn to its theoretical description in Sect. 7.2.4 but note, for now, that pp collisions studied at the CERN ISR [58] lead to a qualitatively similar net baryon rapidity distribution, albeit characterized by a smaller $\left <\delta y\right >$.

The data described above suggest that the stopping mechanism universally resides in the primordial, first generation of collisions at the microscopic level. The rapidity distributions of charged particle multiplicity, transverse energy and valence quark exhibit qualitatively similar shapes (which also evolve similarly with $\sqrt {s}$) in $pp, \: p\overline {p}, \: e^+e^-$ reactions, on the one hand, and in central or semi-peripheral collisions of A ≈ 200 nuclei, on the other. Comparing in detail we formulate a nuclear modification factor for the bulk hadron rapidity distributions,

$$\displaystyle \begin{aligned} R^{\text{AA}}_y \: \equiv \: \frac{{\mathrm{d}} N^{\text{ch}}/{\mathrm{d}} y \: (y) \quad \mbox{in A+A}}{0.5 \: N_{\text{part}} \:\: {\mathrm{d}} N^{\text{ch}}/{\mathrm{d}} y \quad \mbox{in pp}} {} \end{aligned} $$

(7.6)

where N _part < 2A is the mean number of “participating nucleons” (which undergo at least one inelastic collision with another nucleon) which increases with collision centrality. For identical nuclei colliding $\left <N^{\text{proj}}_{\text{part}}\right >\simeq \left <N^{\text{targ}}_{\text{part}}\right >$ and thus 0.5 N _part gives the number of opposing nucleon pairs. R ^AA = 1 if each such “opposing” pair contributes the same fraction to the total A+A yield as is produced in minimum bias pp at similar $\sqrt {s}$. From Figs. 7.4 and 7.6 we infer that for ∣η∣ < 1, R ^AA = 1.5 at top RHIC energy, and for the pseudo-rapidity integrated total N ^ch we find R ^AA = 1.36, in central Au+Au collisions. AA collisions thus provide for a higher stopping power than pp (which is also reflected in the higher rapidity shift $\left <\delta y\right >$ of Fig. 7.10). The observation that their stopping power resembles the e ⁺e ⁻ inelasticity suggests a substantially reduced leading particle effect in central collisions of heavy nuclei. This might not be surprising. In a Glauber-view of successive minimum bias nucleon collisions occurring during interpenetration, each participating nucleon is struck ν > 3 times on average, which might saturate the possible inelasticity, removing the leading fragment.

This view naturally leads to the scaling of the total particle production in nuclear collisions with N _part, as seen clearly in Fig. 7.6, reminiscent of the “wounded nucleon model” [59] but with the scaling factor determined by e ⁺e ⁻ rather than pp [60]. Overall we conclude from the still rather close similarity between nuclear and elementary collisions that the mechanisms of longitudinal phase space population occur primordially, during interpenetration which is over after 0.15 fm/c at RHIC, and after 1.5 fm/c at SPS energy. I.e. it is the primordial non-equilibrium pQCD shower evolution that accounts for stopping, and its time extent should be a lower limit to the formation time τ ₀ employed in the Bjorken model [45], Eq. (7.1). Equilibration at the partonic level might begin at t > τ ₀ only (the development toward a quark-gluon-plasma phase), but the primordial parton redistribution processes set the stage for this phase, and control the relaxation time scales involved in equilibration [61]. More about this in Sect. 7.2.5. We infer the existence of a saturation scale [62] controlling the total inelasticity: with ever higher reactant thickness, proportional to A ^1∕3, one does not get a total rapidity or energy density proportional to A ^4∕3 (the number of “successive binary collisions”) but to A ^1.08 only [63]. Note that the lines shown in Fig. 7.7 (right panel) refer to such a saturation theory: the color glass condensate (CGC) model [64] developed by McLerran and Venugopulan. The success of these models demonstrates that “successive binary baryon scattering” is not an appropriate picture at high $\sqrt {s}$. One can free the partons from the nucleonic parton density distributions only once, and their corresponding transverse areal density sets the stage for the ensuing QCD parton shower evolution [62]. Moreover, an additional saturation effect appears to modify this evolution at high transverse areal parton density (see Sect. 7.2.4).

7.2.3 Dependence on System Size

We have discussed above a first attempt toward a variable (N _part) that scales the system size dependence in A+A collisions. Note that one can vary the size either by centrally colliding a sequence of nuclei, A₁ + A₁, A₂ + A₂ etc., or by selecting different windows in N _part out of minimum bias collision ensembles obtained for heavy nuclei for which BNL employs ¹⁹⁷Au and CERN ²⁰⁸Pb. The third alternative, scattering a relatively light projectile, such as ³²S, from increasing A nuclear targets, has been employed initially both at the AGS and SPS but got disfavored in view of numerous disadvantages, of both experimental (the need to measure the entire rapidity distribution, i.e. lab momenta from about 0.3–100 GeV/c, with uniform efficiency) and theoretical nature (different density distributions of projectile and target; occurrence of an “effective” center of mass, different for hard and soft collisions, and depending on impact parameter).

The determination of N _part is of central interest, and thus we need to look at technicalities, briefly. The approximate linear scaling with N _part that we observed in the total transverse energy and the total charged particle number (Figs. 7.3 and 7.6) is a reflection of the primordial redistribution of partons and energy. Whereas all observable properties that refer to the system evolution at later times, which are of interest as potential signals from the equilibrium, QCD plasma “matter” phase, have different specific dependences on N _part, be it suppressions (high p _T signals, jets, quarkonia production) or enhancements (collective hydrodynamic flow, strangeness production). N _part thus emerges as a suitable common reference scale.

N _part captures the number of potentially directly hit nucleons. It is estimated from an eikonal straight trajectory Glauber model as applied to the overlap region arising, in dependence of impact parameter b, from the superposition along beam direction of the two initial Woods-Saxon density distributions of the interacting nuclei. To account for the dilute surfaces of these distributions (within which the intersecting nucleons might not find an interaction partner) each incident nucleon trajectory gets equipped with a transverse radius that represents the total inelastic NN cross section at the corresponding $\sqrt {s}$. The formalism is imbedded into a Monte Carlo simulation (for detail see [66]) starting from random microscopic nucleon positions within the transversely projected initial Woods-Saxon density profiles. Overlapping cross sectional tubes of target and projectile nucleons are counted as a participant nucleon pair. Owing to the statistics of nucleon initial position sampling each considered impact parameter geometry thus results in a probability distribution of derived N _part. Its width σ defines the resolution Δ(b) of impact parameter b determination within this scheme via the relation

$$\displaystyle \begin{aligned} \frac{1}{\Delta (b)} \: \sigma (b) \approx \frac{{\mathrm{d}}\left<N_{\text{part}}(b)\right>}{{\mathrm{d}}b} {} \end{aligned} $$

(7.7)

which, at A = 200, leads to the expectation to determine b with about 1.5 fm resolution [66], by measuring N _part.

How to measure N _part? In fixed target experiments one can calorimetrically count all particles with beam momentum per nucleon and superimposed Fermi momentum distributions of nucleons, i.e. one looks for particles in the beam fragmentation domain y _beam ± 0.5, p _T ≤ 0.25 GeV/c. These are identified as spectator nucleons, and $N^{\text{proj}}_{\text{part}}=A-N^{\text{proj}}_{\text{spec}}$. For identical nuclear collision systems $\left <N_{\text{part}}^{\text{proj}}\right >= \left <N_{\text{part}}^{\text{targ}}\right >$, and thus N _part gets approximated by $2 N_{\text{part}}^{\text{proj}}$. This scheme was employed in the CERN experiments NA49 and WA80, and generalized [67] in a way that is illustrated in Fig. 7.11.

Fig. 7.11

(a) Energy spectrum of the forward calorimeter in Pb+Pb collisions at 158A GeV; (b) impact parameter and fraction of total inelastic cross section related to forward energy from the VENUS model [67, 68]

The top panel shows the minimum bias distribution of total energy registered in a forward calorimeter that covers the beam fragment domain in Pb+Pb collisions at lab. energy of 158 GeV per projectile nucleon, $\sqrt {s}=17.3$ GeV. The energy spectrum extends from about 3 TeV which corresponds to about 20 projectile spectators (indicating a “central” collision), to about 32 TeV which is close to the total beam energy and thus corresponds to extremely peripheral collisions. Note that the shape of this forward energy spectrum is the mirror image of the minimum bias transverse energy distribution of Fig. 7.3, both recorded by NA49. From both figures we see that the ideal head-on, b → 0 collision cannot be selected from these (or any other) data, owing to the facts that b = 0 carries zero geometrical weight, and that the diffuse Woods-Saxon nuclear density profiles lead to a fluctuation of participant nucleon number at given finite b. Thus the N _part fluctuation at finite weight impact parameters overshadows the genuinely small contribution of near zero impact parameters. Selecting “central” collisions, either by an on-line trigger cut on minimal forward energy or maximal total transverse energy or charged particle rapidity density, or by corresponding off-line selection, one thus faces a compromise between event statistics and selectivity for impact parameters near zero. In the example of Fig. 7.11 these considerations suggest a cut at about 8 TeV which selects the 5% most inelastic events, from among the overall minimum bias distribution, then to be labeled as “central” collisions. This selection corresponds to a soft cutoff at b ≤ 3 fm.

The selectivity of this, or of other less stringent cuts on collision centrality is then established by comparison to a Glauber or cascade model. The bottom panel of Fig. 7.11 employs the VENUS hadron/string cascade model [68] which starts from a Monte Carlo position sampling of the nucleons imbedded in Woods-Saxon nuclear density profiles but (unlike in a Glauber scheme with straight trajectory overlap projection) following the cascade of inelastic hadron/string multiplication, again by Monte Carlo sampling. It reproduces the forward energy data reasonably well and one can thus read off the average impact parameter and participant nucleon number corresponding to any desired cut on the percent fraction of the total minimum bias cross section. Moreover, it is clear that this procedure can also be based on the total minimum bias transverse energy distribution, Fig. 7.3, which is the mirror image of the forward energy distribution in Fig. 7.11, or on the total, and even the mid-rapidity charged particle density (Fig. 7.6). The latter method is employed by the RHIC experiments STAR and PHENIX.

How well this machinery works is illustrated in Fig. 7.12 by RHIC-PHOBOS results at $\sqrt {s}=200$ GeV [52]. The charged particle pseudo-rapidity density distributions are shown for central (3–6% highest N _ch cut) Cu+Cu collisions, with $\left <N_{\text{part}}\right >=100$, and semi-peripheral Au+Au collisions selecting the cut window (35–40%) such that the same $\left <N_{\text{part}}\right >$ emerges. The distributions are nearly identical. In extrapolation to N _part = 2 one would expect to find agreement between min. bias p+p, and “super-peripheral” A+A collisions, at least at high energy where the nuclear Fermi momentum plays no large role. Figure 7.13 shows that this expectation is correct [69]. As it is technically difficult to select N _part = 2 from A = 200 nuclei colliding, NA49 fragmented the incident SPS Pb beam to study ¹²C+¹²C and ²⁸Si+²⁸Si collisions [67]. These systems are isospin symmetric, and Fig. 7.13 thus plots $0.5 \; (\left <\pi ^+\right >+\left <\pi ^-\right >)/\left <N_{\mathrm {W}}\right >$ including p+p where N _W = 2 by definition. We see that the pion multiplicity of A+A collisions interpolates to the p+p data point.

Fig. 7.12

Charged hadron pseudo-rapidity distributions in Cu+Cu and Au+Au collisions at $\sqrt {s}=200$ GeV, with similar N _part ≈ 100 [52]

Fig. 7.13

Charged pion multiplicity normalized by N _W vs. centrality in p+p, C+C, Si+Si and Pb+Pb collisions at $\sqrt {s}=17.3$ GeV [67, 69]

Note that NA49 employs the term “wounded nucleon” number (N _W) to count the nucleons that underwent at least one inelastic nucleon-nucleon collision. This is what the RHIC experiments (that follow a Glauber model) call N _part whereas NA49 reserves this term for nucleons that underwent any inelastic collision. Thus N _W in Fig. 7.13 has the same definition as N _part in Figs. 7.4, 7.6, 7.8, and 7.12. We see that a smooth increase joins the p+p data, via the light A+A central collisions, to a saturation setting in with semi-peripheral Pb+Pb collisions, the overall, relative increase amounting to about 40% (as we saw in Fig. 7.4).

There is nothing like an $N_{\text{part}}^{1/3}$ increase (the thickness of the reactants) observed here, pointing to the saturation mechanism(s) mentioned in the previous section, which are seen from Fig. 7.13 to dampen the initial, fast increase once the primordial interaction volume contains about 80 nucleons. In the Glauber model view of successive collisions (to which we attach only symbolical significance at high $\sqrt {s}$) this volume corresponds to $\left <\nu \right > \approx 3$, and within the terminology of such models we might thus argue, intuitively, that the initial geometrical cross section, attached to the nucleon structure function as a whole, has disappeared at $\left <\nu \right > \approx 3$, all constituent partons being freed.

7.2.4 Gluon Saturation in A+A Collisions

We will now take a closer look at the saturation phenomena of high energy QCD scattering, and apply results obtained for deep inelastic electron-proton reactions to nuclear collisions, a procedure that relies on a universality of high energy hadron scattering. This arises at high $\sqrt {s}$, and at relatively low momentum transfer squared Q ² (the condition governing bulk charged particle production near mid-rapidity at RHIC, where Feynman x ≈ 0.01 and Q ² ≤ 5 GeV²). Universality comes about as the transverse resolution becomes higher and higher, with Q ², so that within the small area tested by the collision there is no difference whether the partons sampled there belong to the transverse gluon and quark density projection of any hadron species, or even of a nucleus. And saturation arises once the areal transverse parton density exceeds the resolution, leading to interfering QCD sub-amplitudes that do not reflect in the total cross section in a manner similar to the mere summation of separate, resolved color charges [61,62,63,64,65, 70, 71].

The ideas of saturation and universality are motivated by HERA deep inelastic scattering (DIS) data [72] on the gluon distribution function shown in Fig. 7.14 (left side). The gluon rapidity density, xG(x, Q ²) = (dN ^gluon)∕(dy) rises rapidly as a function of decreasing fractional momentum, x, or increasing resolution, Q ². The origin of this rise in the gluon density is, ultimately, the non-abelian nature of QCD. Due to the intrinsic non-linearity of QCD [70, 71], gluon showers generate more gluon showers, producing an avalanche toward small x. As a consequence of this exponential growth the spatial density of gluons (per unit transverse area per unit rapidity) of any hadron or nucleus must increase as x decreases [65]. This follows because the transverse size, as seen via the total cross section, rises more slowly toward higher energy than the number of gluons. This is illustrated in Fig. 7.14 (right side). In a head-on view of a hadronic projectile more and more partons (mostly gluons) appear as x decreases. This picture reflects a representation of the hadron in the “infinite momentum frame” where it has a large light-cone longitudinal momentum P ⁺ ≫ M. In this frame one can describe the hadron wave function as a collection of constituents carrying a fraction p ⁺ = xP ⁺, 0 ≤ x < 1, of the total longitudinal momentum [73] (“light cone quantization” method [74]). In DIS at large sqrts and Q ² one measures the quark distributions dN _q∕dx at small x, deriving from this the gluon distributions xG(x, Q ²) of Fig. 7.14.

Fig. 7.14

(Left) HERA data for the gluon distribution function as a function of fractional momentum x and square momentum transfer Q ² [72]. (Right) Saturation of gluons in a hadron; a head on view as x decreases [75]

It is useful [75] to consider the rapidity distribution implied by the parton distributions, in this picture. Defining $y=y_{\text{hadron}} - \ln (1/x)$ as the rapidity of the potentially struck parton, the invariant rapidity distribution results as

$$\displaystyle \begin{aligned} {\mathrm{d}} N/{\mathrm{d}} y = x \:{\mathrm{d}} N/{\mathrm{d}} x = xG(x,Q^2). {} \end{aligned} $$

(7.8)

At high Q ² the measured quark and gluon structure functions are thus simply related to the number of partons per unit rapidity, resolved in the hadronic wave function.

The above textbook level [74, 75] recapitulation leads, however, to an important application: the dN∕dy distribution of constituent partons of a hadron (or nucleus), determined by the DIS experiments, is similar to the rapidity distribution of produced particles in hadron-hadron or A+A collisions as we expect the initial gluon rapidity density to be represented in the finally observed, produced hadrons, at high $\sqrt {s}$. Due to the longitudinal boost invariance of the rapidity distribution, we can apply the above conclusions to hadron-hadron or A+A collisions at high $\sqrt {s}$, by replacing the infinite momentum frame hadron rapidity by the center of mass frame projectile rapidity, y _proj, while retaining the result that the rapidity density of potentially interacting partons grows with increasing distance from y _proj like

$$\displaystyle \begin{aligned} \Delta y \equiv y_{\text{proj}} - y = \ln(1/x). {} \end{aligned} $$

(7.9)

At RHIC energy, $\sqrt {s}= 200$ GeV, Δy at mid-rapidity thus corresponds to x < 10⁻² (well into the domain of growing structure function gluon density, Fig. 7.14), and the two intersecting partonic transverse density distributions thus attempt to resolve each other given the densely packed situation that is depicted in the lower circle of Fig. 7.14 (right panel). At given Q ² (which is modest, Q ² ≤ 5 GeV², for bulk hadron production at mid-rapidity) the packing density at mid-rapidity will increase toward higher $\sqrt {s}$ as

$$\displaystyle \begin{aligned} \Delta y^{\text{midrap}} \approx \ln(\sqrt{s}/M), \:\: \mbox{i.e.} \:\: 1/x \approx \sqrt{s}/M {} \end{aligned} $$

(7.10)

thus sampling smaller x domains in Fig. 7.14 according to Eq. (7.9). It will further increase in proceeding from hadronic to nuclear reaction partners A+A. Will it be in proportion to A ^4∕3? We know from the previous sections (Sects. 7.2.2 and 7.2.3) that this is not the case, the data indicating an increase with A ^1.08. This observation is, in fact caused by the parton saturation effect, to which we turn now.

For given transverse resolution Q ² and increasing 1∕x the parton density of Fig. 7.14 becomes so large that one cannot neglect their mutual interactions any longer. One expects such interactions to produce “shadowing”, a decrease of the scattering cross section relative to incoherent independent scattering [70, 71]. As an effect of such shadowed interactions there occurs [75] a saturation [61,62,63,64,65, 70, 71, 75] of the cross section at each given Q ², slowing the increase with 1∕x to become logarithmic once 1∕x exceeds a certain critical value x _s(Q ²). Conversely, for fixed x, saturation occurs for transverse momenta below some critical Q ²(x),

$$\displaystyle \begin{aligned} Q_{\mathrm{s}}^2(x) = \alpha_{\mathrm{s}} N_{\mathrm{c}} \: \frac{1}{\pi R^2} \: \frac{{\mathrm{d}} N}{{\mathrm{d}} y} {} \end{aligned} $$

(7.11)

where dN∕dy is the x-dependent gluon density (at $y=y_{\text{proj}} - \ln (1/x))$. $Q^2_{\mathrm {s}}$ is called the saturation scale. In Eq. (7.11) πR ² is the hadron area (in transverse projection), and α _sN _c is the color charge squared of a single gluon. More intuitively, $Q^2_{\mathrm {s}} (x)$ defines an inversely proportional resolution area F _s(x) and at each x we have to choose F _s(x) such that the ratio of total area πR ² to F _s(x) (the number of resolved areal pixels) equals the number of single gluon charge sources featured by the total hadron area. As a consequence the saturation scale $Q^2_{\mathrm {s}}(x)$ defines a critical areal resolution, with two different types of QCD scattering theory defined, at each x, for $Q^2 > Q^2_{\mathrm {s}}$ and $Q^2 < Q^2_{\mathrm {s}}$, respectively [62, 65, 75].

As one expects a soft transition between such theories, to occur along the transition line implied by $Q^2_{\mathrm {s}}(x)$, the two types of QCD scattering are best studied with processes featuring typical Q ² well above, or below $Q^2_{\mathrm {s}}(x)$. Jet production at $\sqrt {s} \ge 200$ GeV in $p\overline {p}$ or AA collisions with typical Q ² above about 10³ GeV², clearly falls into the former class, to be described e.g. by QCD DGLAP evolution of partonic showers [76]. The acronym DGLAP refers to the inventors of the perturbative QCD evolution of parton scattering with the “running” strong coupling constant α _s(Q ²), Dokshitzer, Gribov, Levine, Altarelli and Parisi. On the other hand, mid-rapidity bulk hadron production at the upcoming CERN LHC facility ($\sqrt {s}=14$ TeV for pp, and 5.5 TeV for A+A), with typical Q ² ≤ 5 GeV² at x ≤ 10⁻³, will present a clear case for QCD saturation physics, as formulated e.g. in the “Color Glass Condensate (CGC)” formalism developed by McLerran, Venugopalan and collaborators [64, 65, 75, 77]. This model develops a classical gluon field theory for the limiting case of a high areal occupation number density, i.e. for the conceivable limit of the situation depicted in Fig. 7.14 (right hand panel) where the amalgamating small x gluons would overlap completely, within any finite resolution area at modest Q ². Classical field theory captures, by construction, the effects of color charge coherence, absent in DGLAP parton cascade evolution theories [75]. This model appears to work well already at $\sqrt {s}$ as “low” as at RHIC, as far as small Q ² bulk charged particle production is concerned. We have illustrated this by the CGC model fits [64] to the PHOBOS charged particle rapidity distributions, shown in Fig. 7.7.

Conversely, QCD processes falling in the transition region between such limiting conditions, such that typical $Q^2 \approx Q^2_{\mathrm {s}}(x)$, should present observables that are functions of the ratio between the transferred momentum Q ² and the appropriate saturation scale, expressed by $Q^2_{\mathrm {s}}(x)$. As Q ² defines the effective transverse sampling area, and $Q^2_{\mathrm {s}}(x)$ the characteristic areal size at which saturation is expected to set in, a characteristic behavior of cross sections, namely that they are universal functions of $Q^2/Q^2_{\mathrm {s}}$, is called “geometric scaling”. The HERA ep scattering data obey this scaling law closely [78], and the idea arises to apply the universality principle that we mentioned above: at small enough x, all hadrons or nuclei are similar, their specific properties only coming in via the appropriate saturation scales $Q^2_{\mathrm {s}}(x,h)$ or $Q^2_{\mathrm {s}}(x,A)$. Knowing the latter for RHIC conditions we will understand the systematics of charged particle production illustrated in the previous chapter, and thus also be able to extrapolate toward LHC conditions in pp and AA collisions.

All data for the virtual photo-absorption cross section σ ^γp(x, Q ²) in deep inelastic ep scattering with x ≤ 0.01 (which is also the RHIC mid-rapidity x-domain) have been found [78] to lie on a single curve when plotted against $Q^2/Q^2_{\mathrm {s}}$, with

$$\displaystyle \begin{aligned} Q_{\mathrm{s}}^2(x) \sim \left( \frac{x_0}{x} \right)^\lambda \: 1 \; \mbox{GeV}^2 {}\end{aligned} $$

(7.12)

with λ ≃ 0.3 and x ₀ ≃ 10⁻⁴. This scaling [79] with $\tau =Q^2/Q^2_{\mathrm {s}}$ is shown in Fig. 7.15 (top panel) to interpolate all data. A chain of arguments, proposed by Armesto et al. [63] connects a fit to these data with photo-absorption data for (virtual) photon-A interactions [80] via the geometrical scaling ansatz

$$\displaystyle \begin{aligned} \frac{\sigma^{\gamma A} (\tau_{\mathrm{A}})}{\pi R^2_{\mathrm{A}}} = \frac{\sigma^{\gamma p} (\tau_{\mathrm{p}}=\tau_{\mathrm{A}})}{\pi R^2_{\mathrm{p}}} {}\end{aligned} $$

(7.13)

assuming that the scale in the nucleus grows with the ratio of the transverse parton densities, raised to the power 1∕δ (a free parameter),

$$\displaystyle \begin{aligned} Q^2_{\mathrm{s,A}}=Q^2_{\mathrm{s,p}}\left(\frac{A \pi R^2_{\mathrm{p}}}{\pi R^2_{\mathrm{A}}}\right)^{1/\delta}, \: \: \tau_{\mathrm{A}} = \tau_{\mathrm{h}} \left(\frac{\pi R^2_{\mathrm{A}}}{A \pi R^2_{\mathrm{h}}}\right)^{1/\delta}. {}\end{aligned} $$

(7.14)

Fig. 7.15

(Top) Geometric scaling of the virtual photo-absorption cross section σ ^γp on protons; (middle) cross sections for nuclei normalized according to Eq. (7.13); (bottom) the ratio of σ ^γA to a fit of σ ^γp (see [63] for data reference)

Figure 7.15 (middle and bottom panels) shows their fit to the nuclear photo-absorption data which fixes δ = 0.79 and $\pi R^2_{\mathrm {p}}=1.57$ fm² (see ref. [63] for detail). The essential step in transforming these findings to the case of A+A collisions is then taken by the empirical ansatz

$$\displaystyle \begin{aligned} \frac{{\mathrm{d}} N^{\text{AA}}}{{\mathrm{d}} y} \: (\mbox{at} \: y \simeq 0) \: \propto \: Q^2_{\mathrm{s,A}}(x) {} \pi R^2_{\mathrm{A}} \end{aligned} $$

(7.15)

by which the mid-rapidity parton (gluon) density dN∕dy in Eq. (7.11) gets related to the charged particle mid-rapidity density at y ≈ 0 [70, 81], measured in nucleus-nucleus collisions. Replacing, further, the total nucleon number 2A in a collision of identical nuclei of mass A by the number N _part of participating nucleons, the final result is [63]

$$\displaystyle \begin{aligned} \frac{1}{N_{\text{part}}} \: \: \frac{{\mathrm{d}} N^{\text{AA}}}{{\mathrm{d}} y} \: (\mbox{at} \: y \approx 0) = N_0 (\sqrt{s})^{\lambda} \: N^{\alpha}_{\text{part}} {} \end{aligned} $$

(7.16)

where the exponent α ≡ (1 − δ)∕3 δ = 0.089, and N ₀ = 0.47. The exponent α is far smaller than 1/3, a value that represents the thickness of the reactants, and would be our naive guess in a picture of “successive” independent nucleon participant collisions, whose average number $\left <\nu \right > \: \propto \: (N_{\text{part}}/2)^{1/3}$. The observational fact (see Fig. 7.13) that α < 1∕3 for mid-rapidity low Q ² bulk hadron production in A+A collisions illustrates the importance of the QCD saturation effect. This is shown [63] in Fig. 7.16 where Eq. (7.16) is applied to the RHIC PHOBOS data for mid-rapidity charged particle rapidity density per participant pair, in Au+Au collisions at $\sqrt {s}=19.6$, 130 and 200 GeV [82], also including a prediction for LHC energy. Note that the factorization of energy and centrality dependence, implied by the RHIC data [52], is well captured by Eq. (7.11) and the resulting fits in Fig. 7.16. Furthermore, the steeper slope, predicted for N _part ≤ 60 (not covered by the employed data set), interpolates to the corresponding pp and $p\overline {p}$ data, at N _part = 2. It resembles the pattern observed in the NA49 data (Fig. 7.13) for small N _part collisions of light A+A systems, at $\sqrt {s}=17$–20 GeV, and may be seen, to reflect the onset of QCD saturation. Finally we note that the conclusions of the above, partially heuristic approach [63], represented by Eqs. (7.13)–(7.16), have been backed up by the CGC theory of McLerran and Venugopulan [64, 65, 75], predictions of which we have illustrated in Fig. 7.7.

Fig. 7.16

Saturation model fit [63] applied to RHIC charged hadron multiplicity data at mid-rapidity normalized by number of participant pairs, at various energies [82]. Also shown is an extrapolation to $p \overline {p}$ data and a prediction for minimum bias Pb+Pb collisions at LHC energy, $\sqrt {s}=5500$ GeV

Bulk hadron production in AA collisions at high $\sqrt {s}$ can be related, via the assumption of universality of high energy QCD scattering, to the phenomenon of geometric scaling first observed in HERA deep inelastic ep cross sections. The underlying feature is a QCD saturation effect arising from the diverging areal parton density, as confronted with the limited areal resolution Q ², inherent in the considered scattering process. The “saturation scale” $Q^2_{\mathrm {s}}(x,A)$ captures the condition that a single partonic charge source within the transverse partonic density profile can just be resolved by a sufficiently high Q ². Bulk hadron production in A+A collisions falls below this scale.

7.2.5 Transverse Phase Space: Equilibrium and the QGP State

At RHIC energy, $\sqrt {s}=200$ GeV, the Au+Au collision reactants are longitudinally contracted discs. At a nuclear radius R ≈ A ^1∕3 fm and Lorentz γ ≈ 100 their primordial interpenetration phase ends at time τ ₀ ≤ 0.15 fm/c. This time scale is absent in e ⁺e ⁻ annihilation at similar $\sqrt {s}$ where τ ₀ ≈ 0.1 fm/c marks the end of the primordial pQCD partonic shower evolution [83] during which the initially created $q \overline {q}$ pair, of “virtually” $Q=\sqrt {s}/2$ each, multiplies in the course of the QCD DGLAP evolution in perturbative vacuum, giving rise to daughter partons of far lower virtuality, of a few GeV. In A+A collisions this shower era should last longer, due to the interpenetrational spread of primordial collision time. It should be over by about 0.25 fm/c. The shower partons in e ⁺e ⁻ annihilation are localized within back to back cone geometry reflecting the directions of the primordial quark pair. The eventually observed “jet” signal, created by an initial Q ² of 10⁴ GeV², is established by then. Upon a slow-down of the dynamical evolution time scale to τ ≈ 1 fm/c the shower partons fragment further, acquiring transverse momentum and yet lower virtuality, then to enter a non perturbative QCD phase of color neutralization during which hadron-like singlet parton clusters are formed. Their net initial pQCD virtuality, in pQCD vacuum, is recast in terms of non-perturbative vacuum hadron mass. The evolution ends with on-shell, observed jet-hadrons after about 3 fm/c of overall reaction time.

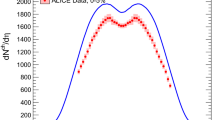
Remarkably, even in this, somehow most elementary process of QCD evolution, an aspect of equilibrium formation is observed, not in the narrowly focused final dijet momentum topology but in the relative production rates of the various created hadronic species. This so-called “hadrochemical” equilibrium among the hadronic species is documented in Fig. 7.17. The hadron multiplicities per e ⁺e ⁻ annihilation event at $\sqrt {s}=91.2$ GeV [38] are confronted with a Hagedorn [38] canonical statistical Gibbs ensemble prediction [84] which reveals that the apparent species equilibrium was fixed at a temperature of T = 165 MeV, which turns out to be the universal hadronization temperature of all elementary and nuclear collisions at high $\sqrt {s}$ (Hagedorns limiting temperature of the hadronic phase of matter). We shall return to this topic in Sect. 7.3 but note, for now, that reactions with as few as 20 charged particles exhibit such statistical equilibrium properties, a pre-requisite for application of thermodynamic or hydrodynamic concepts.

Fig. 7.17

Hadron multiplicities in LEP e ⁺e ⁻ annihilation at $\sqrt {s}=91.2$ GeV confronted with the predictions of the canonical statistical hadronization model [84]

What happens with parton (and hadron) dynamics in A+A collisions after τ ₀? There will not be a QCD evolution in vacuum (which would be over after 3 fm/c) as the transverse radius of the interacting system is large. It may grow to about twice the nuclear radius, i.e. to about 15 fm before interactions cease; i.e. the system needs about 15 fm/c to decouple. This simple fact is the key to our expectation that the expansive evolution of the initial high energy density deposited in a cylinder of considerable diameter (about 10 fm), may create certain equilibrium properties that allow us to treat the contained particles and energy in terms of thermodynamic phases of matter, such as a partonic QGP liquid, or a hadronic liquid or gas, etc. Such that the expansion dynamics makes contact to the phase diagram illustrated in Fig. 7.1. This expectation turns out to be justified as we shall describe in Sects. 7.3 and 7.4. What results for the evolution after τ ₀ in a central A+A collision is sketched in Fig. 7.18

Fig. 7.18

Schematic light cone diagram of the evolution of a high energy heavy ion collision, indicating a formation phase τ ₀ (see text)

by means of a schematic 2-dimensional light cone diagram, which is entered by the two reactant nuclei along z = t trajectories where z is the beam direction and Lorentz contraction has been taken to an extreme, such that there occurs an idealized t = z = 0 interaction “point”. Toward positive t the light cone proper time profiles of progressing parton-hadron matter evolution are illustrated. The first profile illustrated here corresponds to the end of formation time τ ₀. From our above discussion of the e ⁺e ⁻ annihilation process one obtains a first estimate, τ ₀ ≥ 0.25 fm/c (including interpenetration time of 0.15 fm/c at RHIC) which refers to processes of very high Q ² ≥ 10³ GeV², far above the saturation scale $Q^2_{\mathrm {s}}$ discussed in the previous section. The latter scale has to be taken into account for low p _T hadron production.

It is the specific resolution scale Q ² of a QCD sub-process, as enveloped in the overall collision dynamics of two slabs of given transverse partonic structure function density, that determines which fraction of the constituent partons enters interaction. In the simple case of extremely high Q ² processes the answer is that all constituents are resolved. However, at modest Q ² (dominating bulk hadron production) the characteristic QCD saturation scale $Q^2_{\mathrm {s}} (x)$ gains prominence, defined such that processes with $Q^2 < Q^2_{\mathrm {s}}$ do not exploit the initial transverse parton densities at the level of independent single constituent color field sources (see Eq. (7.11)). For such processes the proper formation time scale, τ ₀, is of order of the inverse saturation momentum [61], 1∕Q _s ∼ 0.2 fm/c at $\sqrt {s}=200$ GeV. The first profile of the time evolution, sketched in Fig. 7.18, should correspond to proper time t = τ ₀ = 0.25 fm/c at RHIC energy. At top SPS energy, $\sqrt {s}=17.3$ GeV, we cannot refer to such detailed QCD considerations. A pragmatic approach suggests to take the interpenetration time, at γ ≈ 8.5, for guidance concerning the formation time, which thus results as τ ₀ ≈ 1.5 fm/c.

In summary of the above considerations we assume that the initial partonic color sources, as contained in the structure functions (Fig. 7.14), are spread out in longitudinal phase space after light cone proper time t = τ ₀ ≈ 0.2 fm/c, at top RHIC energy, and after τ ₀ ≈ 1.5 fm/c at top SPS energy. No significant transverse expansion has occurred at this early stage, in a central collision of A ≈ 200 nuclei with transverse diameter of about 12 fm. The Bjorken estimate [45] of initial energy density 𝜖 (Eq. (7.1)) refers to exactly this condition, after formation time τ ₀. In order to account for the finite longitudinal source size and interpenetration time, at RHIC, we finally put the average τ ₀ ≈ 0.3 fm, at $\sqrt {s}=200$ GeV, indicating the “initialization time” after which all partons that have been resolved from the structure functions are engaged in shower multiplication. As is apparent from Fig. 7.18, this time scale is Lorentz dilated for partons with a large longitudinal momentum, or rapidity. This means that the slow particles are produced first toward the center of the collision region, and the fast (large rapidity) particles are produced later, away from the collision region. This Bjorken “inside-out” correlation [45] between coordinate- and momentum-space is similar to the Hubble expansion pattern in cosmology: more distant galaxies have higher outward velocities. This means that the matter created in A+A collisions at high $\sqrt {s}$ is also born expanding, however with the difference that the Hubble flow is initially one dimensional along the collision axis. This pattern will continue, at $\sqrt {s}=200$ GeV, until the system begins to feel the effects of finite size in the transverse direction which will occur at some time t ₀ in the vicinity of 1 fm/c. However, the tight correlation between position and momentum initially imprinted on the system will survive all further expansive evolution of the initial “firetube”, and is well recovered in the expansion pattern of the finally released hadrons of modest p _T as we shall show when discussing radial flow and pion pair Bose-Einstein momentum correlation (see Sects. 7.2.6 and 7.7).

In order to proceed to a more quantitative description of the primordial dynamics (that occurs onward from τ ₀ for as long the time period of predominantly longitudinal expansion might extend) we return to the Bjorken estimate of energy density, corresponding to this picture [45], as implied by Eq. (7.1), which we now recast as

$$\displaystyle \begin{aligned} \epsilon = \left(\frac{{\mathrm{d}} N_{\mathrm{h}}}{{\mathrm{d}} y} \right) \left<E^T_{\mathrm{h}}\right>(\pi \: R^2_{\mathrm{A}} \: t_0)^{-1} {} \end{aligned} $$

(7.17)

where the first term is the (average) total hadron multiplicity per unit rapidity which, multiplied with the average hadron transverse energy, equals the total transverse energy recorded in the calorimetric study shown in Fig. 7.3, as employed in Eq. (7.1). The quantity R _A is, strictly speaking, not the radius parameter of the spherical Woods-Saxon nuclear density profile but the rms of the reactant overlap profiles as projected onto the transverse plane (and thus slightly smaller than R _A ≈ A ^1∕3 fm). Employing A ^1∕3 here (as is done throughout) leads to a conservative estimate of 𝜖, a minor concern. However, the basic assumption in Eq. (7.17) is to identify the primordial transverse energy “radiation”, of an interactional cylindric source of radius R _A and length t ₀ (where τ ₀ ≤ t ₀ ≤ 1 fm/c, not Lorentz dilated at midrapidity), with the finally emerging bulk hadronic transverse energy. We justify this assumption by the two observations, made above, that

• 1. the bulk hadron multiplicity density per unit rapidity (dN _h)∕(dy) resembles the parton density, primordially released at saturation scale τ ₀ (Figs. 7.7 and 7.16) at $\sqrt {s}=200$ GeV, and that

• 2. the global emission pattern of bulk hadrons (in rapidity and p _T) closely reflects the initial correlation between coordinate and momentum space, characteristic of a primordial period of a predominantly longitudinal expansion, as implied in the Bjorken model.

Both these observations are surprising, at first sight. The Bjorken model was conceived for elementary hadron collisions where the expansion proceeds into vacuum, i.e. directly toward observation. Figure 7.18 proposes that, to the contrary, primordially produced partons have to transform through further, successive stages of partonic and hadronic matter, at decreasing but still substantial energy density, in central A+A collisions. The very fact of high energy density, with implied short mean free path of the constituent particles, invites a hydrodynamic description of the expansive evolution. With initial conditions fixed between τ ₀ and t ₀, an ensuing 3-dimensional hydrodynamic expansion would preserve the primordial Bjorken-type correlation between position and momentum space, up to lower density conditions and, thus, close to emission of the eventually observed hadrons. We thus feel justified to employ Eq. (7.1) or (7.17) for the initial conditions at RHIC, obtaining [61, 84]

$$\displaystyle \begin{aligned} 6 \: \mbox{GeV/fm}^3 \le \epsilon \le 20 \: \mbox{GeV/fm}^3 {} \end{aligned} $$

(7.18)

for the interval 0.3 fm∕c ≤ t ₀ ≤ 1 fm/c, in central Au+Au collisions at y ≈ 0 and $\sqrt {s}=200$ GeV. The energy density at top SPS energy, $\sqrt {s}=17.3$ GeV, can similarly be estimated [43, 44] to amount to about 3 GeV/fm³ at a t ₀ of 1 fm/c but we cannot identify conditions at τ ₀ < t ₀ in this case as the mere interpenetration of two Pb nuclei takes 1.4 fm/c. Thus the commonly accepted t ₀ = 1 fm/c may lead to a high estimate. An application of the parton-hadron transport model of Ellis and Geiger [85, 86] to this collision finds 𝜖 = 3.3 GeV/fm³ at t = 1 fm/c. A primordial energy density of about 3 GeV/fm³ is 20 times ρ ₀ ≈ 0.15 GeV/fm³, the average energy density of ground state nuclear matter, and it also exceeds, by far, the critical QCD energy density, of 0.6 ≤ 𝜖 _c ≤ 1 GeV/fm³ according to lattice QCD [48]. The initial dynamics thus clearly proceeds in a deconfined QCD system also at top SPS energy, and similarly so with strikingly higher energy density, at RHIC, where time scales below 1 fm/c can be resolved.

However, in order now to clarify the key question as to whether, and when conditions of partonic dynamical equilibrium may arise under such initial conditions, we need estimates both of the proper relaxation time scale (which will, obviously, depend on energy density and related collision frequency), and of the expansion time scale as governed by the overall evolution of the collision volume. Only if τ (relax.) < τ (expans.) one may conclude that the “deconfined partonic system” can be identified with a “deconfined QGP state of QCD matter” as described e.g. by lattice QCD, and implied in the phase diagram of QCD matter suggested in Fig. 7.1.

For guidance concerning the overall time-order of the system evolution we consider information [87] obtained from Bose-Einstein correlation analysis of pion pair emission in momentum space (for detail see Sect. 7.7). Note that pions should be emitted at any stage of the evolution, after formation time, from the surface regions of the evolving “fire-tube”. Bulk emission of pions occurs, of course, after hadronization (the latest stages illustrated in the evolution sketch given in Fig. 7.18). The dynamical pion source expansion models by Heinz [88] and Sinyukov [89] elaborate a Gaussian emission time profile, with mean τ _f (the decoupling time) and width Δτ (the duration of emission).

Figure 7.19 shows an application of this analysis to central Pb+Pb collision negative pion pair correlation data obtained by NA49 at top SPS energy, $\sqrt {s}=17.3$ GeV [90], where τ _f ≈ 8 fm/c and Δτ ≈ 4 fm/c (note that τ = 0 in Fig. 7.19 corresponds, not to interaction time t = 0 but to t ≈ 1.4 fm/c, the end of the interpenetration phase). We see, first of all, that the overall dynamical evolution of a central Pb+Pb collision at $\sqrt {s}=17.3$ GeV is ending at about 15 fm/c; the proper time defines the position of the last, decoupling profile illustrated in Fig. 7.18, for the SPS collisions considered here. While the details of Fig. 7.19 will turn out to be relevant to our later discussion of hadronization (Sect. 7.3) and hadronic expansion (Sect. 7.4), we are concerned here with the average proper time at which the partonic phase ends. After consideration of the duration widths of these latter expansion phases [86, 87] one arrives at an estimate for the average time, spent before hadronization, of Δt = 3–4 fm/c, again in agreement with the parton cascade model mentioned above [86]. This model also leads to the conclusion that parton thermal equilibrium is, at least, closely approached locally in these central Pb+Pb collisions as far as mid-rapidity hadron production is concerned (at forward-backward rapidity the cascade re-scattering processes do not suffice, however).

Fig. 7.19

Time profile of pion decoupling rate from the fireball in a central Pb+Pb collision, with τ = 0 the end of the formation phase. Bose-Einstein correlation of π ⁻π ⁻pairs yields an average Gaussian decoupling profile with τ _f = 8 fm/c and duration of emission parameter Δτ = 4 fm/c [87, 88]

This finding agrees with earlier predictions of τ _relax = 1–2 fm/c at top SPS energy [91]. However we note that all such calculations employ perturbative QCD methods, implying the paradoxical consequence that equilibrium is closely approached only at the end of the partonic phase, at such low $\sqrt {s}$, i.e. in a QGP state at about T = 200 MeV which is, by definition, of non-perturbative nature. We shall return to the question of partonic equilibrium attainment at SPS energy in the discussion of the hadronization process in nuclear collisions (Sect. 7.3).

Equilibrium conditions should set in earlier at top RHIC energy. As transverse partonic expansion should set in after the proper time interval 0.3 fm∕c ≤ t ₀ ≤ 1 fm∕c (which is now resolved by the early dynamics, unlike at top SPS energy), we take guidance from the Bjorken estimate of primordial energy density which is based on transverse energy production data. Conservatively interpreting the result in Eq. (7.18) we conclude that 𝜖 is about four times higher than at $\sqrt {s}=17.3$ GeV in the above proper time interval. As the binary partonic collision frequency scales with the square of with the square of the density ρ (related to the energy density 𝜖 via the relation 𝜖 = $\left <E\right >\rho$ = Tρ), and is inversely proportional to the relaxation time τ _relax we expect

$$\displaystyle \begin{aligned} \tau_{\text{relax}}\propto (1/\rho)^2 \approx (T/\epsilon)^{2} {} \end{aligned} $$

(7.19)

which implies that τ _relax(RHIC) ≈ 0.25 τ _relax (SPS) ≈ 0.5 fm/c if we employ the estimate T(RHIC) = 2T(SPS). This crude estimate is, however, confirmed by the parton transport model of Molar and Gyulassy [92].

Partonic equilibration at $\sqrt {s}=200$ GeV should thus set in at a time scale commensurate to the (slightly smaller) formation time scale, at which the to be participant partons are resolved from the initial nucleon structure functions and enter shower multiplication. Extrapolating to the conditions expected at LHC energy ($\sqrt {s}=5.5$ TeV for A+A collisions), where the initial parton density of the structure functions in Fig. 7.14 is even higher (x ≈ 10⁻³ at mid-rapidity), and so is the initial energy density, we may expect conditions at which the resolved partons are almost “born into equilibrium”.

Early dynamical local equilibrium at RHIC is required to understand the observations concerning elliptic flow, with which we shall deal, in detail, in Sect. 7.4. This term refers to a collective anisotropic azimuthal emission pattern of bulk hadrons in semi-peripheral collisions, a hydrodynamical phenomenon that originates from the initial geometrical non-isotropy of the primordial interaction zone [93, 94]. A detailed hydrodynamic model analysis of the corresponding elliptic flow signal at RHIC [95] leads to the conclusion that local equilibrium (a prerequisite to the hydrodynamic description) sets in at t ₀ ≈ 0.6 fm/c. This conclusion agrees with the estimate via Eq. (7.19) above, based on Bjorken energy density and corresponding parton collisions frequency.

We note that the concept of a hydrodynamic evolution appears to be, almost necessarily ingrained in the physics of a system born into (Hubble-type) expansion, with a primordial correlation between coordinate and momentum space, and at extreme initial parton density at which the partonic mean free path length λ is close to the overall spatial resolution resulting from the saturation scale, i.e. λ ≈ 1∕Q _s.

The above considerations suggest that a quark-gluon plasma state should be created early in the expansion dynamics at $\sqrt {s}=200$ GeV, at about T = 300 MeV, that expands hydrodynamically until hadronization is reached, at T ≈ 165–170 MeV. Its manifestations will be considered in Sects. 7.3–7.6. At the lower SPS energy, up to 17.3 GeV, we can conclude, with some caution, that a deconfined hadronic matter system should exist at T ≈ 200 MeV, in the closer vicinity of the hadronization transition. It may closely resemble the QGP state of lattice QCD, near T _c.

7.2.6 Bulk Hadron Transverse Spectra and Radial Expansion Flow

In this chapter we analyze bulk hadron transverse momentum spectra obtained at SPS and RHIC energy, confronting the data with predictions of the hydrodynamical model of collective expansion matter flow that we have suggested in the previous section, to arise, almost necessarily, from the primordial Hubble-type coupling between coordinate and momentum space that prevails at the onset of the dynamical evolution in A+A collisions at high $\sqrt {s}$. As all hadronic transverse momentum spectra initially follow an approximately exponential fall-off (see below) the bulk hadronic output is represented by thermal transverse spectra at p _T ≤ 2 GeV/c. We shall turn to high p _T information in later sections.

Furthermore we shall focus here on mid-rapidity production in near central A+A collisions, because hydrodynamic models refer to an initialization period characterized by Bjorken-type longitudinal boost invariance, which we have seen in Figs. 7.7 and 7.9 to be restricted to a relatively narrow interval centered at mid-rapidity. Central collisions are selected to exploit the azimuthal symmetry of emission, in an ideal impact parameter b → 0 geometry. We thus select the predominant, relevant hydrodynamic “radial flow” expansion mode, from among other, azimuthally oriented (directed) flow patterns that arise once this cylindrical symmetry (with respect to the beam direction) is broken in finite impact parameter geometries.

In order to define, quantitatively, the flow phenomena mentioned above, we rewrite the invariant cross section for production of hadron species i in terms of transverse momentum, rapidity, impact parameter b and azimuthal emission angle φ _p (relative to the reaction plane),

$$\displaystyle \begin{aligned} \frac{{\mathrm{d}} N_i(b)}{p_{\mathrm{T}} \;{\mathrm{d}} p_{\mathrm{T}} \;{\mathrm{d}} y \;{\mathrm{d}} \varphi_{\mathrm{p}}} = \frac{1}{2 \: \pi}\: \frac{{\mathrm{d}} N_i(b)}{p_{\mathrm{T}} \;{\mathrm{d}} p_{\mathrm{T}} \;{\mathrm{d}} y} \: {\left[1 + 2v_1^i \: (p_{\mathrm{T}},b) \cos \varphi_{\mathrm{p}} + 2v_2^i \: (p_{\mathrm{T}},b) \cos (2 \varphi_{\mathrm{p}})+ \dots \right]} {} \end{aligned} $$

(7.20)

where we have expanded the dependence on φ _p into a Fourier series. Due to reflection symmetry with respect to the reaction plane in collisions of identical nuclei, only cosine terms appear. Restricting to mid-rapidity production all odd harmonics vanish, in particular the “directed flow” coefficient $v^i_1$, and we have dropped the y-dependence in the flow coefficients $v^i_1$ and $v^i_2$. The latter quantifies the amount of “elliptic flow”, to which we turn in Sect. 7.4. In the following, we will restrict to central collisions which we shall idealize as near-zero impact parameter processes governed by cylinder symmetry, whence all azimuthal dependence (expressed by the $v^i_1, \: v^i_2, \dots$ terms) vanishes, and the invariant cross section reduces to the first term in Eq. (7.20), which by definition also corresponds to all measurements in which the orientation of the reaction plane is not observed.

Typical transverse momentum spectra of the latter type are shown in Fig. 7.20, for charged hadron production in Au+Au collisions at $\sqrt {s}=200$ GeV, exhibiting mid-rapidity data at various collision centralities [97]. We observe a clear-cut transition, from bulk hadron emission at p _T ≤ 2 GeV/c featuring a near-exponential cross section (i.e. a thermal spectrum), to a high p _T power-law spectral pattern. Within the context of our previous discussion (Sect. 7.2.4) we tentatively identify the low p _T region with the QCD physics near saturation scale. Hadron production at p _T → 10 GeV/c should, on the other hand, be the consequence of primordial leading parton fragmentation originating from “hard”, high Q ² perturbative QCD processes.

Fig. 7.20

Transverse momentum spectra of charged hadrons in Au+Au collisions at $\sqrt {s}=200$ GeV, in dependence of collision centrality [97] (offset as indicated), featuring transition from exponential to power law shape

We thus identify bulk hadron production at low p _T as the emergence of the initial parton saturation conditions that give rise to high energy density and small equilibration time scale, leading to a hydrodynamical bulk matter expansion evolution. Conversely, the initially produced hard partons, from high Q ² processes, are not thermalized into the bulk but traverse it, as tracers, while being attenuated by medium-induced rescattering and gluon radiation, the combined effects being reflected in the high p _T inclusive hadron yield, and in jet correlations of hadron emission. We shall turn to the latter physics observables in Sect. 7.5, while staying here with low p _T physics, related to hydrodynamical expansion modes, focusing on radially symmetric expansion.

In order to infer from the spectral shapes of the hadronic species about the expansion mechanism, we first transform to the transverse mass variable, $m_{\mathrm {T}}=(p^2_{\mathrm {T}} + m^2)^{1/2}$, via

$$\displaystyle \begin{aligned} \frac{1}{2\pi} \: \frac{{\mathrm{d}} N_i}{p_{\mathrm{T}} \;{\mathrm{d}} p_{\mathrm{T}} \;{\mathrm{d}} y} = \frac{1}{2 \pi} \: \frac{{\mathrm{d}} N_i}{m_{\mathrm{T}} \;{\mathrm{d}} m_{\mathrm{T}} \;{\mathrm{d}} y} {} \end{aligned} $$

(7.21)

because it has been shown in p+p collisions [98] near RHIC energy that the m _T distributions of various hadronic species exhibit a universal pattern (“m _T scaling”) at low m _T:

$$\displaystyle \begin{aligned} \frac{1}{2\pi} \: \frac{{\mathrm{d}} N_i}{m_{\mathrm{T}} \;{\mathrm{d}}m_{\mathrm{T}} \;{\mathrm{d}} y} = A_i \: \exp (-m^i_{\mathrm{T}} / T) {} \end{aligned} $$

(7.22)

with a universal inverse slope parameter T and a species dependent normalization factor A. Hagedorn showed [99] that this scaling is characteristic of an adiabatic expansion of a fireball at temperature T. We recall that, on the other hand, an ideal hydrodynamical expansion is isentropic.

Figure 7.21 shows the $\sqrt {s}$ dependence of the average transverse kinetic energy $\left <m^i_{\mathrm {T}}\right >-m^i$ for pions, kaons and protons observed at mid-rapidity in central Au+Au/Pb+Pb collisions [54]. Similarly, the inverse slope parameter T resulting from a fit of Eq. (7.22) to K ⁺ and K ⁻ transverse mass spectra (at p _T ≤ 2 GeV/c) is shown in Fig. 7.22, both for nuclear and p+p collisions [100]. We see, first of all, that m _T scaling does not apply in A+A collisions, and that the kaon inverse slope parameter, T ≈ 230 MeV over the SPS energy regime, cannot be identified with the fireball temperature at hadron formation which is T _h ≈ 165 MeV from Fig. 7.1. The latter is seen, however, to be well represented by the p+p spectral data exhibited in the left panel of Fig. 7.22. There is, thus, not only thermal energy present in A+A transverse expansion, but also hydrodynamical radial flow.

Fig. 7.21

The average transverse kinetic energy $\left <m_{\mathrm {T}} \right >- m_0$ for pions, kaons and protons vs. $\sqrt {s}$ in central Au+Au/Pb+Pb collisions [54]. Open symbols represent negative hadrons

Fig. 7.22

The inverse slope parameter T of Eq. (7.22) for K ⁺and K ⁻ transverse mass spectra at p _T < 2 GeV/c and mid-rapidity in central A+A, and in minimum bias p+p collisions [100]

We note that the indications in Figs. 7.21 and 7.22, of a plateau in both $\left <m_{\mathrm {T}}\right >$ and T, extending over the domain of SPS energies, $6 \le \sqrt {s} \le 17$ GeV, have not yet been explained by any fundamental expansive evolution model, including hydrodynamics. Within the framework of the latter model, this is a consequence of the initialization problem [96] which requires a detailed modeling, both of primordial energy density vs. equilibration time scale, and of the appropriate partonic matter equation of state (EOS) which relates expansion pressure to energy density. At top RHIC energy, this initialization of hydro-flow occurs, both, at a time scale t ₀ ≈ 0.6 fm/c which is far smaller than the time scale of eventual bulk hadronization (t ≈ 3 fm/c), and at a primordial energy density far in excess of the critical QCD confinement density. After initialization, the partonic plasma phase thus dominates the overall expansive evolution, over a time interval far exceeding the formation and relaxation time scale.

Thus, at RHIC energy, parton transport [92] and relativistic hydrodynamic [95, 96] models establish a well developed expansion mode that survives the subsequent stages of hadronization and hadronic expansion. This is reflected in their success in describing elliptic flow. On the other hand, the hydrodynamical model far overestimates elliptic flow at SPS energy [96] at which, as we have shown in Sect. 7.2.5, the initialization period may be not well separated from the confinement (hadronization) stage. Thus, whereas the expansion evolution at $\sqrt {s}=200$ GeV (occurring at near-zero baryo-chemical potential in Fig. 7.1) “races” across the parton-hadron phase boundary with fully established flow patterns, near μ _B = 0 where lattice QCD predicts the phase transformation to be merely a soft cross-over [16], the dynamics at $\sqrt {s}=10$–20 GeV may originate from only slightly above, or even at the phase boundary, thus sampling the domain 200 ≤ μ _B ≤ 500 MeV where the equation of state might exhibit a “softest point” [96]. The hydrodynamic model thus faces formidable uncertainties regarding initialization at SPS energy.

The plateau in Figs. 7.21 and 7.22 may be the consequence of the fact that not much flow is generated in, or transmitted from the partonic phase, at SPS energies, because it is initialized close to the phase boundary [100] where the expected critical point [9, 10] (Fig. 7.1), and the corresponding adjacent first order phase transition might focus [101] or stall [96] the expansion trajectory, such that the observed radial flow stems almost exclusively from the hadronic expansion phase. The SPS plateau, which we shall subsequently encounter in other bulk hadron variables (elliptic flow, HBT radii) might thus emerge as a consequence of the critical point or, in general, of the flatness of the parton-hadron coexistence line. RHIC dynamics, on the other hand, originates from far above this line.

Hadronic expansion is known to proceed isentropically [102]: commensurate to expansive volume increase the momentum space volume must decrease, from a random isotropic thermal distribution to a restricted momentum orientation preferentially perpendicular to the fireball surface, i.e. radial. The initial thermal energy, implied by the hadron formation temperature T _H = 165 MeV, will thus fall down to a residual T _F at hadronic decoupling from the flow field (“thermal freeze-out”) plus a radial transverse kinetic energy term $m_i \left < \beta _{\mathrm {T}}\right >^2$ where m _i is the mass of the considered hadron species and $\left <\beta _{\mathrm {T}}\right >$ the average radial velocity. We thus expect [103] for the slope of equation (7.22):

$$\displaystyle \begin{aligned} T=T_{\mathrm{F}}+m_i\left<\beta _{\mathrm{T}}\right>^2, \: p_{\mathrm{T}} \le 2 \: \mbox{GeV}/c {} \end{aligned} $$

(7.23)

and

$$\displaystyle \begin{aligned} T=T_{\mathrm{F}} \left( \frac{1+\left<v_{\mathrm{T}}\right>}{1-\left<v_{\mathrm{T}}\right>} \right)^{1/2}, \: p_{\mathrm{T}} \gg m_i {} \end{aligned} $$

(7.24)

the latter expression valid at p _T larger than hadron mass scale (T then is the “blue-shifted temperature” at decoupling [104] and $\left <v_{\mathrm {T}}\right >$ the average transverse velocity). The assumption that radial flow mostly originates from the hadronic expansion phase is underlined by the proportionality of flow energy to hadron mass (Eq. (7.23)).

Figure 7.23 illustrates this proportionality, by a recent compilation [103] of RHIC results for central Au+Au collisions at $\sqrt {s}= 200$ GeV, and SPS results for central Pb+Pb collisions at top SPS energy, $\sqrt {s}=17.3$ GeV. At the latter energy the slope parameter of the Φ meson is seen to be close to that of the similar mass baryons p and Λ, emphasizing the occurrence of m _i scaling as opposed to valence quark number scaling that we will encounter in RHIC elliptic flow data [94]. As is obvious from Fig. 7.23 the multi-strange hyperons and charmonia exhibit a slope saturation which is usually explained [103] as a consequence of their small total cross sections of rescattering from other hadrons, leading to an early decoupling from the bulk hadron radial flow field, such that $\left <\beta _{\mathrm {T}}\right > _{\Omega } \: < \: \left <\beta _{\mathrm {T}}\right >_{\mathrm {p}}$.

Fig. 7.23

Hadron slope parameters T at mid-rapidity as a function of mass. For Pb+Pb at $\sqrt {s}=17.3$ GeV (triangles) and Au+Au at $\sqrt {s}=200$ GeV (circles); from [103]

According to our observations with Eq. (7.23) a hydrodynamical ansatz for the transverse mass spectrum of hadrons should thus contain the variables “true temperature” T _F at decoupling from the flow field, and its average velocity $\left <\beta _{\mathrm {T}}\right >$, common to all hadrons. This is the case for the blast wave model [104] developed as an approximation to the full hydrodynamic formalism [96], assuming a common decoupling or “freeze-out” from flow, for all hadronic species, and a boost-invariant longitudinal expansion:

$$\displaystyle \begin{aligned} \frac{{\mathrm{d}} N_i}{m_{\mathrm{T}} \;{\mathrm{d}} m_{\mathrm{T}} \;{\mathrm{d}} y} = A_i \: m_{\mathrm{T}} \: K_1 \: \left(\frac{m_{\mathrm{T}} \;\text{cosh} \, \rho}{T_{\mathrm{F}}} \right) \: I_0 \left( \frac{p_{\mathrm{T}} \;\text{sinh} \, \rho}{T_{\mathrm{F}}} \right) {} \end{aligned} $$

(7.25)

where ρ = tanh⁻¹β _T. In an extended version of this model a function is included that describes the radial profile of the transverse velocity field, $\beta _{\mathrm {T}}(r)=\beta _{\mathrm {T}}^{\max } \: r/R$, instead of employing a fixed β _T at decoupling [106]. Figure 7.24 flow shows [54] the resulting energy dependence of T _F and $\left <\beta _{\mathrm {T}}\right >$, for the same set of data as implied already in Figs. 7.21 and 7.22. The “true” decoupling temperature rises steeply at the AGS and less so at SPS energy (as does $\left <\beta _{\mathrm {T}}\right >$), to a value of about 95 MeV at top SPS energy, which is considerably lower than the chemical freeze-out temperature, T _H = 165 MeV, at which the hadronic species relative yield composition of the hadronic phase becomes stationary (see Sect. 7.3, and Fig. 7.1). Chemical decoupling thus occurs early, near the parton-hadron phase boundary, whereas hadronic radial flow ceases after significant further expansion and cooling, whence the surface radial velocity (its average value given by $\left <\beta _{\mathrm {T}}\right >$ in Fig. 7.24) approaches β _T ≈ 0.65. Both data sets again exhibit an indication of saturation, over the interval toward top SPS energy: the SPS plateau. This supports our above conjecture that radial flow is, predominantly, a consequence of isentropic bulk hadronic expansion in this energy domain, which sets in at T _H. At RHIC energy, both parameters exhibit a further rise, suggesting that primordial partonic flow begins to contribute significantly to radial flow.

Fig. 7.24

Hadron decoupling temperature T _f, and average radial flow velocity $\left <\beta _{\mathrm {T}} \right >$ extracted from blast wave model (see Eq. (7.25)) fits of m _T spectra vs. $\sqrt {s}$ [54]

7.3 Hadronization and Hadronic Freeze-Out in A+A Collisions

Within the course of the global expansion of the primordial reaction volume the local flow “cells” will hit the parton-hadron phase boundary as their energy density approaches 𝜖 _crit ≈ 1 GeV/fm³. Hadronization will thus occur, not at an instant over the entire interaction volume, but within a finite overall time interval [86] that results from the spread of proper time at which individual cells, or coherent clusters of such cells (as developed during expansion) arrive at the phase boundary. However, irrespective of such a local-temporal occurrence, the hadronization process (which is governed by non perturbative QCD at the low Q ² corresponding to bulk hadronization) universally results in a novel, global equilibrium property that concerns the relative abundance of produced hadrons and resonances. This so-called “hadrochemical equilibrium state” is directly observable, in contrast to the stages of primordial parton equilibration that are only indirectly assessed, via dynamical model studies.

This equilibrium population of species occurs both in elementary and nuclear collisions [107]. We have seen in Fig. 7.17 a first illustration, by e ⁺e ⁻ annihilation data at $\sqrt {s}=91.2$ GeV LEP energy, that are well reproduced by the partition functions of the statistical hadronization model (SHM) in its canonical form [84]. The derived hadronization temperature, T _H = 165 MeV, turns out to be universal to all elementary and nuclear collision processes at $\sqrt {s} \ge 20$ GeV, and it agrees with the limiting temperature predicted by Hagedorn [38] to occur in any multi-hadronic equilibrium system once the energy density approaches about 0.6 GeV/fm³. Thus, the upper limit of hadronic equilibrium density corresponds, closely, to the lower limit, 𝜖 _crit = 0.6–1.0 GeV/fm³ of partonic equilibrium matter, according to lattice QCD [48]. In elementary collisions only about 20 partons or hadrons participate: there should be no chance to approach thermodynamic equilibrium of species by rescattering cascades, neither in the partonic nor in the hadronic phase. The fact that, nevertheless, the hadron formation temperature T _H coincides with the Hagedorn limiting temperature and with the QCD confinement temperature, is a consequence of the non-perturbative QCD hadronization process itself [85], which “gives birth” to hadrons/resonances in canonical equilibrium, at high $\sqrt {s}$, as we shall see below. This process also governs A+A collisions but, as it occurs here under conditions of high energy density extended over considerable volume, the SHM description now requires a grand canonical ensemble, with important consequences for production of strange hadrons (strangeness enhancement).

The grand canonical order of hadron/resonance production in central A+A collisions, and its characteristic strangeness enhancement shows that a state of extended matter that is quantum mechanically coherent must exist at hadronization [87, 88, 107]. Whether or not it also reflects partonic equilibrium properties (including flavor equilibrium), that would allow us to claim the direct observation of a quark gluon plasma state near T _c, cannot be decided on the basis of this observation alone, as the hadronization process somehow generates, by itself, the observed hadronic equilibrium. This conclusion, however, is still the subject of controversy [107].

Two typical examples of grand canonical SHM application are illustrated in Figs. 7.25 and 7.26, the first showing total hadron multiplicities in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV by NA49 [100] confronted with SHM predictions by Becattini et al. [19]. This plot is similar to Fig. 7.17 in which e ⁺e ⁻ annihilation to hadrons is confronted with a SHM prediction derived from the canonical ensemble [84]. Central Au+Au collision data at $\sqrt {s}=200$ GeV from several RHIC experiments are compared to grand canonical model predictions by Braun-Munzinger et al. [108] in Fig. 7.26. The key model parameters, T _H and the baryo-chemical potential μ _B result as 159 MeV (160 MeV), and 247 MeV (20 MeV) at $\sqrt {s}=17.3 \: (200)$ GeV, respectively. The universality of the hadronization temperature is obvious from comparison of the present values with the results of the canonical procedure employed in e ⁺e ⁻ annihilation to hadrons at $\sqrt {s}=91.2$ GeV (Fig. 7.17), and in canonical SHM fits [109] to p+p collision data at $\sqrt {s}=27.4$ GeV where T _H = 159 and 169 MeV, respectively.

Fig. 7.25

Total hadron multiplicities in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV [100] versus prediction of the grand canonical statistical hadronization model [19]

Fig. 7.26

Hadron multiplicity ratios at mid-rapidity in central Au+Au collisions at $\sqrt {s}=200$ GeV from RHIC experiments STAR, PHENIX and BRAHMS, compared to predictions of the grand canonical statistical model [108]

Figures 7.25 and 7.26 illustrate two different approaches employed in grand canonical SHM application, the former addressing the values of the hadronic multiplicities as obtained in approximate full 4π acceptance (within limitations implied by detector performance), the latter employing a set of multiplicity ratios obtained in the vicinity of mid-rapidity as invited, at RHIC energy, by the limited acceptance of the STAR and PHENIX experiments. The latter approach is appropriate, clearly, in the limit of boost-invariant rapidity distributions where hadron production ratios would not depend on the choice of the observational rapidity interval. We have shown in Sect. 7.2.2 that such conditions do, in fact, set in at top RHIC energy, as referred to in Fig. 7.26. However, at low $\sqrt {s}$ the y-distributions are far from boost-invariant, and the total rapidity gap Δy may become comparable, in the extreme case, to the natural rapidity widths of hadrons emitted in the idealized situation of a single, isotropically decaying fireball positioned at mid-rapidity. Its rapidity spectra, Eq. (7.5), resemble Gaussians with widths Γ_i ≈ 2.35 (T∕m _i)^1∕2 for hadron masses m _i. Clearly, the particle ratios (dN _i∕dy)∕(dN _j∕dy) then depend strongly on the position of the rapidity interval dy: away from y = 0 heavy hadrons will be strongly suppressed, and particle yields in narrow rapidity intervals are useless for a statistical model analysis unless it is known a priori that the radiator is a single stationary spherical fireball [110]. This is not the case toward top SPS energy (see Fig. 7.10), due to significant primordial longitudinal expansion of the hadron emitting source. Given such conditions, the total multiplicity per collision event (the invariant yield divided by the total overall inelastic cross section) should be employed in the SHM analysis, as is exemplified in Fig. 7.25.

7.3.1 Hadronic Freeze-Out from Expansion Flow

The hadronic multiplicities result from integration of the invariant triple differential cross section over p _T and y. Instrumental, experiment-specific conditions tend to result in incomplete p _T and/or y acceptances. It is important to ascertain that the effects of hydrodynamic transverse and longitudinal flow do not blast a significant part of the total hadron yield to outside the acceptance, and that they, more generally, do not change the relative hadron yield composition, thus basically affecting the SHM analysis. To see that hadronization incorporates only the internal energy in the co-moving frame [110], we first assume that hadrochemical freeze-out occurs on a sharp hypersurface Σ, and write the total yield of particle species i as

$$\displaystyle \begin{aligned} N_i=\int \frac{{\mathrm{d}}^3p}{E} \int_\Sigma \: p^{\mu} \; {\mathrm{d}}^3 \sigma_{\mu} (x)\: f_i (x,p)= \int_{\Sigma} {\mathrm{d}}^3 \sigma_{\mu} (x) j_i^{\mu} (x) {} \end{aligned} $$

(7.26)

where d³σ is the outward normal vector on the surface, and

$$\displaystyle \begin{aligned} j_i^{\mu}(x) = g_i \int {\mathrm{d}}^{4}p \; 2 \Theta (p^0) \delta(p^2-m^2_i) \: p^{\mu}(\exp \: [p \cdot u(x)-\mu_i]/T \pm 1)^{-1} {} \end{aligned} $$

(7.27)

is the grand canonical number current density of species i, μ _i the chemical potential, u(x) the local flow velocity, and g _i the degeneracy factor. In thermal equilibrium it is given by

$$\displaystyle \begin{aligned} \begin{array}{rcl} j_i^{\mu}(x)&\displaystyle = &\displaystyle \rho_i(x) u^{\mu}(x) \: \: \mbox{with} \\ \rho_i(x) &\displaystyle = &\displaystyle u_{\mu}(x) j_i^{\mu}(x) = \int {\mathrm{d}}^4 p \; 2 \Theta (p^0)\delta (p^2-m_i^2) \: p \cdot u(x) \: f_i (p \cdot u (x); T; \mu_i) \\ &\displaystyle = &\displaystyle \int {\mathrm{d}}^3 p^{\prime} \; f_i(E_{p^{\prime}}; T, \mu_i)=\rho_i(T, \mu_i). {} \end{array} \end{aligned} $$

(7.28)

Here $E_{p^{\prime }}$ is the energy in the local rest frame at point x. The total particle yield of species i is therefore

$$\displaystyle \begin{aligned} N_i=\rho_i (T, \mu_i) \int_\Sigma {\mathrm{d}}^3 \sigma_{\mu}(x) u^{\mu}(x) = \rho_i (T,\mu_i)\: V_{\Sigma}(u^{\mu}) {} \end{aligned} $$

(7.29)

where only the total comoving volume V _Σ of the freeze-out hypersurface Σ depends on the flow profile u ^μ. V  is thus a common total volume factor at hadronization (to be determined separately), and the flow pattern drops out from the yield distribution over species in 4π acceptance [110]. For nuclear collisions at SPS energies and below one thus should perform a SHM analysis of the total, 4π-integrated hadronic multiplicities, as was done in Fig. 7.25.

We note that the derivation above illustrates the termination problem of the hydrodynamic description of A+A collisions, the validity of which depends on conditions of a short mean free path, λ < 1 fm. A precise argumentation suggests that two different free paths are relevant here, concerning hadron occupation number and hadron spectral freeze-out, respectively. As hadrochemical freeze-out occurs in the immediate vicinity of T _c (and T _H ≈ 160–165 MeV from Figs. 7.25 and 7.26), the hadron species distribution stays constant throughout the ensuing hadronic phase, i.e. the “chemical” mean free path abruptly becomes infinite at T _H, whereas elastic and resonant rescattering may well extend far into the hadronic phase, and so does collective pressure and flow. In fact we have seen in Sect. 7.2.6 that the decoupling from flow occurs at T _F as low as 90–100 MeV (Fig. 7.24). Thus the hydrodynamic evolution of high $\sqrt {s}$ collisions has to be, somehow artificially, stopped at the parton-hadron boundary in order to get the correct hadron multiplicities N _i, of Eqs. (7.26)–(7.29), which then stay frozen-out during the subsequent hadronic expansion.

Equations (7.26)–(7.29) demonstrate the application of the Cooper-Frye prescription [111] for termination of the hydrodynamic evolution. The hyper-surface Σ describes the space-time location at which individual flow cells arrive at the freeze-out conditions, 𝜖 = 𝜖 _c and T = T _c, of hadronization. At this point, the resulting hadron/resonance spectra (for species i) are then given by the Cooper-Frye formula

$$\displaystyle \begin{aligned} E \;\frac{{\mathrm{d}} N_i}{{\mathrm{d}} ^3p} = \frac{{\mathrm{d}} N_i}{{\mathrm{d}} y \, p_{\mathrm{T}} \;{\mathrm{d}} p_{\mathrm{T}}} = \frac{g_i}{(2 \pi)^3} \: \int_{\Sigma} f_i (p \cdot u(x),x) p \cdot {\mathrm{d}}^3 \sigma (x), {} \end{aligned} $$

(7.30)

where p ^μf _i d³σ _μ is the local flux of particle i with momentum p through the surface Σ. For the phase space distribution f in this formula one takes the local equilibrium distribution at hadronic species freeze-out from the grand canonical SHM

$$\displaystyle \begin{aligned} f_i (E,x) = [\exp \{(E_i - \mu_i(x))/T \} \pm 1]^{-1} {} \end{aligned} $$

(7.31)

boosted with the local flow velocity u ^μ(x) to the global reference frame by the substitution E → p ⋅ u(x). Fixing T = T _c (taken e.g. from lattice QCD) the hadron multiplicities N _i then follow from Eq. (7.29), and one compares to experiment, as in Figs. 7.25 and 7.26. In order now to follow the further evolution, throughout the hadronic rescattering phase, and to finally compare predictions of Eq. (7.30) to the observed flow data as represented by the various Fourier-terms of Eq. (7.20) one has to re-initialize (with hadronic EOS) the expansion from Σ(T _c) = 165 MeV) until final decoupling [96], at T ≈ 100 MeV, thus describing e.g. radial and elliptic flow.

Alternatively, one might end the hydrodynamic description at T = T _c and match the thus obtained phase space distribution of Eq. (7.30) to a microscopic hadron transport model of the hadronic expansion phase [95, 112]. This procedure is illustrated in Fig. 7.27 by an UrQMD [113] calculation of Bass and Dumitru [114] for central Au+Au collisions at top RHIC energy. We select here the results concerning the survival of the hadronic multiplicities N _i throughout the dynamics of the hadronic expansion phase, which we have postulated above, based on the equality of the hadronization temperatures, T _H ≈ 160 MeV, observed in e ⁺e ⁻ annihilation (Fig. 7.17), where no hadronic expansion phase exists, and in central collisions of A ≈ 200 nuclei (Figs. 7.25 and reffig:Figure26). In fact, Fig. 7.27 shows that the {N _i} observed at the end of the hadronic cascade evolution agree, closely, with the initial {N _i} as derived from a Cooper-Frye procedure (Eq. (7.29)) directly at hadronization. On the other hand, p _T spectra and radial flow observables change, drastically, during the hadronic cascade expansion phase.

Fig. 7.27

Modification of mid-rapidity hadron multiplicities in central Au+Au collisions at $\sqrt {s}=200$ GeV after chemical freeze-out at T = T _c. Squares show a hydrodynamic model prediction at T = T _c (without further interaction); circles show the result of an attached UrQMD hadronic cascade expansion calculation [114]

The hadronic multiplicity distribution {N _i}, arising from the hadronization process at high $\sqrt {s}$, freezes-out instantaneously also in A+A collisions, and is thus preserved throughout the (isentropic) hadronic expansion phase. It is thus directly measurable and, moreover, its hadrochemical equilibrium features lend themselves to an analysis within the framework of Hagedorn-type statistical, grand canonical models. As we shall show below, the outcome of this analysis is contained in a [T _H, μ _B] parameter pair that reflects the conditions of QCD matter prevailing at hadronization, at each considered $\sqrt {s}$. In fact, the [T, μ] points resulting from the SHM analysis exhibited in Figs. 7.25 and 7.26 (at $\sqrt {s} = 17.3$ and 200 GeV, respectively) have been shown in the QCD matter phase diagram of Fig. 7.1 to approach, closely, the parton-hadron phase coexistence line predicted by lattice QCD. Thus, T _H ≈ T _c at high $\sqrt {s}$: hadrochemical freeze-out occurs in the immediate vicinity of QCD hadronization, thus providing for a location of the QCD phase boundary.

7.3.2 Grand Canonical Strangeness Enhancement

The statistical model analysis [19, 107, 108] of the hadronization species distribution N _i in A+A collisions is based on the grand canonical partition function for species i,

$$\displaystyle \begin{aligned} \ln Z_i= \frac{g_i V}{6 \pi^2 T} \: \int^{\infty}_0 \: \frac{k^4 \;{\mathrm{d}}k}{E_i (k) \exp \left\{(E_i (k) - \mu_i)/T \right\} \pm 1} {} \end{aligned} $$

(7.32)

where $E_i^2=k^2+m^2_i$, and $\mu _i \equiv \mu _{\mathrm {B}} B_i + \mu _s S_i + \mu _I I_3^i$ is the total chemical potential for baryon number B, strangeness S and isospin 3-component I ₃. Its role in Eq. (7.32) is to enforce, on average over the entire hadron source volume, the conservation of these quantum numbers. In fact, making use of overall strangeness neutrality (∑_iN _iS _i = 0) as well as of conserved baryon number (participant Z + N) and isospin (participant (N − Z)∕Z) one can reduce μ _i to a single effective potential μ _B. Hadronic freeze-out is thus captured in three parameters, T, V  and μ _B. The density of hadron/resonance species i then results as

$$\displaystyle \begin{aligned} n_i=\frac{T}{V} \frac {\delta}{\delta_{\mu}} \: \ln Z_i {} \end{aligned} $$

(7.33)

which gives

$$\displaystyle \begin{aligned} N_i=Vn_i=\frac{g_i V}{(2 \pi)^2} \: \int^{\infty}_0 \frac{k^2 \;{\mathrm{d}}k}{\exp \left\{(E_i(k)- \mu_i)/T \right\} \pm 1}. {} \end{aligned} $$

(7.34)

We see that the common freeze-out volume parameter is canceled if one considers hadron multiplicity ratios, N _i∕N _j, as was done in Fig. 7.26. Integration over momentum yields the one-particle function

$$\displaystyle \begin{aligned} N_i= \frac{VTg_i}{2 \pi^2} \: m_i^2 \: \sum_{n=1}^{\infty} \: \frac{(\pm 1)^{n+1}}{n} \: K_2 \left(\frac{nm_i}{T}\right) \exp \left( \frac {n \mu_i}{T} \right) {} \end{aligned} $$

(7.35)

where K ₂ is the modified Bessel function. At high T the effects of Bose or Fermi statistics (represented by the ± 1 term in the denominators of Eqs. (7.32) and (7.34)) may be ignored, finally leading to the Boltzmann approximation

$$\displaystyle \begin{aligned} N_i= \frac{VTgi}{2 \pi^2} \: m_i^2 \: K_2 \left(\frac{m_i}{T}\right) \exp \left( \frac {\mu_i}{T} \right) {} \end{aligned} $$

(7.36)

which is the first term of Eq. (7.35). This approximation is employed throughout the SHM analysis. It describes the primary yield of hadron species i, directly at hadronization. The abundance of hadronic resonance states is obtained convoluting equation (7.34) with a relativistic Breit-Wigner distribution [19]. Finally, the overall multiplicity, to be compared to the data, is determined as the sum of the primary multiplicity equation (7.36) and the contributions arising from the unresolved decay of heavier hadrons and resonances:

$$\displaystyle \begin{aligned} N_i^{\text{observed}}= N_i^{\text{primary}} + \sum_j {\mathrm{Br}} (j \rightarrow i) \:N_j. {} \end{aligned} $$

(7.37)

After having exposed the formal gear of grand canonical ensemble analysis we note that Eq. (7.36) permits a simple, first orientation concerning the relation of T to μ _B in A+A collisions by considering, e.g., the antiproton to proton production ratio. From Eq. (7.36) we infer the simple expression

$$\displaystyle \begin{aligned} N (\overline{p})/N(p) = \exp (-2 \mu_{\mathrm{B}}/T). {} \end{aligned} $$

(7.38)

Taking the mid-rapidity value 0.8 for $\overline {p}/p$ (from Fig. 7.26) at top RHIC energy, and assuming that hadronization occurs directly at the QCD phase boundary, and hence T ≈ T _c ≈ 165 MeV, we get μ _B ≃ 18 MeV from Eq. (7.38), in close agreement with the result, μ _B = 20 MeV, obtained [108] from the full SHM analysis. Equation (7.38) illustrates the role played by μ _B in the grand canonical ensemble. It logarithmically depends on the ratio of newly created quark-antiquark pairs (the latter represented by the $\bar {p}$ yield), to the total number of quarks including the net baryon number-carrying valence quarks (represented by the p yield).

The most outstanding property of the hadronic multiplicities observed in central A+A collisions is the enhancement of all strange hadron species, by factors ranging from about 2 to 20, as compared to the corresponding production rates in elementary hadron-hadron (and e ⁺e ⁻ annihilation) reactions at the same $\sqrt {s}$. I.e. the nuclear collision modifies the relative strangeness output by a “nuclear modification factor”, $R_s^{\text{AA}}=N_s^{\text{AA}}/0.5 \: N_{\text{part}}\: \cdot \: N_s^{pp}$, which depends on $\sqrt {s}$ and N _part and features a hierarchy with regard to the strangeness number s = 1, 2, 3 of the considered species, $R^{\text{AA}}_{s=1} < R^{\text{AA}}_{s=2} < R^{\text{AA}}_{s=3}$. These properties are illustrated in Figs. 7.28 and 7.29. The former shows the ratio of total K ⁺ to positive pion multiplicities in central Au+Au/Pb+Pb collisions, from lower AGS to top RHIC energies, in comparison to corresponding ratios from minimum bias p+p collisions [100]. We have chosen this ratio, instead of $\left <K^+\right >/N_{\text{part}}$, because it reflects, rather directly, the “Wroblewski ratio” of produced strange to non-strange quarks [107], contained in the produced hadrons,

$$\displaystyle \begin{aligned} \lambda_s \equiv \frac {2(\left<s\right>+\left<\overline{s}\right>)}{\left<u\right>+\left<d\right>+\left<\overline{u}\right>+\left<\overline{d}\right>} \approx \begin{cases} 0.2\ \text{in } \text{pp} \\ 0.45\ \text{in } \text{AA}. \end{cases} {} \end{aligned} $$

(7.39)

The low value of λ _s in pp (and all other elementary) collisions reflects a quark population far away from u, d, s flavor equilibrium, indicating strangeness suppression [109].

Fig. 7.28

The ratio of total K ⁺ to total π ⁺ multiplicity as a function of $\sqrt {s}$, in central Au+Au and Pb+Pb collisions and in p+p minimum bias collisions [100]

Fig. 7.29

The nuclear modification factors $R^{\text{AA}}_{s=1,2,3}$ for hyperon and anti-hyperon production in nucleus-nucleus collisions at $\sqrt {s}=17.3$ GeV, relative to the p+p reference at the same energy scaled by N _W(= N _part). The NA49 data refer to total 4π yields [116]. Closed lines represent the inverse strangeness suppression factors from ref. [119], at this energy

The so-called strangeness enhancement property of A+A collisions (obvious from Figs. 7.28 and 7.29) is, thus, seen as the removal of strangeness suppression; it is also referred to as a strangeness saturation, in SHM analysis [107, 108], for the reason that λ _s ≈ 0.45 corresponds to the grand canonical limit of strangeness production, implicit in the analysis illustrated in Figs. 7.25 and 7.26. The average $R^{\text{AA}}_{s=1}$ at $\sqrt {s} \ge 10$ GeV thus is about 2.2, both in the data of Fig. 7.28 and in the statistical model. It increases (Fig. 7.29) toward about 10 in s = 3 production of Ω hyperons.

In order to provide for a first guidance concerning the above facts and terminology regarding strangeness production we propose an extremely naive argument, based on the empirical fact of a universal hadronization temperature (Figs. 7.17, 7.25, and 7.26) at high $\sqrt {s}$. Noting that $\left <s\right >=\left <\overline {s}\right >$ and $\left <u\right >\approx \left <\overline {u}\right > \approx \left <d\right >\approx \left <\overline {d}\right >$ in a QGP system at μ _B near zero, and T = 165 MeV, just prior to hadronization, $\lambda _s \approx \left <s\right >/\left <u\right >\approx \exp \{(m_u - m_s)/T\} = 0.45$ at p _T → 0 if we take current quark masses, m _s − m _u ≈ 130 MeV. I.e. the value of λ _s in A+A collisions at high $\sqrt {s}$ resembles that of a grand canonical QGP at μ _B → 0, as was indeed shown in a 3 flavor lattice QCD calculation [115] at T ≈ T _c. On the contrary, a p+p collision features no QGP but a small fireball volume, at T ≈ T _c, within which local strangeness neutrality, $\left <s\right >=\left <\overline {s}\right >$ has to be strictly enforced, implying a canonical treatment [109]. In our naive model the exponential penalty factor thus contains twice the strangeness quark mass in the exponent, λ _s in pp collisions $\approx \exp \{2(m_u-m_s)/T \} \approx 0.2$, in agreement with the observations concerning strangeness suppression, which are thus referred to as canonical suppression. In a further extension of our toy model, now ignoring the u, d masses in comparison to m _s ≈ 135 MeV, we can estimate the hierarchy of hyperon enhancement in A+A collisions,

$$\displaystyle \begin{aligned} R^{\text{AA}}_s \propto N_s^{\text{AA}}/N_s^{pp} \cdot 0.5 \ N_{\text{part}} \approx \exp \{(-sm_s + 2sm_s)/T \} = 2.2, \: 5.1, \: 11.6 {} \end{aligned} $$

(7.40)

for s = 1, 2, 3, respectively. Figure 7.29 shows that these estimates correspond well with the data [116] for R ^AA derived in 4π acceptance for Λ,  Ξ and  Ω as well as for their antiparticles, from central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV. The p+p reference data, and C+C, Si+Si central collisions (obtained by fragmentation of the SPS Pb beam) refer to separate NA49 measurements at the same energy.

The above, qualitative considerations suggest that the relative strangeness yields reflect a transition concerning the fireball volume (that is formed in the course of a preceding dynamical evolution) once it enters hadronization. Within the small volumes, featured by elementary collisions (see Sect. 7.3.3), phase space is severely reduced by the requirement of local quantum number conservation [109, 117] including, in particular, local strangeness neutrality. These constraints are seen to be removed in A+A collisions, in which extended volumes of high primordial energy density are formed. Entering the hadronization stage, after an evolution of expansive cooling, these extended volumes will decay to hadrons under conditions of global quantum mechanical coherence, resulting in quantum number conservation occurring, non-locally, and on average over the entire decaying volume. This large coherent volume decay mode removes the restrictions, implied by local quantum number balancing. In the above, naive model we have thus assumed that the hadronization of an Omega hyperon in A+A collisions faces the phase space penalty factor of only three s quarks to be gathered, the corresponding three $\overline {s}$ quarks being taken care of elsewhere in the extended volume by global strangeness conservation. In the framework of the SHM this situation is represented by the grand canonical ensemble (Eqs. (7.34), (7.36)); the global chemical potential μ _B expresses quantum number conservation on average. Strict, local conservation is represented by the canonical ensemble.

The grand canonical (GC) situation can be shown to be the large collision volume limit (with high multiplicities {N _i}) of the canonical (C) formulation [118, 119], with a continuous transition concerning the degree of canonical strangeness suppression [119]. To see this one starts from a system that is already in the GC limit with respect to baryon number and charge conservation whereas strangeness is treated canonically. Restricting to s = 1 and − 1 the GC strange particle densities can be written (from Eq. (7.36)) as

$$\displaystyle \begin{aligned} n_{s=\pm 1}^{\mathrm{GC}} = \frac {Z_{s=\pm 1}}{V} \: \lambda ^{\pm 1}_s {} \end{aligned} $$

(7.41)

with

$$\displaystyle \begin{aligned} Z_{s=\pm 1}= \frac {Vg_s}{2 \pi^2} \: m_s^2 \: K_2 \: (\frac{m_s}{T}) \: \exp \Big\{(B_s \mu_{\mathrm{B}} + Q_s \mu_Q)/T \Big\} {} \end{aligned} $$

(7.42)

and a “fugacity factor” $\lambda _s^{\pm 1}= \exp \: (\mu _s/T)$. The canonical strange particle density can be written as [119]

$$\displaystyle \begin{aligned} n_s^C = n_s^{\mathrm{GC}} \cdot (\tilde{\lambda_{\mathrm{s}}}) {} \end{aligned} $$

(7.43)

with an effective fugacity factor

$$\displaystyle \begin{aligned} \tilde{\lambda_s} \: = \: \frac{S_{\pm 1}}{\sqrt{S_1 S_{-1}}} \: \frac{I_1(x)}{I_0(x)} {} \end{aligned} $$

(7.44)

where S _±1 =∑_s=±1Z _s=±1 is the sum over all created hadrons and resonances with s = ±1, the I _n(x) are modified Bessel functions, and $x=2 \sqrt {S_1 S_{-1}}$ is proportional to the total fireball volume V . In the limit x ≈ V →∞ the suppression factor I ₁(x)∕I ₀(x) → 1, and the ratio $S_{\pm 1}/\sqrt {S_1 S_{-1}}$ corresponds exactly to the fugacity λ _s in the GC formulation (see Eq. (7.41)). Thus the C and GC formulations are equivalent in this limit, and the canonical strangeness suppression effect disappears. Upon generalization to the complete strange hadron spectrum, with s = ±1, ±2, ±3, the strangeness suppression factor results [119] as

$$\displaystyle \begin{aligned} \eta(s) = I_s(x)/I_0(x). {} \end{aligned} $$

(7.45)

In particular for small x (volume), η(s) → (x∕2)^s, and one expects that the larger the strangeness content of the particle the smaller the suppression factor, and hence the larger the enhancement in going from elementary to central A+A collisions. This explains the hierarchy addressed in Eq. (7.40), and apparent from the data shown in Fig. 7.29. In fact, the curves shown in this figure represent the results obtained from Eq. (7.45), for s = 1, 2, 3 hyperon production at $\sqrt {s}=17.3$ GeV [119]. They are seen to be in qualitative agreement with the data. However the scarcity of data, existing at top SPS energy for total hyperon yields, obtained in 4π acceptance (recall the arguments in Sect. 7.3.1) both for A+A and p+p collisions does not yet permit to cover the SHM strangeness saturation curves in detail, for s > 1.

This saturation is seen in Fig. 7.29, to set in already at modest system sizes, but sequentially so, for ascending hyperon strangeness. Note that SHM saturation is sequentially approached, from Eq. (7.45), with increasing fireball volumeV . In order to make contact to the experimental size scaling with centrality, e.g. N _part, the model of ref. [119], which is illustrated in Fig. 7.29, has converted the genuine volume scale to the N _part scale by assuming a universal eigenvolume of 7 fm³ per participant nucleon. I.e. N _part = 10 really means a coherent fireball volume of 70 fm³, in Fig. 7.29. Within this definition, saturation of s = 1, 2, 3 sets in at fireball volumes at hadronization of about 60, 240 and 600 fm³, respectively: this is the real message of the SHM curves in Fig. 7.29.

The above direct translation of coherent fireball volume to participant number is problematic [120] as it assumes that all participating nucleons enter into a single primordially coherent fireball. This is, however, not the case [120] particularly in the relative small scattering systems that cover the initial, steep increase of η(s), where several local high density clusters are formed, each containing a fraction of N _part. This is revealed by a percolation model [120] of cluster overlap attached to a Glauber calculation of the collision/energy density. At each N _part an average cluster volume distribution results which can be transformed by Eq. (7.45) to an average {η(s, V )} distribution whose weighted mean is the appropriate effective canonical suppression factor corresponding to N _part. On the latter scale, the SHM suppression curve thus shifts to higher N _part, as is shown in Fig. 7.30 for the K ⁺∕π ⁺ ratio vs. N _part, measured at mid-rapidity by PHENIX in Au+Au collisions at $\sqrt {s}=200$ GeV, which is reproduced by the percolation model [120]. Also included is a prediction for Cu+Cu at this energy which rises more steeply on the common N _part scale because the collision and energy density reached in central Cu+Cu collisions, at N _part ≈ 100, exceeds that in peripheral Au+Au collisions (at the same N _part) which share a more prominent contribution from the dilute surface regions of the nuclear density profile. We note, finally, that this deviation from universal N _part scaling does not contradict the observations of a perfect such scaling as far as overall charged particle multiplicity densities are concerned (recall Fig. 7.12) which are dominated by pions, not subject to size dependent canonical suppression.

Fig. 7.30

The mid-rapidity K ⁺ to π ⁺ ratio vs. N _part in minimum bias Au+Au collisions at $\sqrt {s}=200$ GeV, compared to the percolation model [120] (solid line); a prediction of which for Cu+Cu at similar energy is given by the long dashed line (see text for detail)

7.3.3 Origin of Hadro-Chemical Equilibrium

The statistical hadronization model (SHM) is not a model of the QCD confinement process leading to hadrons, which occurs once the dynamical cooling evolution of the system arrives at T _c. At this stage the partonic reaction volume, small in elementary collisions but extended in A+A collisions, will decay (by whatever elementary QCD process) to on-shell hadrons and resonances. This coherent quantum mechanical decay results in a de-coherent quasi-classical, primordial on-shell hadron-resonance population which, at the instant of its formation, lends itself to a quasi-classical Gibbs ensemble description. Its detailed modalities (canonical for small decaying systems, grand canonical for extended fireballs in A+A collisions), and its derived parameters [T, μ _B] merely recast the conditions, prevailing at hadronization. The success of SHM analysis thus implies that the QCD hadronization process ends in statistical equilibrium concerning the hadron-resonance species population.

In order to identify mechanisms in QCD hadronization that introduce the hadro-chemical equilibrium we refer to jet hadronization in e ⁺e ⁻ annihilation reactions, which we showed in Fig. 7.17 to be well described by the canonical SHM. In di-jet formation at LEP energy, $\sqrt {s}=92$ GeV, we find a charged particle multiplicity of about 10 per jet, and we estimate that, likewise, about 10 primordial partons participate on either side of the back-to-back di-jet [85]. There is thus no chance for either a partonic or hadronic, extensive rescattering toward chemical equilibrium. However, in the jet hadronization models developed by Amati and Veneziano [83], Webber [121] and Ellis and Geiger [85] the period of QCD DGLAP parton shower evolution (and of perturbative QCD, in general) ends with local color neutralization, by formation of spatial partonic singlet clusters. This QCD “color pre-confinement” [83] process reminds of a coalescence mechanism, in which the momenta and the initial virtual masses of the individual clustering partons get converted to internal, invariant virtual mass of color neutral, spatially extended objects. Their mass spectrum [121] extends from about 0.5 to 10 GeV. This cluster mass distribution, shown in Fig. 7.31, represents the first stochastic element in this hadronization model.

Fig. 7.31

Invariant mass spectrum of color neutralization clusters in the Veneziano-Webber hadronization model [83, 121]

The clusters are then re-interpreted within non-perturbative QCD: their internal, initially perturbative QCD vacuum energy gets replaced by non-perturbative quark and gluon condensates, making the clusters appear like hadronic resonances. Their subsequent quantum mechanical decay to on-shell hadrons is governed by the phase space weights given by the hadron and resonance spectrum [85, 121]. I.e. the clusters decay under “phase space dominance” [85], the outcome being a micro-canonical or a canonical hadron and resonance ensemble [84, 107]. The apparent hadro-chemical equilibrium thus is the consequence of QCD color neutralization to clusters, and their quantum mechanical decay under local quantum number conservation and phase space weights. We note that the alternative description of hadronization, by string decay [122], contains a quantum mechanical tunneling mechanism, leading to a similar phase space dominance [123].

Hadronization in e ⁺e ⁻ annihilation thus occurs from local clusters (or strings), isolated in vacuum, of different mass but similar energy density corresponding to QCD confinement. These clusters are boosted with respect to each other but it was shown [124] that for a Lorentz invariant scalar, such as multiplicity, the contributions of each cluster (at similar T) can be represented by a single canonical system with volume equal to the sum of clusters. In the fit of Fig. 7.17 this volume sum amounts to about 45 fm³ [84]; the individual cluster volumes are thus quite small, of magnitude a few fm³ [85]. This implies maximum canonical strangeness suppression but may, in fact, require a micro-canonical treatment of strangeness [109], implying a further suppression. These MC effects are oftentimes included [125] in the canonical partition functions by an extra strangeness fugacity parameter γ _s < 1 which suppresses s = 1, 2, 3 in a hierarchical manner, $\left <N_i(s)\right >\approx (\gamma _s)^{s_i}$. The fit of Fig. 7.17 requires γ _s = 0.66, a value typical of canonical multiplicity analysis in p+p, p+$\overline {\mathrm {p}}$ and e ⁺e ⁻ annihilation collisions [109] at $\sqrt {s} \ge 30$ GeV.

The above picture, of hadrochemical equilibrium resulting from the combined stochastic features of QCD color neutralization by cluster formation, and subsequent quantum mechanical decay to the on-shell hadron and resonance spectrum (under phase space governance) lends itself to a straight forward extension to A+A collisions. The essential new features, of grand canonical hadronization including strangeness enhancement, should result from the fact that extended space-time volumes of 𝜖 > 𝜖 _crit are formed in the course of primordial partonic shower evolution, an overlap effect increasing both with $\sqrt {s}$ and with the size of the primordial interaction volume. As the volume of the elementary hadronization clusters amounts to several fm³ it is inevitable that the clusters coalesce, to form extended “super-cluster” volumes prior to hadronization [120]. As these super-clusters develop toward hadronization via non perturbative QCD dynamics, it is plausible to assume an overall quantum mechanical coherence to arise over the entire extended volume, which will thus decay to hadrons under global quantum number conservation, the decay products thus modeled by the GC ensemble.

Our expectation that space-time coalescence of individual hadronization clusters will lead to a global, quantum mechanically coherent extended super-cluster volume, that decays under phase space dominance, appears as an analogy to the dynamics and quantum mechanics governing low energy nuclear fission from a preceding “compound nucleus” [126]. Note that the observation of a smooth transition from canonical strangeness suppression to grand canonical saturation (Figs. 7.29, 7.30) lends further support to the above picture of a percolative growth [120] of the volume that is about to undergo hadronization.

An extended, coherent quark gluon plasma state would, of course, represent an ideal example of such a volume [127] and, in fact, we could imagine that the spatial extension of the plasma state results from a percolative overlap of primordial zones of high energy density, which becomes more prominent with increasing $\sqrt {s}$ and N _part. A QGP state preceding hadronization will thus lead to all the observed features. However, to be precise: the hadronizing QCD system of extended matter decaying quantum coherently, could still be a non-equilibrium precursor of the ideal equilibrium QGP, because we have seen above that hadrochemical equilibrium also occurs in e ⁺e ⁻ annihilation, where no partonic equilibrium exists. It gets established in the course of hadronization, irrespective of the degree of equilibrium prevailing in the preceding partonic phase.

7.3.4 Hadronization vs. Rapidity and $\sqrt {s}$

We have argued in Sect. 7.3.1 that, at relatively low $\sqrt {s}$, the total rapidity gap Δy does not significantly exceed the natural thermal rapidity spreading width Γ_i ≈ 2.35 (T∕m _i)^1∕2 of a single, isotropically decaying fireball, centered at mid-rapidity and emitting hadrons of mass m _i [110]. However, this procedure involves an idealization because in the real Pb+Pb collision the intersecting dilute surface sections of the nuclear density profiles will lead to a significant contribution of single-scattering NN collisions, outside the central high density fireball. The leading hadron properties of such “corona collisions” result in wider proper rapidity distributions, quite different from those of the central fireball decay hadrons. Their contribution will thus be prominent near target/projectile rapidity, and will feature a canonically suppressed strangeness. The one-fireball assumption, although inevitable at small Δy, does not quite resemble the physical reality. This may explain the need for an additional strangeness suppression factor in the GC one-particle partition function (Eq. (7.32)) that has, unfortunately, also been labeled γ _s but expresses physics reasons quite different from the extra suppression factor that reflects micro-canonical phase space constraints in elementary collisions. It turns out that all GC analysis of central A+A collisions at low $\sqrt {s}$, and addressed to total 4π multiplicities, requires a γ _s of 0.7–0.85 [19]; in the fit of Fig. 7.25γ _s = 0.84.

At RHIC, Δy ≈ 11 ≫ Γ_i, and such difficulties disappear: γ _s ≈ 1 at midrapidity and, moreover, the wide gap permits a SHM analysis which is differential in y. Figure 7.32 shows the y-dependence of the ratios π ⁻∕π ⁺, K ⁻∕K ⁺ and $\overline {p}/p$ as obtained by BRAHMS [128] in central Au+Au collisions at $\sqrt {s}=200$ GeV. The figure shows a dramatic dependence of the $\overline {p}/p$ ratio, which reflects the local baryochemical potential according to Eq. (7.38). At y _CM > 1 the $\overline {p}/p$ ratio drops down steeply, to about 0.2 at y ≈ 3.5, thus making close contact to the top SPS energy value obtained by NA49 [129]. The K ⁻∕K ⁺ ratio follows a similar but weaker drop-off pattern, to about 0.65 again matching with the top SPS energy value of about 0.6 [130]. The deviation from unity of these ratios reflects the rapidity densities of initial valence u, d quarks, relative to the densities of newly created light and strange quark-antiquark pairs, i.e. the y distribution of the net baryon number density, and of the related baryo-chemical potential of the GC ensemble. Thus, in analyzing successive bins of the rapidity distributions in Fig. 7.32, the major variation in the GC fit concerns the baryo-chemical potential μ _B(y) which increases from about 20 MeV (Fig. 7.26) at mid-rapidity, to about 150 MeV at y ≥ 3 while the hadronization temperature stays constant, at T = 160 MeV. This interplay between $K^-/K^+, \: \overline {p}/p$ and μ _B is illustrated [128] in the right hand panel of Fig. 7.32, and shown to be well accounted for by the GC statistical model [131].

Fig. 7.32

(Left) Anti-hadron to hadron ratios as a function of rapidity in central Au+Au collisions at $\sqrt {s}=200$ GeV. (Right) Interpretation of the correlation between $\overline {p}/p$ and K ⁻∕K ⁺ in terms of baryo-chemical potential μ _B variation in the grand canonical statistical model. From [128]

These considerations imply that hadronization at RHIC (and LHC) energy occurs local in y-space and late in time. The density distribution of net baryon number results from the primordial pQCD shower evolution (c.f. Sect. 7.2.4), and is thus fixed at formation time, t ₀ ≤ 0.6 fm/c at RHIC. Hadronization of the bulk partonic matter occurs later, at t ≥ 3 fm/c [86, 95], and transmits the local conditions in rapidity space by preserving the local net baryon quantum number density. Most importantly we conclude that hadronization occurs, not from a single longitudinally boosted fireball but from a succession of “super-clusters”, of different partonic composition depending on y, and decaying at different time due to the Lorentz-boost that increases with y, in an “inside-outside” pattern (c.f. Fig. 7.18). We are thus witnessing at hadronization a Hubble expanding system of local fireballs. The detailed implications of this picture have not been analyzed yet. Note that a central RHIC collision thus does not correspond to a single hadronization “point” in the [T, μ] plane of Fig. 7.1 but samples {T, μ} along the QCD parton-hadron coexistence line [132].

Throughout this chapter we have discussed hadronic freeze-out at high $\sqrt {s}$ only (top SPS to RHIC energy), because of the proximity of the chemical freeze-out parameters [T, μ _B] to the QCD phase boundary from lattice QCD, which suggests an overall picture of hadronization, to occur directly from a partonic cluster or super-cluster. Our discussion of the GC statistical hadronization model has been explicitly or implicitly based on the assumption that hadronic freeze-out coincides with hadronization. However, the GC model has also been applied successfully to hadro-chemical freeze-out at $\sqrt {s}$ down to a few GeV [19, 107, 108] where it is not expected that the dynamical evolution traverses the phase boundary at all, but grand canonical multiplicity distributions, and their characteristic strangeness enhancement pattern, are observed throughout. Toward lower $\sqrt {s}, \: T$ decreases while μ _B increases, as is shown in Fig. 7.33 which presents a compilation of all reported freeze-out parameters [108].

Fig. 7.33

Energy dependence of the hadro-chemical freeze-out points obtained by grand canonical statistical model analysis in the plane [T, μ _B], with interpolating curve at fixed energy per particle of about 1 GeV [107, 139]

These points have also been included in the phase diagram of Fig. 7.1 which shows that they are gradually branching away from the phase separation boundary line that could recently be predicted by lattice QCD once new methods had been developed to extend the theory to finite μ _B [9, 10]. At $\sqrt {s} \ge 20$ GeV we see that

$$\displaystyle \begin{aligned} \epsilon_{\mathrm{c}} ({\text{QCD}}) \approx \epsilon_{\mathrm{H}} \approx \epsilon_{\mathrm{GC}} {} \end{aligned} $$

(7.46)

where 𝜖 _GC is the freeze-out density inferred from GC analysis [19, 107, 108].

In turn, the GC hadronic freeze-out points drop below the lattice QCD coexistence line at lower $\sqrt {s}$, implying that chemical freeze-out now occurs within the hadronic expansion phase. This requires a model of freeze-out, now governed by the properties of a high density hadronic medium, upon expansive cooling and dilution. Holding on to the model of a quantum mechanical de-coherence decay to on-shell hadrons that we discussed in Sect. 7.3.3, we argue that an initial, extended high density hadronic fireball, given sufficient life-time at T smaller, but not far below T _c, could also be seen as a quantum mechanically coherent super-cluster, as governed by effective mean fields [133]. In such a medium hadrons, at T near T _c, acquire effective masses and/or decay widths far off their corresponding properties in vacuum: they are off-shell, approaching conditions of QCD chiral symmetry restoration as T → T _c [134]. This symmetry is inherent in the elementary QCD Lagrangian, and “softly” broken within the light quark sector by the small non-zero current quark masses, but severely broken at T → 0 by the high effective constituent quark masses that get dressed by non perturbative QCD vacuum condensates. Pictorially speaking, hadrons gradually loose this dressing as T → T _c [135], introducing a change, away from in vacuum properties, in the hadronic mass and width spectrum. Such in-medium chiral restoration effects have, in fact, been observed in relativistic A+A collisions, by means of reconstructing the in-medium decay of the ρ vector meson to an observed e ⁺e ⁻ pair [136] (see Sect. 7.6.3).

A dense, high T hadronic system, with mean-field induced off-shell constituents is also, clearly, quantum mechanically coherent. At a certain characteristic density, 𝜖 < 𝜖 _c, and temperature T < T _c, as reached in the course of overall hadronic expansion, this extended medium will undergo a decoherence transition to classical on-shell hadrons. Its frozen-out hadronic multiplicity distribution should be, again, characterized by the phase space weights of a grand canonical ensemble at T < T _c. Theoretical studies of such a mean field hadronic expansion mode [137] have also shown that such mechanisms play essentially no role at $\sqrt {s} \ge 20$ GeV because the expanding system is already in rapid flow once it traverses the phase boundary, with an expansion time scale shorter than the formation time scale of mean field phenomena. At lower energies, on the other hand, the system might not even dive into the deconfined phase but spend a comparatively long time in its direct vicinity, at the turning point between compression and re-expansion where all dynamical time constants are large, and the hadron density is high, such that the inelastic hadronic transmutation rate becomes high (particularly in collisions of more than two hadronic reactants, with reaction rates [138] proportional to 𝜖 ⁿ), and sufficiently so for maintaining hadronic chemical equilibrium after it is first established at maximum hadron density, in low $\sqrt {s}$ systems that do not cross the phase boundary at all.

The GC freeze-out parameters [T, μ] at various $\sqrt {s}$ in Fig. 7.33 permit a smooth interpolation in the T, μ plane [139], which, in turn, allows for GC model predictions which are continuous in $\sqrt {s}$. Such a curve is shown in Fig. 7.28 compared to the 4π data points for the K ⁺∕π ⁺ multiplicity ratio in central collisions Au+Au/Pb+Pb, at all $\sqrt {s}$ investigated thus far. It exhibits a smooth maximum, due to the interplay of T saturation and μ _B fall-off to zero, but does not account for the sharp peak structure seen in the data at $\sqrt {s} \approx 7$ GeV and μ _B ≈ 480 MeV. This behavior is not a peculiarity of the K ⁺ channel only; it also is reflected in an unusually high Wroblewski ratio (see Eq. (7.39)) obtained at $\sqrt {s} = 7.6$ GeV, of λ _s = 0.60 [19]. This sharp strangeness maximum is unexplained as of yet. It implies that hadron formation at this $\sqrt {s}$ reflects influences that are less prominent above and below, and most attempts to understand the effect [141,142,143] are centered at the assumption that at this particular $\sqrt {s}$ the overall bulk dynamics will settle directly at the phase boundary where, moreover, finite μ _B lattice theory also expects a QCD critical point [9,10,11]. This would cause a softest point to occur in the equation of state, i.e. a minimum in the relation of expansion pressure vs. energy density, slowing down the dynamical evolution [144, 145], and thus increasing the sensitivity to expansion modes characteristic of a first order phase transition [143], which occurs at $\mu _{\mathrm {B}} \ge \mu _{\mathrm {B}}^{\mathrm {crit}}$. Such conditions may modify the K/π ratio (Fig. 7.28) [143].

It thus appears that the interval from top AGS to lower SPS energy, $5 \le \sqrt {s} \le 10$ GeV, promises highly interesting information regarding the QCD phase diagram (Fig. 7.1) in the direct vicinity of the parton-hadron coexistence line. In particular, the physics of a critical point of QCD matter deserves further study. Observable consequences also comprise so-called “critical fluctuations” [146, 147] of multiplicity density, mean transverse momentum and hadron-chemical composition [148], the latter in fact being observed near $\sqrt {s}=7$ GeV in an event by event study of the K∕π ratio in central Pb+Pb collisions [149]. We shall return to critical point physics in Sect. 7.7.

7.4 Elliptic Flow

We have up to now mostly stressed the importance of central collisions and mid-rapidity data because they provide for the highest primordial energy density and avoid problems caused by emission anisotropy and the presence of cold spectator sections of target and projectile nuclei. On the other hand, a fundamentally new window of observation is opened by non-central collisions as the finite impact parameter breaks cylinder symmetry, defining emission anisotropies with respect to the orientation of the impact vector $\vec {b}$ as we have shown in Eq. (7.20). In a strongly interacting fireball collision dynamics, the initial geometric anisotropy of the reaction volume gets transferred to the final momentum spectra and thus becomes experimentally accessible. Furthermore, the high charged particle multiplicity allows for an event-by-event determination of the reaction plane (direction of $\vec {b}$), enabling the study of observables at azimuth φ, relative to the known reaction plane. We shall show that this opens a window into the very early stages of A+A collisions onward from the end of nuclear interpenetration, at τ ≈ 2 R(A)∕γ _CM. Our observation thus begins at the extreme energy densities prevailing right at formation time (Sects. 7.2.4 and 7.2.5), i.e. concurrent with the initialization phase of relativistic hydrodynamic expansion. We access the phase diagram of Fig. 7.1 in regions far above the QCD phase boundary.

Before turning to the details of elliptic flow data we wish to illustrate [96] the above statements. Figure 7.34 exhibits the transverse projection of primordial energy density, assumed to be proportional to the number density of participant nucleons in the overlap volume arising from a Au+Au collision at impact parameter b = 7 fm. The nuclear density profiles (assumed to be of Woods-Saxon type) intersect in an ellipsoidal fireball, with minor axis along the direction of $\vec {b}$ which is positioned at y = 0. The obvious geometrical deformation can be quantified by the spatial excentricity (unfortunately also labeled 𝜖 in the literature)

$$\displaystyle \begin{aligned} \epsilon_x(b)=\frac{\left<y^2-x^2\right>}{\left<y^2+x^2\right>} {} \end{aligned} $$

(7.47)

where the averages are taken with respect to the transverse density profiles of Fig. 7.34. 𝜖 _x is zero for b = 0, reaching a value of about 0.3 in the case b = 7 fm illustrated in Fig. 7.34.

Fig. 7.34

Transverse projection of primordial binary collision density in an Au+Au collision at impact parameter 7 fm, exhibiting participant parton spatial excentricity [96]

Translated into the initialization of the hydrodynamic expansion the density anisotropy implies a corresponding pressure anisotropy. The pressure is higher in x than in y direction, and thus is the initial acceleration, leading to an increasing momentum anisotropy,

$$\displaystyle \begin{aligned} \epsilon_p(\tau)=\frac{\int {\mathrm{d}}x \;{\mathrm{d}}y \: (T^{xx}-T^{yy})}{\int {\mathrm{d}}x \;{\mathrm{d}}y \: (T^{xx}+T^{yy})} {} \end{aligned} $$

(7.48)

where $T^{\mu x}_{(x)}$ is the fluid’s energy-momentum tensor. Figure 7.35 shows [96, 150] the time evolution of the spatial and momentum anisotropies for the collision considered in Fig. 7.34, implementing two different equations of state which are modeled with (without) implication of a first order phase transition in “RHIC” (“EOS1”). A steep initial rise is observed for 𝜖 _p, in both cases: momentum anisotropy builds up during the early partonic phase at RHIC, while the spatial deformation disappears. I.e. the initial source geometry, which is washed out later on, imprints a flow anisotropy which is preserved, and observable as “elliptic flow”. A first order phase transition essentially stalls the buildup of 𝜖 _p at about τ = 3 fm/c when the system enters the mixed phase, such that the emerging signal is almost entirely due to the partonic phase. We have to note here that the “ideal fluid” (zero viscosity) hydrodynamics [150] employed in Fig. 7.35 is, at first, a mere hypothesis, in view also of the fact that microscopic transport models have predicted a significant viscosity, both for a perturbative QCD parton gas [92, 151] and for a hadron gas [95, 152]. Proven to be correct by the data, the ideal fluid description of elliptic flow tells us that the QGP is a non-perturbative liquid [153, 154].

Fig. 7.35

Time evolution of the spatial excentricity 𝜖 _x and the momentum space anisotropy 𝜖 _p (Eqs. (7.47) and (7.48)) in the hydrodynamic model of an Au+Au collision at b = 7 fm, occurring at $\sqrt {s}=200$ GeV [96]. The dynamics is illustrated with two equations of state

Elliptic flow is quantified by the coefficient v ₂ of the second harmonic term in the Fourier expansion (see Eq. (7.20)) of the invariant cross section; it depends on $\sqrt {s}$, b, y and p _T. Figure 7.36 shows the $\sqrt {s}$ dependence of v ₂ at mid-rapidity and averaged over p _T, in Au+Au/Pb+Pb semi-peripheral collisions [93, 155]. We see that the momentum space anisotropy is relatively small overall, but exhibits a steep rise toward top RHIC energy.

Fig. 7.36

Energy dependence of the elliptic flow parameter v ₂ at mid-rapidity and averaged over p _T, in Au+Au and Pb+Pb semi-peripheral collisions [155]

Figure 7.37 shows the (pseudo)-rapidity dependence of v ₂ at $\sqrt {s}=130$ and 200 GeV as obtained by PHOBOS [156] for charged particles in minimum bias Au+Au collisions. It resembles the corresponding charged particle rapidity density distribution of Fig. 7.8, suggesting that prominent elliptic flow arises only at the highest attainable primordial energy density.

Fig. 7.37

Pseudo-rapidity dependence of the p _T-averaged elliptic flow coefficient v ₂ for charged hadrons at $\sqrt {s}=130$ and 200 GeV [156]

That such conditions are just reached at top RHIC energy is shown in Figs. 7.38 and 7.39. The former combines STAR [157] and PHENIX [158] data for the p _T dependence of elliptic flow, observed for various identified hadron species π ^±, K ^±, p, K ⁰ and $\Lambda , \overline {\Lambda }$ in Au+Au at 200 GeV. The predicted hydrodynamic flow pattern [96, 159] agrees well with observations in the bulk p _T < 2 GeV/c domain. Figure 7.39 (from [155]) unifies average v ₂ data from AGS to top RHIC energies in a scaled representation [93] where v ₂ divided by the initial spatial anisotropy 𝜖 _x is plotted versus charged particle mid-rapidity density per unit transverse area S, the latter giving the density weighted transverse surface area of primordial overlap, Fig. 7.34. Figure 7.39 includes the hydrodynamic predictions [95, 96, 150, 159, 161] for various primordial participant or energy densities as implied by the quantity (1∕S) dn _ch∕dy [93]. Scaling v ₂ by 𝜖 _x enhances the elliptic flow effect of near-central collisions where 𝜖 _x is small, and we see that only such collisions at top RHIC energy reach the hydrodynamical ideal flow limit in models that include an EOS ansatz which incorporates [96] the effect of a first order phase transition, which reduces the primordial flow signal as was shown in Fig. 7.35.

Fig. 7.38

Transverse momentum dependence of elliptic flow v ₂ for mesons and baryons in Au+Au collisions at $\sqrt {s}=200$ GeV. The hydrodynamic model [96, 159] describes the mass dependence at p _T ≤ 2 GeV/c

Fig. 7.39

Elliptic flow v ₂ scaled by spatial excentricity 𝜖 as a function of charged particle density per unit transverse area S, from AGS to top RHIC energy. The hydrodynamic limit is only attained at RHIC [155]

At top RHIC energy, the interval between t ₀ ≈ 0.6 fm/c, and hadronization time, t _H ≈ 3 fm/c, is long enough to establish dynamical consequences of an early approach toward local equilibrium. The “lucky coincidence” of such a primordial resolution of dynamical time scale, with the extreme primordial density, offered by semi-central collisions of heavy nuclei, results in an extremely short mean free path of the primordial matter constituents, thus inviting a hydrodynamic description of the expansive evolution. Consistent application of this model reveals a low viscosity: the primordial matter resembles an ideal fluid, quite different from earlier concepts, of a weakly interacting partonic gas plasma state (QGP) governed by perturbative QCD screening conditions [36, 41].

A further, characteristic scaling property of elliptic flow is derived from the p _T dependence of v ₂, observed for the different hadronic species. In Fig. 7.38 one observes a hadron mass dependence, the v ₂ signal of pions and charged kaons rising faster with p _T than that of baryons. Clearly, within a hydrodynamic flow velocity field entering hadronization, heavier hadronic species will capture a higher p _T, at a given flow velocity. However, unlike in hadronic radial expansion flow phenomena (c.f. Sect. 7.2.6) it is not the hadronic mass that sets the scale for the total p _T derived, per particle species, from the elliptic flow field, but the hadronic valence quark content. This conclusion is elaborated [94] in Fig. 7.40.

Fig. 7.40

v ₂ vs. p _T (left panel) and transverse kinetic energy KE _T = m _T − m ₀ (middle) for several hadronic species in min. bias Au+Au collisions at $\sqrt {s}=200$ GeV, showing separate meson and baryon branches. Scaling (right panel) is obtained by valence quark number n _q, dividing v ₂ and KE _T [94]

The left panel shows measurements of the p _T dependence of v ₂ for several hadronic species, in minimum bias Au+Au collisions at $\sqrt {s}=200$ GeV [161]. The middle panel bears out the hydrodynamically expected [162] particle mass scaling when v ₂ is plotted vs. the relativistic transverse kinetic energy KE _T ≡ m _T − m where $m_{\mathrm {T}}=(p_{\mathrm {T}}^2+m^2)^{1/2}$. For KE _T ≥ 1 GeV, clear splitting into a meson branch (lower v ₂) and a baryon branch (higher v ₂) occurs. However, both of these branches show good scaling separately. The right panel shows the result obtained after scaling both v ₂ and KE _T (i.e. the data in the middle panel) by the constituent quark number, n _q = 2 for mesons and n _q = 3 for baryons. The resulting perfect, universal scaling is an indication of the inherent quark degrees of freedom in the flowing matter as it approaches hadronization. We thus assert that the bulk of the elliptic flow signal develops in the pre-hadronization phase.

The above scaling analysis has been extended to Φ meson and Ω hyperon production, and also to first PHENIX results [163] concerning elliptic flow of the charmed D meson [94], with perfect agreement to the observations made in Fig. 7.40, of a separation into meson/hadron branches on the KE _T scale, which merge into a universal v ₂ scaling once both v ₂ and KE _T per valence quark are considered. The observation that the D meson charm quark apparently shares in the universal flow pattern is remarkable as its proper relaxation time is, in principle, lengthened by a factor M∕T [164]. A high partonic rescattering cross section σ is thus required in the primordial QGP fireball, to reduce the partonic mean free path λ = 1∕nσ (where n is the partonic density), such that λ ≪ A ^1∕3 (the overall system size) and, simultaneously, λ < 1 fm in order to conform with the near-zero mean free path implication of the hydrodynamic description of the elliptic flow, which reproduces the data gathered at RHIC energy. The presence of a high partonic rescattering cross section was born out in a parton transport model study [92] of the steep linear rise of the elliptic flow signal with p _T (Fig. 7.38). In such a classical Boltzmann equation approach the cross sections required for the system to translate the initial spatial into momentum space anisotropy, fast enough before the initial deformation gets washed out during expansion (c.f. Fig. 7.35), turn out to exceed by almost an order of magnitude the values expected in a perturbative QCD quark-gluon gas [92].

The non-perturbative quark-gluon plasma is thus a strongly coupled state (which has been labeled sQGP [165]). At RHIC energy this reduces the partonic mean free path to a degree that makes hydrodynamics applicable. A Navier-Stokes analysis [166] of RHIC flow data indicates that the viscosity of the QGP must be about ten times smaller than expected if the QGP were a weakly interacting pQCD Debye screened plasma. This justifies the use of perfect fluid dynamics.

Considering first attempts to derive a quantitative estimate of the dimensionless ratio of (shear) viscosity to entropy, we note that η∕s is a good way to characterize the intrinsic ability of a substance to relax toward equilibrium [167]. It can be estimated from the expression [94]

$$\displaystyle \begin{aligned} \eta/s \approx T \lambda_{\mathrm{f}} \: c_{\mathrm{s}} {} \end{aligned} $$

(7.49)

where T is the temperature, λ _f the mean free path, and c _s is the sound speed derived from the partonic matter EOS. A fit by the perfect fluid “Buda-Lund” model [168] to the scaled v ₂ data shown in Fig. 7.40 yields T = 165 ± 3 MeV; c _s is estimated as 0.35 ± 0.05 [94, 162], and λ _f ≈ 0.30 fm taken from a parton cascade calculation including 2 ↔ 3 scattering [169]. The overall result is [94]

$$\displaystyle \begin{aligned} \eta/s = 0.09 \pm 0.02 {} \end{aligned} $$

(7.50)

in agreement with former estimates of Teaney and Gavin [170]. This value is very small and, in fact, close to the universal lower bound of η∕s = 1∕4π recently derived field theoretically [171].

Elliptic flow measurements thus confirm that the quark-gluon matter produced as $\sqrt {s} \rightarrow 200$ GeV is to a good approximation in local thermal equilibrium up to about 3–4 fm/c. In addition, the final hadron mass dependence of the flow pattern is consistent with a universal scaling appropriate for a nearly non-viscous hydrodynamic flow of partons, and the observed v ₂ signal reflects a primordial equation of state that is consistent with first numerical QCD computations [153, 154, 165] of a strongly coupled quark-gluon plasma (sQGP) state. First estimates of its proper shear viscosity to entropy ratio, η∕s, are emerging from systematic analysis of the elliptic flow signal. At lower $\sqrt {s}$ precursor elliptic flow phenomena are observed, as well, but are more difficult to analyze as the crucial, new feature offered by top RHIC energies is missing here: a clear cut separation in time, between primordial formation of local partonic equilibrium conditions, and hadronization. At RHIC (and at future LHC) energy elliptic flow systematics thus captures the emerging quark-gluon state of QCD at energy densities in the vicinity of 𝜖 = 6–15 GeV/fm³, at temperature T ≈ 300 MeV, and μ _B → 0, describing it as a strongly coupled, low viscosity liquid medium.

7.5 In-medium Attenuation of High p _T Hadron and Jet Production

In the preceding sections we have followed the dynamical evolution of bulk matter in A+A collisions (at p _T ≤ 2 GeV which covers about 95% of the hadronic output), from initial formation time of partonic matter which reflects in charged particle transverse energy and multiplicity density, also giving birth to hadrons, and to the elliptic expansion flow signal.

An alternative approach toward QCD plasma diagnostics exploits the idea [41, 172] of implanting partonic products of primordial high Q ² processes into the evolving bulk medium, that could serve as “tracers” of the surrounding, co-traveling matter. The ideal situation, of being able to scatter well defined partons, or electrons, from a plasma fireball, is approximated by employing primordially formed charm-anticharm quark pairs [41], or leading partons from primordial di-jet production [172]. Both processes are firmly anchored in perturbative QCD and well studied in elementary collisions (where such partons are directly released into vacuum), which thus serve as a reference in an analysis that quantifies the in-medium modification of such tracer partons. Not a surprise, in view of our above inferences, from elliptic flow, of a high temperature, strongly coupled primordial medium: these in-medium modifications are quite dramatic, leading to a suppression of J∕ Ψ production from primordial $c \overline {c}$ pairs (Sect. 7.6), and to high p _T hadron and jet quenching, the subject of this chapter.

7.5.1 High p _T Inclusive Hadron Production Quenching

At top RHIC energy, $\sqrt {s}=200$ GeV, di-jet production from primordial hard pQCD parton-parton collisions (of partons from the initial baryonic structure functions) is the source of “leading” partons, with E _T up to about 30 GeV. They are derived from the inclusive cross section arising if the A+A collision is considered, first, as an incoherent superposition of independent nucleon-nucleon collisions, as enveloped within the target-projectile nucleon densities. In this framework, the pQCD cross section for producing an E _T parton in A+B takes the form of “factorization” [173]

$$\displaystyle \begin{aligned} \frac{{\mathrm{d}} \sigma}{{\mathrm{d}}E_{\mathrm{T}} \;{\mathrm{d}}y}= \sum_{a,b}\: \int_{x_a} {\mathrm{d}}x_a \int_{x_b} {\mathrm{d}}x_b \: f _{a/A} (x_a) f_{b/B} (x_b) \: \frac{{\mathrm{d}} \sigma_{ab}}{{\mathrm{d}} E_{\mathrm{T}} \;{\mathrm{d}}y} {} \end{aligned} $$

(7.51)

where the f(x) are the parton distributions inside projectile A and target B nuclei, and the last term is the pQCD hard scattering cross section. This equation describes the primordial production rate of hard partons, leading to the conclusion [172] that, at RHIC energy, all hadrons at p _T ≥ 6–10 GeV should arise from initial pQCD parton production.

As partons are effectively frozen during the hard scattering, one can treat each nucleus as a collection of free partons. Thus, with regard to high p _T production, the density of partons within the parton distribution function of an atomic number A nucleus should be equivalent to the superposition of A independent nucleons N:

$$\displaystyle \begin{aligned} f_{a/A} \: (x, Q^2)= A \: f_{a/N} \: (x, Q^2). {} \end{aligned} $$

(7.52)

From Eqs. (7.51) and (7.52) it is clear that the primordial high Q ² inclusive parton cross section in a minimum bias A+B reaction scales as A ⋅ B times the corresponding (N+N or) p+p cross section. Furthermore, as each leading parton ends up in an observed high p _T hadron h, we thus write the invariant hard hadron cross section as

$$\displaystyle \begin{aligned} E \;{\mathrm{d}} \sigma_{{\mathrm{AB}} \rightarrow h} / {\mathrm{d}}^3p = A \cdot B \cdot E \:\; {\mathrm{d}} \sigma_{pp \rightarrow h}/{\mathrm{d}}^3 p. {} \end{aligned} $$

(7.53)

Since nucleus-nucleus experiments usually measure invariant yields N _h for a given centrality bin, corresponding to an average impact parameter b, one writes instead:

$$\displaystyle \begin{aligned} E \;{\mathrm{d}} N_{\mathrm{AB} \rightarrow h} (b) / {\mathrm{d}}^3p = \left<T_{\mathrm{AB}} (b)\right>E \: {\mathrm{d}} \sigma_{pp \rightarrow h}/{\mathrm{d}}^3 p, {} \end{aligned} $$

(7.54)

where T _AB(b) is the Glauber geometrical overlap function of nuclei A, B at impact parameter b, which accounts for the average number of participant parton collisions at given impact geometry [174], $\left <N_{\mathrm {coll}}(b)\right >$. One can thus quantify the attenuating medium effects, as experienced by the primordially produced tracer parton on its way toward hadronization, by the so-called nuclear modification factor for hard collisions (analogous to Eq. (7.6), that refers to soft, bulk hadron production):

$$\displaystyle \begin{aligned} R_{\mathrm{AB}} (p_{\mathrm{T}}, y, b) = \frac{{\mathrm{d}}^2 N_{\mathrm{AB}}/{\mathrm{d}}y \;{\mathrm{d}}p_{\mathrm{T}}}{\left<T_{\mathrm{AB}}(b)\right>\: {\mathrm{d}}^2 \sigma_{pp}/{\mathrm{d}}y \; {\mathrm{d}}p_{\mathrm{T}}}. {} \end{aligned} $$

(7.55)

Obviously, this concept of assessing the in-medium modification of hadron production at high p _T requires corresponding p+p collision data, as a reference basis. Such data have been, in fact, gathered at top RHIC, and top SPS energies, $\sqrt {s}=200$ and 17.3 GeV, respectively. Alternatively, in situations where the relevant reference data are not known, one considers the production ratio of hadronic species h, observed in central relative to peripheral collisions:

$$\displaystyle \begin{aligned} R_{\mathrm{CP}}(p_{\mathrm{T}}, y)= \frac{{\mathrm{d}}^2 N_{\mathrm{h}}(b_1)/{\mathrm{d}}y \;{\mathrm{d}}p_{\mathrm{T}}}{{\mathrm{d}}^2 N_{\mathrm{h}} (b_2)/{\mathrm{d}}y \;{\mathrm{d}}p_{\mathrm{T}}} \: \times \: \frac{\left<T_{\mathrm{AB}}(b_2)\right>}{\left<T_{\mathrm{AB}}(b_1)\right>} {} \end{aligned} $$

(7.56)

where b ₁ ≪ b ₂ are the average impact parameters corresponding to the employed trigger criteria for “central” and “peripheral” A+A collisions, respectively. This ratio recasts, to a certain extent, the in-medium attenuation analysis, offered by R _AB, insofar as peripheral collisions approach the limiting conditions, of a few single nucleon-nucleon collisions occurring in the dilute surface sections of the nuclear density profiles, i.e. essentially in vacuum.

Employing the above analysis schemes, the RHIC experiments have, in fact, demonstrated a dramatic in-medium suppression of the high p _T yield, for virtually all hadronic species. Figure 7.41 shows R _AA for neutral pions produced in min. bias Cu+Cu and Au+Au collisions at $\sqrt {s}=200$ GeV where PHENIX extended the p _T range up to 18 GeV/c [175]; the nuclear modification factor refers to the range p _T > 7.0 GeV/c and is shown as a function of centrality, reflected by N _part. We infer a drastic suppression, by an R _AAapprox0.25 in near central collisions. Figure 7.42 shows the p _T dependence [175] of neutral pion R _AA in central Au+Au collisions (N _part = 350), with a suppression to below 0.2 at p _T ≥ 4 GeV/c.

Fig. 7.41

The nuclear modification factor R _AA for π ⁰ in min. bias Cu+Cu and Au+Au collisions at $\sqrt {s}=200$ GeV, in the range p _T > 7 GeV/c [175], plotted vs. centrality as measured by participant nucleon number N _part

Fig. 7.42

R _AA for π ⁰ production in central Au+Au collisions at $\sqrt {s}=200$ GeV [175], compared to a hydrodynamic calculation for different opacities (transport coefficients [195]) of the plasma [204]

Note that R _AAcannot reach arbitrarily small values because of the unattenuated contribution of quasi-in-vacuum surface “corona” single nucleon-nucleon collisions, closely resembling the p + p → π ⁰ + X inclusive yield employed in the denominator of R _AA, Eq. (7.55). Even in a central trigger configuration this suggests a lower bound, R _AA ≈ 0.15. Nuclear attenuation of high p _T pions thus appears to be almost “maximal”, implying a situation in which the interior sections of the high energy density fireball feature a very high opacity, i.e. they are almost “black” to the high p _T partons contained in pions.

We remark here, briefly, on a confusing feature that occurs in Fig. 7.42 (and in the majority of other R _AA vs. p _T plots emerging from the RHIC experiments): the pQCD number of collision scaling employed in R _AA does not describe pion production at low p _T as we have demonstrated in Sect. 7.2. The entries at p _T ≤ 3 GeV/c are thus besides the point, and so are pQCD guided model predictions, as shown here [176].

Nuclear modification analysis at RHIC covers, by now, the high p _T production of a multitude of mesonic and baryonic species [177], most remarkably even including the charmed D meson which is measured via electrons from semi-leptonic heavy flavor decay by PHENIX [175] and STAR [178]. Figure 7.43 illustrates the first PHENIX results from central Au+Au at $\sqrt {s}=200$ GeV, R _AA falling to about 0.3 at 5 GeV/c. Heavy flavor attenuation thus resembles that of light quarks, as is also attested by the predictions of in-medium parton transport models [179, 180] included in Fig. 7.43, which cast the medium opacity into an effective parton transport coefficient $\hat {q}$ which is seen here to approach a value 14 GeV²/c at high p _T, again corresponding to a highly opaque medium. We shall describe this approach in more detail below.

Fig. 7.43

The nuclear modification factor R _AA vs. p _T for electrons from semi-leptonic decays of heavy flavor (mostly D) mesons in central Au+Au collisions at $\sqrt {s}=200$ GeV [175]; with calculations of in medium energy loss using different attenuation models [179, 180]

A most fundamental cross-check of the in-medium attenuation picture of color charged partons consists in measuring R _AA for primordial, “direct” photons. Figure 7.44 shows first PHENIX results [181] for direct photon R _AA vs. p _T in central Au+Au at $\sqrt {s}=200$ GeV. Photons obey pQCD number of collisions scaling, R _AA ≈ 1! Also included in Fig. 7.44 are the attenuation ratios for neutral pions (already shown in Fig. 7.42), and for η mesons that follow the pattern of extreme suppression. In essence, the PHENIX results in Figs. 7.43 and 7.44 wrap up all one needs to know for a theoretical analysis of fireball medium opacity, for various flavors, and indicate transparency for photons.

Fig. 7.44

Modification factor R _AA vs. p _T for direct photons in central Au+Au at 200 GeV (squares). Also shown are R _AA for π ⁰ (triangles) and η (circles) [181] fitted by the attenuation model [176, 180]

We turn, briefly, to R _CP as opposed to R _AA analysis, in order to ascertain similar resulting conclusions at RHIC energy. Figure 7.45 illustrates an R _CP analysis of π, p and charged hadron high p _T production in Au+Au at $\sqrt {s}=200$ GeV by STAR [182], the central to peripheral yield ratio referring to a 5%, and a 60–80% cut of minimum bias data. We showed in Eq. (7.56) that the R _CP measure also refers to a picture of pQCD number of binary collision scaling, inappropriate at low p _T. Thus ignoring the features of Fig. 7.45 at p _T ≤ 3 GeV/c we conclude that the high p _T data again suggest a suppression by about 0.3, common to pions and protons, thus approaching the ratio, of about 0.2, observed in Figs. 7.41 and 7.42 which employ the “ideal” in-vacuum p + p → hadron + X reference.

Fig. 7.45

R _CP, the ratio of scaled π, p and charged hadron yields vs. p _T in central (5%) and peripheral (60–80%) Au+Au collisions at $\sqrt {s}=200$ GeV [182]

At top SPS energy, $\sqrt {s}=17.3$ GeV, the experimentally covered p _T range is fairly limited [183], p _T < 4 GeV/c. Figure 7.46 shows NA49 results, R _CP for p and charged pions. Contrary to former expectations that such data would be overwhelmed by Croonin-enhancement [184] the same systematic behavior as at RHIC is observed, qualitatively: R _CP (baryon)> R _CP (meson) at p _T > 3 GeV/c. Note that, again, the data do not approach unity at p _T → 0 because of the employed binary scaling, and that the strong rise of the proton signal at p _T < 2 GeV/c is largely the result of strong radial flow in central Pb+Pb collisions, an effect much less prominent in pion p _T spectra. The high p _T suppression is much weaker than at RHIC but it is strong enough that the expected Croonin enhancement of high p _T mesons is not observed. These SPS data, as well as first results obtained at the intermediate RHIC energy of $\sqrt {s}=62.4$ GeV [185] are reproduced by an attenuation model based on the primordial gluon density d N _g∕d y that scales as the charged particle midrapidity density d N _ch∕d y [176], and was also employed in Figs. 7.43 and 7.44.

Fig. 7.46

R _CP results from SPS Pb+Pb collisions at $\sqrt {s}=17.3$ GeV, for pions and protons [183], with attenuation model fits [176]

7.5.2 Energy Loss in a QCD Medium

The attenuation model that we have hinted at consists of a gluon radiative energy loss theory of the primordially produced leading, high p _T parton as it traverses a medium of color charges, by means of emission of gluon bremsstrahlung. We expect that the resulting partonic specific energy loss, per unit pathlength (i.e. its dE∕dx) should reflect characteristic properties of the traversed medium, most prominently the spatial density of color charges [176] but also the average momentum transfer, per in-medium collision of the considered parton or, more general, per unit pathlength at constant density. Most importantly, an aspect of non-abelian QCD leads to a characteristic difference from the corresponding QED situation: the radiated gluon is itself color-charged, and its emission probability is influenced, again, by its subsequent interaction in the medium [186] which, in turn, is proportional to medium color charge density and traversed pathlength L. Thus, the traversed path-length L in-medium occurs, both in the probability to emit a bremsstrahlung gluon, and in its subsequent rescattering trajectory, also of length L, until the gluon finally decoheres. Quantum mechanical coherence thus leads to the conclusion that non-abelian dE∕dx is not proportional to pathlength L (as in QED) but to L ² [187].

This phenomenon occurs at intermediate values of the radiated gluon energy, ω, in between the limits known as the Bethe-Heitler, and the factorization regimes [186],

$$\displaystyle \begin{aligned} \omega_{\text{BH}} \approx \lambda \: q^2_{\mathrm{T}} \ll \omega \ll \omega_{\text{fact}} \approx L^2 \: q_{\mathrm{T}}^2 /\lambda \le E {} \end{aligned} $$

(7.57)

where λ is the in-medium mean free path, $q_{\mathrm {T}}^2$ the (average) parton transverse momentum square, created per collision, and E the total cm energy of the traveling charge. In the BDMPSZ model [186,187,188] the properties of the medium are encoded in the transport coefficient, defined as the average induced transverse momentum squared per unit mean free path,

$$\displaystyle \begin{aligned} \hat{q} = \left<q^2_{\mathrm{T}}\right>/ \lambda. {} \end{aligned} $$

(7.58)

The scale of the radiated gluon energy distribution ω dN∕dω is set by the characteristic gluon energy [186, 187]

$$\displaystyle \begin{aligned} \omega_{\mathrm{c}}=\frac{1}{2} \: \hat{q} \: L^2. {} \end{aligned} $$

(7.59)

To see more explicitly how the various properties of the color charged medium enter in $\hat {q}$ we rewrite it as

$$\displaystyle \begin{aligned} \hat{q}= \rho \int q^2_{\mathrm{T}} \: {\mathrm{d}}q^2_{\mathrm{T}} \: \frac{{\mathrm{d}} \sigma}{{\mathrm{d}} q^2_{\mathrm{T}}} \equiv \rho \sigma \left<q^2_{\mathrm{T}}\right>= \lambda^{-1} \left<q^2_{\mathrm{T}}\right>{} \end{aligned} $$

(7.60)

where ρ is the color charge density of scattering centers, σ the effective binary cross section for interaction of the considered leading parton at scale q ² (which may depend on quark flavor), and $\left <q^2_{\mathrm {T}}\right >$ as above. Obviously, both σ and $\left <q^2_{\mathrm {T}}\right >$ refer to detailed, intrinsic properties of the QCD medium, globally described by density ρ. The leading parton cross section with in-medium color charges should depend on the implied resolution scale, $Q^2=\left <q^2_{\mathrm {T}}\right >$, and can thus be obtained from perturbative QCD [186,187,188] only if $Q^2 > Q^2_{\text{sat}}$, the saturation scale that we discussed in Sect. 7.2. Likewise, $\left <q^2_{\mathrm {T}}\right >$ itself reflects a medium property, the effective range of the color force, which is different in confined and deconfined media. Hadron size limits the force range in the former case, such that $\hat {q}$ is minimal in ground state hadronic matter also, of course, due to the small energy density ρ = ρ ₀ = 0.15 GeV/fm³ [189]. This was, in fact, confirmed by a RHIC run with deuteron-gold collisions, in which mid-rapidity hadrons traverse sections of cold Au nucleus spectator matter. Figure 7.47 shows results obtained for R _dA dependence on p _T, for π ⁰ from PHENIX [190], and for charged hadrons from STAR [191]. For comparison, both panels also include the corresponding R _AA data for central Au+Au collisions (all at $\sqrt {s}=200$ GeV/c), exhibiting the typical, drastic high p _T quenching of inclusive hadron production, clearly absent in d+Au collisions.

Fig. 7.47

R _AA vs. p _T for d+Au collisions at $\sqrt {s}=200$ GeV, compared to central Au+Au results, for π ⁰ (left) and charged hadrons (right). From [190, 191]

We have shown a first application of the BDMPSZ model, to RHIC inclusive D meson production [179], in Fig. 7.43. Before engaging in further model application we note, first, that Eqs. (7.57)–(7.60) above refer to the idealized conditions of an infinitely extended medium of uniform composition. In reality, the fireball medium expands, at time scale concurrent with the proper time incurred in the leading partons propagation over distance L, such that all ingredients in $\hat {q}$, exhibited in Eq. (7.60), vary with expansion time [192]. However, before turning to adaption to reality of the infinite matter model, we wish to expose its prediction for the final connection of the specific average partonic energy loss $\left <\Delta E\right >$ and in-medium path length L traversed:

$$\displaystyle \begin{aligned} \left<\Delta E\right> = \int \omega \frac{{\mathrm{d}} N}{{\mathrm{d}} \omega} \: {\mathrm{d}} \omega \propto \alpha_{\mathrm{s}} \: C_{\mathrm{R}} \: \hat{q} \: L^2. {} \end{aligned} $$

(7.61)

This relation [193] represents the eikonal approximation limit of extended medium and high leading parton initial energy E > ω _c (Eq. (7.59)). The average energy loss is thus proportional to the appropriate strong coupling constant α _s, to the Casimir factor corresponding to the leading parton (with value 4/3 for quarks, and 3 for gluons), as well as to $\hat {q}$ and L ².

In order to verify the non-abelian nature of radiative parton energy loss in a partonic QCD medium it would, of course, be most convincing if a direct, explicit L ² dependence of $\left <\Delta E\right >$ could be demonstrated. Such a demonstration is lacking thus far, chiefly because of the obvious difficulty of simultaneously knowing the primordial parton energy E, the transport coefficient $\hat {q}$ and—in finite nuclear collision geometry—its variation along the actual traversed path L as the surrounding medium expands with propagation time. Moreover, the partonic medium induced energy loss ΔE of the primordial parton is not directly observable. Even if we assume that high p _T partons evolve into the observed hadrons only after leaving the fireball medium [176], their ensuing “fragmentation” to hadrons (which is known from p + p jet physics) results in several hadrons usually comprising a “leading” hadron which transports a major fraction $\left <z\right >\equiv \left <E^{\mathrm {h}}/E^{\mathrm {p}}\right >$ of the fragmenting parton energy E ^p, which, in turn, equals E ^p (primordial)—ΔE, with ΔE sampled from a probability distribution with mean $\left <\Delta E\right >$ according to Eq. (7.61). The observed leading hadron energy or transverse momentum is thus subject to sampling, both, z from the fragmentation function, and ΔE from in-medium energy loss. Finally, inclusive high p _T leading hadron observation in A+A collisions involves an average over all potential initial parton production points, within the primordially produced density profile. A specific distribution of in medium path lengths f(L) arises, for each such production point, which, moreover, depends on a model of space-time fireball expansion. The final inclusive yield thus requires a further, weighted volume average over f(L) per production point. Thus, typical of an inclusive mode of observation, the “ideal” relationship of Eq. (7.61), between radiative in-medium energy loss ΔE and traversed path length L gets shrouded by double averages, independently occurring at either side of the equation [176, 179, 189, 194,195,196]. A detailed L ² law verification cannot be expected from inclusive central collision data alone (see next section).

However, the unmistakably clear signal of a strong, in-medium high p _T parton quenching effect, gathered at RHIC by R _AA measurement for a multitude of hadronic species (Figs. 7.20, 7.41, 7.42, 7.43, 7.45, and 7.47), in Au+Au collisions at $\sqrt {s}=200$ GeV, has resulted in first estimates of the transport coefficient $\hat {q}$, the medium—specific quantity entering Eq. (7.61), in addition to the geometry—specific path length L. In fact, the transport coefficient can, to some extent, be analyzed independently, owing to the fact that $\hat {q} \propto \varrho$ from Eq. (7.60). The density ϱ falls down rapidly during expansion, but it is initially rather well constrained by the conditions of one-dimensional Bjorken expansion that we have described in Sects. 7.2 and 7.4. The major contribution to partonic ΔEarises in the early expansion phase (via a high $\hat {q}$), in close analogy to the formation of the elliptic flow signal. These two signals are, thus, closely correlated: the primordial hydrodynamic expansion phase of bulk matter evolution sets the stage for the attenuation, during this stage of QCD matter, of primordially produced “tracer” partons, traversing the bulk matter medium as test particles.

The bias in partonic ΔE to the primordial expansion period is borne out in an expression [193, 195] which replaces the $\hat {q}$ coefficient, appropriate to an infinitely extended static medium considered in the original BDMPSZ model, by an effective, expansion time averaged

$$\displaystyle \begin{aligned} \hat{q}_{\text{eff}} = \frac{2}{L^2} \int^L_{t_0} \: {\mathrm{d}}t \:(t-t_0)\: \hat{q} \: (t) {}\end{aligned} $$

(7.62)

to be employed in the realistic case of an expanding fireball source. Due to the rapid fall-off of ϱ, in $\hat {q}=\varrho \sigma \:\left <q_{\mathrm {T}}^2\right >$ from Eq. (7.60), the integral depends, far more strongly, on $\hat {q} \: (t \approx t_0)$ than on total path length L. Furthermore, inserting $\hat {q}_{\text{eff}}$ into the BDMPSZ formula [193, 195] for the transverse momentum downward shift, occurring in leading parton or hadron p _T spectra (of power law form $p_{\mathrm {T}}^{-\nu }$, see Fig. 7.20)

$$\displaystyle \begin{aligned} \Delta \: p_{\mathrm{T}} \approx - \alpha_{\mathrm{s}} \sqrt{\pi \hat{q} L^2 p_{\mathrm{T}}/\nu}, {}\end{aligned} $$

(7.63)

we see that the first order proportionality to L ² is removed. The downward p _T shift is thus, primarily, a consequence of $\hat {q}_{\text{eff}}$ which, in turn, is biased to reflect the “ideal” transport coefficient $\hat {q}$ at early evolution time. Within this terminology, the p _T shift (see Eq. (7.63)) determines the experimentally measured ratio R _AA(p _T) which quantifies the effective transport coefficient $\hat {q}_{\text{eff}}$ for the p _T domain considered. It can be related, as a cross check, to the initial gluon rapidity density if the collision region expands according to Bjorken scaling [187, 197]:

$$\displaystyle \begin{aligned} \hat{q} = \alpha_{\mathrm{s}} \: \frac{2}{L} R^{-2}_A \: \frac{{\mathrm{d}} N^g}{{\mathrm{d}} y}. {}\end{aligned} $$

(7.64)

A typical result of application of the model described above [195] is shown in Fig. 7.48. Analogous to Fig. 7.41, R _AA for neutral pions and charged hadrons is averaged over the range 4.5 ≤ p _T ≤ 10 GeV/c, and shown as a function of centrality (assessed by N _part) in minimum bias Au+Au collision at $\sqrt {s}= 200$ GeV [190, 191, 198]. A path-averaged $\hat {q}_{\text{eff}}$ of 14 GeV²/fm is inferred from the fit, in close agreement to the value found in [195].

Fig. 7.48

The effective transport coefficient $\hat {q}=14$ GeV²/fm in the parton quenching model (PQM) of [195] determined from the centrality dependence of R _AA for π ⁰ and charged hadrons, averaged over 4.5 ≤ p _T ≤ 10 GeV/c, in Au+Au at $\sqrt {s}=200$ GeV

A more recent study [199] of the PHENIX R _AA data for π ⁰ in central Au+Au collisions (Fig. 7.42) is shown in Fig. 7.49. The analysis is carried out in the framework of the WHDG model [200], which replaces the (effective) transport coefficient $\hat {q}$ (employed in the BDMPSZ model [186,187,188], and turned into the data analysis formalism of [193, 195]) by the primordial gluon mid-rapidity density dN ^g∕dy, as the fundamental parameter, via Eq. (7.64). The initial gluon density, in turn, being related to the charged hadron mid-rapidity density [61]. Figure 7.49 shows that, within the still preliminary statistics at p _T > 10 GeV/c, the “conservative” estimate of α _s = 0.3 and dN ^g∕dy = 1000 does not appear to be the most appropriate choice, the data rather requiring 1000 < dN ^g∕dy < 2000. Overall, Fig. 7.49 demonstrates a certain insensitivity of the data, to the basic parameters of theoretical high p _T quenching models of inclusive hadron production at RHIC energy, that we have already inferred from Fig. 7.43, concerning choice of $\hat {q}$.

Fig. 7.49

Application of the WDHG transport model [200] based on Eq. (7.64) to PHENIX R _AA data for π ⁰ [175], indicating primordial 1000 ≤ (d N ^g)∕(d y) ≤ 2000

Radiative in-medium energy loss of primordially produced partons, traversing the evolving bulk medium as “tracers”, must be extremely strong. This is indicated by the inclusive attenuation ratios R _AA, which fall down to about 0.2 in central collisions thus almost reaching the absolute lower limit of about 0.15 that arises from the unavoidable fraction of un-attenuated primordial surface “corona” nucleon-nucleon interaction products [201].

Not expected from early estimates of medium opacity based on the picture of a weakly coupled perturbative QCD medium [172, 202], the interior sections of the central Au+Au interaction volume must be almost “black” toward high p _T parton transport [194, 195] at $\sqrt {s}=200$ GeV, also including charm quark propagation (Fig. 7.43). The remaining signal should thus stem, primarily, from the dilute surface sections, and from the finite fraction of partons traversing the interior with small, or zero radiative energy loss, as a consequence of the finite width of the ΔE probability distribution [193, 194]. Seen in this light, the smooth decrease of R _AA with centrality (Fig. 7.48) should reflect the combined effects, of a decreasing surface to volume ratio, an increasing effective $\hat {q}$ (due to interior density increase) that confronts the increasing average geometrical potential path length $\left <L\right >$ (essentially enhancing its effect), and a thus diminishing fraction of primordial high p _T partons experiencing a small ΔE.

Not surprisingly, the ideal non abelian QCD relationship of ΔE proportional to in-medium high p _T parton path length L ² can, thus, not be established from inclusive high p _T quenching data alone. We shall show in the next section that di-jet primordial production can offer a mechanism of higher resolution. The inclusive R _AA attenuation data, obtained at RHIC, are seen to establish an unexpected, high opacity of the primordial interaction volume, extending to high p _T parton propagation. The required, high transport coefficient $\hat {q} = 14$ GeV²/fm from Fig. 7.48, confirms and extends the picture derived from elliptic flow data [167]: at top RHIC energy the plasma is non-perturbatively, strongly coupled, a new challenge to lattice QCD [61]. The QGP may be largely composed of colored, string-like partonic aggregates [203].

7.5.3 Di-jet Production and Attenuation in A+A Collisions

In order to analyze leading parton attenuation in a more constrained situation [204], one investigates parton tracer attenuation under further geometrical constraints concerning the in-medium path length L, by means of di-jet analysis, and/or by varying the primordial parton density that enters $\hat {q}$ via Eq. (7.60) in studies at different $\sqrt {s}$ while maintaining the observational geometrical constraints.

We shall concentrate here on di-jet attenuation data obtained in Au+Au collisions at top RHIC energy, $\sqrt {s}=200$ GeV. At this relatively modest energy the initial pQCD production cross section of leading partons (as described in Eq. (7.51)) reaches up to p _T = 25 GeV/c. The ensuing DGLAP shower multiplication initiates “parton fragmentation” to hadrons [83, 85, 121], each carrying a momentum fraction z _T = p _T∕p _T (primord. parton). The created ensemble of hadrons h belonging to the observed hadronic jet can be wrapped up by the total fragmentation function

$$\displaystyle \begin{aligned} F_{\mathrm{h}} \: (z, \sqrt{s}) = \sum_i \int \frac{{\mathrm{d}}z}{z} C_i \: (z, \sqrt{s}) \; D_{\text{part} \rightarrow h} (z, \sqrt{s}) {} \end{aligned} $$

(7.65)

which summarizes the contributions arising from the different shower partons i. Here, C _i are the weight coefficients of the particular process, and D _part(i)→h are the individual fragmentation functions (FFs) for turning parton i into hadron h. Similar to the parton distribution functions (PDFs) in Eq. (7.51), derived from deep inelastic electron-parton scattering (DIS) and shown in Fig. 7.14, the FFs are semi-empirical non-perturbative QCD functions that have an intuitive probabilistic interpretation. They quantify the probability that the primordial parton produced at short distance 1∕Q fragments into i shower partons, forming a jet that includes the hadron h [205, 206].

At Fermilab energy, $\sqrt {s}=1.8$ TeV, the jet spectrum reaches up to E _T ≈ 400 GeV, and a typical 100 GeV jet comprises about 10 hadrons which can be identified above background by jet-cone reconstruction algorithms [205]. This allows for a complete determination of the corresponding fragmentation function, and for a rather accurate reconstruction of the p _T and E _T of the primordial parton that initiated the jet. Similar conditions will prevail in jet spectroscopy of Pb+Pb collisions at LHC energy, $\sqrt {s}=5.5$ TeV.

However, at RHIC energy a typical jet at 15 ≤ E _T ≤ 25 GeV features a fragmentation function comprised of a few hadrons with E _T in the 2–15 GeV range. Considering the high background, arising in the lower fraction of this energy domain from concurrent, unrelated high p _T hadron production processes, a complete jet-cone analysis cannot succeed. The RHIC experiments thus confront back-to-back di-jet production with an analysis of the azimuthal correlation between high p _T hadrons. Defining the observational geometry by selecting a high p _T “trigger” hadron observed at azimuthal emission angle φ _trig, the associated production of high p _T hadrons is inspected as a function of Δφ = φ _ass − φ _trig. If the trigger has caught a leading jet hadron one expects the hadrons of the balancing back-to-back jet to occur at the side opposite to the trigger, Δφ ≈ π. The trigger condition thus imposes the definition of a “near-side” and an “away side” azimuthal domain. Furthermore, the relatively narrow rapidity acceptance of the STAR and PHENIX experiments (centered at y = 0) selects di-jets with axis perpendicular to the beam direction.

Originating from a uniform distribution of primordial back-to-back di-parton production vertices, throughout the primordial reaction volume, the trigger selected di-jet partons thus experience an (anti-)correlated average path length $\left <L\right >$ to arrive at the surface while experiencing medium-specific attenuation, with $\left <L_{\text{trig}}\right >\approx 2 R - \left <L_{\text{away}}\right >$, R being the transverse medium radius. No such geometric constraint exists in the study of inclusive high p _T hadron production. We thus expect information different from the inclusive R _AA(p _T) signal. The geometrical selectivity can be even further constrained by fixing the direction of the impact parameter (i.e. the reaction plane) in semi-central collisions (recall Sect. 7.4), and observing the di-jet correlation signal in dependence of the di-jet axis orientation relative to the reaction plane.

The very first di-hadron correlation measurements confirmed the existence of strong in-medium attenuation. Figure 7.50 shows the azimuthal yield distributions, per trigger hadron, as observed by STAR at $\sqrt {s}= 200$ GeV [207]. The left panel shows the distribution of hadrons with p _T ≥ 2 GeV/c relative to a trigger hadron with $p_{\mathrm {T}}^{\text{trig}} \ge 4$ GeV/c. Data for p+p, d+Au and central Au+Au are illustrated. At the “near side” (the trigger position is Φ = 0) all three reactions exhibit a similar narrow distribution of hadrons associated with the trigger hadron, typical of a jet cone fragmentation mechanism. Note that the associated near-side central Au+Au signal thus exhibits no signs of an attenuation softened fragmentation function, indicating that the trigger imposed high p _T hadron should predominantly stem from primordial jet production vertex points located near to the surface of the reaction volume, in azimuthal trigger direction. Thus, conversely, the balancing opposite jet has to develop while traversing almost the entire transverse diameter of the interaction volume. I.e. $\left <L_{\text{oppos}}\right >\approx 2 \: R$ thus emphasizing the expectation that di-jet spectroscopy should allow for stricter constraints on path length L in comparison to single high p _T hadron R _AA analysis. In fact, no trigger related away side signal of p _T > 2 GeV/c hadrons is observed in Fig. 7.50 for central Au+Au collisions, whereas p+p and central d+Au collisions exhibit a clear away-side di-jet signal.

Fig. 7.50

Di-hadron correlation from back-to-back di-jet production in Au+Au collisions at $\sqrt {s}=200$ GeV. The trigger particle is at azimuth Φ = 0, with a p _T > 4 GeV threshold. The away side peak at Δ Φ = π is observed (left panel) in p+p, d+A but absent in central Au+Au. Right panel shows the correlation in Au+Au for different orientations of the trigger direction relative to the reaction plane [207]

We conclude that the trigger bias, selecting a single near side hadron of p _T ≥ 4 GeV/c in central Au+Au collisions, responds to a primordial di-jet of about 10 GeV per back-to-back parton. After traversal of in medium average path length L → 2 R the fragmentation function of the opposite side parton contains on average no hadron at p _T > 2 GeV/c, indicating that it should have lost a fraction $\left <\Delta E_{\mathrm {T}}\right > \ge 5$ GeV. The medium is thus highly opaque, but the total disappearance of the opposite side signal can only provide for a lower limit estimate of $\left <\Delta E_{\mathrm {T}}\right >$, within the trigger conditions employed here. We shall show below that the situation changes with more recent RHIC data [208] that extend the trigger hadron p _T range toward 20 GeV/c.

However, the right hand panel of Fig. 7.50 shows that an improved constraint on partonic in-medium path length can already be obtained by studying the di-jet back-to-back production geometry in correlation with the orientation of the reaction plane that arises from non-zero impact parameter in semi-central A+A collisions. We have seen in Fig. 7.34 that such collisions exhibit an elliptical primordial transverse density profile, with minor axis along the impact vector $\vec {b}$, defining the reaction plane. Di-jets with axis “in-plane” thus traverse a shorter in-medium path length as orthogonal “out-of-plane” jets, the difference in average path length being quantified by the spatial excentricity 𝜖(b), Eq. (7.47). Figure 7.50 (right) shows the di-hadron correlation results in semi-peripheral Au+Au collisions, as compared to the in-vacuum p+p reference. At the 20–60% centrality window employed here, out of plane jet emission occurs along the major axis, the reaction volume diameter still of magnitude 2R, as in central collisions. The trigger condition thus again selects opposite side path lengths L → 2 R, but the energy density should be lower than in central collisions. Even so, the average opacity along the away side parton path appears to be high enough to wipe out the correlation signal. In-plane geometry, however, shows a partially attenuated signal (as compared to the global p+p reference) at the opposite side, corresponding to path lengths L ≈ R. These data thus provide for first information concerning the relation of $\left <\Delta E\right >$ and average traversed path length [176].

Obviously, one wants to extend the above study to higher di-jet energies, i.e. to measurement of di-hadron correlations at hadron trigger p _T → 20 GeV/c, conditions sampling the very low primordial cross section, at $\sqrt {s}=200$ GeV, of jet production at primordial E _T → 30 GeV [208, 209]. Figure 7.51 shows the corresponding jet correlations selected with high p _T trigger, $8 < p_{\mathrm {T}}^{\text{trig}} < 15$ GeV/c, and high p _T associated hadrons, p _T > 6 GeV/c, in minimum bias d+Au, semi-central Au+Au and central Au+Au at $\sqrt {s}=200$ GeV. Very clear and almost background-free back-to-back jets are observed in all three cases, in sharp contrast with the away side jet total disappearance in central Au+Au at lower jet energy, Fig. 7.50 (left panel). The near side trigger associated hadron yield decreases only slightly from d+A to central Au+Au, while the away side yield drops down by an attenuation factor of about 0.2, the signal thus not being completely extinguished. We infer R _AA(L → 2R) ≈ 0.2.

Fig. 7.51

Di-hadron correlation at high p _T in central Au+Au collisions at $\sqrt {s}=200$ GeV, compared to d+Au and peripheral Au+Au; for $8 \le p_{\mathrm {T}}^{\text{trig}} \le 15$ GeV, and $p_{\mathrm {T}}^{\text{assoc}} > 6$ GeV. From [208]

In order to show how such data can be evaluated in a picture of in-medium leading parton attenuation (as finally reflected in leading hadron production observed in the above di-hadron correlation data) we briefly consult the pQCD factorization [210] prediction for the inclusive production of a high p _T hadron at central rapidity, in the nuclear collision A + B → h + x [196],

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{{\mathrm{d}}^3 \sigma_{\mathrm{AB} \rightarrow hx}}{{\mathrm{d}}^2 p_{\mathrm{T}} \; {\mathrm{d}} y} &\displaystyle =&\displaystyle K_{\text{NLO}} \sum_{abc} \int {\mathrm{d}} \vec{r} \; {\mathrm{d}}x_a \; {\mathrm{d}}x_b \; {\mathrm{d}}z_c \: F_{a/A} (x_a, Q^2, \vec{r}) \\ &\displaystyle &\displaystyle \times F_{b/B} (x_b, Q^2, \vec{b} - \vec{r}) \frac{{\mathrm{d}}^3 \sigma_ {ab-c}}{{\mathrm{d}}^2 p_{T (c)} \; {\mathrm{d}} y_c} (x_a,x_b, Q^2)\\ &\displaystyle &\displaystyle \times \frac{1}{z^2_c} \: D_{h/c} (z_c, Q^2) {} \end{array} \end{aligned} $$

(7.66)

where the parton (a, b) distribution functions F in nucleus A, B and the elementary pQCD cross section for a + b → c + x have been already implied in Eq. (7.51). Their spatial integral gets convoluted with the fragmentation function D that describes the conversion of the leading parton c to a hadron carrying a fraction 0 < z _c < 1 of its transverse momentum. K is a factor introduced as a phenomenological correction for “next to leading order” (NLO) QCD effects. Within the (further) approximation that the leading parton c suffers medium induced gluon bremsstrahlung energy loss but hadronizes outside the interaction volume (in vacuum), the in-medium quenching leads, merely, to a re-scaling of the fragmentation function,

$$\displaystyle \begin{aligned} D_{h/c}^{\text{med}} \: =\: \int {\mathrm{d}} \epsilon \: P (\epsilon) \frac{1}{1-\epsilon} \: D^{\text{vac}}_{h/c} \: \left(\frac{z_c}{1- \epsilon}, Q^2\right), {} \end{aligned} $$

(7.67)

where the primary parton is implied to lose an energy fraction 𝜖 =  ΔE∕E _c with probability P(𝜖) [196]. Therefore the leading hadron is a fragment of a parton with reduced energy (1 − 𝜖)E _c, and accordingly must carry a larger fraction of the parton energy, z _c∕(1 − 𝜖). If no final state quenching is considered, P(𝜖) reduces to δ(𝜖). The entire effect of medium attenuation on the leading parton is thus contained in the shift of the fragmentation function.

An application of this formalism [196] is shown in Fig. 7.52. The in-medium modification of the hadron-triggered fragmentation function (see Eq. (7.67)) is evaluated for central Au+Au collisions at $\sqrt {s}=200$ GeV. In adaptation to the modalities of RHIC di-hadron correlation data, the opposite side fragmentation function (for observation of trigger-related hadrons with p _T > 2 GeV/c) is studied in dependence of the trigger selected p _T window. Its attenuation is quantified by the ratio D (with quenching) to D (without quenching), as a function of the fraction z _T, of opposite side hadron p _T to trigger hadron p _T. Referring to the observational conditions implied in Fig. 7.50 (left) $p_{\mathrm {T}}^{\text{trig}} \approx 4$–6 GeV/c and opposite side p _T > 2 GeV, the predicted suppression amounts to a factor of about 0.35, whereas the data imply a factor smaller than 0.2. Likewise, comparing to the data of Fig. 7.51, the (harder) trigger conditions should lead to a suppression of about 0.45 from Fig. 7.52 but the observed value is close to 0.2. The predictions appear to fall short of the actually observed suppression. This calculation employs an ansatz for the transport coefficient $\hat {q}$ similar to Eq. (7.64), recurring to the primordial gluon density at τ ₀ ≤ 0.6 fm/c which, in turn, is estimated by the charged hadron mid-rapidity density [197]. However, this pQCD based argument can also not reproduce the magnitude of the effective transport coefficient (Eq. (7.62)), $\hat {q}_{\text{eff}} \approx 10$–15 GeV²/fm, shown in refs. [194, 195, 199] to be required by the large observed suppression (see Fig. 7.43).

Fig. 7.52

The ratio of the hadron-triggered fragmentation function, Eq. (7.67), in central Au+Au and in p+p collisions, for different values of $p_{\mathrm {T}}^{\text{trig}}$ [196]

It has been argued [199, 211] that these models need refinement by introducing more realistic dynamics, and/or by completely abandoning the pQCD ansatz for hard parton in-medium transport [212, 213]. We shall return to these novel suggestions, of how to treat dynamical, non equilibrium quantities of the “strongly coupled” parton plasma of non perturbative QCD (toward which equilibrium lattice theory can only give hints), in our final conclusion (Sect. 7.8). In the meanwhile, we note that the expected non abelian behavior, ΔE ∝ L ², could not be verified quantitatively, as of yet [211], because of the unexpectedly high opacity of the fireball interior sections at $\sqrt {s}=200$ GeV, in combination with the limited jet energy range that is available at RHIC energy. It appears possible, however, to extend the analysis of the “back side jet re-appearance” data [208, 209] (Fig. 7.51) toward this goal. The situation should improve at LHC energy, $\sqrt {s}=5.5$ TeV, where primordial 100–200 GeV jets are abundant, such that the opposite side jet can be reconstructed with explicit use of the complete Fermilab jet cone recognition algorithms [205] even if their in-medium E _T loss ranges up to 50 GeV.

A further prediction of the model employed in Fig. 7.52 has been confirmed by the RHIC experiments. The high medium opacity at top RHIC energy leads to an intriguing emission pattern of low p _T opposite side hadrons. Clearly, the trigger-selected E _T flux, of up to 20 GeV, toward the away-side, cannot remain unnoticeable. Inspection of the attenuated fragmentation functions [196] in Fig. 7.52 reveals an enhanced emission of bremsstrahlung gluon hadronization products at z _T ≤ 0.1 This fraction of in-medium jet-degradation products has in fact been observed, as is shown in Fig. 7.53. The left panel shows STAR results [214] for the di-hadron correlation in central Au+Au at $\sqrt {s}=200$ GeV, with near-side hadron trigger 4 < p _T < 6 GeV/c, and opposite side observation extended to soft hadrons, 0.15 < p _T < 4 GeV/c. A prominent double-peak structure is indicated, symmetric about Δ Φ = π. The right panel shows high resolution PHENIX results [215] for Au+Au at three centralities, from peripheral to central collisions. For the former, the typical p+p-like away side peak (c.f. Fig. 7.47) is recovered, while a double peak appears in the latter case, shifted from Δ Φ = π by ± δ Φ ≈ 70⁰. A hypothetical mechanism comes to mind [213], of sideward matter acceleration in a “Mach-cone” directed mechanism of compressional shock waves initiated by the in-medium energy loss of the opposite side leading jet parton, which traverses the medium at “super-sonic” velocity, i.e. at v > v _s, the appropriate speed of sound in a parton plasma.

Fig. 7.53

Di-hadron correlation: away side emission pattern in central Au+Au collisions, compared to pp data by STAR [214] (left panel) and to peripheral Au+Au (right panel) by PHENIX [215]

If confirmed by pending studies of the away-side multi-hadron correlation, that might ascertain the implied conical shape of the soft hadron emission pattern (about the direction Δ Φ ≈ π of the leading parton), this mechanism might lead to the determination of the sound (or shock wave) velocity of a strongly coupled parton plasma: a third characteristic QGP matter property, in addition to viscosity η (from elliptic flow) and $\hat {q}$ (from high p _T parton attenuation). We note that the implied concept, of measuring the shock wave transport velocity of a strongly interacting medium, dates back to the 1959 idea of Glassgold et al. [216], to study shock wave emission in central p+A collisions at AGS and PS proton energy, of about 30 GeV. In hindsight we can understand the inconclusiveness of such searches: the “low energy” incident proton does not preserve its identity, breaking up into relatively soft partons in the course of traversing the target nucleus. Their coupling to the surrounding cold baryonic target matter is weak, and possible collective transverse compressional waves are swiftly dissipated by the cold, highly viscous [61] hadronic medium. The shock compression and Mach-cone emission mechanism was then revived by Greiner et al. [217] for central ²⁰Ne + U collisions at Bevalac energy [218]. The recent RHIC observations in Fig. 7.53 have been called “conical flow” [219]; they demonstrate, again, the strong coupling to the medium, of even a 20 GeV/c leading parton [220].

7.6 Vector Meson and Direct Photon Production: Penetrating Probes

This chapter is devoted to three observables that have been profoundly studied already at the SPS, as tracers of the created fireball medium:

• 1. J∕ Ψ “charmonium” production, as suppressed in a high T QGP medium,

• 2. “direct” photons as black body T sensors of the QGP state;

• 3. ρ meson in medium production, studied by di-lepton decay.

These three observables represent an internally connected set of ideas of high density QCD matter diagnostics: all serve as medium tracers but in a complementary way. Matsui and Satz [41] realized that at the modest top SPS energy, $17.3 < \sqrt {s} < 20$ GeV, the production rate of $c \overline {c}$ pairs (that would in part develop toward charmonium production, J∕ Ψ, Ψ^′, etc.) was so low that only the primordial, first generation nucleon-nucleon collisions in an A+A event would create a measurable yield (nothing after thermalization). I.e. the primordial $c \overline {c}$ yield would be well-estimated by $A^{4/3} \ \sigma _{pp} (c \overline {c})$. Initially produced in a superposition of states including color triplets and octets [221] the emerging $c \overline {c}$ pairs thus co-travel with the developing high energy density fireball medium, as tracers, on their way toward J∕ Ψ or Ψ^′ and D, $\bar {\mathrm {D}}$ formation. Attenuation, characteristic of medium properties, will break up leading $c \overline {c}$ pairs resulting in a suppression of the eventually observed J∕ Ψ yield: another “quenching” observable.

As the suppression of J∕ψ is related to medium temperature and density, the extent of charmonium quenching should also be related to the rate of black body thermal fireball radiation, by photon emission via elementary $q \overline {q} \rightarrow g \gamma$ and qg → qγ processes in the plasma [222, 223]. Photons leave the interaction volume essentially un-rescattered, and their radiative intensity, proportional to T ⁴, makes them an ideal probe of the initial fireball temperature. This thus could be an ideal diagnostics of the early deconfined matter, but it is difficult to disentangle from a multitude of concurrent low p _T photon sources [224], most prominently π ⁰ → 2γ decay, with cross sections higher by several orders of magnitude. The thermal photon signal thus becomes more promising the higher the initial temperature T _i which might reach up to 500–600 MeV at LHC energy.

Similar to photons, in medium created lepton pairs [225] escape essentially un-attenuated as was shown for the Drell-Yan process, $q \overline {q} \rightarrow L \overline {L}$ by CERN experiment NA38/NA50 [226]. Thermal di-lepton production in the mass region ≤ 1 GeV is largely mediated by light vector mesons. Among these, the ρ meson is of particular interest due to its short lifetime (1.3 fm/c), making it an ideal tracer (via its in-medium di-lepton decay) for the modification of hadrons composed of light quarks, in the vicinity of T = T _c. This modification signal is thus complementary to the heavy quark charmonium J∕ Ψ suppression (break up) effect that sets in at T ≥ 1.5–2T _c (see below). Moreover, in addition to the deconfinement breakup mechanism by QCD plasma Debye screening of the color force potential acting on the $c \overline {c}$ pair [41], the QCD chiral symmetry restoration mechanism [227] can be studied via in-medium modification of the ρ spectral function as T → T _c. Note that the in vacuum ρ mass and width properties are owed to non-perturbative QCD condensate structures [1, 228] which spontaneously break the chiral symmetry of the QCD Lagrangian, at T → 0. These properties should change, in the vicinity of T _c, and be reflected in modifications of the di-electron or di-myon decay spectra—unlike the suppression effect on the J∕ Ψ which simply dissolves primordial $c \overline {c}$ pairs before they can hadronize, a yes-no-effect whose onset with $\sqrt {s}$ or centrality serves as a plasma thermometer, by observing R _AA or R _CP < 1.

7.6.1 Charmonium Suppression

Due to the high charm and bottom quark masses, the “quarkonium” states of $c \overline {c}$ and $b \overline {b}$ can be described in non-relativistic potential theory [229, 230], using

$$\displaystyle \begin{aligned} V(r) = \sigma r - \frac{\alpha}{r} {} \end{aligned} $$

(7.68)

as the confining potential [231], with string tension σ = 0.2 GeV² and gauge coupling α = π∕12. We are interested in the states J∕ Ψ (3.097), χ _c (3.53) and Ψ^′ (3.685) which are the 1S, 1P and 2S levels. The decay of the latter two feeds into the J∕ Ψ, accounting for about 40% of its yield. The radii derived from Eq. (7.68) are 0.25, 0.36 and 0.45 fm, respectively, well below hadron size at least for the J∕ Ψ and χ _c states.

With increasing temperature, σ(T) decreases, and at deconfinement σ(T _c) = 0. For T ≥ T _c we thus expect

$$\displaystyle \begin{aligned} V(r) = - \frac{\alpha}{r} \: \exp \: [-r/r_{\mathrm{D}} \: (T)] {} \end{aligned} $$

(7.69)

where r _D(T) is the QCD Debye screening radius. It was initially estimated from a SU (2) gauge theory of thermal gluons [41], to amount to about 0.2–0.3 fm at T∕T _c = 1.5. In this picture, the screened potential (Eq. (7.69)) can still give rise to bound $c \overline {c}$ states provided their radius is smaller than r _D. The pioneering study of Matsui and Satz [41] concluded that screening in a QGP system would dissolve the J∕ Ψ, or its $c\bar {c}$ precursor, at T ≥ 1.3 T _c whereas the χ _c and Ψ^′ states would be suppressed already directly above T _c.

The corresponding energy density for J∕ Ψ suppression, employing

$$\displaystyle \begin{aligned} \epsilon/\epsilon_{\mathrm{c}} \approx (T/T_{\mathrm{c}})^4 \approx 2.9 {} \end{aligned} $$

(7.70)

(obtained with 𝜖 _c ≈ 1 GeV/fm³ from lattice QCD), would thus amount to about 2.9 GeV/fm³. This motivated an extensive experimental effort at the CERN SPS Pb beam at $\sqrt {s}=17.3$ GeV. We have seen in Sect. 7.2 that the Bjorken estimate [45] of average transverse energy density reached in central Pb+Pb collisions [43, 44] amounts to 𝜖 = (3.0 ± 0.6) GeV/fm³, with higher 𝜖 to be expected in the interior fireball sections: encouraging conditions.

However, the above approach assumes the validity of a two-body potential treatment at finiteT, near a conjectured critical point of QCD. More recently the quarkonium spectrum was calculated directly in finite temperature lattice QCD [232], with the striking result that the J∕ Ψ dissociation temperature in a realistic non-perturbative treatment of the QCD plasma state moves up to about T = 2 T _c, whereas χ _c and Ψ^′ dissociation is expected [230] to occur at T = (1.1–1.2)T _c.

In addition to high T breakup of $c\bar {c}$ or J∕ Ψ, we have to take account of the so-called “normal suppression” of charmonium yields, observed in proton-nucleus collisions [233]. This effect is due to a re-scattering dissociation of the primordially produced, pre-hadronic $c \overline {c}$ system upon traversal of (cold) hadronic matter [234]. It can be studied in p+A collisions where the data on J∕ Ψ production relative to pp collisions can be described by the survival probability

$$\displaystyle \begin{aligned} S_{pA} \equiv \frac{\sigma_{pA}}{A \sigma_{pp}} = \int {\mathrm{d}}^2 b \int {\mathrm{d}}z \; \rho_A (b,z) \exp \left\{-(A-1) \int^{\infty}_z {\mathrm{d}}z^{\prime } \; \rho_A (b,z^{\prime }) \sigma_{\text{abs}}\right\} {} \end{aligned} $$

(7.71)

where σ _abs is the effective cross section for the “absorption” (break-up) of the $c \overline {c}$ in cold nuclear matter, and ρ _A is the transverse nuclear density profile. The data [233] suggest σ _abs = 4.2 mb. The generalization of Eq. (7.71) to the nucleus-nucleus case [235] gives a good description of the J∕ Ψ suppression (relative to binary pp scaling) in S+U and peripheral Pb+Pb collisions at top SPS energy [226]. It has thus become customary to quantify the J∕ Ψ suppression in central A+A collisions by relating the observed yield, not directly to the scaled pp yield (thus obtaining R _AA), but to a hypothetical “normal absorption” yield baseline, established by Eq. (7.71). All further absorption is called “anomalous suppression”.

Figure 7.54 shows the results gathered at $\sqrt {s} = 17.3$ GeV by the NA38–NA50–NA60 di-muon spectrometer [236], for minimum bias S+U ($\sqrt {s}= 20$ GeV), In+In and Pb+Pb. Up to N _part ≈ 100 all yields gather at the “normal absorption” expectation from p+A scaling. A plateau at 0.8 follows for intermediate N _part values up to about 200 (which corresponds to central In+In collisions, so the NA60 data end here), and a final falloff toward 0.6 for central Pb+Pb collisions. It appears natural to interpret the former step as an indication of Ψ^′ suppression, the final step as χ _c dissociation. No genuine J∕ Ψ suppression is indicated. The expectation from lattice calculations [232] that J∕ Ψ dissociation does not occur until T ≈ 2 T _c (and, thus, 𝜖 ≈ 16 𝜖 _c) is thus compatible with Fig. 7.54. We know from Eq. (7.70) that T ≤ 1.3 T _c at top SPS energy. The data are thus compatible with no break-up of the J∕ Ψ at the SPS, unlike at top RHIC energy where one expects T ≈ 2T _c [61, 96].

Fig. 7.54

J∕ Ψ production measured in minimum bias collisions of S+U at $\sqrt {s}=20$ GeV and Pb+Pb and In+In at $\sqrt {s}=17.3$ GeV. The yield is scaled by “normal nuclear absorption”, Eq. (7.71) [236]

The RHIC data obtained by PHENIX [237] are shown in Fig. 7.55. Minimum bias Au+Au collisions are covered at mid-rapidity, as well as at 1.2 < y < 2.2, and plotted vs. N _part. Due to a parallel measurement of J∕ Ψ production in p+p collisions [238] the PHENIX experiment is in the position to show R _AA, but this is done without re-normalization to p-A absorption. J∕ Ψ is suppressed in central collisions, R _AA ≤ 0.2. Note that R _AAcannot drop down below about 0.15, due to unsuppressed surface contributions. The suppression is thus stronger than at top SPS energy³—in fact it is almost maximal. We conclude that in central Au+Au at $\sqrt {s} = 200$ GeV the charmonium signal gets significantly quenched, in accord with the inferences about the primordial temperature that we presented in Sects. 7.2.5 and 7.4, to amount to about 300 MeV, i.e. T∕T _c ≈ 2 as implied for J∕ Ψ dissociation by the lattice calculations [232].

Fig. 7.55

R _AA for J∕ Ψ production in minimum bias Au+Au collisions at $\sqrt {s}=200$ GeV, by PHENIX [237] at mid-rapidity and at 1.2 < y < 2.2

The above interpretation is still a matter of controversy [239]. It remains unclear whether successive, distinct stages of normal and anomalous J∕ Ψ suppression are compatible with the dynamical evolution in central A+A collisions. A further open question refers to the difference in Fig. 7.55 of the $\left <y\right >= 0$ and $\left <y\right >= 1.7$ data at intermediate centrality [239] interpretation of which should be suspended until the advent of higher statistics data.

A different aspect of charmonium production in A+A collisions requires attention: at the stage of universal hadronization a certain fraction of bound $c \overline {c}$ mesons results, as the outcome of the density of uncorrelated c and $\overline {c}$ quarks in the QGP medium as it enters hadronization [240, 241]. The stage of statistical hadronization (recall Sect. 7.3) is omitted in the charmonium suppression models [41, 230, 234, 235], which proceed in two steps (only): primordial nucleon-nucleon collisions produce an initial input of $c \overline {c}$ pairs, proportional to $\sigma _{c \overline {c}}^{\mathrm {NN}} \times N^{\text{AA}}_{\text{coll}} \: (b)$. In vacuum, the low relative momentum fraction of these $c \overline {c}$ pairs (about 1%) would evolve into charmonium hadrons, after a formation time of several fm/c. In the concurrently developing QGP medium, however, the initial $c \overline {c}$ correlated pairs may dissociate owing to the absence (due to color screening [41]) of vacuum-like bound states [232], at high T. At T ≥ 2 T _call fireball charmonium production would thus cease, all $c \overline {c}$ pairs ending up in singly charmed hadrons. This picture [ 230] is incomplete.

Even if all $c \bar {c}$ pairs break up at RHIC during the early phase of central collisions, the single charm and anti-charm quarks flow along in the expanding medium of equilibrated light and strange quarks. This picture is supported [94] by the observed elliptic flow of charm merging into the universal trend. Charm cannot, however, be chemically (flavor) equilibrated at the low plasma temperature, where it is essentially neither newly created nor annihilated [241]. The initially produced c and $\overline {c}$ quarks (a few per central Au+Au collision at RHIC, a few tens at LHC) finally undergo statistical hadronization at T = T _c along with all other light and strange quarks. To deal with the non-equilibrium overall charm abundance an extra charm fugacity factor γ _c is introduced into the statistical model [108] calculation (for details see [241]). J∕ Ψ and Ψ^′ are thus created in non-perturbative hadronization, with multiplicities proportional to $\gamma ^2_{\mathrm {c}}$ and phase space weights, along with all other charmed hadrons. This “regeneration” model also agrees with the RHIC data of Fig. 7.55, albeit within a large systematic uncertainty [241].

We note that the term regeneration is, in fact, misleading. The statistical hadronization process does not recover the initial, small fraction of correlated $c \overline {c}$ pairs that would end up in J∕ Ψ in vacuum. It arises from the total density of primordially produced c and $\overline {c}$, uncorrelated in the hadronizing fireball volume.

The statistical hadronization J∕ Ψ production process, sketched above, thus has the unfortunate property of providing a trivial background charmonium yield, unrelated to the deconfinement signal [41] referring to the primordial J∕ Ψ yield. Only about 1% of the primordial $c \overline {c}$ yield results in charmonia, in vacuum. The in-medium deconfinement process breaking up the $c \overline {c}$ correlation on its way to charmonia, thus constitutes a mere 1% fraction of the total charmed quark and anti-quark number. The regeneration process is insensitive to this 1% fraction, deconfined or not. At T _c, charm hadronization reacts only to the total abundance of c and $\overline {c}$, as imprinted into the dynamical evolution by the perturbative QCD $c \overline {c}$ production rate of initial nucleon-nucleon collisions. At RHIC, it turns out [241] that the c and $\overline {c}$ density is low, giving rise to substantial canonical suppression (recalling Eqs (7.38)–(7.42) in Sect. 7.3) of the two charm quark charmonia, relative to D mesons, during hadronization. With a tenfold $c, \: \overline {c}$ density at LHC, grand canonical charmonium production will set in, thus probably overshooting the primordial yield reference, $\sigma _{\mathrm {NN}}^{J/\Psi } \times N_{\text{coll}}$. Thus we expect R _AA > 1 at the LHC. The role of a critical deconfinement “thermometer” is lost for J∕ Ψ at LHC, but the bottonium Y  states can take over, being deconfined well above T = 300 MeV [242].

The RHIC result [237] for J∕ Ψ in central Au+Au collisions (Fig. 7.55), namely that R _AA → 0.2, represents the lucky coincidence that the initial temperature, T ≈ 300 MeV, is high enough to dissolve the correlated $c \overline {c}$ charmonium precursor states, while the J∕ Ψ suppression is not yet overshadowed by the trivial hadronization yield of J∕ Ψ.

7.6.2 Direct Photons

Photons are produced during all stages of the dynamical evolution in A+A collisions. About 98% stem from final electromagnetic hadron decays, not of interest in the present context, other then by noting that their rate has to be painstakingly measured experimentally, in order to obtain “direct” photon spectra at low p _T by subtracting the decay fraction from the total. This was done [224] by WA98 in central Pb+Pb collisions at top SPS energy; we show their result in Fig. 7.56.

Fig. 7.56

The WA98 direct photon transverse momentum spectrum for central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV. Also indicated are scaled pA results above 2.0 GeV/c and pQCD estimates [243]. From [224]

Only upper limits could be obtained at p _T ≤ 1.5 GeV/c due to overwhelming background from π ⁰ and η decay, thus also obscuring the major spectral domain in which to look for a direct photon QCD plasma black body radiation source, i.e. for thermal photons of a fireball at T between T _c and about 250 MeV [223]. Several data from p+p and p+A collisions at nearby $\sqrt {s}$ and scaled up to central Pb+Pb are included in Fig. 7.56, at p _T ≥ 2 GeV/c, and one sees the Pb+Pb data in clear excess of such contributions from primordial bremsstrahlung and hard, pQCD initial partonic collisions [243]. This excess ranges up to about 3.5 GeV/c, in Fig. 7.56. Above, the hard pQCD initial collision yield dominates [244] over thermal production.

In contrast to all other primordial high p _T pQCD yields (e.g. J∕ Ψ, charm, jet leading partons) this photon yield is not attenuated in the medium of A+A collisions. We have shown in Fig. 7.44 the R _AA for the PHENIX central Au+Au direct photon results [181] at RHIC $\sqrt {s}=200$ GeV, obtained in a background substraction procedure [245] similar to the one undertaken by WA98. This procedure gives reliable data at p _T > 4.0 GeV/c, at RHIC, and we observe R _AA = 1. Hard initial photons are not attenuated, and there is no sign of any other direct photon contribution besides the primordial pQCD yield which, in fact, is shown (by R _AA = 1) to obey binary scaling. However, there is no hint to plasma thermal radiation (except for a trend at the very limit of statistical significance, at p _T < 4.5 GeV/c) in this high p _T window.

The WA98 SPS data, with thermal radiation enhancement indicated in the interval 1.5 < p _T < 3.5 GeV/c, thus remained as the sole evidence until, more recently, the PHENIX experiment gained low p _T data [246] exploiting the fact that any source of real photons emits also virtual photons γ ^∗ leading to internal conversion to an e ⁺e ⁻ pair (the Dalitz effect). To identify this yield the invariant mass distribution of e ⁺e ⁻ pairs is analyzed outside the phase space limits of π ⁰ Dalitz decay; the decay pairs of all remaining hadron sources (η,  Δ) is subtracted as a “cocktail”. The remaining pair yield is then converted assuming $\gamma ^*_{\text{dir}}/\gamma ^*_{\text{inclusive}}= \gamma _{\text{dir}}/\gamma _{\text{inclusive}}$ (see ref. [246] for detail), thus finally obtaining data representative of γ _dir in this approach. Figure 7.57 shows the corresponding p _T distribution which covers the interval 1.3 ≤ p _T ≤ 4.5 GeV/c, within which the conventional direct photon extraction method did not give significant results [181]. The PHENIX experiment has also obtained direct photon spectra in p+p and d+Au at $\sqrt {s}=200$ GeV [247] which are both well accounted for [246] by a next to leading order (NLO) pQCD photon production model [248]. These data were already employed in deriving R _AA = 1 for central Au+Au collisions, as shown in Fig. 7.44 and referred to, above. The pQCD fits derived from p+p and d+A are shown in Fig. 7.57 after binary scaling to Au+Au (pQCD × T _AA). They merge with the yield at p _T ≥ 4 GeV/c but demonstrate a large excess yield below 3 GeV/c. That excess is well described by adding a thermal photon component resulting from the hydrodynamic model of d’Enterria and Peressounko [249]. It traces the dynamical evolution during the early stages of equilibrium attainment, in which the photon luminosity of the emerging QGP matter phase is maximal. The hydrodynamic model provides for the space-time evolution of the local photon emission rate [223] which includes hard thermal loop diagrams to all orders, and Landau-Migdal-Pomeranchuk (LPM) in-medium interference effects. Similar, in outline, to previous models that combined algorithms of plasma photon radiation luminosity with hydrodynamic expansion [250], the model [249] fits the data in Fig. 7.57. It implies a picture in which the early stage of approach toward thermal equilibrium at RHIC is governed by a symbolic, initial, effective “temperature” of about 550 MeV which, after equilibration at t ≈ 0.6 fm/c, corresponds toT ≈ 360MeV in the primordial plasma [249]: close to the consensus about initial T as derived from J∕ Ψ suppression, jet attenuation, elliptic flow and transverse energy coupled with the 1-dimensional Bjorken expansion model.

Fig. 7.57

Internal conversion measurement of direct photons in central Au+Au collisions at 200 GeV [246]. Predictions by pQCD [248] and thermal hydrodynamic [249] models are included

However, we note that the employed theoretical framework, hard thermal loop (HTL) QCD perturbation theory of a weakly coupled plasma state, as combined with hydrodynamics, has a tendency to call for rather high initial T values. This applies both to the above analysis [249] of RHIC data which is based on the thermal field theory model of Arnold, Moore and Yaffe [223], and to previous analysis [250] of the WA98 SPS data of Fig. 7.56. Direct photon production is even more strongly biased toward the primordial, high T evolution than jet attenuation (that may be proportional to T ³ [212]). Thus, by implication of the model [249] that fits the low p _T RHIC data of Fig. 7.57, the yield is highly sensitive to the (pre-equilibrium) formation period, 0.15 < t < 0.6 fm/c, where the HTL model might not be fully applicable. This illustrates the present state of the art. The model(s) based on perturbative QCD require extreme initial “temperatures” to produce the high photon yield, indicated by the RHIC experiment. The strongly coupled nature [213] of the non perturbative local equilibrium QGP state at RHIC, T ≈ 300 MeV, may provide for an alternative approach to plasma photon production.

7.6.3 Low Mass Dilepton Spectra: Vector Mesons In-medium

We have dealt with dilepton spectra throughout the above discussion of J∕ Ψ and direct photon production, as messenger processes sensitive to the energy density prevailing (during and) at the end of the primordial equilibration phase. The third tracer observable, low mass vector meson dilepton decay in-medium, samples—on the contrary—the conditions and modalities of hadron deconfinement in the vicinity of T = T _c. SPS energy is ideally suited for such studies as the QGP fireball is prepared near T _c whereas, at RHIC, it races through the T _c domain with developed expansion flow. The major relevant data thus stem from the CERN SPS experiments NA45 [251] and NA60 [136], which have analyzed e ⁺e ⁻ and μ ⁺μ ⁻ production at invariant mass from 0.2 to 1.4 GeV.

Figure 7.58 shows NA45 data [251] for e ⁺e ⁻ production in central Pb+Au collisions at $\sqrt {s}=17.3$ GeV. In searching for modifications of ϱ properties and of π ⁺π ⁻ annihilation via virtual intermediate ϱ decay to e ⁺e ⁻, in the high density environment near the hadron-parton coexistence line at T = T _c, the various background sources have to be under firm control. The Dalitz decays of π ⁰, η and η ^′ and the in vacuo e ⁺e ⁻ decays of ϱ, ω and Φ, which occur after hadronic freeze-out to on-shell particles, form a hadronic “cocktail” (left panel in Fig. 7.58) that is generated from yields provided by the grand canonical statistical model [108]. Within detector resolution, π, ω and Φ leave distinct peaks but the observed invariant mass distribution is not accounted for.

Fig. 7.58

Di-electron mass spectrum for central Pb+Au collisions at $\sqrt {s}=17.3$ GeV with the hadron decay cocktail (left) and further in medium contributions (right) [251]; see text for detail

One needs also to account for background from Drell-Yan lepton pair production and open charm decay, both scaling with “number of collisions” A ^4∕3. The latter contribution arises from primordial $c \overline {c}$ charm production, $\left <c\right >=\left <\overline {c}\right >$ which leads to synchronous formation of $\left <D\right >=\left <\overline {D}\right >$ at hadronization; subsequent decays D → lepton + X, $\overline {D} \rightarrow$ antilepton + Y create $L \overline {L}$ pairs. This procedure is straight forward as no significant medium attenuation occurs besides the statistical charm redistribution conditions at hadronization (Sect. 7.6.1), governing $D, \overline {D}$ production [241].

Onward to non-trivial backgrounds in the invariant mass plot of Fig. 7.58, we recall the presence of thermal lepton pairs from virtual photon production in the early plasma phase, in parallel to real “direct” photon emission [252]. The spectrum of such pairs contains an average decay factor $\exp \, (M_{ll} / T)$, with T the (initial) plasma temperature. With T ≥ 220 MeV assumed for top SPS energy [43, 44], this contribution is a background candidate over the entire invariant mass interval covered by the data. In general Drell-Yan, open charm decay and plasma radiation contributions are smooth, partially closing the “holes” in the hadronic cocktail undershoot of the data. This smoothing effect is helped, finally, by consideration of modifications concerning the ϱ meson spectral function near T = T _c, which [133,134,135] both affects the immediate ϱ → e ⁺e ⁻ decay invariant mass region (through the fraction of in-medium ϱ decays vs. the in vacuum decay fraction after hadronic freeze-out) and, even more importantly, the contribution of in-medium π ⁺π ⁻ annihilation to dileptons. The latter contribution accounts for the most obvious deviation between cocktail and data at 0.3 ≤ m _ll ≤ 0.7 GeV in Fig. 7.58 (left panel).

The right hand panel of Fig. 7.58 shows the results of various theoretical models which address the sources of the significant dilepton excess over hadronic (in vacuum) and Drell-Yan cocktails, labeled “Rapp-Wambach” [133, 135], “dropping mass” (Brown-Rho [134]) and “Kaempfer” [252]. We shall return to these models below but note, for now, that the extra yield in central A+A collisions chiefly derives from π ⁺π ⁻ annihilation via the (in medium modified) ϱ resonance, and from modification of the ϱ peak itself.

With improved statistics and background control, the A+A specific extra dilepton yield below M ≈ 1.4 GeV/c ² can be represented by itself, after cocktail subtraction. This has been first accomplished by NA60 [136, 253] and, more recently, also by NA45 [254]. We show the former results in Fig. 7.59. The left panel shows the di-muon invariant mass spectrum in semi-central Indium-Indium collisions at top SPS energy $\sqrt {s}=17.3$ GeV, compared to the hadronic cocktail, qualitatively in agreement with the left hand panel of Fig. 7.58 but with superior resolution and statistics. The cocktail subtraction procedure (see [136] for details) leads to an invariant mass spectrum of di-muon excess in In+In, shown in the right side panel of Fig. 7.59: an experimental landmark accomplishment. The ϱ vacuum decay contribution to the hadronic cocktail has been retained and is shown (thin solid line) to be a small fraction of the excess mass spectrum, which exhibits a broad distribution (that is almost structureless if the cocktail ϱ is also subtracted out), widening with collision centrality [136]. The best theoretical representation of the excess yield again results (like in Fig. 7.58, right panel) from the broadening model [133, 135, 255] where the ϱ spectral function is smeared due to various coupling mechanisms within the medium via the vector dominance model, prior to hadronic freeze-out. In the VDM ϱ couples, both, to pion pair annihilation, and to excited baryon states like the N ^∗ (1520), via their Nππ decay branches.

Fig. 7.59

(Left) Di-muon invariant mass spectrum in semi-central In+In collisions at $\sqrt {s}=17.3$ GeV, with hadron final state decay cocktail. (Right) Excess mass spectrum after cocktail subtraction, confronted with fits from the broadening [133, 135, 255] and the dropping mass [228] models. From [136]

The above data still imply serious conceptual questions. It is unclear to exactly which stage of the dynamical evolution (in the vicinity of T = T _c) the excess dilepton yield should correspond. As the observations appear to be coupled to in-medium ϱ meson “metabolism” we need to identify a period of temporal extension above the (in vacuo) ϱ half life (of 1.3 fm/c), safely 2 fm/c. This period should be located in the vicinity of hadro-chemical freeze-out. From top SPS to RHIC energy, hadro-chemical freeze-out should closely coincide with hadron formation, i.e. it should occur near the parton-hadron coexistence line, at T = T _c. The microscopic parton cascade model of reference [85] implements the Webber [121] phenomenological, non-perturbative QCD hadronization model (recall Sect. 7.3.3) which proposes pre-hadronization clusters of color neutralization (Fig. 7.31) as the central hadronization step. In it, so one might speculate, the transition from pQCD to non perturbative QCD creates the chiral condensates $\left <q \overline {q}\right >$, spontaneously breaking chiral symmetry [256] (see below), and creating hadronic mass. The overall process, from pQCD color neutralization to on-shell hadrons, takes about 2.5 fm/c [85, 86] at top SPS energy. This could, thus, be the period of excess dilepton yield creation. However, the relation of the models employed above [133,134,135, 255, 256] to this primordial spontaneous creation of chiral condensates is still essentially unknown [256].

Thus, at present, the 1990s paradigm of a direct observation of the chiral phase transition in QCD has been lost. The Brown-Rho model [134] predicted the ϱ mass to drop to zero at T = T _c, occurring as a certain power of the ratio $\left <q \overline {q}\right >^{\text{med}}/\left <q \overline {q}\right >^{\text{vac}}$ of the chiral condensate in medium and in vacuum which approaches zero at the chiral phase transition temperature, then expected to coincidence with the deconfinement temperature. This “dropping mass” model is ruled out by the data in Fig. 7.58 and 7.59. This is, perhaps, a further manifestation of the fact that the deconfined QGP state at T ≥ T _c is not a simple pQCD gas of quarks and gluons [213]. In fact, lattice calculations [232, 257] find indications of surviving light $q \overline {q}$ pair correlations in the vector channel at T ≥ T _c. Thus the two most prominent symmetries of the QCD Lagrangian, non abelian gauge invariance (related to confinement) and chiral invariance (related to mass) might exhibit different critical patterns at T = T _c and low baryo-chemical potential. This conjecture is best illustrated by the observation that the broad, structureless NA60 excess dilepton spectrum of Fig. 7.59 (after cocktail ϱ subtraction) is equally well reproduced by a T ≈ 160–170 MeV calculation in hadronic (equilibrium) matter [133, 253, 254], and by a thermal QGP fireball of $q \overline {q}$ annihilation at this average temperature [252], as illustrated here by the model curve labeled “Kaempfer” in Fig. 7.58 (right panel). This observation has invited the concept of parton-hadron duality near T _c [258], which might be provocatively translated as “the QCD chiral transition properties cannot be unambiguously disentangled from the deconfinement transition effects at T _c” [256].

We may be looking at the wrong domain of [T, μ _B] space: too high $\sqrt {s}$ and, thus, too high T, too low μ _B. Already at top SPS energy the medium is dominated by the deconfinement, not by the chiral QCD transition. After hadronization the medium is still at T close to T _c but the density drops off within a few fm/c, not allowing for an equilibrium mean field state of chirally restored hadrons. It is thus perhaps not surprising that the data are seen to be dominated by simple broadening and lack of structure: perhaps that is all that happens to hadrons at T _c.

The chiral restoration transition should thus be studied at higher μ _B and lower T such that the dynamics achieves high baryon densities but still merely touches the critical (deconfinement) temperature. In fact, at μ _B → 1 GeV and T < 100 MeV the chiral transition should be of first order [259]. Here, in fact, the chiral condensate mass plays the role of the order parameter (in analogy to the magnetization in a spin system), which approaches zero as T → T _c. We might thus speculate that, unlike at top SPS to LHC energy (where deconfinement dominates), the chiral QCD first order phase transition will dominate the phenomena occurring near the hadron-parton borderline, in the vicinity of $\sqrt {s}=4$–6 GeV [142]. This requires a new experimental program, with low energy running at the SPS [260], at RHIC [261] and at the GSI FAIR project [262].

7.7 Fluctuation and Correlation Signals

Fluctuation and correlation signals in A+A collisions can be evaluated in single events, due to the high multiplicity of produced particles. Depending on the physics context we may be interested to see either a small, or a large nonstatistical fluctuation effect. For example in view of the universality of hadronization (Sect. 7.3) we would have difficulty with an event by event pion to baryon ratio (essentially $\mu _{\mathrm {B}}^{-1}$) fluctuating by, say, 50%. Conversely, searching for critical fluctuations in the vicinity of a predicted critical point of QCD [146, 147] we would be frustrated if event-wise $\left <p_{\mathrm {T}}\right >$, d N∕d y (low p _T pion) [263] or strange to non-strange ratios like K∕π [148, 264] would not exhibit any significant fluctuation beyond statistics. Overall, event by event fluctuation observables also carry a message concerning the robustness of our assumptions about equilibrium attainment. It turns out that equilibrium properties are not, merely, central limit consequences of ensemble averaging. Rather to the contrary, each A ≈ 200 central collision event at $\sqrt {s} \ge 10$ GeV appears to offer, to the dynamical evolution of bulk properties, a sufficiently complete macroscopic limit. Such that we can view the event-wise bulk dynamics as “self analyzing”.

7.7.1 Elliptic Flow Fluctuation

That this ascertations is far from trivial is illustrated in Fig. 7.60. It shows [265] the primordial transverse energy density projection (the stage basic to all primordial observables) at t ≈ 0.2 fm/c, in a central Au+Au collision at $\sqrt {s}=200$ GeV, exhibiting an extremely clumpy and nonhomogeneous structure, apparently far away from equilibrium.

Fig. 7.60

Initial transverse energy density distribution of a single central Au+Au collision event at $\sqrt {s}=200$ GeV [265]

The imaging of this initial geometrical pattern of the collision volume by a hydrodynamic evolution even applies at the level of individual events, such as illustrated in Fig. 7.60. The PHOBOS Collaboration has shown [266,267,268] that an event by event analysis of the elliptic flow coefficient v ₂ is possible (see ref. [266] for detail), by means of a maximum likelihood method. For initialization they sample the seemingly random initial spatial density distribution of single Au+Au collision events by the “participant excentricity” of individual Monte Carlo events,

$$\displaystyle \begin{aligned} \epsilon_{\text{part}} = \frac{\sqrt{(\sigma_y^2 - \sigma_x^2)^2 + 4 \sigma_{xy}^2}}{\sigma_y^2+ \sigma_x^2} {} \end{aligned} $$

(7.72)

where $\sigma _{xy}= \left <xy\right >-\left <x\right >\left <y\right >$. The average values of 𝜖 _part turn out to be similar to 𝜖 _x from Eq. (7.47), as expected, but the relative fluctuation width $\sigma (\epsilon )/\left <\epsilon \right >_{\text{part}}$ turns out to be considerable. It is the point of this investigation [267, 268] to show that the observed relative event by event flow fluctuation equals the magnitude of the relative excentricity fluctuation. This is shown [268] in Fig. 7.61. The left panel demonstrates that the average $\left <v_2\right >$ obtained vs. N _part from the event-wise analysis agrees with the previously published [156] event-averaged PHOBOS data. The right panel shows that the event-wise relative fluctuation of v ₂ is large: it amounts to about 0.45 and is equal to the relative fluctuation of 𝜖 _part, i.e.

$$\displaystyle \begin{aligned} \sigma(v_2)/\left<v_2\right>\approx \sigma (\epsilon_{\text{part}})/\left<\epsilon_{\text{part}}\right>. {} \end{aligned} $$

(7.73)

The initial geometry appears to drive the hydrodynamic evolution of the system, not only on average but event-by-event [268], thus providing for an example of the self-analyzing property mentioned above. The v ₂ signal thus emerges as the most sensitive and specific diagnostic instrument for the primordial conditions and their subsequent evolution: it reveals even the random (Fig. 7.60) initial fluctuations. In comparison the analysis with thermal photons is only sensitive to the primordial temperature [249], and restricted by very small cross sections and significant background from other sources and evolution times. It also does not give viscosity information.

Fig. 7.61

(Left) Event by event elliptic flow analysis by PHOBOS gives an average $\left <v_2 \right >$ that agrees with the result of ensemble analysis, in Au+Au at 200 GeV, for charged hadrons. (Right) Event-wise relative v ₂ fluctuation vs. N _part, compared to the event-wise relative fluctuation of the participant excentricity, $\sigma (\epsilon _{\text{part}})/ \left <\epsilon _{\text{part}} \right >$. The closed line gives v ₂ variation due to N _part number fluctuation. From [268]

7.7.2 Critical Point: Fluctuations from Diverging Susceptibilities

Recalling the goal defined in the introduction we seek observables that help to elaborate points or regions of the QCD phase diagram, Fig. 7.1. We have seen several observables that refer to the QCD plasma environment at T ≥ 300 MeV, μ ≈ 0 (elliptic flow, jet attenuation, J∕ Ψ suppression, direct photon production), which could be first resolved within the primordial time interval τ ≤ 1 fm/c accessible at RHIC energy. The LHC will extend the reach of such observables toward T ≈ 600 MeV, x _F ≤ 10⁻³, at μ _B = 0. On the other hand, relativistic A+A collisions at lower energy permit a focus on the hypothetical QCD parton-hadron coexistence line, T = T _c (μ _B), with the domain μ _B → 500 MeV being accessible at the SPS. Characteristic observables are radial flow, hadro-chemical freeze-out, and chiral symmetry restoration effects in dilepton vector meson spectra. Focusing on this domain, we discuss fluctuations potentially associated with the existence of a critical point [8,9,10,11, 146, 147].

At the end of Sect. 7.6.3 we mentioned the conclusion from chiral symmetry restoration models [15, 259] that at high μ _B the phase transformation occurring at T _c (μ _B) should be a chiral first order phase transition. On the other hand, lattice QCD has characterized [16] the phase transformation at μ _B → 0, to be merely a rapid cross-over. Thus, the first order nature of the phase coexistence line in Fig. 7.1 has to end, with decreasing μ _B, in a QCD critical point, tentatively located by recent lattice QCD calculations [9,10,11] in the interval μ _B = 300–500 MeV. The existence of such a point in the [T, μ _B] plane would imply fluctuations analogous to critical opalescence in QED [146, 147, 263]. Beyond this second order phase transition point the coexistence line would be the site of a rapid cross-over [16]. This overall theoretical proposal places potential observations related to the critical point itself, and/or to the onset of first order phase transition conditions at higher μ _B, within the domain of the lower SPS energies, $\sqrt {s} \le 10$ GeV. Note that, at such low energies, the initialization of thermal equilibrium conditions should occur in the vicinity of T _c, unlike at RHIC and LHC, and that the central fireball spends considerable time near the coexistence line, at 300 ≤ μ _B ≤ 500 MeV.

To analyze potential observable effects of a critical point, we recall briefly the procedure in finite μ _B lattice theory that led to its discovery. One method to compute thermodynamic functions at μ _B > 0 from the grand canonical partition function Z(V, T, μ _q) at μ _q = 0 is to employ a Taylor expansion with respect to the chemical quark potential [10, 11, 270], defined by the derivatives of Z at μ = 0. Of particular interest is the quark number density susceptibility,

$$\displaystyle \begin{aligned} \chi_{\mathrm{u,d}} = T^2 \left(\frac{\delta^2}{\delta(\mu/T)^2} \: \frac{p}{T^4} \right) {} \end{aligned} $$

(7.74)

which can also be written as

$$\displaystyle \begin{aligned} \chi_{\mathrm{q}} = T^2 \left(\frac{\delta}{\delta(\mu_{\mathrm{u}}/T)} + \frac{\delta}{\delta(\mu_{\mathrm{d}}/T)} \right) \: \frac{n_{\mathrm{u}}+n_{\mathrm{d}}}{T^3} {} \end{aligned} $$

(7.75)

with χ _q = (χ _u + χ _d)∕2 and quark number densities n _u, n _d. We see that the susceptibility refers to the quark number density fluctuation. The lattice result [10, 270] is shown in Fig. 7.62, a calculation with two dynamical flavors assuming T _c = 150 MeV and three choices of chemical quark potential, μ _q = 0, 75 and 150 MeV, respectively, corresponding to μ _B = 3 μ _q = 0, 225 and 450 MeV. These choices correspond to LHC/RHIC energy, top SPS energy and $\sqrt {s} \approx 6.5$ GeV, respectively. At μ _B = 0 one sees a typical smooth cross-over transition at T = T _c whereas a steep maximum of susceptibility occurs with μ _B = 450 MeV. This suggests the presence of a critical point in the (T, μ _B) plane [270] in the vicinity of (150 MeV, 450 MeV). For final confirmation one would like to see this maximum disappear again, toward μ _q > T _c, but this is beyond the convergence domain of the employed Taylor expansion (see ref. [9] for alternative approaches).

Fig. 7.62

Quark number density susceptibility vs. temperature for light quarks in 2 flavor lattice QCD at finite μ _B. The calculation refers to T _c = 150 MeV and quark chemical potential μ _q∕T _c = 0, 0.5 and 1.0, respectively [270]. Smooth lines interpolate the calculated points; error bars indicate lattice statistics

From Fig. 7.62 we also expect a divergence of the strangeness susceptibility, for which no results from a 3 dynamical flavors calculation at finite μ _B exist to date. A lattice calculation at μ _B = 0, T ≈ 1.5 T _c suggests [271] that the u, d, s quark flavors densities fluctuate uncorrelated (but we do not know whether that is also true at $\mu _{\mathrm {B}}=\mu _{\mathrm {B}}^{\text{crit}})$. This could thus be observed in event by event analysis, in particular as a fluctuation of the Wroblewski ratio $\lambda _s = 2(s + \overline {s})/(u + \overline {u} + d + \overline {d})$ which is approximated by the event-wise ratio (K ⁺ + K ⁻)∕(π ⁺ + π ⁻). This was first measured by NA49 in central collisions of Pb+Pb at top SPS energy; the result [272] is shown in Fig. 7.63. The data result from a maximum likelihood analysis of track-wise specific ionization in the domain 3.5 ≤ y ≤ 5 slightly forward of mid-rapidity. The width σ _data is almost perfectly reproduced by the mixed event reference, such that the difference,

$$\displaystyle \begin{aligned} \sigma_{\text{dyn}} = \sqrt{(\sigma^2_{\text{data}} \: - \: \sigma^2_{\text{mix}})} {} \end{aligned} $$

(7.76)

amounts to about 3% of σ _data only, at $\sqrt {s}=17.3$ GeV. This analysis has more recently been extended to all energies available thus far, at the SPS [273] and at RHIC [274]. Figure 7.64 shows that σ _dyn stays constant from top SPS to top RHIC energy but exhibits a steep rise toward lower energies that persists down to the lowest SPS energy, $\sqrt {s}=6.2$ GeV. Figure 7.33 shows [107] that at this energy μ _B = 450 MeV, thus corresponding to the susceptibility peak in Fig. 7.62. Again, as we noted about the peak in Fig. 7.62: if these data indicate a critical point effect in the vicinity of μ _B = 450 MeV the relative fluctuation should decrease again, toward yet higher μ _B and lower $\sqrt {s}$. These data will, hence, be re-measured and extended to lower $\sqrt {s}$ by experiments in preparation [260,261,262] at CERN, RHIC and GSI-FAIR. This will also help to evaluate alternative tentative explanations invoking fluctuating canonical suppression [120], or strangeness trapping [275]. Finally, the position of the critical point needs to be ascertained by lattice theory.

Fig. 7.63

Event by event fluctuation of the K ⁺⁻∕π ⁺⁻ ratio in central collisions of Pb+Pb at $\sqrt {s}=17.3$ GeV, relative to mixed event background (histogram) [272]

Fig. 7.64

The relative deviation of the event by event K∕π fluctuation width from the mixed event background width, σ _dyn (see Eq. (7.76)); at SPS [273] and RHIC [274] energies

7.7.3 Critical Fluctuation of the Sigma-Field, and Related Pionic Observables

Earlier investigations of critical QCD phenomena that might occur in high energy nuclear collisions were based on QCD chiral field theory [276]. The QCD critical point is associated with the chiral phase transition in so far as it appears as a remnant of a tri-critical point [147] corresponding to the “ideal” chiral limit that would occur if m _u = m _d = 0. Therefore the existence of a second-order critical point, at μ _B > 0, is a fundamental property of QCD with small but non-zero quark masses [277]. The magnitude of the quark condensate, which plays the role of an order parameter of the spontaneously broken symmetry (generating hadronic mass), has the thermal expectation value

$$\displaystyle \begin{aligned} \left<\overline{q} q\right> = \frac{1}{Z} \sum_n \left<n \mid \overline{q} q \mid n \right>\exp (-E_n/T) {} \end{aligned} $$

(7.77)

with the partition function of hadronic states E _n

$$\displaystyle \begin{aligned} Z=\sum_n \exp(-E_n/T). {} \end{aligned} $$

(7.78)

The low energy behavior of the matrix elements $\left <n \mid \overline {q} q \mid n\right >$ can be worked out in chiral perturbation theory [277]. At the QCD critical point the order parameter fluctuates strongly. Its magnitude $\left <\overline {q} q\right >$ is identified with an isoscalar quantity, the so-called σ-field. The critical point communicates to the hadronic population via the σ ↔ ππ reaction, generating fluctuating fractions of the direct pion yield present near T = T _c, which thus gets imprinted with a fluctuation of transverse momentum (in the low p _T domain) stemming from σ mass fluctuation, downward toward the critical point. At it the isoscalar field ideally approaches zero mass, in order to provide for the long wavelength mode required by the divergence of the correlation length [147].

Note the relatively fragile structure of the argument. In an ideal, stationary infinite volume situation the sigma field would really become massless, or at least fall below the π ⁺π ⁻ threshold; thus its coupling to π ⁺π ⁻ becomes weak, and restricted to very small p _T. Furthermore, such primary soft pions, already small in number, are subject to intense subsequent re-absorption and re-scattering in the final hadronic cascade evolution [114]. In fact, experimental investigations of event by event p _T fluctuations in central A+A collisions, covering the entire $\sqrt {s}$ domain from low SPS to top RHIC energy have not found significant dynamic effects [278,279,280,281]. Figure 7.65 illustrates the first such measurement by NA49 [278] in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV, at forward rapidity 4 < y < 5.5, showing the distribution of event-wise charged particle average transverse momentum, a perfect Gaussian. It is very closely approximated by the mixed event distribution, ruling out a significant value of σ _dyn from Eq. (7.76). More sensitive measures of changes, event by event, in the parent distribution in transverse momentum space, have been developed [282, 283]. NA49 has employed [278, 279] the measure Φ(p _T), defined as [282]

$$\displaystyle \begin{aligned} \Phi (p_{\mathrm{T}}) = \sqrt{\frac{\left<Z^2\right>}{\left<N\right>}} - \sqrt{\overline{z^2}} {}\end{aligned} $$

(7.79)

where $z_i=p_{Ti}- \overline {p}_{\mathrm {T}}$ for each particle, with $\overline {p}_{\mathrm {T}}$ the overall inclusive average, and for each event Z =∑_Nz _i is calculated. With the second term the trivial independent particle emission fluctuation is subtracted out, i.e. Φ vanishes if this is all. Indeed, the data of Fig. 7.65 lead to Φ compatible with zero. Furthermore, a recent NA49 study [279] at mid-rapidity, covers the range from $\sqrt {s}=17.3$ to 6.3 GeV (where the K∕π ratio fluctuation in Fig. 7.64 exhibits the much-discussed rise, and even the ensemble average in Fig. 7.28 shows the unexplained sharp peak) but finds no significant Φ signal.

Fig. 7.65

Event by event fluctuation of average charged hadron p _T in the interval 4.0 < y < 5.5, in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV. Mixed event background given by histogram [278]

Alternatively, one can base a signal of dynamical p _T fluctuation on the binary correlation of particle transverse momenta in a given event, i.e. on the co-variance $\left <p_{Ti} \: p_{Tj}\right >$ [281, 283] of particles i, j in one event. Of course, the co-variance receives contributions from sources beyond our present concern, i.e. Bose-Einstein correlation, flow and jets (the jet activity becomes prominent at high $\sqrt {s}$, and will dominate the p _T fluctuation signal at the LHC). In co-variance analysis, the dynamical p _T fluctuation (of whatever origin) is recovered via its effect on correlations among the transverse momentum of particles. Such correlations can be quantified employing the two-particle p _T correlator [281, 284]

$$\displaystyle \begin{aligned} \left<\Delta p_{Ti} \: \Delta p_{Tj}\right> = \frac{1}{M_{\text{pairs}}} \: \sum^n_{k=1} \: \sum^{N(k)}_{i=1} \: \sum^{N(k)}_{j=i+1} \: \Delta p_{Ti} \Delta p_{Tj} {} \end{aligned} $$

(7.80)

where M _pairs is the total number of track pairs of the events k contained in the entire ensemble of n events, N(k) is the number of tracks in event k, and $\Delta p_{Ti}=p_{Ti}- \overline {p}_{\mathrm {T}}$ where $\overline {p}_{\mathrm {T}}$ is the global ensemble mean p _T. The normalized dynamical fluctuation is then expressed [281] as

$$\displaystyle \begin{aligned} \sigma (p_{\mathrm{T}})_{\text{dyn}} = \sqrt{\left<\Delta p_{Ti} \: \Delta p_{Tj}\right>} \: / \: \overline{p_{\mathrm{T}}}. {} \end{aligned} $$

(7.81)

It is zero for uncorrelated particle emission.

Figure 7.66 shows the analysis of p _T fluctuations based on the p _T correlator, for central Pb+Au SPS collisions by CERES [280] and for central Au+Au at four RHIC energies by STAR [281]. The signal is at the 1% level at all $\sqrt {s}$, with no hint at critical point phenomena. Its small but finite size could arise from a multitude of sources, e.g. Bose-Einstein statistics, Coulomb or flow effects, mini-jet-formation, but also from experimental conditions such as two-track resolution limits [284]. We note that even if a critical opalescence effect, related to a fluctuating chiral condensate at T = T _crit, couples to the primordial, low p _T pion pair population [147, 285], this signal might be dissipated away, and thus “thermalized” to the thermal freeze-out scale of about 90–110 MeV, as a pion experiences about 6 re-scatterings during the hadronic cascade [114]. On the other hand the hadro-chemical K∕π ratio fluctuation (Fig. 7.64) would be preserved throughout the cascade (Sect. 7.3).

Fig. 7.66

Dynamical p _T event by event fluctuation analysis by σ(p _T)_dyn of Eq. (7.81), vs. $\sqrt {s}$, showing SPS [280] and RHIC [281] data

7.7.4 Bose-Einstein-Correlation

Identical boson pairs exhibit a positive correlation enhancement when $\Delta {\vec {p}_{ij}} \rightarrow 0$, an intensity correlation analogous to the historical Hanbury-Brown and Twiss effect (HBT) of two photon interferometry [286] employed in astrophysics. In nucleus-nucleus collisions this is an aspect of the symmetry of the N-pion wave function that describes pion pairs at the instant of their decoupling from strong interaction. The momentum space correlation function $C(q,K), \: q=p_1 - p_2, \: K = \frac {1}{2} (p_1+p_2)$ is the Fourier transform of the spatial emission function S(x, K) which can be viewed as the probability that a meson pair with momentum K is emitted from the space-time point x in the freezing-out fireball density distribution [96, 287].

The aim of HBT two particle interferometry is to extract from the measured correlator C(q, K) as much information about S(x, K) as possible. In addition to the traditional HBT focus on geometrical properties of the source distribution (“HBT radii”) there occurs information on time and duration of emission, as we have already employed in Fig. 7.19, illustrating τ _f and Δτ in central Pb+Pb collisions at top SPS energy [90]. Moreover, even more of dynamical information is accessible via the effects of collective flow on the emission function. In this respect, the observations make close contact to the hydrodynamic model freeze-out hyper-surface (Sect. 7.3.1) and the contained flow profiles. HBT thus helps to visualize the end of the collective radial and elliptic flow evolution. This implies that we expect to gather evidence for the, perhaps, most consequential property of A+A collisions at high $\sqrt {s}$, namely the primordially imprinted Hubble expansion.

We do not engage here in a detailed exposition of HBT formalism and results as comprehensive recent reviews are available [96, 287]. Briefly, the measured quantity in π ⁺π ⁺, π ⁻π ⁻ or K ⁺K ⁺ interferometry is the correlator

$$\displaystyle \begin{aligned} C(q,K) = \frac{{\mathrm{d}}^6 N/{\mathrm{d}}p^3_1 \; {\mathrm{d}}p_2^3}{{\mathrm{d}}^3N/{\mathrm{d}}p_1^3 \;\; {\mathrm{d}}^3N/{\mathrm{d}}p_2^3} {} \end{aligned} $$

(7.82)

of pair yield normalized to the inclusive yield product. The correlator is related to the emission function which is interpreted as the Wigner phase space density of the emitting source [288]:

$$\displaystyle \begin{aligned} C(q,K) \approx 1 + \frac{\mid \int {\mathrm{d}}^4x \; S(x,K) \; {\mathrm{e}}^{{\mathrm{i}} qx}\mid^2}{\mid \int {\mathrm{d}}^4 x \; S(x,K) \mid^2}. {} \end{aligned} $$

(7.83)

Due to the experimental on-shell requirement $K_0 = \sqrt {K^2+m^2}$ the 4-vector components of K are constrained on the left hand side. Thus, relation (7.83) cannot simply be inverted.

To proceed one employs a Gaussian ansatz on either side of Eq. (7.83). The experimental data are parametrized by source “radius” parameters R _ij(K),

$$\displaystyle \begin{aligned} C(q,K) = 1 + \lambda (K) \exp \: [ - \sum_{ij} R^2_{ij} (K) q_i q_j \: ] {} \end{aligned} $$

(7.84)

employing λ(K) essentially as a fudge factor (related nominally to possible coherence of emission effects in the source, which would dilute or remove the Bose-Einstein statistics effect of C → 2 for q → 0 but have never been seen in nuclear collisions). In Eq. (7.84) the sum runs over three of the four components of q, due again to the on-shell requirements [287]. For the emission function S(x, K) a Gaussian profile is assumed about an “effective source center” $\overline {x} (K)$, thus

$$\displaystyle \begin{aligned} S(x,K) \rightarrow S(\overline{x} (K), K) \: \times \: G {} \end{aligned} $$

(7.85)

where G is a Gaussian in coordinates $\tilde {x}^{\mu } (K)$ relative to the center coordinates $\overline {x}^{\mu } (K)$. Inserting Eq. (7.85) into (7.83) one finally obtains

$$\displaystyle \begin{aligned} C(q,K) = 1+ \lambda(K) \: \exp \: [ -q_{\mu} q_v \left<\tilde{x} ^{\mu} \: \tilde{x}^{\nu}\right> ] {} \end{aligned} $$

(7.86)

where $\left <\tilde {x} ^{\mu } \: \tilde {x}^{\nu }\right >$ are the elements of the space-time variance of the correlation function, which re-interpret the “radii” $R_{ij}^2$ in Eq. (7.84). Assuming azimuthal symmetry (central collisions), cartesian parametrizations of the pair relative momentum q coordinates (corresponding to fixation of the space-time variance in Eq. (7.84)) have been introduced by Yano, Koonin and Podgoretskii [289], and, alternatively, by Pratt [290]. The latter, out-side-longitudinal coordinate system has the “long” direction along the beam axis. In the transverse plane, the “out” direction is chosen parallel to K _T = (p _1T + p _2T)∕2, the transverse component of the pair momentum K. The “side” direction is then orthogonal to the out- and long-direction but, moreover, it has the simplest geometrical interpretation (see ref. [287] for detail), to essentially reflect the transverse system size [288]. The parameters of Eq. (7.86) are thus defined; as an example we quote, from identification of Eq. (7.84) with (7.86), the resulting geometrical definition of the “side” radius,

$$\displaystyle \begin{aligned} R_{\text{side}}^2 (K) =\left<\tilde{y}(K)^2\right>. {} \end{aligned} $$

(7.87)

Overall, this model of Fourier related correlators, C(q, K) the experimentally accessible quantity (see Eq. (7.82)), and S(x, K) the to-be-inferred spatial freeze-out fireball configuration, leads to the Gaussian ansatz [287]

$$\displaystyle \begin{aligned} \begin{array}{rcl} C(q,K) =1+ \lambda (K) \: \exp [-R^2_{\text{out}} (K) q_{\text{out}}^2 - R_{\text{side}}^2 (K) q^2_{\text{side}} - \\ R^2_{\text{long}} (K) q^2_{\text{long}} + \mbox{cross terms}] \end{array} \end{aligned} $$

(7.88)

which is fitted to the experimental correlation function (Eq. (7.82)). The experiment thus determines the variances R _out, R _side and R _long. In the so-called “local co-moving system” (LCMS), defined as the frame in which p _z,1 = −p _z,2, i.e. β _long = 0, we obtain in addition to Eq. (7.87)

$$\displaystyle \begin{aligned} \begin{array}{rcl} R_{\text{out}}(K)^2 &\displaystyle = &\displaystyle \left<(\tilde{x}(K) - \beta_{\mathrm{T}} \tilde{t}(K))^2\right> \\ R^2_{\text{long}}(K)&\displaystyle = &\displaystyle \left<\tilde{z}(K)^2\right> \end{array} \end{aligned} $$

(7.89)

and finally, for azimuthal symmetry in central collisions with $\left <\tilde {x}^2\right > \approx \left <\tilde {y}^2\right >$ we find the “duration of emission” parameter illustrated in Fig. 7.19 [90]:

$$\displaystyle \begin{aligned} \left<\tilde{t} \: ^2\right> \approx \frac{1}{\beta_{\mathrm{T}}} \: \left( R^2_{\text{out}} - R^2_{\text{side}} \right). {} \end{aligned} $$

(7.90)

The resulting reduction of the initial 8 coordinates of the meson pair stems, in summary, from the on-shell requirement, from azimuthal symmetry and from approximate Bjorken invariance in the LCMS system [287, 288]. One has to be aware of the latter idealizations. Note that in an expanding source all HBT parameters depend on K, the pair mean momentum (see below).

We make first use of the above parametrization in Fig. 7.67. From the purely spatial radii R _side and R _long one can define a mid-rapidity volume at pionic decoupling, $V_{\mathrm {f}}=(2 \pi ) ^{2/3} \: R^2_{\text{side}} \: R_{\text{long}}$ which is shown [291] at K = 0.2 GeV for central Pb+Pb and Au+Au collisions from AGS [292] via SPS [90, 293] to RHIC [294] energy. The upper panel shows the $\sqrt {s}$ dependence, the lower illustrates the dependence on the charged particle rapidity density dN _ch∕dy which one might intuitively expect to be related to the freeze-out volume [295]. We see, firstly, that the plot vs. $\sqrt {s}$ exhibits a non-monotonous pattern at the transition from AGS to SPS energies [287, 295], whereas the plot vs. dN∕dy rather features a rise toward a plateau that ends in a steep increase at RHIC energies. Second, the tenfold increase in charged particle rapidity density is reflected in only a doubling of the “volume” V _f.

Fig. 7.67

Coherence freeze-out volume V _f from π ⁻pair Bose-Einstein correlation analysis in central Au+Au and Pb+Pb collisions, (upper panel) plotted vs. $\sqrt {s}$, (lower panel) vs. mid-rapidity charged particle density dN ^ch∕dy [291]

The latter observation reminds us of the fact that the geometrical parameters obtained via the above analysis do not refer to the global source volume if that volume undergoes a collective Hubble expansion [96, 287]. A pion pair emitted with small relative momentum into the azimuthal direction $\vec {K}_{\mathrm {T}}$ is likely to stem (only) from the fraction of the expanding source that also moves into this direction. This coupling between position and momentum in the source becomes more pronounced, both, with increasing K _T and increasing sources transverse velocity β _T from radial expansion. We have seen in Fig. 7.24 that the latter increases dramatically with $\sqrt {s}$, such that the coherence volume V _f comprises a decreasing fraction of the total fireball. It should thus rise much more slowly than proportional to the global dN∕dy [96, 287].

A striking experimental confirmation of the Hubble expansion pattern in central A+A collisions is shown in Fig. 7.68. The illustrated HBT analysis of NA49 [90] at $\sqrt {s}=17.3$ GeV, and of PHOBOS [294] at $\sqrt {s}=200$ GeV, employs the alternative parametrization of the correlation function C(q, K) introduced [289] by Yano, Koonin and Podgoretskii (YKP). Without describing the detail we note that the YKP correlation function contains the “YK velocity” β _YK describing the source’s longitudinal collective motion in each interval of pion pair rapidity,

$$\displaystyle \begin{aligned} Y_{\pi \pi} = \frac{1}{2} \: \ln \left( \frac{E_1+E_2 + p_{z1} + p_{z2}}{E_1 + E_2 -p_{z1} - p_{z2}} \right). {} \end{aligned} $$

(7.91)

Defining the “YKP rapidity” corresponding to β _YK by

$$\displaystyle \begin{aligned} Y_{\text{YKP}} = \frac{1}{2} \: \ln \left( \frac{1+ \beta_{\mathrm{YK}}}{1- \beta_{\text{YK}}} \right) \: + y_{\mathrm{cm}} {} \end{aligned} $$

(7.92)

leads to the results in Fig. 7.68, indicating a strong correlation of the collective longitudinal source rapidity Y _YKP with the position of the pion pair in rapidity space.

Fig. 7.68

Emitting source rapidity (Y _YKP) as a function of pion pair rapidity (Y _ππ). From π ⁻pair correlation analysis in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV [90], and in central Au+Au collisions at $\sqrt {s}=200$ GeV [294]

We are interested in a possible non-monotonous $\sqrt {s}$ dependence of freeze-out parameters such as V _f because of recent predictions of the relativistic hydrodynamic model that a QCD critical point should act as an attractor of the isentropic expansion trajectories in the [T, μ _B] plane [101, 296]. Figure 7.69 shows such trajectories characterized by the ratio of entropy to net baryon number, S∕n _B, which is conserved in each hydro-fluid cell throughout the expansion. Note that the S∕n _B ratio is determined from the EOS during the primordial initialization stage in the partonic phase; the relationship between S∕n _B and $\sqrt {s}$ is thus not affected by the presence or absence of a critical end point (CEP) at T = T _c which, however, drastically influences the trajectory at later times as is obvious from comparing the left and right panels, the latter obtained with a first order phase transition at all μ _B but no CEP. In this case, the S∕n _B = const. trajectories in the partonic phase all point to the origin in the [T, μ _q] plane because $\mu _{\mathrm {q}}/T \propto \ln (S/n_{\mathrm {B}})$ in an ideal parton gas; whereas they point oppositely below T = T _c because $T^{3/2}/\varrho \propto \ln (S/n_{\mathrm {B}})$ in a hadron gas. This organization is dramatically upset for the cases S∕n = 100, 50, and 33 by the assumption of a CEP, tentatively placed here at T = 155 MeV, μ _B = 368 MeV.

Fig. 7.69

(Left) Influence of a critical point on hydrodynamic model isentropic expansion trajectories characterized by various values of entropy to net baryon number s∕n _B. (Right) The same trajectories without a critical point but a first order transition all along the phase boundary [296]

A first conclusion from this model is that it should not be essential to fine-tune $\sqrt {s}$ to make the system pass near the CEP because the attractor character would dominate over a substantial domain, e.g. at hadro-chemical freeze-out conditions 250 ≤ μ _B ≤ 500 MeV in the example of Fig. 7.69. Please note that hadro-chemical freeze-out is not treated correctly in this model, to occur at T _H which is 160 ≤ T _H ≤ 130 MeV from Figs. 7.1 and 7.33. The trajectories shown here belowT _H are thus not very realistic. The expected pattern could cause the “plateau” behavior of several observables at hadronic freeze-out over the range of SPS energies that corresponds to the above interval ofμ _B and T _H, e.g. $\left <m_{\mathrm {T}}\right >$ and T in Figs. 7.21 and 7.22, elliptic flow v ₂ at mid-rapidity in Fig. 7.36, and coherent hadronic freeze-out volume V _f from HBT in Fig. 7.67.

A consistent search for critical point effects implies, at first, a correct treatment of the hadronic expansion phase in hydro-models as above [101, 296], properly distinguishing chemical composition freeze-out, and eventual “thermal” freeze-out at hadronic decoupling. From such a model predictions for the $\sqrt {s}$ or S∕n _B systematics could be provided for the HBT source parametrization implied by Eqs. (7.84)–(7.86). I.e. the hydrodynamic model provides the correlator S(x, K) in cases with, and without a critical point which, as Fig. 7.69 shows, leads to considerable changes in the system trajectory in the domain near hadronization and onward to hadronic thermal freeze-out, at each given S∕n or $\sqrt {s}$. On the experimental side, this trajectory is documented by [T, μ _B] at hadronic freeze-out from grand canonical analysis [140] (Sect. 7.3) which also yields S∕n _B. Furthermore, as we shall show below, HBT in combination with the analysis of p _T or m _T spectra will describe the situation at thermal hadron freeze-out yielding T _f, β _T at the surface and the “true” transverse radius R _geom of the source, in addition to the coherence volume V _f illustrated in Fig. 7.67 (which also documents the present, insufficient data situation). Of course, we have to note that the lattice results concerning the critical point are not yet final [270], and neither is the hydrodynamic treatment [296] concerning the EOS in the vicinity of the CEP.

We turn to combined analysis of the two final processes of expansive evolution, formation of p _T spectra and decoupling to Bose-Einstein pair correlation, in order to show how the experimental information mentioned above can be gathered. At the level of “hydrodynamically inspired” analytic models for the emission function S(x, K) several approaches [106, 297] have established the connection, arising from radial flow, between hadronic m _T spectra and the K _T dependence of the HBT radii R _side, R _out and R _long, Eqs. (7.87), (7.92), which fall down steeply with increasing K _T [291,292,293,294]. A combined analysis lifts continuous ambiguities between the thermal freeze-out temperature T _f and the radial expansion velocity β _T (for which a radial profile β _T = (r∕R _side) β ₀ is assumed), that exist in the blast wave model derivation of both the p _T spectra, Eq. (7.25), and the K _T dependence of R _s.

This was first demonstrated in a NA49 study of pion correlation in central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV [90] that is shown in Fig. 7.70. The ambiguous anti-correlation of fit parameters T _f and $\beta ^2_{\mathrm {T}}$ can be somewhat constrained if several hadronic species are fit concurrently. This is obvious in Fig. 7.70 from the overlap of parametrization regions for negative hadron, and for deuterium m _T spectra. An orthogonal constraint on $\beta _{\mathrm {T}}^2/T_{\mathrm {f}}$ results from a blast wave model fit of the HBT K _T dependence of R _T ≈ R _side [298], employed here. We see that the three independent 1 σ fit domains pin down T _f and β _T rather sharply, to [115 MeV, 0.55]. A relativistic correction [297] leads to T _f = 105 MeV, β _T = 0.60. The $\sqrt {s}$ dependence of β _T at the freeze-out surface, from such an analysis [291, 297] is shown in Fig. 7.71. The data again exhibit a plateau at SPS energies, which remains to be understood [299]. In the light of the considerations above, the plateau might turn out to reflect a critical point focusing effect.

Fig. 7.70

Allowed regions of freeze-out temperature vs. radial expansion velocity for central Pb+Pb collisions at $\sqrt {s}=17.3$ GeV and mid-rapidity, combining negative hadron and deuterium spectral data analysis with BE π ⁻ correlation results on K _T dependence of R _⊥≈ R _s [90]

Fig. 7.71

The surface velocity (here denoted as ρ ₀) of radial expansion at decoupling in central Au+Au and Pb+Pb collisions vs. $\sqrt {s}$. From combined analysis of hadron p _T spectra and π ⁻pair correlation [291, 297]

7.8 Summary

We have seen that many physics observables in relativistic nucleus-nucleus collisions can, at RHIC energy $\sqrt {s}=200$ GeV, be related to the primordial dynamical phase, from initial QCD parton shower formation to local momentum space equilibration. The time interval is 0.35 to 0.65 fm/c. This domain can be investigated at RHIC due to the short interpenetration time, of 0.15 fm/c. From among the bulk hadron production signals, total and midrapidity charged particle rapidity densities, d N _ch∕d y, reflect the primordial parton saturation phenomenon [72]. It leads to an unexpectedly slow increase of multiplicity with fireball participant number N _part, and with $\sqrt {s}$. This observation signals the onset of nonperturbative QCD, a coherent shower multiplication by multigluon coherence [62, 65, 70, 71, 75]. It is expected to be even more dominant in LHC Pb+Pb collisions at 5.5 TeV. Furthermore, elliptic flow, a collective bulk hadron emission anisotropy, also originates from the primordial, nonisotropic spatial density profile of shower-produced partons [93, 96]. A hydrodynamic evolution sets in at t < 1 fm/c, implying the existence of a primordial equation of state (EOS) for partonic matter in local equilibrium. Moreover, the experimental elliptic flow data at RHIC are well described by “ideal fluid” hydrodynamics, i.e. by a very small shear viscosity η and a small mean free path λ [94, 95].

These observations indicate the existence of a (local) equilibrium state at very early times in the bulk parton matter stage of the dynamical evolution. This quark-gluon plasma (QGP) state of nonperturbative QCD was predicted by QCD lattice theory [11]. In Au+Au collisions at RHIC energy this state appears to be realized under the following conditions [61].

The energy density 𝜖 amounts to 6–15 GeV/fm³, far above the parton-hadron QCD confinement region at 𝜖 = 1 GeV/fm³, and at about 55 times the density of nuclear ground state matter, ρ ₀ = 0.14 GeV/fm³. Translating to macroscopic units we are dealing with a matter density of about 1.3 ⋅ 10¹⁹ kg/m³, the density prevailing in the picosecond era of the cosmological evolution. The corresponding temperature amounts to T = 300–330 MeV (about 3.6 ⋅ 10¹² K), far above the “Hagedorn limit” [38] for the hadronic phase (T _H = 165 MeV). From an analysis of the production ratios of the various hadronic species (from pions to Omega hyperons) arising from this primordial partonic state at hadronization, the statistical hadronization model (SHM) determines its baryo-chemical potential [108], μ _B = 20 MeV at RHIC energy. This value indicates that one is already close to the near-zero net baryon number conditions, μ _B ≈ 0, prevailing in the corresponding big bang evolution, where the density of particles exceeds that of antiparticles by a fraction of about 10⁻⁹ only.

Overall we thus obtain entries in the QCD phase diagram of Fig. 7.1. RHIC creates a parton plasma at about T = 300 MeV and μ _B = 20 MeV. It turns out to behave like an ideal fluid and features an extremely short mean free path λ, thus inviting a description by relativistic hydrodynamics. The small shear viscosity η (or the small viscosity to entropy ratio η∕s) are highlighted by the striking observation that even the fluctuations of primordial parton density in individual, single events, are preserved in the single event variation of elliptic flow [267, 268]. Moreover, the observed scaling of elliptic flow with hadron valence quark number [94]—and thus not with hadronic mass as in radial flow [103]—confirms the implied origin of the elliptic flow signal from the partonic phase.

At the LHC the phase of early QCD plasma formation is expected to shift to yet higher energy density, in the vicinity of T = 600 MeV and μ _B = 5 MeV. One is thus getting nearer to the domain of QCD asymptotic freedom, and might expect a falloff of the partonic cross section which is extremely high at RHIC [61], as reflected by the small η∕s and λ values.

The observed features of the QCD plasma produced at RHIC energy have invited the terminology of a “strongly coupled” quark-gluon plasma (sQGP [165]). Further evidence for the strongly coupled, non perturbative nature of the primordial partonic state stems from the various observed, strong in-medium attenuation effects on initially produced high p _T partons. In Au+Au collisions at $\sqrt {s}=200$ GeV this high medium opacity leads to a universal quenching of the high p _T hadron yield [175] including, most remarkably, heavy charm quark propagation to D mesons [175, 178]. We have shown in Sect. 7.5 that the interior of the collisional fireball at midrapidity is almost “black” at t < 1 fm/c. This is also reflected in a strong suppression of the back-to-back correlation of hadrons from primordially produced di-jets [207, 208], and in a similarly strong suppression of the J∕ Ψ yield [237] which we have shown in Sect. 7.6 to be ascribed to an in-medium dissolution of the primordially produced $c \bar {c}$ pairs [41] at T about 300 MeV.

The underlying high medium opacity can be formally expressed [188, 193, 195] by an effective parton transport coefficient $\hat {q}$ (Eqs. (7.58) and (7.62)) which quantifies the medium induced transverse momentum squared per unit mean free path λ. The value of $\hat {q}$ derived from analysis of the various attenuation phenomena turns out to be almost an order of magnitude higher than what was expected from former, perturbative QCD based models [196]. Analogously, η∕s has turned out to be much smaller than the previous perturbative QCD expectation [92]. The two quantities may be related [300] via the heuristic expression

$$\displaystyle \begin{aligned} \frac{\eta}{s} \approx 3.75 \ C \ \frac{T^{3}}{\hat{q}} {} \end{aligned} $$

(7.93)

with C a to be determined constant; C = 1∕3 from [300]. This relation shows that a larger value of $\hat {q}$ implies a small value for the ratio η∕s. The latter has a lower bound by the general quantum gauge field theory limit η∕s ≥ (4π)⁻¹ [171], a value not too far from the estimate η∕s = 0.09 ± 0.02 derived from relativistic hydrodynamics applied to elliptic flow v ₂ [94, 170]. As a consequence, $\hat {q}$ cannot grow beyond a certain upper bound that should be established at LHC energy.

These considerations are an example of the recent intense theoretical search for alternative methods of real-time strong coupling calculations, complementary to lattice QCD. In this regime, lattice QCD has to date been the prime non-perturbative calculational tool. However, understanding collective flow, jet quenching and primordial photon radiation requires real time dynamics, on which lattice QCD information is at present both scarce and indirect. Complementary methods for real-time strong coupling calculations at high temperature are therefore being explored. For a class of non-abelian thermal gauge field theories, the conjecture of a correspondence between anti-de Sitter space-time theory and conformal field theory (the so-called AdS/CFT conjecture) has been shown [301] to present such an alternative. It maps nonperturbative problems at strong coupling onto calculable problems of classical gravity in a five-dimensional anti-de Sitter (ADS₅) black hole space-time theory [302]. In fact, this formalism has been recently applied [212] in a calculation of the transport coefficient $\hat {q}$ that governs in-medium jet attenuation, resulting in an effective, expansion time averaged $\hat {q}_{\text{eff}} = 5$ GeV²/fm at T = 300 MeV corresponding to top RHIC energy, rather close to the experimental estimates (c.f. Figs. 7.41 and 7.48).

Thus, it does not seem to be too far-fetched to imagine [301] that the quark-gluon plasma of QCD, as explored at RHIC, and soon at the LHC (and theoretically in lattice QCD), and the thermal plasma of certain supersymmetric conformal gauge field theories (for example N = 4 “Super-Yang-Mills” (SYM) theory as employed in [212, 301]) share certain fundamental common properties.

The focus on early time in the dynamical evolution of matter in nucleus-nucleus collisions is specific to RHIC energy as the initial interpenetration period of two Lorentz contracted mass 200 nuclei amounts to 0.15 fm/c only. The subsequent evolution is thus reflected in a multitude of observables. It is, at first, described as a one-dimensional Hubble expansion [61], setting the stage for the emergence of the medium specific quantities addressed above (gluon saturation, direct photon production, hydrodynamic elliptic flow, jet quenching and J∕ Ψ suppression). These observables tend to settle toward their eventually observed patterns at t ≤ 1.0–1.5 fm/c, owing to the fact that they are most prominently determined under primordial conditions of high temperature and density. For example, photon production reflects T ⁴, and the transport coefficient $\hat {q}$ falls with T ³ [212].

On the contrary, at the energy of former studies at the CERN SPS, $6 \le \sqrt {s} \le 20$ GeV, such early times stay essentially unresolved as the initial interpenetration takes upward of 1.5 fm/c. A fireball system in local (or global) equilibrium thus develops toward t = 3 fm/c, at T about 220 MeV, closer to the onset of hadronization [85, 86]. Also the baryo-chemical potential is much higher than in RHIC collisions, 250 ≤ μ _B ≤ 450 MeV. However, we thus gain insight into the QCD physics of the hadronization, and high μ _B domain of the phase diagram sketched in Fig. 7.1, in the vicinity of the conjectured parton-hadron coexistence line of QCD.

For reference of such data, e.g. statistical species equilibrium (Sect. 7.3), dilepton studies of light vector meson “melting” at the phase boundary (Sect. 7.6.3), and hadronic event-by-event fluctuations (Sects. 7.7.2 and 7.7.3), to theoretical QCD predictions, a recent progress of lattice QCD [8,9,10] is of foremost importance. The technical limitation of lattice QCD to the singular case of vanishing chemical potential, μ _B = 0 (which arises from the Fermion determinant in the lattice formulation of the grand canonical partition function), has been overcome recently. Three different approaches have been outlined, the respective inherent approximation schemes touching upon the limits of both the mathematical and conceptual framework of lattice theory, and of present day computation power even with multi-teraflop machines. First results comprise the prediction of the parton-hadron phase boundary line, which interpolates between the well studied limits of the crossover-region at μ _B → 0, T ≥ T _c and the high net baryon density, low T region for which a first order character of the phase transition has been predicted by chiral QCD models [15]. We have illustrated this line in Fig. 7.1, and we have shown in Sect. 7.3 that hadronic freeze-out occurs at, or near this line at $\sqrt {s} \ge 17.3$ GeV (top SPS energy). The coexistence line includes an intermediate (T, μ _B) domain featuring a critical point of QCD at which the first order line at higher μ _B terminates, in a critical domain of (T, μ _B) in which the transition is of second order. One thus expects the nature of the confining hadronization transition—an open QCD question—to change from a crossover to a second order, and onward to a first order characteristics in a relatively small interval of μ _B that is accessible to nuclear collision dynamics at the relatively modest $\sqrt {s}$ of about 5 to 15 GeV. This domain has as of yet only received a first experimental glance, but the top AGS and low SPS energy experiments exhibit phenomena that can be connected to the occurrence of a critical point and/or a first order phase transition, notably the “SPS plateau” in $\left < m_{\mathrm {T}} \right >$, the non-monotonous K ⁺∕π ⁺ excitation function, and the eventwise fluctuations of this ratio (Sects. 7.2.6, 7.3, 7.7.2 and 7.7.3). A renewed effort is underway at RHIC, at the CERN SPS and at the future GSI FAIR facility to study hadronization, in-medium meson modification induced by the onset of QCD chiral restoration, as well as critical fluctuations and flow, in the low $\sqrt {s}$ domain.

7.9 Postscript

Reinhard Stock

7.9.1 Progress of the Field

Returning, after a decade, to the topic of “Relativistic Nucleus-Nucleus Collisions and the QCD Phase Diagram”, one is struck by the impressive progress that has transported many of the crucial themes, and physics observables, from initial, qualitative consideration to oftentimes quantitative comprehension. We shall briefly revisit some of these topics below, sketching the present state of the art, and mentioning some completely new developments (such as the study of light system collisions and, more spectacularly, the possible advent of Equation of State(EOS) information from neutron star mergers). This will, however, not be a real review but merely a narrative of recent progress.

The development of the field took a decisive turn by the startup of the CERN LHC collider which did not only move the energy frontier up to truly asymptotic values, 2.76 and 5.02 TeV per projectile nucleon pair in Pb + Pb collisions, but also introduced a completely new generation of nuclear collision experiments, offering an extended reach of physics observables and, moreover, a vastly increased event statistics capability ranging upward well into the 10⁹ domain. On the other hand, the “blockbuster” innovations from the late RHIC period, minimally viscous hydrodynamics with specific viscosity η∕s tantalizing close to the fundamental field theoretical limit (establishing the QGP as a near-ideal liquid), transport coefficients of the QGP from in-medium-jet quenching, statistical production of charmonia and the impression that charmed quarks are also thermalized in the deconfined QCD phase, the saturation of the QCD hadronization temperature near 160 MeV, just to mention the highlights, have remained the cornerstones of LHC physics to a large degree. This holds, also, for the notoriously evasive gluon saturation and Colour Glass Condensate physics, and to the inconclusive critical point searches. In retrospect, one may state that one very central and important element of the RHIC progress (handed on to the LHC physics) consisted of a clear separation of the collisional initialization time period (the first fm/c interval) from the ensuing hydrodynamical evolution and its in-medium effects. This provided for a much clearer relationship between data and theory: it is the simple feature that projectile-target interpenetration which took several fm/c at SPS energies is now shrunk to subfractions of a fm/c thus providing for a sharp, global synchronization of the successive eras of collisional dynamics: initialization, flow expansion, hadronization, final hadron/resonance “afterburning”. This is essential as one wants to tie the formation of the physics observables to a specific stage of the dynamical evolution, thus making them clearcut diagnostic tools.

One last thing. Neither RHIC nor the LHC experiments were built to explore phenomena typical of a large baryochemical potential, such as the critical point of QCD or the existence of a first order phase transition toward yet lower energies and, quite generally, the QCD phase diagram at high μ _B. However, at second thought a vigorous development at RHIC, the Beam Energy Scan(BES) program, as well as a re-vitalization of SPS experiments(the NA61/Shine experiment), and a concurrent brilliant extension of lattice QCD technique concerning (“critical”) fluctuation observables, were undertaken. Also, the low energy, high μ _B domain will come under renewed focus with new facilities, FAIR at GSI Darmstadt and NICA at JINR Dubna, both under construction.

In the following we will present brief sketches of the recent and concurrent work, theoretical and experimental, concerning a couple of (subjectively selected) observables: reaction dynamics decomposed into 4 characteristic, separate stages, initialization, hydrodynamic expansion, hadronization and final hadron/resonance “gas” expansion. We shall focus on the two characteristic parameters of the QCD plasma medium, the specific viscosity η∕s and the transport coefficient $\hat {q}$, as revealed by anisotropic flow and hadron/jet suppression, respectively. Then we turn to charmonium and bottonium suppression in the QCD medium, paying special attention to charmed meson statistical equilibrium hadronization. This leads us to hadronization and the information we have on the QCD phase diagram. These topics are all in full development since RHIC’s first decade of operation, and have been introduced in the preceding review article. Then we turn to a couple of more recent topics, e.g. small systems analysis, formation of light nuclei and antinuclei, critical point searches and the possible role of (now observable) neutron star mergers to unravel the EOS of cold hadronic matter.

7.9.2 Reaction Dynamics

Whereas, at the SPS energies, a central Pb + Pb collision featured some fraction of the collisional system already expanding toward hadronization at the time where the last participant nucleons just experienced their first collisions, the various evolutional stages are clearly separated from top RHIC energy onward. With Lorentz contraction factors in the hundreds to thousands domain, the primordial collisional system longitudinal size is less than a nucleon radius such that all primordial interactions occur “at once” so that after about 0.5 fm/c the initialization processes can be expected to settle down toward local equilibrium. This creates a primordial fireball that still features a highly clumpy energy density distribution. This distribution fluctuates from event to event due to a number of influences stemming from remaining impact parameter fluctuation, instantaneous density fluctuations within the average projectile-target Woods Saxon nucleon position/density profile (which are thus getting “photographed”), and by the presence or absence of colour saturation processes [303]. The latter can go along with the formation of a Colour Glass Condensate State [304] which decays to a parton system at the end of the initialization period, thus creating a particular topology of the primordial energy density distribution [305]. A model calculation of a zero impact parameter Au + Au collision transverse energy density distribution was already shown in Fig. 7.60, exhibiting pronounced clumpiness. This distribution is then, approximately, translated into the energy-momentum tensor that starts the next stage: hydrodynamic expansion. The most remarkable feature of this evolution (see below) is the occurrence of a nearly ideal hydro-flow dynamics which approximatively preserves information, the better the lower dissipative processes like shear viscosity turn out to be. Thus, most remarkably, the eventwise fluctuating primordial fireball profile becomes measurable after flow decoupling, modulo the strength of shear viscosity. Two of the objects of desire in this physics [306]!

The hydrodynamic evolution stage is thus, theoretically, well separable from the initialization period. The transition is, in itself, of course a matter of theoretical model building. We mention here, in particular, investigations of the AdS/CFT correspondence method [307] with respect to primordial equilibration [308]. Collective flow then transports the density distribution toward decoupling; this stage is analyzed under the general idea to follow the Fourier components 𝜖 _n of the primordial energy density distribution eccentricity as they get delivered to observation in the form of spatial flow anisotropics quantified [309] by their Fourier harmonics decomposition coefficients v _n(see ref. [310] and bibliography therein). Strictly speaking, the hydro-phase does not directly “deliver” the observables of viscous, anisotropic flow to observation. This phase ends at hadronization because the mean free path in the ensuing hadron-resonance(HR) expansion stage is too long for hydrodynamics to apply. One thus introduces a transition from hydro to HR gas by means of a hadronization model that translates hydro matter flow into hadron-resonance propagation (by the Cooper-Frye formalism [311]). The latter is then described by a hadron transport model acting as an “afterburner” [312, 313]. Such so-called hybrid models thus consist of three stages that incorporate stage specific dynamical models for initialization, hydro flow and hadron-resonance afterburning. This allows for a very wide variety of theoretical choices concerning the overall dynamics. Add to this that the experimental data from RHIC and LHC can be analyzed with various techniques, delivering the flow coefficients v _n(reaction plane method, cumulant method etc.). Thus an almost excessive wealth of data to model comparisons have been undertaken, with the highest focus on elliptical flow v ₂. Data exist for up to v ₆. In general v ₁—directed flow—and v ₂ are predominantly related to impact geometry variations of mass 200 collisions, creating anisotropic primordial energy density gradients. Whereas v ₃, in particular, appears to be more dependent on the primordial energy density profile and its even by event fluctuations, potentially related to Colour Glass Condensate(CGC) formation [314]. Very briefly summarizing the results one observes an anticorrelation between the initialization-, and the hydro flow-effects. The specific shear viscosity η∕s (that quantifies the speed with which the system approaches equilibrium) is tantalizingly close to the Kovtun, Son and Stariets [315] minimum of 1∕4π, throughout, but its deduced value at RHIC goes up with changing the initialization model from a “trivial” Glauber trajectory choice, to a CGC model, as is illustrated in Fig. 7.72 with RHIC STAR data [314] for v ₂ vs. theory [315]. Employing the Glauber initialization one deduces η∕s to be near 0.08 (the KSS limit) whereas the CGC model requires twice the shear velocity, about 0.16. The Glauber initial fireball is wider, spatially, than the one from the CGC model. That ambiguity has not finally been settled yet, it persists at the LHC, where the specific viscosity is slightly larger. The overall present result, within the CGC type of hybrid dynamical models, is given by Eskola and coworkers [316] and illustrated in Fig. 7.73. Similar results for η∕s have been given by other theory groups [313, 317]. In summary, an unambiguous conclusion about the QGP state as a near ideal liquid has been arrived at, whereas the existence of the CGC still remains to be finally established.

Fig. 7.72

STAR v ₂ data [314] confronted with viscous hydrodynamics [315] for various choices of η∕s, employing a Glauber- and a Colour Glass type initialization

Fig. 7.73

Energy dependence of η∕s from a simultaneous fit of RHIC and LHC data [316], with CGC initialization

7.9.3 Energy Loss in a QCD Medium: Hadron Suppression and Jet Quenching

The hydrodynamic model of the plasma evolution employs quantities that could be derived from QCD, for example the equation of state and the specific shear viscosity η∕s. A different aspect of the QGP is seen by an individual hard parton, or a jet, traversing it. In general, the overall medium effect will be energy loss and momentum broadening, as well as a re-appearance of the lost energy in the form of soft emission. A major obstacle in the interpretation of single parton(seen as hard hadrons) and jet attenuation is the medium expansion, i.e. one needs, not a hydrodynamic but a genuinely microscopic QCD transport model. Then the key ingredient in a theoretical description will be the parton transport parameter $\hat {q}$ that we introduced in Sects. 7.5.2 and 7.5.3. We recall that it represents the average transverse momentum broadening square per unit pathlength, $\langle p_{T}^{2} \rangle / \lambda$ (cf. [359,360,361,362, 366]). It is proportional to the local gluon number density. Recall further that the average in-medium energy loss is proportional to $\hat {q}$ [363]. This parameter can be systematically deduced from identified hadron p _T spectra in A + A collisions as compared to the same spectra in minimum bias p + p at similar energy, resulting in the nuclear modification factor R _AA as defined in Sect. 7.5.1. For jets the standard method is to estimate the jet energy loss by comparing the leading hadron (or fully reconstructed jet) energy on the trigger side with that of the away-side jet, where geometry has made sure that the trajectory traversed the QGP medium. Note, by the way, that $\hat {q}$ is inversely proportional to η∕s from Eq. (7.93) (from old article!). Thus if the latter is in a sense “near-minimal” the transport coefficient has to be near-maximal. So the medium opaqueness might completely wipe out the jet at lower energies, as was indeed observed at RHIC (see Figs. 7.50 and 7.53): the black interior situation. At the LHC jet energies are always sufficient to observe both jet sides. We illustrate that in Fig. 7.74 [318] where we see very significant suppression in the “low” energy domain of recent LHC Pb + Pb data, gradually weakening toward high p _T. This indicates that the energy loss is not growing in proportion to p _T. Corresponding results for the p + Pb jet production at the LHC indicates essentially zero medium effect, asserting that the suppression in Pb + Pb is indeed a final state, QGP effect. We mentioned above that all data concerning heavy flavour charm quark attenuation point to a behaviour similar to that of the light quarks. This is illustrated in Fig. 7.75 by ALICE data [319] for D meson production in p + Pb and Pb + Pb, central Pb + Pb collisions again showing drastic suppression whereas this is absent in the p + Pb collision. We should also mention here that the charmed hadrons follow the flow v _n patterns observed for light quark hadrons. In the end, all A + A data, both about the shear viscosity, near minimal, and the transport coefficient, have been shown to be semi-quantitatively consistent [320]. Figure 7.76 shows the result of current state of the art theory; quite remarkably, the theory groups have followed the example of the experimentalists, forming collaborations. Here we show the transport coefficient results from the JET Collaboration [320], extracted from fits to the combined data from RHIC and LHC, as of 2014. Indeed, the transport coefficient falls with temperature, consistent with the inversely proportional specific shear velocity rising with T. Note that the temperature scale reflects the energy density in the center of the fireball at an initial time of 0.6 fm/c, that we have ascribed above to the end of the primordial initialization period. This would be the medium in which the hard partons born by perturbative QCD interactions start embedding. The results of many theory collaborations are indicated in this Figure (see ref. [320]). The JET collaboration employs perturbative QCD technique to generate the jets in the primordial A + A environment, then follows them through the co-travelling non-perturbative QCD plasma medium. This situation is characteristic of all “hard probes” studies: one has to combine the short range pQCD scale with the long range scale inherent in the structure(s) of the plasma QCD medium: the leading parton does not interact with a free gas of partons! The diagnostic of this state is the goal of all had probes physics. The present estimate [320] of the transport coefficient amounts to about 1.5 GeV²∕fm for a 10 GeV quark jet. The lost energy gets radiated by soft gluon emission from the plasma and is indeed recovered experimentally in hadrons populating the vicinity of the jet cone. The question of the elementary degrees of freedom in a high T QCD plasma is coming within reach by such studies.

Fig. 7.74

Nuclear Modification Factors for jet production, obtained by the ALICE, CMS and ATLAS LHC collaborations, for p + Pb and Pb + Pb collisions[318]

Fig. 7.75

R _AA factors for D meson production in p + Pb and Pb + Pb, by ALICE at LHC [319]

Fig. 7.76

Temperature dependence of the jet transport coefficient $\hat {q}/T^{3}$, extracted with different approaches for jet quenching at an initial jet energy of 10 GeV, in central A+A collisions (see ref. [320])

7.9.4 Charmonium

The J∕ Ψ signal entered relativistic heavy ion physics as the “Holy Grail” observable of QGP formation by the work of Matsui and Satz [321], at the time the CERN SPS A + A program took shape, in the late 1980s. From among all observables predicted then to provide evidence of QCD deconfinement and QGP formation, the proposed in-medium colour Debye-screening mechanism preventing the primordially produced $c\bar {c}$ pair to hadronize as a J∕ Ψ hidden charm meson was presenting a direct link between deconfined partons and the suppressed cross section of observed J∕ Ψ, which was relatively well known from elementary p + p and e ⁺ + e ⁻ collisions. We have reported in Sect. 7.6.1 on the success of the charmonium suppression idea at the SPS (Fig. 7.54) and at RHIC (Fig. 7.55). However, we recall that it was predicted early on that if free charm and anticharm quarks were thermalized in the plasma medium (as has been verified meanwhile) they would hadronize statistically forming open charm mesons and charmonia [322] in relative hadro-chemical equilibrium, along with all other hadrons, albeit with a separate fugacity factor for c and $\bar {c}$ because these stem from the early hard collision phase unlike the majority of the lighter quarks [323]. We note that this mechanism is oftentimes called recombination, erroneously so as the thermal charm quarks do not really stem from Debey-screened J∕ Ψ breakup which covers a mere 1% fraction of the total primordial charm-anticharm production. The statistical $c\bar {c}$ hadronisation mechanism and its traces in RHIC data were soon to be fully substantiated [324]. At LHC energy we expect a significantly higher number density of thermalized c and $\bar {c}$ quarks as the system enters hadronization and, hence, a higher fraction of chemical equilibrium charmonia (for a recent review see ref [325]). Indeed, Fig. 7.77 (from [325]) shows that the R _AA ratios for J∕ Ψ drop down far more steeply with midrapidity multiplicity (centrality) at RHIC than at the LHC where, indeed, not much of the low energy charmonium suppression remains visible, being overshadowed here by the statistical production. We might remark that nobody nowadays insists on a proof of deconfinement anymore (as was the case in 1986) and, furthermore, that the universality of statistical hadron production in A + A collisions, of which we see evidence here, is in itself a strong manifestation of deconfinement. To this topic we turn our attention next, but remark, in passing, that the suppression theme is now turning over to the bottonomium production at the LHC [326], visible there because of the much lower thermal bottom quark density.

Fig. 7.77

Multiplicity(centrality) dependence of the Nuclear Modification Factor for J∕ Ψ production at mid-rapidity at top RHIC, and at LHC energy [325]

7.9.5 Hadronization and the QCD Phase Diagram

This chapter will have two main topics, first the analysis of hadron production multiplicities with the Statistical Hadronization Model (SHM) that incorporates the canonical or grandcanonical partition functions of a hadron-resonance gas (HRG) model. This will be an update on Sect. 7.3. Second, however, we turn to new developments of lattice QCD theory, extension to finite baryochemical potential and determination of the hadronization parameters T vs. μ _B from, first, a determination of the overlap between Lattice QCD and the HRG model [327], to reveal the “hadronization point” and, second, from fitting new data concerning fluctuation of conserved charges to higher order Lattice susceptibilities [328]. Some remarks are also necessary with regard to the Lattice conclusion that the parton to hadron phase transition is “merely” a cross-over at small μ _B, top RHIC and LHC energy.

We have shown in Sect. 7.3.4 that, ideally, the Statistical Hadronization Model(SHM) freeze-out curve should reveal the QCD parton-hadron phase transformation line in the (T, μ _B) plane, i.e. the most prominent feature of the QCD phase diagram. This follows from the assumption that inelastic reactions (except resonance decays) among hadrons cease directly at the instant of hadronization: chemical hadron freeze-out determines the hadronization “point” corresponding to the chosen A + A collision energy. Add, for correctness: as long as freeze-out occurs from the QCD hadronization transition, i.e. from a QGP. About freeze-out from hot, dense hadronic matter in expansion, we do not yet know the final interpretation of the hadronic multiplicities. Now, the above ideal picture, absence of final state effects from the afterburning phase, may require certain corrections. It has been shown [329] that, on the one hand, the bulk hadrons from a relativistic A + A collision (i.e. pions and kaons that carry about 95% of the total cm energy output at LHC energy) do indeed pass the afterburner stage essentially unchanged. At the relatively low SPS energies, this applies also to protons and Lambdas. Whereas the antibaryon yields get reduced, away from chemical equilibrium, by annihilation processes that occur throughout the hadron/resonance expansion phase. At top RHIC and LHC energies, baryons and antibaryons are similarly affected, with the exception of the Omega hyperons which suffer little annihilation. These afterburner effects were quantified [330] by the microscopic transport model UrQMD [312] which is employed in many of the current multi-stage “hybrid” models [313, 316] for the afterburner stage. The thus obtained modification factors for each species were applied to the grand canonical partition functions of the SHM [330]. We show the results in Fig. 7.78, which gives (T, μ _B) points for AGS, SPS and LHC energies. The overall result of the annihilation corrections is seen to be an upward shift of the hadronization curve(see also [331]), above the curve resulting from the uncorrected SHM procedure which agrees with other SHM work [332]. The modified approach also explains the so-called “nonthermal proton to pion ratio puzzle” at the LHC [332], much discussed but simply resulting, in this model, from proton annihilation going to pions, thus decreasing the p∕π ratio; of course a non-thermal effect [333]. The pseudo-critical temperature at μ _B=0 turns out to be 164 ± 5 MeV, as compared to about 155 MeV in the standard approach. This new development is still vigorously contested by the ALICE community [325, 332]; it appears highly desirable that groups employing a different afterburner model turn their attention to the final state effects.

Fig. 7.78

Freeze-out points in the (T, μ _B) plane extracted from hadron multiplicity data at LHC, SPS and AGS energies, obtained with the standard Statistical Hadronization Model, and with the SHM corrected for baryon-antibaryon annihilation during the afterburner phase [330]

The reader will have noticed that entries from RHIC are missing in Fig. 7.78. This is the result of another tension in the community. By far the most comprehensive set of hadron multiplicity data stems from the STAR experiment at RHIC [334] which, up until now, has published baryon/antibaryon multiplicities without correction for feeddown from weak hyperon decays which are misidentified as primary particles (this omission is now disposed of, for subsequent data taking, by the new STAR vertex tracking detector [335]). Accidentally, the extra particles from feeddown do closely compensate for the losses by annihilation, and a picture of perfect equilibrium thus emerges from SHM analysis [334]. Then, apparently, there arises no p∕π puzzle at top RHIC energy, the two missing corrections cancelling. We are at μ _B about 20 MeV, very close to the value of about 1 MeV encountered at LHC. A kink in the phase diagram? Clearly an inconsistency. In ALICE at the LHC, the primary vertex is very precisely reconstructed, eliminating secondary decays, and NA49 at the SPS has employed a formidable correction simulation to determine the feeddown fractions, of order 50%. Once all this dust settles, one can still expect an interesting freeze-out curve [323], which should reflect influences of a critical point, perhaps even adjacent to a new, further form of QCD phase transition, from quarkyonic [337] to hadronic matter, that interpolates between the partonic and the hadronic phases at high μ _B [323]. This region in the QCD phase diagram will receive the necessary attention by NA61(SPS) and by the FAIR and NICA projects.

We turn to a second, very much elaborated source of information about the parton-hadron phase boundary, which was made possible by recent developments of Lattice QCD. In a way, this progress was a generalization of the attempt to extend Lattice QCD from μ _B=0 to finite baryochemical potential [336], by a Taylor expansion of the reduced thermodynamic pressure in terms its derivatives with respect to μq∕T :

$$\displaystyle \begin{aligned} {p\over T^4}={1\over{VT^3}}\ln{\mathcal{Z}}. \end{aligned} $$

(7.94)

(7.95)

where derivatives are taken at μ _q = 0. The derivatives of the reduced pressure, of order n on the r.h.side of equ. [304], with respect to a chemical potential, are called susceptibilities. In general, fluctuations of conserved quantum numbers are obtained as derivatives of the pressure to various chemical potentials μ _X∕T, where X stands for net baryon number B, charge Q, strangeness S or charm C (see [328, 337, 338] and references therein). Also one can formulate correlations of net charges X and Y by mixed susceptibilities [339] which contain derivatives jointly to μ _X and μ _Y. Now, all such susceptibilities could be obtained from recent Lattice calculations, up to order six, as well as from the Hadron Resonance Gas (HRG) model and, most significantly, some of them can be related to experimentally accessible quantities. For example, net baryon number fluctuations (one can approximate them by net proton number fluctuations) are expressed by properties of the event by event multiplicity distribution, e.g. mean (M _B), variance ($\sigma _B^2$), skewness (S _B) and kurtosis (κ _B):

$$\displaystyle \begin{aligned} \begin{array}{rcl} R_{12}^B(T,\mu_B)&\displaystyle \equiv&\displaystyle \frac{\chi_1^B(T,\mu_B)}{\chi_2^B(T,\mu_B)} \equiv \frac{M_B}{\sigma_B^2}\; , \\ R_{31}^B(T,\mu_B)&\displaystyle \equiv&\displaystyle \frac{\chi_3^B(T,\mu_B)}{\chi_1^B(T,\mu_B)} \equiv \frac{S_B\sigma_B^3}{M_B}\; , \\ R_{42}^B(T,\mu_B)&\displaystyle \equiv&\displaystyle \frac{\chi_4^B(T,\mu_B)}{\chi_2^B(T,\mu_B)} \equiv \kappa_B \sigma_B^2 \; . {} \end{array} \end{aligned} $$

(7.96)

where the n-th order susceptibilities $\chi _{n}^{B}$ are obtained from the corresponding partial derivatives of the Lattice or HRG pressure P(T, μ _X) with respect to the baryon chemical potential, and the mean, variance, skewness and curtosis from the data on net proton number fluctuations e.g. by the STAR Collaboration at a set of RHIC energies [340]. We cannot do justice to this very wide body of recent work here but merely present two typical results. Figure 7.79 illustrates the Lattice-HRG overlap analysis [341] technique showing the normalized pressure, energy density and entropy density as a function of temperature, at μ _B = 0. The HRG curves start seriously departing from the Lattice results above about 170 MeV. Recall that the parton-hadron-transition is a relatively broad cross-over at μ _B=0; so we would conclude that the crossover domain ends here. The center of the pseudo-critical region might thus be at about 160 MeV, at μ _B = 0; the authors also show the region center and width estimate from other analyses [337]: not really fully supported by the present analysis. The most recent results in the comparison of Lattice with the STAR kurtosis data are shown in Fig. 7.80 (taken from ref [338] which gives a comprehensive review of the topic). It shows the ratio of the two susceptibilities $\chi _{4}^B$ and $\chi _{2}^{B}$, equal to kurtosis times variance, vs. temperature, from various state of the art Lattice calculations, and a band about a freeze-out temperature of T = 153 MeV indicated by the data. We cannot exhaust the topic which is under vigorous development but wish to enumerate points of concern that are presently under investigation:

• 1. It is unclear whether various hadronization observables like hadron multiplicities and higher order multiplicity fluctuations should refer to an identical freeze-out temperature within the relatively broad pseudocritical temperature band. The latter might freeze out later (sequential freeze-out).

  Fig. 7.79

  

  The overlap between Lattice QCD and Hadron Resonance Gas(HRG) model calculations of the normalized pressure, energy density and entropy density, as a function of temperature [341]. It is seen that the results match over a relatively broad temperature domain, characteristic of a cross-over transition, and slightly different for the three quantities

  Fig. 7.80

  

  The ratio of the two susceptibilities $\chi _{4}^B$ and $\chi _{2}^{B}$, equal to kurtosis times variance, vs. temperature, from various state of the art Lattice calculations [338], and a band about a freeze-out temperature of T = 153 MeV indicated by the data

• 2. Net proton multiplicity is not a conserved quantity but taken here as a proxy for net baryon number: an approximation sensitive to the experimental energy and acceptance [342, 343].

• 3. Higher order fluctuations and their ratios receive sizeable contributions from the fluctuation, event by event, of the participant nucleon number [343].

• 4. Higher order fluctuations can be dampened in the course of the afterburner expansion [344].

• 5. The standard Hadron-Resonance Gas model employed in the Lattice-HRG overlap study may need amendments due to Van der Waals-Type hadron-hadron repulsion [345], or to high lying strange resonances that are not yet experimentally known [346].

Clearly, these questions need to be addressed before we can finally conclude on the QCD phase diagram and the parton-hadron phase boundary.

7.9.6 New Topics

7.9.6.1 Proton Induced Collisions

In defining the nuclear modification factor R _AA (Sect. 7.9.3) we have employed, in the denominator, the experimental minimum bias p + p momentum distribution at the same cm energy as the energy per participant nucleon pair of the A + A data forming the numerator. Thus, the p + p cross section is employed as a reference, to incorporate the “no QGP physics” situation that is captured in the Glauber model which describes the A + A collision as an superposition of independent, minimum bias nucleon-nucleon collisions occurring at the microscopic level. Of course this cannot be a realistic model but for the hard, partonic collisions occurring during the primordial interpenetration we may still employ it as a standard of comparison. Nevertheless it was tempting to check whether p + p collisions revealed any of the effects ascribed to the QGP medium in A + A collisions, such as grand canonical hadrochemical equilibrium at 160 MeV apparent temperature, collective hydrodynamic flow in its multifold Fourier harmonics phenomena, jet attenuation etc., thus making it useless as a “no new physics” standard reference. This experimental program occupied the first half of this decade, both at RHIC and LHC. Lacking space for detail, we briefly summarize the main results. Indeed, minimum bias p + p collisions turned out to be essentially free of the new physics: ok to employ them in R _AA. However, onset behaviour of grand canonical hadronization [347], of elliptic flow [348], and new modification patterns of jet production [349] were observed in high multiplicity selections of p + p data at LHC where the midrapidity charged particle density increases from about 8 in minimum bias mode, up to well beyond 20 in the ALICE study [347], with extremes ranging up to about 80. No surprise then: these are geometrically small but energy rich systems which lead to equilibrium conditions due to extreme density of degrees of freedom. Such that the bulk phenomena, advent of grandcanonical hadronization [347] and development of anisotropic hydro flow, exhibit onset patterns. Whereas the hard probes which depend on pathlength might well still stay unaffected of the medium. No big surprise, but initially the community was quite smitten by the surfacing of typical QGP signals in an elementary collision. A different, completely new aspect concerning jet production: the selection of extreme multiplicity density at midrapidity clearly represents a strong bias as to the primordial partonic collision generation, possibly selecting for changes in jet observables [349]. An interesting, unexplored aspect of jet production.

Along with p + p came a wave of p + Au∕Pb collision studies. Here we would expect that the projectile side of rapidity space shows essentially p + p properties whereas the heavy nucleus side shows, firstly, a strong dependence of impact parameter and participant nucleon number variation. Second, the resulting primordial fireballs should grow in proportion to N _part, leading to clear collective signals in the bulk production observables, emerging with increasing centrality (multiplicity), as was indeed observed [347, 350]. However, again the hard probes did not show significant attenuation as we have seen in Figs. 7.74 and 7.75 for LHC collisions [318, 319]. It is reassuring to confirm that extended path length in hot QGP matter is required in order to produce attenuation, whereas cold nuclear spectator matter has a very low transport parameter [320]. In general p + Pb collisions share the complicating feature, common to all light-on-heavy collisions, that the effective center of mass for soft production moves away from the corresponding p + p cm frame that controls hard processes, as N _part increases. At the LHC this shift goes up to two rapidity units for very central collisions, potentially causing more or less trivial effects in the attenuation of hard partons traversing the soft-produced QGP medium [351]. Also the effective midrapidity position for soft, bulk production is now outside the acceptance for ALICE.

7.9.6.2 Lambda Polarization and Fireball Vorticity

Huge global angular momenta are generated in non-central A + A collisions. In fact they get converted to the vorticity of a QGP [352] and get transmitted to particle polarization at the stage of hadron formation and particlization whence hadrons are emitted from the hypersurface of a hydrodynamically expanding fireball (51, 52). The global angular momentum can thus lead to the local polarization of hadrons. The polarization, in turn, can be measured by Λ and $\bar {\Lambda }$ hyperon weak decay into a proton and a pion which is “self-analyzing” since the proton is emitted preferentially along the direction of the Lambda spin in its rest frame. The global polarization (the net polarization of the local ones in an event which is aligned in the direction of the event plane, i.e. along the direction of the angular momentum of the plasma) of Λ and $\bar {\Lambda }$ has recently been measured by the RHIC STAR Collaboration [355] at collisional energies below 62.4 GeV. At higher energies, including LHC, the falling of the polarization with energy [355] still precludes measurement. The measurement determines the event average of $\sin {}( \Phi _{p} - \Psi _{RP})$, where Φ_p and Ψ_RP are the azimuthal angle of the proton momentum in the Lambda rest frame, and that of the reaction plane. Its orientation cannot be directly measured but is approximated by the event plane determined from the hadronic directed flow; this is accounted for by a reaction plane resolution factor [355]. Alternative methods have been proposed recently [356]. For an overview see ref. [357].

From the data one can estimate [353, 354] the local vorticity in the plasma, the result implying that the QCD matter created in such collisions is the most vortical fluid known as of yet. Moreover, this new observable can shed a new, independent light on the equilibrium properties encountered (or not) in the course of (relativistic hydro) expansion toward hadronization [358].

7.9.6.3 EOS from Neutron Star Mergers

The recent observation of gravitational waves from a neutron star merger has, in fact, been anticipated with regard to its possible sensitivity to the EOS of dense hadronic matter at low temperature and high baryochemical potential. This is a topic of nuclear collision research already since the early BEVALAC studies at LBL when it was realized that the EOS should be of importance, both, to the dynamics of supernova explosions and to the radial structure of neutron stars, also affecting their maximum mass with regard to black hole formation. The hope was to derive the EOS from the data concerning hydrodynamic directed sidewards expansion, and from Kaon production in A + A “compressive collisions” [359] at the low BEVALAC energies, in the GeV per nucleon energy range. One of the key problems arose from the fact that even at these energies the collisional fireball temperature ranges up to about 100 MeV whereas the above astrophysical phenomena require the EOS of cold, compressed matter [360]. The newly accessible Neutron star mergers promise to open up a window to the low T EOS [361], and to crucial transport parameters [362], once more experimental information becomes available, as can be expected.

7.9.6.4 Production of Light Nuclei in A + A Collisions

At RHIC and LHC, a large number of light nuclei and antinuclei have been measured [325, 363, 364], from deuterium to anti-alpha. This continues a tradition dating back to BEVALAC time [365] and SPS [366]. Dating back is also the controversy concerning model description or, alternatively stated, the lack of a comprehensive understanding [325, 364, 367]. The Statistical Hadronization Model(SHM) gives a very good description(hadro-chemical freeze-out) of the LHC yields [325], along with all other hadron multiplicities. The coalescence model [365, 367] addresses the end of the hadron/resonance expansion stage (kinetic freeze-out), whence the produced nucleons, spread out in phase space, overlap, to a certain degree, with the internal wave functions of the various clusters. There are difficulties in both views if one takes them literally. The clusters cannot have existed at 160 MeV, the hadronization temperature. On the other hand, the coalescence cannot proceed on-shell because of the cluster binding energies (that are ignored in the model). All this points to a deeper flaw in, either the models, or their conventional understanding. The role of quantum mechanics seems to be missing, as pointed out long ago by E. Remler [368]. Hadronization does not directly produce a decoherent, on-shell state, in A + A collisions. If hadronization occurs via the quantum mechanical decay of initially produced colour singlet clusters (see Sect. 5.3.3), then Fermis Golden Rule refers to the phase space weights AFTER decoherence. And, in fact, in the SHM partition functions we employ the set of in-vacuo free masses of the produced particles, also for the clusters, with apparent success. One might then speculate that the number densities and their ratios are fixed by the entropy at hadronization, but we have to wait until after the freeze-outs to have them decohere. This is a speculation, of course.