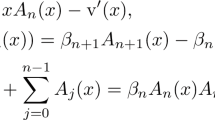Abstract
In this lecture we discuss properties of orthogonal polynomials for weights which are semiclassical perturbations of classical orthogonality weights. We use the moments, together with the connection between orthogonal polynomials and Painlevé equations to obtain explicit expressions for the recurrence coefficients of polynomials associated with a semiclassical Laguerre and a generalized Freud weight. We analyze the asymptotic behavior of generalized Freud polynomials in two different contexts. We show that unique, positive solutions of the nonlinear difference equation satisfied by the recurrence coefficients exist for all real values of the parameter involved in the semiclassical perturbation but that these solutions are very sensitive to the initial conditions. We prove properties of the zeros of semiclassical Laguerre and generalized Freud polynomials and determine the coefficients a n,n+j in the differential-difference equation
where P n(x) are the generalized Freud polynomials. Finally, we show that the only monic orthogonal polynomials \(\{P_n\}_{n=0}^{\infty }\) that satisfy
where π(x) is a polynomial of degree at most 4 and \(\mathcal {D}_{q}\) is the Askey–Wilson operator, are Askey–Wilson polynomials and their special or limiting cases, using this relation to derive bounds for the extreme zeros of Askey–Wilson polynomials.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
W.A. Al-Salam, T.S. Chihara, Another characterization of the classical orthogonal polynomials. SIAM J. Math. Anal. 3, 65–70 (1972)
S.M. Alsulami, P. Nevai, J. Szabados, W. Van Assche, A family of nonlinear difference equations: existence, uniqueness, and asymptotic behavior of positive solutions. J. Approx. Theory 193, 39–55 (2015)
A. Arceo, E.J. Huertas, F. Marcellán, On polynomials associated with an Uvarov modification of a quartic potential Freud-like weight. Appl. Math. Comput. 281, 102–120 (2016)
A.F. Beardon, The theorems of Stieltjes and Favard. Comput. Methods Funct. Theory 11, 247–262 (2011)
S. Bochner S, Über Sturm-Liouvillesche Polynomsysteme. Math. Z. 29(1), 730–736 (1929)
L. Boelen, W. Van Assche, Discrete Painlevé equations for recurrence relations of semiclassical Laguerre polynomials. Proc. Am. Math. Soc. 138, 1317–1331 (2011)
Y. Chen, M.V. Feigin, Painlevé IV and degenerate Gaussian Unitary Ensembles. J. Phys. A Math. Gen. 39, 12381–12393 (2006)
Y. Chen, M.E.H. Ismail, Ladder operators and differential equations for orthogonal polynomials. J. Phys. A 30, 7817–7829 (1997)
T.S. Chihara, An Introduction to Orthogonal Polynomials (Gordon and Breach, New York, 1978). Reprinted by Dover Publications (2011)
A.S. Clarke, B. Shizgal, On the generation of orthogonal polynomials using asymptotic methods for recurrence coefficients. J. Comput. Phys. 104, 140–149 (1993)
P.A. Clarkson, K. Jordaan, The relationship between semiclassical Laguerre polynomials and the fourth Painlevé equation. Constr. Approx. 39, 223–254 (2014)
P.A. Clarkson, K. Jordaan, Properties of generalized Freud polynomials. J. Approx. Theory 225, 148–175 (2018)
P.A. Clarkson, K. Jordaan, A. Kelil, A generalized Freud weight. Stud. Appl. Math. 136, 288–320 (2016)
S. Datta, J. Griffin, A characterization of some q-orthogonal polynomials. Ramanujan J. 12(3), 425–437 (2006)
K. Driver, K. Jordaan, Bounds for extreme zeros of some classical orthogonal polynomials. J. Approx. Theory 164, 1200–1204 (2012)
J. Favard, Sur les polynomes de Tchebicheff. C. R. Acad. Sci. Paris 200, 2052–2053 (1935)
G. Filipuk, W. Van Assche, L. Zhang, The recurrence coefficients of semiclassical Laguerre polynomials and the fourth Painlevé equation. J. Phys. A 45, 205201 (2012)
G. Freud, On the coefficients in the recursion formulae of orthogonal polynomials. Proc. R. Irish Acad. Sect. A 76, 1–6 (1976)
A.G. García, F. Marcellán, L. Salto, A distributional study of discrete classical orthogonal polynomials. J. Comput. Appl. Math. 57(1–2), 147–162 (1995)
W. Hahn, Über die Jacobischen Polynome und zwei verwandte Polynomklassen. Math. Z. 39(1), 634–638 (1935)
E. Hendriksen, H. van Rossum, Semi-classical orthogonal polynomials, in Polynômes Orthogonaux et Applications, ed. by C. Brezinski, A. Draux, A.P. Magnus, P. Maroni, A. Ronveaux. Lecture Notes in Mathematics, vol. 1171 (Springer, Berlin, 1985), pp. 354–361
M.E.H. Ismail, A generalization of a theorem of Bochner. J. Comput. Appl. Math. 159(2), 319–324 (2003)
M.E.H. Ismail, in Classical and Quantum Orthogonal Polynomials in One Variable. Encyclopedia of Mathematics and its Applications, vol. 98 (Cambridge University Press, Cambridge, 2005)
M.E.H. Ismail, X. Li, Bounds for extreme zeros of orthogonal polynomials. Proc. Am. Math. Soc. 115, 131–140 (1992)
J. Jost, Postmodern Aanalysis (Springer, Berlin, 2006)
T. Kasuga, R. Sakai, Orthonormal polynomials with generalized Freud-type weights. J. Approx. Theory 121, 13–53 (2003)
M. Kenfack Nangho, K. Jordaan, A characterization of Askey–Wilson polynomials. Proc. Am. Math. Soc. 147(6), 2465–2480 (2019)
M. Kenfack Nangho, K. Jordaan. Structure relations of classical orthogonal polynomials of the quadratic andq-quadratic variable. SIGMA, 14, 26 (2018)
R. Koekoek, P.A. Lesky, R.F. Swarttouw, in Hypergeometric Orthogonal Polynomials and Theirq-Analogues. Springer Monographs in Mathematics (Springer, Berlin, 2010)
J.S. Lew, D.A. Quarles, Nonnegative solutions of a nonlinear recurrence. J. Approx. Theory 38, 357–379 (1983)
F. Marcellán, R. Álvarez-Nodarse, On the “Favard theorem” and its extensions. J. Comput. Appl. Math. 127, 231–254 (2001)
I.P. Natanson, Konstruktive Funktionentheorie (Akademie-Verlag, Berlin, 1955)
P. Nevai, Géza Freud, orthogonal polynomials and Christoffel functions. A case study. J. Approx. Theory 48, 3–167 (1986)
F.W.J. Olver, D.W. Lozier, R.F. Boisvert, C.W. Clark (eds), DLMF Handbook of Mathematical Functions (Cambridge University Press, Cambridge, 2010)
J. Shohat, The Relation of the classical orthogonal polynomials to the polynomials of appell. Am. J. Math. 58, 453–464 (1936)
J. Shohat, Sur les polynômes orthogonaux généralises. C. R. Acad. Sci. Paris 207, 556–558 (1938)
M.H. Stone. Linear transformations in Hilbert space and their applications to analysis. AMS Colloquium Publications, vol. 15 (American Mathematical Society, Providence, 1932)
T.J. Stieltjes, Recherches sur les fractions continues. Ann. Fac. Sci. Toulouse Sci. Math. Sci. Phys. 8, J1–J122 (1894); A5–A47 (1895)
W. Van Assche, The impact of Stieltjes work on continued fractions and orthogonal polynomials, in Collected Papers, ed. by G. van Dijk (Springer, Berlin, 1993), pp. 5–37
L. Vinet, A. Zhedanov, Generalized Bochner theorem: characterization of the Askey–Wilson polynomials. J. Comput Appl. Math. 211(1), 45–56 (2008)
Z.T. Wen, R. Wong and S.X. Xu, Global asymptotics of orthogonal polynomials associated with a generalized Freud weight. Chin. Ann. Math. Ser. B, 39, 553–596 (2018)
A. Wintner, Spektraltheorie der unendlichen Matrizen (S. Hirzel, Leipzig, 1929)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Jordaan, K. (2020). Properties of Certain Classes of Semiclassical Orthogonal Polynomials. In: Foupouagnigni, M., Koepf, W. (eds) Orthogonal Polynomials. AIMSVSW 2018. Tutorials, Schools, and Workshops in the Mathematical Sciences . Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-36744-2_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-36744-2_18
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-36743-5
Online ISBN: 978-3-030-36744-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)