Iris Recognition by Learning Fragile Bits on Multi-patches using Monogenic Riesz Signals

Abstract

Unconstrained, at-a-distance iris recognition systems endure the problem of fragile bits. Existence of fragile bits in candidate iris results into low recognition rates. Proposed approach utilizes fragile-bit information for classification of iris bits as consistent or inconsistent. We divide the candidate iris into patches and propose monogenic signals of Riesz wavelets to learn fragile bits in each patch. We propose a new feature descriptor, Riesz signal based binary pattern (RSBP) to extract the features from these patches. Each patch is assigned with a weight pivoted on the fragile bits present in it. Dissimilarity score between the two irises is obtained by adopting weighted mean Euclidean distance (WMED). Experiments are conducted using both near infra red (NIR) and visible wavelength (VW) images, obtained from the benchmark databases IITD, MMU v-2, CASIA-IrisV4-Distance and UBIRIS v2. Results justify the applicability of proposed approach for iris recognition.

1 Introduction

Because of intricate textural pattern of the stroma in human iris, iris biometrics manifests low miss match rates compared to rest of the biometric traits [10]. Earlier works on iris biometrics deal with the iris images obtained under constrained scenario and have obtained promising results. However, when iris images are obtained from long stand-off distances under unconstrained imaging, acquired iris information will be very poor because of bad illumination and less cooperation by the subject and results into high intra-class variations [17]. Such degraded iris images are occluded by eye-lids, eye-lashes, eye-glasses and specular reflections. Occluded region of the candidate iris image leads to an iris code comprising of the bits which are not consistent (fragile) over irises of the same person [6]. A fragile bit is defined as a bit in an iris code which is not consistent across the different iris images of the same subject. Probability of existence of noise at a specific region of iris varies from image to image and hence produces fragile bits in the corresponding iris code. Figure 1 illustrates presence of noise in sample eye images of the same subject, taken from UBIRIS v.2 database, and noise in their unwrapped irises which leads to fragile bits. We propose an iris recognition scheme in which, tracks and sectors are deployed to divide the unwrapped iris region into patches. Earlier researchers have adopted region-wise, multi-patch feature extraction approach for iris classification [11, 13]. Recently Raja et al. [15] have proposed deep sparse filtering on multi patches of normalized mobile iris images. Histograms of each patch are used to represent iris in a collaborative sub space. In our earlier work [18], we have divided the unwrapped iris into M patches using p sectors and q tracks and have utilized Fuzzy c-means clustering algorithm to classify the patches into best iris region and noisy region. We have used probability distribution function in order to cluster the patches into iris or non-iris regions. However, due to varieties of noise present in unconstrained imaging, clustering the iris regions based on their statistical properties alone is difficult. We propose a learning technique which classifies the patches based on bit fragility in each patch using monogenic functions.

Monogenic signals are 2D extensions of 1D analytical signals. An Analytical signal, in its polar representation, gives the information about local phase and amplitude, hence, generalizing 1D analytical signal to its 2D counterpart, using Riesz transform, gives a deeper insight to low level image processing [5]. First order Riesz wavelets can extract 1D inherent signals such as lines and steps in an image and second order Riesz wavelets can capture 2D signals like corners and junctions [9]. In Fig. 2 we have presented example of an unwrapped iris from IITD database, its first order Riesz transformed output responses, $h_{x}(f)$ and $h_{y}(f)$ respectively. We can observe texture variations along horizontal and vertical directions. Further, Riesz transform allows us to extend Hilbert transform along any direction. This property is called steerable property. By the virtue of steerable property, a filter of arbitrary orientation can be created as a linear combination of a collection of basis filters. Steerable Riesz furnishes a substantial computational scheme to extract the local properties of an image.

Fig. 1.

Samples of two eye images of same subject and color maps of their unwrapped irises with noise that leads to fragile bits. (Color figure online)

Fig. 2.

Example of an unwrapped iris from IITD database, its first order Riesz transformed output responses, $h_{x}(f)$ and $h_{y}(f)$ respectively.

A texture learning technique, exploiting local organizations of magnitude and orientations, using steerable Riesz wavelets, has been proposed by Depeursinge [4]. Zhang et al. [21] propose a competitive coding scheme (CompCode) for finger knuckle print (FKP) recognition based on Riesz functions and have obtained promising results for FKP. Two iris coding schemes, based on first and second order Riesz components and steerable Riesz are proposed in [19]. One of the coding scheme encodes responses of two components of first order Riesz and three components of 2nd order Riesz so that each input iris pixel is represented by five binary bits and another scheme generates three bits from steerable Riesz filters. Inspired by these works, we design a descriptor (RSBP) based on 1D and 2D Riesz signals which encodes each pixel into an 8-bit binary pattern. We present detailed explanation of RSBP descriptor and proposed iris recognition scheme in Sect. 2. Result analysis of experiments is discussed in Sect. 3 and we conclude this paper in Sect. 4.

2 Proposed Iris Recognition Scheme

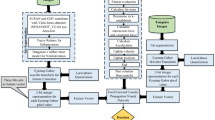
Outline of proposed scheme is demonstrated in Fig. 3. We create M patches of unwrapped iris using p tracks and q sectors. To extract predominant features from each patch, we deploy feature descriptor, Riesz signal based binary pattern (RSBP), which represents each pixel into 8-bit binary code. We adopt Fuzzy c-means clustering (FCM) to learn fragile bits and to cluster the iris patches into five classes, with labels 0 to 4, where 0 refers to non-iris region (with maximum number of fragile bits), and 4 refers to best iris region (with consistent bits). Based on these labels each patch is assigned with a weight. Further, a magnitude weighted phase histogram, proposed in [16], is adopted to represent each patch as 1D real valued feature vector. Dissimilarity between the two iris codes is computed using weighted mean Euclidean distance (WMED).

Fig. 3.

Proposed iris recognition method

2.1 Riesz Functions

Riesz functions are the generalizations of Hilbert functions into d dimensional Euclidean space. If $\mathbf x$ is a d-tuple, $( x_1,x_2,\ldots ,x_d)$ and f is $L^{2}$ measurable d-dimensional function, i.e. $f(\mathbf x )\in L^{2}(\mathbb {R}^d)$, then, Riesz transformation $R^{d}$ of f is a d-dimensional vector signal. $R^{d}f(\mathbf x )$ transforms a signal from $L^{2}(\mathbb {R}^d)$ space to $L^d (\mathbb {R}^d)$ space and is given by,

$$\begin{aligned} {} R^{d}f(\mathbf x )=(R^{d}_{1}f(\mathbf x ), R^{d}_{2}f(\mathbf x ),\ldots ,R^{d}_{d}f(\mathbf x ) ), \end{aligned}$$

(1)

which can be simplified further as follows.

$$\begin{aligned} {} R^{d}f(\mathbf x )=(( h_1*f)(\mathbf x ), (h_2*f)(\mathbf x ),\ldots ,(h_d*f)(\mathbf x ) ), \end{aligned}$$

(2)

where, $*$ represents convolutional operator and $h_{i}$ is d dimensional Riesz kernel which is given by,

$$\begin{aligned} {} h_i=\frac{\varGamma {\frac{(d+1)}{2}}}{\pi ^{(d+1)/2}}\frac{x_i}{\Vert \mathbf{x }\Vert ^{(d+1)}}. \end{aligned}$$

(3)

Further, in 2-D space, taking $\mathbf x = (x,y)$, 2-D Riesz transform is given by,

$$\begin{aligned} {} R^{2}f(\mathbf x )=(( h_x*f)(\mathbf x ), (h_y*f)(\mathbf x )) = (h_{x}f(\mathbf x ),h_{y}f(\mathbf x )), \end{aligned}$$

(4)

where, $h_{x}$ and $h_{y}$ are 2-D Riesz kernels which are obtained by taking $d = 2$ in equation (3).

$$\begin{aligned} {} h_x =\frac{1}{2\pi }\frac{x}{\Vert \mathbf{x }\Vert ^3},\quad h_y = \frac{1}{2\pi }\frac{y}{\Vert \mathbf{x }\Vert ^3}. \end{aligned}$$

(5)

Components in the triplet $(f,h_{x}f,h_{y}f)$ are called first order monogenic components of the function f. Further, when $h_{x}f$ and $h_{y}f$ are convolved with the kernels, $h_{x}$ and $h_{y}$, as the convolution operator is commutative, we get second order components of f as, $(h_{xx}f,h_{xy}f,h_{yy}f)$. One dimensional phase encoding method, based on zero crossings, is used to encode each of the five output signals obtained from first and second order components into binary iris code, so that each pixel in the input iris is represented by five binary bits. We call this iris code as Riesz filter based iris code, RFiC1.

2.2 Steerable Riesz

Because of the steerable property of Riesz filters, response of an $i^{th}$ Riesz component $R_{i}^{d}$ of an oriented image $f^{\theta }$ of an image f, oriented by any arbitrary angle $\theta$, can be derived analytically. It can be computed as linear combinations of responses of all the components as follows.

$$\begin{aligned} {} Rf^\theta (\mathbf x ) = \sum _{i=0}^{d}g_i(\theta )R_{i}^{d}f(\mathbf x ), \end{aligned}$$

(6)

where, $g_i(\theta )$ are coefficient functions or coefficient matrices. Equation (6) can be rewritten as,

$$\begin{aligned} {} Rf^{\theta } = \omega ^{T} R^{d}, \end{aligned}$$

(7)

where $\omega$ is weight vector given by, $\omega = [\omega _{1}, \omega _{2},\omega _{3}]$. We take a steering matrix $M^{\theta }$ proposed in [4] and obtain the linear combination of second order Riesz components $h_{xx}$, $h_{xy}$ and $h_{yy}$ of f as follows.

$$\begin{aligned} {} \begin{aligned} Rf^{\theta }(x,y) = \omega _1M^{\theta }h_{xx}f(x,y)+ \omega _2M^{\theta }h_{xy}f(x,y) +\omega _3M^{\theta }h_{yy}f(x,y) \end{aligned} \end{aligned}$$

(8)

Based on the procedure given in [19], we obtain three more bits from the input pixel. If $\frac{k{\pi }}{n}$, $k=0,1,\ldots ,n-1$ are n orientations of $\theta$ and I(x, y) is the input unwrapped iris, then, at every pixel (x, y), linear sum of steerable Riesz responses $RI^{\theta }(x,y)$ is computed for each orientation $\theta$ using Eq. (8). Thus, each pixel will be having n representations for n orientations. Further, at every point (x, y) an integer value N which varies from 0, to $n-1$ is computed to represent the dominant orientation.

$$\begin{aligned} {} N(x,y) = argmax_{\theta }(RI^{\theta }(x,y)). \end{aligned}$$

(9)

In our experiments, we have taken $n=6$, so that, each pixel has six orientation representations. Equation (9) gives the dominant orientation at (x, y) and generates a matrix consisting of integers from one to six, representing six orientations. These integers from 0 to 5 are represented by a corresponding three bit binary code in the set $\lbrace {000, 001, 011, 111, 110, 100}\rbrace$. These bits combined with $h_{x}f$ and $h_{y}f$, the horizontal and vertical responses, along with a Gabor bit, produce a 6-bit representation of a pixel and the iris code, thus obtained, is called RFiC2.

2.3 Riesz Signal Based Feature Descriptor (RSBP)

Design of RSBP is based on the method by Rajesh and Shekar [16], which uses complex wavelet transform for face recognition. However, we have developed this code on Riesz wavelet transforms. Proposed method is explained in Fig. 4. First and second order Riesz functions are operated on unwrapped iris using convolution operation, to obtain five real valued Riesz responses for each pixel. These responses are encoded into a binary bit using 1D phase informations of zero crossings. Further, steerable Riesz method produces three more bits based on the dominant orientation and thus, we obtain a binary pattern of 8-bits. While computing the decimal equivalent of this binary pattern, we have taken response of first order Riesz along horizontal direction as the most significant bit (MSB) and last bit in steerable Riesz output as LSB. Because, as we observe with experiments, responses of first order horizontal Reisz are more prominent. In Fig. 4 one can observe the distinguished features in RSBP image and in its color map.

Fig. 4.

Riesz signal based binary pattern (RSBP) (Color figure online)

2.4 Iris Code Matching

To explain representation and matching, let $\mathcal {I}^{1}$ and $\mathcal {I}^{2}$ be two unwrapped irises and $\mathcal {I}^{1}_{i}$ and $\mathcal {I}^{2}_{i}$ be the corresponding $i^{th}$ patches, and $\omega ^{1}_{i}$ and $\omega ^{2}_{i}$ be the weights assigned to these patches where $i \in \left\{ 1,2,\dots , M\right\}$, M representing the total number of patches. In order to represent iris features, we adopt the approach in [16]. RSBP image is subdivided into P number of $p_{1} \times q_{1}$ sized sub-blocks. In every sub-block, we compute k bin length histogram. Further, histograms of all of these sub blocks are concatenated to obtain 1D feature vector. We compute the dissimilarity score $Ed_{i}$ between the feature vectors $fv^{1}_{i}$ and $fv^{2}_{i}$, corresponding to the patches $\mathcal {I}^{1}_{i}$ and $\mathcal {I}^{2}_{i}$, using Euclidean distance metric. Taking $\omega _{i}$ as the common weight for both $\mathcal {I}^{1}_{i}$ and $\mathcal {I}^{2}_{i}$, the weighted mean Euclidean distance (WMED) between the two irises is calculated by,

$$\begin{aligned} Ed(\mathcal {I}^{1},\mathcal {I}^{2}) = \frac{\sum \omega _{i}Ed_{i}}{\sum \omega _{i}} \end{aligned}$$

(10)

When both $\mathcal {I}^{1}_{i}$ and $\mathcal {I}^{2}_{i}$ have non zero weights, $\omega _{i}$ will be the maximum of the weights $\omega ^{1}_{i}$ and $\omega ^{2}_{i}$ and when one of them has zero weight, then $\omega _{i}$ is set to zero.

3 Experimental Analysis

To justify the applicability of our scheme for iris recognition, we have experimented our approach on the benchmark NIR iris datasets IITD [8], MMU v-2 [2], CASIA-IrisV4-Distance [1] and VW dataset UBIRIS.v2 [14] and the results are compared with state-of-the-art publications which have worked on the same datasets. In this work, our primary objective is iris feature extraction and representation. Hence, iris segmentation is done using the approach given in [18] and for unwrapping (normalization), Daugman’s rubber sheet model [3] is adopted. Regarding the parameter set up for our experiments, in case of NIR images, resolution for unwrapping is $64 \times 256$ and for UBIRIS v.2 it is $64 \times 512$. Using 2 tracks and 8 sectors, we divide the unwrapped iris into 16 patches so that, each patch is of size $32 \times 32$ for NIR images and $32 \times 64$ for VW images. We have conducted the experiments in two scenarios, without multi-patches and with multi-patches using the coding methods RFiC1, RFiC2 and RSBP. RFiC1 and RFiC2 represent the iris into binary-bit patterns and hence Daugman’s Hamming distance is used to find the dissimilarity score. Size of Riesz kernel is set to 15 [19]. FCM is trained with 60% of the images ($60 \% \times 16$ number of patches) from each of the dataset, so that training to test ratio is 3:2.

Discussion: We have used the equal error rate (EER), $d-prime$ values and ROC curve to evaluate proposed technique for comparison and analysis. In Table 1 we present the results of our experiments conducted without multi-patches scenario (S1) and with multi-patches scenario (S2). We observed average decrease of 7.9% in EER values and increase of 5.9% in $d-prime$ values from S1 to S2. With RSBP method there is 9.48% of decrease in average EER value and 6.7% of increase in $d-prime$ value. ROC curves of these experiments are presented in Fig. 5.

Table 1. EER and $d-prime$ values obtained by proposed methods with respect to different datasets without (S1) and with (S2) multi-patches.

Fig. 5.

ROC curves of the RFiC1, RFiC2 and RSBP obtained on MMU dataset without and with multi-patches approach respectively.

We compare the proposed technique with the state-of-art methods which work on fragile bits or multi-patches techniques. Results of comparison analysis are presented in the Table 2. In [12] author compare the usefulness of different regions of the iris for recognition using bit-discriminability. Kaur et al. [7] have computed discrete orthogonal moment-based features on the ROI divisions of the unwrapped iris. Vyas et al. [20] have extracted gray level co-occurrence matrix (GLCM) based features from multiple blocks of normalized iris templates and concatenated them to form the feature vector. Since, these authors have worked with multi-patches concept on the same datasets, we have compared their published results with our results and the figures displayed in Table 2 illustrate that our method compares favourably with existing approaches.

Table 2. EER and $d-prime$ values with respect to UBIRIS v.2 and IITD databases compared with the recent related publications. NA implies not available.

4 Conclusion

Fragile bits present in an iris code mainly increase the intra-class variations, thereby increasing false reject rate. Proposed method uses the fragile bit information to rank the iris regions by assigning the weights which are further used in matching the iris code and hence, the intra-class variations are suppressed and at the same time inter-class variations are enhanced. We have also proposed a new iris feature extraction and representation approach using a descriptor RSBP, based on 1D and 2D Riesz transformations and experiments illustrate that it is well suited for iris recognition.