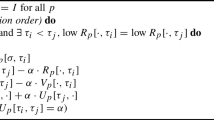Keywords

1 Introduction

Topological Data Analysis combines machine learning with topological methods, most importantly persistent homology [10, 12]. The underlying idea is that data has shape and this shape contains information about the data-generating process [4]. Persistent homology is a method to characterize topological features that occur in data at multiple scales. Its theoretical properties, in particular the structure theorem and the stability theorem make persistent homology an attractive machine learning method.

A major obstacle to the wide-spread use of persistent homology is its computational complexity when analyzing large datasets. For example the Čech complex grows exponentially with the number of points in a point cloud. In order to be able to calculate persistent homology, a number of approximations enable us to reduce the computational complexity of persistent homology calculations [3, 5, 6, 8].

Recently, Blaser and Brun have presented methods to sparsify nerves that arise from general Dowker dissimilarities [1, 2]. In this article, we apply these techniques to calculate the persistent homology of point clouds, weighted networks and more general filtered covers. This paper is focused on the algorithm implementation, computational complexity and benchmarking of methods suggested in Blaser and Brun [2].

All algorithms presented in this manuscript are implemented in the python package dowker_homology, available on github. With dowker_homology it is possible to calculate persistent homology of ambient Čech filtrations, and intrinsic Čech filtrations of point clouds, weighted networks and general finite filtered covers. The dowker_homology package does all the preprocessing and sparsification, and relies on GUDHI [13] for calculating persistent homology. Users may specify additive interleaving, multiplicative interleaving or arbitrary interleaving functions.

This paper is organized as follows. In Sect. 2, we give a short introduction on the underlying theory of the methods presented here. Section 3 presents the implemented algorithms in detail. In Sect. 4 we quickly discuss the size complexity of the sparse nerve and in Sect. 5 we provide detailed benchmarks comparing the sparse Dowker nerve to other sparsification strategies. Section 6 is a short summary of results.

2 Theory

The theory is described in detail in [2]. In brief, the algorithm consists of two steps, a truncation and a restriction. Given a Dowker dissimilarity \(\varLambda \), the truncation gives a new Dowker dissimilarity \(\varGamma \) that satisfies a desired interleaving guarantee. The restriction constructs a filtered simplicial complex that is homotopy equivalent to, but smaller than the filtered nerve of \(\varGamma \). The paper [2] gives a detailed description of the sufficient conditions for a truncation and restriction to satisfy a given interleaving guarantee. Here we give a new algorithm to choose a truncation and restriction that together result in a small sparse nerve. In Sect. 5, we compare sparse nerve sizes from the algorithms presented here with the sparse nerve sizes of the algorithms presented in [1] and [2].

3 Algorithms

We present all algorithms given a finite Dowker dissimilarity. Generating a finite Dowker dissimilarity from data is a precomputing step that we do not cover in detail. For the intrinsic Čech complex of \(n\) data points in Euclidean space \(\mathbb {R}^d\), this consists of calculating the distance matrix, with time complexity \(\mathcal {O}(n^2 \cdot d)\) operation.

3.1 Cover Matrix

The cover matrix is defined in [2, Definition 5.4]. Let \(\varLambda :L \times W \rightarrow [0,\infty ]\) be a Dowker dissimilarity. Given \(l,l'\in L\) let

$$\begin{aligned} P(l,l') = \{ \varLambda (l',w) \, \mid \, w \in W \text { with } \varLambda (l,w) < \varLambda (l',w) \} \end{aligned}$$

and define the cover matrix \(\rho \) as

More generally, we can define a cover matrix of two Dowker dissimilarities \(\varLambda _1 :L \times W \rightarrow [0,\infty ]\) and \(\varLambda _2 :L \times W \rightarrow [0,\infty ]\) as follows.

$$\begin{aligned} P(l,l') = \{ \varLambda _1(l',w) \, \mid \, w \in W \text { with } \varLambda _2(l,w) < \varLambda _1(l',w) \} \end{aligned}$$

and define the cover matrix \(\rho \) as before. We define the cover matrix algorithm in this generality, but sometimes we will use it with just one Dowker dissimilarity \(\varLambda \), in which case we implicitly use \(\varLambda _1 = \varLambda _2 = \varLambda \).

Our algorithms for calculating the truncated Dowker dissimilarity and for calculating a parent function both rely on the cover matrix. The cover matrix is the mechanism for the two algorithms to interoperate. Algorithm 1 explains how the cover matrix can be calculated from two Dowker dissimilarities.

figure a

The cover matrix algorithm is the bottleneck for calculating the truncated Dowker dissimilarity and the parent function. Its running time \(\mathcal {O}(|L|^2 \cdot |W|)\) is quadratic in the size of \(L\) and linear in the size of \(W\).

3.2 Truncation

Given a Dowker dissimilarity \(\varLambda :L \times W \rightarrow [0,\infty ]\), and a translation function \(\alpha :[0,\infty ]\rightarrow [0,\infty ]\), every Dowker dissimilarity \(\varGamma :L \times W \rightarrow [0,\infty ]\) satisfying \(\varLambda (l, w) \le \varGamma (l, w) \le \alpha (\varLambda (l, w))\), is \(\alpha \)-interleaved with \(\varGamma \). In the case where \(\alpha \) is multiplication by a constant, both extremes \(\varLambda (l, w)\) and \(\alpha (\varLambda (l, w))\) will result in restrictions with sparse nerves of the same size. Our goal is to find a truncation that interacts well with the restriction presented in Sect. 3.4 in order to produce a small sparse nerve.

Algorithm 2 explains in detail, how the truncated Dowker dissimilarity is calculated. The high level view is that we first calculate a farthest point sampling from the cover matrix and the edge list \(E\) of the hierarchical tree of farthest points. Finally, we iteratively reduce \(\varGamma (l, w)\) starting from \(\alpha (\varLambda (l, w))\) by taking the minimum of \(\varGamma (l, w)\) and \(\varGamma (l', w)\) for \((l', l)\) in \(E\).

figure b

The truncation algorithm has a worst-case time-complexity \(\mathcal {O}(|L|^2 \cdot |W|)\). As mentioned earlier, calculating the cover matrix is the bottleneck. The time complexity of the while loop is \(\mathcal {O}(|L|^2)\), sorting is \(\mathcal {O}(|L| \cdot \log |L|)\), the first for loop is \(\mathcal {O}(|L|^2)\), the topological sort of a tree is \(\mathcal {O}(|L|)\), and the last for loop is \(\mathcal {O}(|L| \cdot |W|)\).

3.3 Parent Function

The parent function \(\varphi :L \rightarrow L\) can in principle be any function such that the graph \(G\) consisting of all edges \((l, \varphi (l))\) with \(l \ne \varphi (l)\), is a tree.

Here we present the algorithm to create one particular parent function that works well in practice and combined with the truncation presented in Sect. 3.2 results in small sparse nerves.

Algorithm 3 is a greedy algorithm. Ideally, we would like to set the parent point of any point \(l \in L\) as the point \(l' \in L\) that minimizes \(\rho (l, l'')\) for \(l'' \in L\) with \(\rho (l, l'') > 0\). However, this may not result in a proper parent function. Therefore we start with this as a draft parent function and then update it so that it becomes a proper parent function.

figure c

The time complexity of calculating the cover matrix is \(\mathcal {O}(|L|^2 \cdot |W|)\). Every subsequent step can be done in at most \(\mathcal {O}(|L|^2)\) time.

3.4 Restriction

Given a set of parent points \(\varphi (l)\) for \(l \in L\) and the cover matrix \(\rho :L \times L \rightarrow [0,\infty ]\), Algorithm 4 calculates the minimal restriction function \(R: L \rightarrow [0,\infty ]\) given in [2, Definition 5.4, Proposition 5.5].

figure d

The restriction algorithm has a worst-case quadratic time-complexity \(\mathcal {O}(|L| ^ 2)\). The first loop is linear in the size of \(L\), while the second loop depends on the depth \(td(G)\) of the parent tree \(G\). For a given parent tree depth, the complexity is \(\mathcal {O}(|L| \cdot td(G))\).

3.5 Sparse Nerve

In order to calculate persistent homology up to homological dimension \(d\), we calculate the \((d+1)\)-skeleton \(N\) of the sparse filtered nerve of \(\varGamma \). Given the truncated Dowker dissimilarity \(\varGamma \), the parent tree \(\varphi \) and the restriction times \(R\), Algorithm 5 calculates the \((d+1)\)-skeleton \(N\). Note that the filtration values can be calculated either from \(\varGamma \) or directly from \(\varLambda \).

figure e

The time complexity of the sparse nerve algorithm is \(\mathcal {O}(|L|^2 \cdot |W| + |N|\log (|N|))\). The loop to find slope points had time complexity \(\mathcal {O}(|L|^2)\) The loop for finding maximal faces has a time complexity of \(\mathcal {O}(|L|^2 \cdot |W|)\). The remaining operations have time complexity \(\mathcal {O}(|N|\log (|N|)\). Calculating persistent homology using the standard algorithm is cubic in the number of simplices.

So far we have considered the case of a Dowker dissimilarity \(\varLambda :L \times W \rightarrow [0,\infty ]\) with finite \(L\) and \(W\). This includes for example the intrinsic Čech complex of any finite point cloud \(X\) in a metric space \((M, d)\), where \(L = W = X\) and \(\varLambda = d\).

3.6 Ambient Čech Complex

Let \(X\) be a finite subset of Euclidean space \(\mathbb {R}^n\) and consider its ambient Čech complex. For \(L = X\) and \(W = \mathbb {R}^n\), the Dowker nerve of \(\varLambda = d|_{L\times W}\) is the ambient Čech complex of \(X\). Since \(W\) is not finite we have to modify our approach slightly to in order to construct a sparse approximation of the Dowker nerve of \(\varLambda \).

We first calculate the restriction function \(R'(l)\) for \(l \in L\) of the intrinsic Čech complex \(\varLambda ' = \varLambda |_{L\times L}\). Then we note that \(R(l) = 2R'(l)\) is a restriction function for \(\varLambda \) [2, Definition 5.3]. We can use Algorithm 5 to calculate the simplicial complex \(N\) using the restriction times \(R\) and Dowker dissimilarity \(\varLambda '\). However, since \(W\) is infinite, we can not directly compute the minimum used to calculate the filtration values \(v(\sigma )\) for \(\sigma \in N\). We circumvent this problem by considering a filtered simplicial complex \(K\) with the same underlying simplicial complex as \(N\), but with filtration values inherited from the Dowker nerve \(N\varLambda \). This means that the filtration values are computed with the miniball algorithm. Thus, we construct a filtered simplicial complex \(K\), such that, for all \(t \in [0, \infty ]\) we have

$$\begin{aligned} N_t \subseteq K_t \subseteq N\varLambda _t. \end{aligned}$$

Since \(N\) is \(\alpha \)-interleaved with \(N\varLambda \), it follows by [2, Lemma 2.14] that also \(K\) is \(\alpha \)-interleaved with \(N\varLambda \).

3.7 Interleaving Lines

Our approximations to Čech- and Dowker nerves are interleaved with the original Čech- and Dowker nerves. As a consequence their persistence diagrams are interleaved with the persistence diagrams of the original filtered complexes. In order to visualize where the points may lie in the original persistence diagrams, we can draw the matching boxes from [2, Theorem 3.9]. However, this result in messy graphics with lots of overlapping boxes. Instead of drawing these matching boxes we draw a single interleaving line. Points strictly above the line in the persistence diagram of the approximation match points strictly above the diagonal in the persistence diagram of the original filtered simplicial complex. More precisely, the matching boxes of points above the interleaving line do not cross the diagonal, while the matching boxes of all points below the diagonal have a non-empty intersection with the diagonal. Figure 1 illustrates such an interleaving line for \(100\) data points on a Clifford torus with interleaving \(\alpha (x) = \frac{x^3}{2} + x + 0.3\).

Fig. 1.
figure 1

Interleaving line. We generated \(100\) points on a Clifford torus that and calculated sparse persistent homology with an interleaving of \(\alpha (x) = \frac{x^3}{2} + x + 0.3\). This demonstrates the interleaving line for a general interleaving. Points above the line are guaranteed to have matching points in the persistence diagram with interleaving \(\alpha (x) = x\).

Full size image

4 Complexity Analysis

We have shown time complexity analysis of each step. Combined, the time it takes to calculate the sparse filtered nerve is \(\mathcal {O}(|L|^2 \cdot |W| + |N|\log (|N|))\). Here we present some results on the complexity of the nerve size depending on the maximal homology dimension \(d\) and the sizes of the domain spaces \(L\) and \(W\) of the Dowker dissimilarity \(\varLambda : L\times W \rightarrow [0,\infty ]\). Although we can not show that the sparse filtered nerve is small in the general case, we will show in the benchmarks below that this is the case for many real-world datasets.

We now limit our analysis to Dowker dissimilarities that come from doubling metrics and multiplicative interleavings with an interleaving constant \(c>1\). In that case, Blaser and Brun [2] have showed that the size of the sparse nerve is bounded by the size of the simplicial complex by Cavanna et al. [5], whose size is linear in the number \(|L|\) of points.

5 Benchmarks

We show benchmarks for two different types of datasets, namely data from metric spaces and data from networks.

Metric Data. We have applied the presented algorithm to the datasets from Otter et al. [11]. First we split the data into two groups, data in \(\mathbb {R}^d\) with dimension \(d\) at most \(10\) and data of dimension \(d\) larger than \(10\). The low-dimensional datasets we studied consisted of six different Vicsek datasets (Vic1-Vic6), dragon datasets with 1000 (drag1) and 2000 (drag2) points and random normal data in 4 (rand4) and 8 (rand8) dimensions. For all low-dimensional datasets, we compared the sparsification method from Cavanna et al. [5] termed ‘Sheehy’, the method from [1] termed ‘Parent’ and the algorithm presented in this paper termed ‘Dowker’ for the intrinsic Čech complex. All methods were tested with a multiplicative interleaving of \(3.0\). In addition to the methods described above, we have applied SimBa [8] with \(c = 1.1\) to all datasets. Note that SimBa approximates the Rips complex with an interleaving guarantee larger than \(3.0\). For the \(3\)-dimensional data we additionally compute the alpha-complex without any interleaving [9]. For all algorithms we calculate the size of the simplicial complex used to calculate persistent homology up to dimension \(1\) (Table 1).

Table 1. Comparison of sizes of simplicial complexes for homology dimension 1 for low-dimensional datasets in Euclidean space. The smallest simplicial complexes in each dimension are displayed in bold. For all three-dimensional datasets, SimBa results in slightly smaller simplicial complexes. For the two datasets of dimensions larger than three, the Dowker simplicial complex is smallest.
Full size table

The sparse Dowker nerve is always smaller than the sparse Parent and sparse Sheehy nerves. In comparison to SimBa, it is noticeable that the SimBa results in slightly smaller simplicial complexes if the data dimension is three, but the sparse Dowker Nerve is smaller for most datasets in dimensions larger than \(3\). For datasets of dimension \(3\), the alpha complex without any interleaving is already smaller than the Parent or Sheehy interleaving strategies, but Dowker sparsification and SimBa can reduce sizes further.

The high-dimensional datasets we studied consisted of the H3N2 data (H3N2), the HIV-1 data (HIV), the Celegans data (eleg), fractal network data with distances between nodes given uniformly at random (f-ran) or with a linear weight-degree correlations (f-lin), house voting data (hou), human gene data (hum), collaboration network (net), multivariate random normal data in 16 dimensions (ran16) and senate voting data (sen).

For all high-dimensional datasets, we compared the intrinsic Čech complex sparsified by the algorithm presented in this paper (‘Dowker’) with a multiplicative interleaving of \(3.0\) to the Rips complex sparsified by SimBa [8] with \(c = 1.1\). For the high-dimensional datasets, we do not consider the ‘Sheehy’ and ‘Parent’ methods, because they take too long to compute and are theoretically dominated by the ‘Dowker’ algorithm. For all algorithms we calculate the size of the simplicial complex used to calculate persistent homology up to dimensions \(1\) and \(10\) (Table 2).

Table 2. Comparison of sizes of simplicial complexes for homology dimensions 1 and 10 for high-dimensional datasets in Euclidean space. The smallest simplicial complexes in each dimension are displayed in bold. Except for one dataset, the Dowker sparsifications result in smaller simplicial complexes than SimBa. Note that we write \(\infty \) when the computer ran out of memory.
Full size table

In comparison to SimBa, it is noticeable that the SimBa, the Dowker Nerve is smaller for most datasets, with a more pronounced difference for persistent homology in \(10\) dimensions.

Table 3. Comparison of sizes of simplicial complexes for homology dimensions 1 and 10 for graphs with 100 nodes. For the \(1\)-dimensional case, we show that the Dowker restriction can in some cases reduce the simplicial complex significantly even without any truncation.
Full size table

Graph Data. In order to treat data that does not come from a metric, we calculated persistent homology from a Dowker filtration [7]. Table 3 shows the sizes of simplicial complexes to calculate persistent homology in dimensions \(1\) and \(10\) of several different graphs with \(100\) nodes. In both cases we calculated persistent homology with a multiplicative interleaving \(\alpha = 3\), and for the \(1\)-dimensional case we also calculated exact persistent homology. For the \(1\)-dimensional case, the base nerves are always of the same size \(166750\), the restricted simplicial complexes for exact persistent homology range from \(199\) to \(166750\), while the simplicial complexes for interleaved persistent homology have sizes between \(199\) and \(721\). The simplicial complexes to calculate persistent homology in \(10\) dimensions do not grow much larger when multiplicative interleaving is \(3\).

6 Conclusions

We have presented a new algorithm for constructing a sparse nerve and have shown in benchmark examples that its size does not grow substantially for increasing data or homology dimension and that it in many cases outperforms SimBa. In addition, the presented algorithm is more flexible than previous sparsification strategies in the sense that it works for arbitrary Dowker dissimilarities and interleavings. We also provide a python package dowker_homology that implements the presented sparsification strategy.