Abstract
For the discrete-time superreplication problem, a guaranteed deterministic formulation is proposed: the problem is to ensure the cheapest coverage of the contingent claim on an American option under all admissible scenarios. These scenarios are set by a priori defined compacts depending on the price history; the price increment at each moment of time must lie in the corresponding compact. The market is considered without trading constraints and transaction costs. The problem statement is game-theoretic in nature and leads directly to the Bellman–Isaacs equations of a special form under the assumption of no trading constraints. In the present study, we estimate the modulus of continuity of uniformly continuous solutions, including the Lipschitz case.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The increments are taken “backward”, i.e., ΔX t = X t − X t−1, where X t is a discounted price vector at time t.
- 2.
We suppose that a risk-free asset has a fixed price equal to one.
- 3.
The point indicates the variables representing the price evolution. More precisely, prehistory \( \bar {x}_{t-1}=(x_0,\ldots , x_{t-1})\in (\mathbb {R}^n)^t \) for K t, whereas it is the history \( \bar {x}_t=(x_0,\ldots , x_{t})\in (\mathbb {R}^n)^{t+1} \) for the functions \( v^*_t \) and g t introduced below.
- 4.
The sign
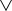 denotes the maximum; hy = 〈h, y〉 is the dot product of vector h by vector y.
denotes the maximum; hy = 〈h, y〉 is the dot product of vector h by vector y. - 5.
Neighborhoods of points −∞ and + ∞ are given by [∞, a), \(a \in \mathbb {R}\) and (b, +∞], \(b \in \mathbb {R}\), respectively.
- 6.
Here, x + A = {z : z − x ∈ A}.
- 7.
It can be interpreted as the guaranteed profit for a strategy h ∈ D t(⋅). Note that \( \min \{hy,\; y\in K_t (\cdot )\} \) is attained due to the compactness of K t(⋅) for some (worst scenario) \( y_h^*\in K_t (\cdot ) \); it is positive for the sure arbitrage strategy h ∗∈ D t(⋅).
- 8.
Here, 2 T is the class of all subsets of T.
- 9.
In this case, considering the property 10, the subadditivity holds trivially.
- 10.
Wherein, it is possible that ω(δ)=∞ for all δ > 0. If ω satisfies the conditions 10, 20 and 50, then, for 30, it is sufficient that ω(δ) is finite at a point δ > 0.
- 11.
For such a function φ, the conditions of Remark 14.1 clause 2) are satisfied.
- 12.
A similar statement can be found in the literature; see, for example, Sect. 6 in the book [2]; however, there are redundant requirements on φ.
- 13.
If, in addition to 10 and 20, the function is concave, then 40 and 50 are fulfilled.
- 14.
More precisely, it is a continuation of the Cantor function ψ : [0, 1]↦[0, 1], setting φ(δ) = 1 when δ > 1.
- 15.
This property can be considered a continuous version of the Fekete lemma.
- 16.
As the additive function, i.e., the solution of the Cauchy equation, is subadditive, then, without additional conditions, it is impossible to obtain asymptotic linearity for the subadditive function, because the axiom of choice implies the existence of a solution (not measurable) of the Cauchy equation such that its graph is dense everywhere on the plane [6]. It suffices to require the boundness of ω in a neighborhood of the point 0; in our case, this follows from the nonnegativity of ω (a consequence of the properties of 10 and 20) and the properties of monotonicity of 20 and the finiteness 30.
- 17.
If a function ω, satisfying 10 and 20, is concave, then the function \(t \to \frac {\omega (t))}{t}\) is non-increasing.
- 18.
It is possible that h ρ(A, B) = ∞.
- 19.
Recall that hy denotes the inner product.
- 20.
For such arguments, the function r takes finite non-negative values.
- 21.
- 22.
Here, \( \operatorname *{\mathrm {aff}}(N)\) is the affine hull of N (that is the smallest affine set containing N, see [13, Section 1]); \(\dim (A)\) is the dimension of an affine space A.
- 23.
Here, \( \operatorname *{\mathrm {ri}}(A) \) denotes the relative interior of a convex set A, that is the interior of A with respect to the relative topology on \( \operatorname *{\mathrm {aff}}(A)\subseteq \mathbb {R}^n \), see [13, Section 6].
- 24.
At least, with respect to the functions of potential payments g t, t = 1, …, N, this is not only convenient, but also natural, as, usually, it is how these functions are defined in practice.
- 25.
For compact-valued mappings, h-continuity is equivalent to continuity; see Theorem 2.68 from [5].
- 26.
See, for example, Theorem 3.16.5 from [3].
- 27.
See, for example,Theorem 5.1 and Lemma 5.5 from [8].
- 28.
Here, the Lipschitz constants can be considered as minimal, i.e., \( L_ {g_{t-1}} = \sup \{\omega _{g_{t-1}} (\delta ) / \delta , \; \delta > 0 \} \), \( L_{K_{t-1}} = \sup \{\omega _{K_ {t-1}} (\delta ) / \delta , \; \delta > 0 \} \).
- 29.
Also called the digital option.
- 30.
This terminology was introduced in [9].
References
Bernhard, P., Engwerda, J.C., Roorda, B., Schumacher, J., Kolokoltsov, V., Saint-Pierre, P., Aubin, J.-P.: The Interval Market Model in Mathematical Finance: Game-Theoretic Methods, p. 348. Springer, New York (2013)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation, p. 452. Springer, New York (1993)
Diedonné, J.: Foundations of Modern Analysis, p. 361. Academic, New York (1960)
Dovgoshey, O., Martio, O., Ryazanov, V., Vuorinen, M.: The Cantor function. Expo. Math. 24(1), 1–37 (2006)
Hu, S., Papageorgiou, N.: Handbook of Multivalued Analysis: Theory, vol. I. Mathematics and Its Applications, vol. 419, p. 968. Springer, Berlin (1997)
Jones, F.B.: Connected and disconnected plane sets and the functional equation f(x + y) = f(x) + f(y). Bull. Am. Math. Soc. 48, 115–120 (1942)
Leichtweiss, K.: Konvexe Mengen, p. 330. Springer, Berlin (1980) (in German)
Polovinkin, E.S.: Mnogoznachniy analiz i differencialniye vklucheniya [Set-valued analysis and differential inclusions], p. 524. Nauka, FizMatLit Publication, Moscow (2015) (in Russian)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: financial market model, trading constraints and Bellman–Isaacs equations. Math. Game Theory Appl. 10(4), 59–99 (2018) (in Russian)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: no arbitrage market condition. Math. Game Theory Appl. 11(2), 68–95 (2019) (in Russian)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: the proprieties of semicontinuity and continuity of the Bellman–Isaacs equations. Math. Game Theory Appl. (2019, in print) (in Russian)
Titman, A.F.: Theory of approximation of functions of a real variable. In: International Series of Monographs in Pure and Applied Mathematics, vol. 34, p. 644. Pergamon Press, Oxford (1963)
Rockafellar, R.T.: Convex Analysis, p. 451. Princeton University Press, Princeton (1970)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Smirnov, S.N. (2019). Guaranteed Deterministic Approach to Superhedging: Lipschitz Properties of Solutions of the Bellman–Isaacs Equations. In: Petrosyan, L., Mazalov, V., Zenkevich, N. (eds) Frontiers of Dynamic Games. Static & Dynamic Game Theory: Foundations & Applications. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-23699-1_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-23699-1_14
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-23698-4
Online ISBN: 978-3-030-23699-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



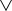 denotes the maximum; hy = 〈h, y〉 is the dot product of vector h by vector y.
denotes the maximum; hy = 〈h, y〉 is the dot product of vector h by vector y.