An Implementation of a Coupled Dual-Porosity-Stokes Model with FEniCS

Abstract

Porous media and conduit coupled systems are heavily used in a variety of areas. A coupled dual-porosity-Stokes model has been proposed to simulate the fluid flow in a dual-porosity media and conduits coupled system. In this paper, we propose an implementation of this multi-physics model. We solve the system with the automated high performance differential equation solving environment FEniCS. Tests of the convergence rate of our implementation in both 2D and 3D are conducted in this paper. We also give tests on performance and scalability of our implementation.

1 Introduction

The coupling of porous media flow and free flow is of importance in multiple areas, including groundwater system, petroleum extraction, and biochemical transport [1,2,3]. The Stokes-Darcy equation is widely applied in these areas and has been studied thoroughly over the past decade [4,5,6]. Variants of Stokes-Darcy mode, have also been studied extensively [7,8,9,10].

In a traditional Stokes-Darcy system, Darcy’s law is applied to the fluid in porous media. Darcy’s law, along with its variants, is great in modeling single porosity model with limited Reynolds number, and is widely used in hydrogeology and reservoir engineering. However, for a porous medium with multiple porosities, for example a naturally fractured reservoir, the accuracy of Darcy’s law is limited. In contrast, a dual-porosity model assumes two different systems inside a porous media-: the matrix system and the microfracture system. These two systems have significantly different fluid storage and conductivity properties. It gives a better representation of the fractured porous media encountered in hydrology, carbon sequestration, geothermal systems, and petroleum extraction [11,12,13].

The dual-porosity model itself fails to consider large conduits inside porous media. Thus, the need of coupling both a dual-porosity model with free flow arises [14].

Our paper expands on a coupled Dual-Porosity-Stokes model [15]. Similar to the Stokes-Darcy model, this coupled model contains two nonoverlapping but contiguous regions: one filled with porous media and the other represents conduits. The dual-porosity model describes the porous media and the Stokes equation governs the free flow in the conduits.

In Sect. 2, we define the Dual-Porosity-Stokes model. The equations are presented as well as the variational form. In Sect. 3, we describe the numerical implementation using FEniCS. In Sect. 4, we analyze the accuracy, speed performance, memory usage, and scalability of our implementation. In Sect. 5, we draw some conclusions and discuss future work.

2 Dual-Porosity-Stokes Model

The Dual-Porosity-Stokes model was first presented in [15]. This paper demonstrated the well-posedness of the model and derived a numerical solution in 2D using a finite element method. Several numerical experiments are also in the paper. In this section we will demonstrate this model in detail as well as present the variational form.

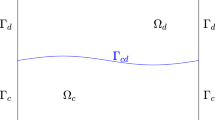
To better understand the model, let us first take a look at a simple 2D example presented in Fig. 1. The model consists of a dual-porosity subdomain $\Omega _{d}$ and a conduit subdomain $\Omega _{c}$, with an interface $\Gamma _{cd}$ in between. Two subdomains are non-overlapping, and only communicate to each other through the interface $\Gamma _{cd}$. $\Gamma _{d}$ and $\Gamma _{c}$ are boundaries of each subsystem.

Fig. 1.

Coupled model in 2D

Two fluid pressures are presented in $\Omega _{d}$, $p_{m}$ and $p_{f}$, for fluids in matrix and fractures respectively. The $m$ subscript stands for matrix and $f$ is for fracture. We use these two subscripts for other model parameters. The dual-porosity model can be expressed as:

$$ \phi_{m} C_{mt} \frac{{\partial p_{m} }}{\partial t} - \nabla \cdot \frac{{k_{m} }}{\mu }\nabla p_{m} = - Q , $$

(1)

$$ \phi_{f} C_{ft} \frac{{\partial p_{f} }}{\partial t} - \nabla \cdot \frac{{k_{f} }}{\mu }\nabla p_{f} = Q + q_{p} . $$

(2)

The constant $\sigma$ is a shape factor ranging from 0 to 1. It measures the connectivity between the microfracture and the matrix. $\mu$ is the dynamic viscosity. $k$ is the intrinsic permeability. $\phi$ denotes the porosity. $C_{mt}$ and $C_{ft}$ denote the total compressibility for the two systems respectively. $q_{p}$ is the sink/source term. $Q$ is the mass exchange between matrix and microfracture systems and can be derived from $Q = \frac{{\sigma k_{m} }}{\mu } \left( {p_{m} - p_{f} } \right)$.

In the conduit subdomain, we use the linear incompressible Stokes equation to describe the free flow:

$$ \frac{{\partial \varvec{u}_{c} }}{\partial t} - \nabla \cdot {\mathbb{T}}\left( {\varvec{u}_{c} ,p} \right) = \varvec{f}, $$

(3)

$$ \nabla \cdot \varvec{u}_{c} = 0 . $$

(4)

The flow velocity $\varvec{u}_{c}$ and pressure $p$ together describe the free flow. $\nu$ is the kinematic viscosity. $\varvec{f}$ is a general source term. ${\mathbb{T}}\left( {\varvec{u}_{c} , p} \right)\text{ := } 2\nu {\mathbb{D}}\left( {\varvec{u}_{c} } \right) - p{\mathbb{I}}$ is the stress tensor, where ${\mathbb{D}}\left( {\varvec{u}_{c} } \right)\text{ := }\frac{1}{2} \left( {\nabla \varvec{u}_{c} + \nabla^{T} \varvec{u}_{c} } \right)$ is the deformation tensor, and ${\mathbb{I}}$ is the $N \times N$ identity matrix.

On the interface $\Gamma _{cd}$, a no-exchange condition between the matrix and the conduit is used,

$$ \begin{array}{*{20}c} { - \frac{{k_{m} }}{\mu }\nabla p_{m} \cdot \left( { - \varvec{n}_{cd} } \right) = 0 ,} \\ \end{array} $$

(5)

where $\varvec{n}_{cd}$ is the unit normal vector on the interface pointing toward $\Omega _{d}$. This equation forces the fluid in the matrix to stay in the porous media. It is based on the fact that the permeability of the matrix system is usually $10^{5}$ to $10^{7}$ times smaller than the microfracture permeability [16,17,18,19].

Three more interface conditions are derived from Stokes-Darcy model:

$$ \varvec{u}_{c} \cdot \varvec{n}_{cd} = - \frac{{k_{f} }}{\mu }\nabla p_{f} \cdot \varvec{n}_{cd} , $$

(6)

$$ - \varvec{n}_{cd}^{T} {\mathbb{T}}\left( {\varvec{u}_{c} ,p} \right)\varvec{n}_{cd} = \frac{{p_{f} }}{\rho } , $$

(7)

$$ - {\mathbb{P}}_{\tau } \left( {{\mathbb{T}}\left( {\varvec{u}_{c} ,p} \right)\varvec{n}_{cd} } \right) = \frac{\alpha \nu \sqrt N }{{\sqrt {{\text{trace}}\left( {\varvec{\Pi}} \right)} }}\left( {\varvec{u}_{c} + \frac{{k_{f} }}{\mu }\nabla p_{f} } \right) . $$

(8)

$\rho$ is the density of the fluid. ${\mathbb{P}}_{\tau }$ is the projection operator onto the local tangent plane of the interface $\Gamma _{cd}$. $\alpha$ is a dimensionless parameter which depends on the properties of the fluid and the permeable material, $N$ is the space dimension, and ${\varvec{\Pi}} = k_{f} {\mathbb{I}}$ is the intrinsic permeability of the fracture media. Condition (6) is the conservation of mass on the interface. Equation (7) represents the balance of forces on the interface [20, 21]. Equation (8) is the Beavers-Joseph interface condition [22].

If we introduce a vector valued test function $\vec{\varvec{v}} = \left[ {\psi_{m} , \psi_{f} , \varvec{v}^{T} , q} \right]^{T}$, the variational form for our model can be written as

$$ \mathop \smallint \nolimits_{{\Omega _{d} }} \left( {\phi_{m} C_{mt} \frac{{\partial p_{m} }}{\partial t}\psi_{m} + \frac{{k_{m} }}{\mu }\nabla p_{m} \cdot \nabla \psi_{m} + \frac{{\sigma k_{m} }}{\mu }\left( {p_{m} - p_{f} } \right)\psi_{m} } \right){\text{d}}\Omega $$

(9a)

$$ + \mathop \smallint \nolimits_{{\Omega _{d} }} \left( {\phi_{f} C_{ft} \frac{{\partial p_{f} }}{\partial t}\psi_{f} + \frac{{k_{f} }}{\mu }\nabla p_{f} \cdot \nabla \psi_{f} + \frac{{\sigma k_{m} }}{\mu }\left( {p_{f} - p_{m} } \right)\psi_{f} } \right)d\Omega $$

(9b)

$$ + \eta \mathop \smallint \nolimits_{{\Omega _{c} }} \left( {\frac{{\partial \varvec{u}_{c} }}{\partial t} \cdot \varvec{v} + 2\nu {\mathbb{D}}\left( {\varvec{u}_{c} } \right):{\mathbb{D}}\left( \varvec{v} \right) - p\nabla \cdot \varvec{v}} \right)d\Omega $$

(9c)

$$ + \eta \mathop \smallint \nolimits_{{\Gamma _{cd} }} \left( {\frac{1}{\rho }p_{f} \varvec{v} \cdot \varvec{n}_{cd} + \frac{\alpha \nu \sqrt N }{{\sqrt {{\text{trace}}\left( {\varvec{\Pi}} \right)} }}{\mathbb{P}}_{\tau } \left( {\varvec{u}_{c} + \frac{{k_{f} }}{\mu }\nabla p_{f} } \right) \cdot \varvec{v}} \right)d\Gamma $$

(9d)

$$ + \eta \mathop \smallint \nolimits_{{\Omega _{c} }} \nabla \cdot \varvec{u}_{c} qd\Omega - \mathop \smallint \nolimits_{{\Gamma _{cd} }} \varvec{u}_{c} \cdot \varvec{n}_{cd} \psi_{f} d\Gamma $$

(9e)

$$ = \eta \mathop \smallint \nolimits_{{\Omega _{c} }} \varvec{f} \cdot \varvec{v}d\Omega + \mathop \smallint \nolimits_{{\Omega _{d} }} q_{p} \psi_{f} d\Omega . $$

(9f)

$\eta$ is a scale factor applied to equations in the conduit subdomain to ensure the whole system is of the same scale.

3 Implementation

Hou et al. [15] numerically solved such a system in 2D using a finite element method with Taylor-Hood elements for the conduit domain and demonstrated the stability and convergence rate of their method.

In this section we describe an implementation of a finite element solver based on FEniCS [23, 24], which allows us to run our model in both 2D and 3D, in parallel, and can be easily modified and extended. FEniCS is a popular open source computing platform for solving partial differential equations (PDEs). The automatic code generation of FEniCS enables people to implement a FEM code using the Unified Form Language (UFL) [25], which is close to a mathematical description of the variational form.

Many multi-physics models have been implemented using FEniCS, e.g., the adaptive continuum mechanics solver Unicorn (Unified Continuum modeling) [26, 27]. It can solve continuum mechanics with moving meshes adaptively. As the coupled systems Unicorn solves always consist of moving meshes, subsystems are solved independently and iteratively until a satisfied error is reached. In our case, we prefer to solve the coupled system as a whole as they together form a linear system and can be solved directly.

A solution to the coupled Navier-Stokes-Darcy model has been implemented with FEniCS by Ida Norderhaug Drøsdal [28]. In the coupled Navier-Stokes-Darcy model, the conduit subdomain and the porosity subdomain contain the same two variables: fluid velocity and pressure. The solver regards the two subsystems as a whole and the variables exist on both subdomains. The interface conditions then are implemented by interior facet integration. However, in our coupled Stokes-Dual-Porosity model, we have two scalar variables $p_{f}$ and $p_{m}$ in the dual-porosity domain, but one vector variable $\varvec{u}_{c}$ and one scalar variable $p$ in the conduit domain.

The disagreement of the variable dimensions on the two subdomains differentiates our model from Navier-Stokes-Darcy model. Here we expand every variable to the whole system and force them to be zero in the opposite subdomain.

3.1 Implementation with FEniCS

Our implementation in Python is described in this section. Since our model involves interior interface integration, adjacent cells need to share information from the common facet. In order for our implementation to run in parallel, the following parameter in FEniCS needs to be set correctly.

For any given mesh object mesh, with any geometric dimension, our function space can be created as:

The four ordered elements selem , selem , velem , pelem in the last statement are for $p_{f}$, $p_{m}$, $\varvec{u}_{c}$ and $p$ respectively. Note that since the Taylor-Hood method is applied, the degree of $p$ should be less than that of $\varvec{u}_{c}$.

Initiate constants phim $= \varphi_{m}$, phif $= \varphi f$, km $= k_{m}$, kf $= k_{f}$, mu $= \mu$, nu $= \nu$, rho $= \rho$, sigma $= \sigma$, Cmt $= C_{mt}$, Cft $= C_{ft}$, alpha $= \alpha$, and eta $= \eta$, and function expressions qp $= q_{p}$ and f $= \varvec{f}$. Also define initial conditions for all variables, interpolated into our function space V, and stored in the variable x0 . The variational form can be defined in UFL as below. Note the one-to-one correspondence between the variational form below and the one presented in (9a)–(9f).

Note that the backward Euler scheme can be easily extended to $\theta$ method. dC , dD and dI are predefined Measure objects in UFL, and represents integrations on $\Omega _{c}$, $\Omega _{d}$ and $\Gamma _{cd}$ respectively. Note that the sign in needs to be adjusted for different domain structures. The signs of other variables for interface integration terms are not affecting the result of the model in any of our test cases.

Now we constrain $p_{m}$, $p_{f}$, $\varvec{u}_{c}$, $p$ on opposite subdomains by defining the following Dirichlet boundary conditions.

The boundary markers on_conduit/dual_but_not_interface , as their names might suggest, should not include the interface $\Gamma _{cd}$. Note that we need to use the method “pointwise” for these special “boundary” conditions.

After creating other Dirichlet boundary conditions bcs , we can solve the PDE as follows.

Due to the interface conditions our matrix $A$ is nonsymmetric. Hence, methods like conjugate gradients and Cholesky decomposition might not work as expected.

4 Result

The implementation works in 2D and 3D with the same code. Here we test our implementation on a unit cubic mesh defined by $\Omega = \left[ {0, 1} \right] \times \left[ {0, 1} \right] \times \left[ {0, 1} \right]$. Let $\Omega _{d} = \left\{ {\left( {x,y,z} \right) \in\Omega \left| {x \le y} \right.} \right\},\Omega _{c} = \left\{ {\left( {x,y,z} \right) \in\Omega \left| \;{x \ge y} \right.} \right\}$. We simulate our model on the time interval $\left[ {0,1} \right]$.

For the constants, we let $k_{m} = 0.1$ and all the rest be 1. We set up our coefficients and essential boundary conditions so that the following is our solution:

$$ p_{m} = \frac{1}{5}\sin \left( {x + y + z} \right)\cos \left( {\pi t} \right) $$

$$ p_{f} = - 2\pi \,\sin \left( {\pi t} \right)\,\sin \left( {x + y + z} \right) + \frac{4}{5}\sin \left( {x + y + z} \right)\cos \left( {\pi t} \right) $$

$$ \varvec{u}_{c} = \left[ {\begin{array}{*{20}c} {2\pi \,\sin \left( {\pi t} \right)\cos \left( {3x - y + z} \right) - \frac{4}{5}\cos \left( {\pi t} \right)\cos \left( {3y - x + z} \right)} \\ {2\pi \,\sin \left( {\pi t} \right)\cos \left( {3y - x + z} \right) - \frac{4}{5}\cos \left( {\pi t} \right)\cos \left( {3x - y + z} \right)} \\ {2\pi \,\sin \left( {\pi t} \right)\cos \left( {x + y + z} \right) - \frac{4}{5}\cos \left( {\pi t} \right)\cos \left( {x + y + z} \right)} \\ \end{array} } \right] $$

$$ \begin{aligned} p & = - 8\left( {\pi \,\sin \left( {\pi t} \right) + \frac{2}{5}\cos \left( {\pi t} \right)} \right)\left( {\sin \left( {3y - x + z} \right) \,+ \sin \left( {3x - y + z} \right)} \right) \\ & \quad +\, 2\left( {\frac{2}{5}\cos \left( {\pi t} \right) - \pi \,\sin \left( {\pi t} \right)} \right){ \sin }\left( {x + y + z} \right) \\ \end{aligned} $$

It is not hard to verify that the above solution satisfies Eq. (1) and (5)–(8). Source terms $q_{p}$ and $\varvec{f}$ can be calculated from (2) and (3) respectively. However, the divergence of the free flow velocity $\varvec{u}_{c}$ is not zero, so we need to modify (4) to a more general case $\nabla \cdot \varvec{u}_{c} = g$, and calculate $g$ from it.

For the boundary conditions, we apply corresponding essential boundaries for all variables except for $p$.

We tested our implementation on the University of Wyoming’s Teton HPC cluster [29].

4.1 Convergence

We examine the convergence rate of our implementation for different timestep length $\Delta t$’s. To make the result reproducible, all of the experiments are run in a single processor with the direct linear solver MUMPS (Multifrontal Massively Parallel sparse direct Solver) [30, 31]. Piecewise quadratic functions are used for $p_{m}$, $p_{f}$, and $\varvec{u}_{c}$. Degree 1 Lagrange elements are used for p.

We examine the convergence rate for both $\Delta t = h$ and $\Delta t = h^{2}$, where $h$ is the cell size. Recall that our domain is a unit cube. A model with cell size $h$ means our domain is partitioned into $h \times h \times h$ small cubes. Each cube contains 6 tetrahedral cells. The $L^{2}$ norm of each variable’s error at time $T = 1$ is calculated. The convergence rate is calculated as ${ \ln }\left( {e_{i} /e_{i - 1} } \right)/{ \ln }\left( {h_{i} /h_{i - 1} } \right)$. The result is shown in Tables 1 and 2.

Table 1. The $L^{2}$ error at $T = 1$ with $\Delta t = h$.

Table 2. The $L^{2}$ error at $T = 1$ with $\Delta t = h^{2}$.

4.2 Performance

The solver consists of two major parts: linear system assembling and linear system solving. Below we investigate the performance of our implementation in these two parts separately.

Assembling.

Despite that the linear form $L$ is assembled at each time step, the assembling of the bilinear form $a$ is usually more time consuming. Figures 2 and 3 show the time spent for assembling the bilinear form under different conditions.

Fig. 2.

Assembling time is linear to DoF.

Fig. 3.

Assembling scales well in large systems.

Figure 2 shows the assembling time when using a single CPU versus degrees of freedom (DoF) of our system. We can see that the assembling time is linear to total DoF.

Figure 3 presents the performance of assembling along different number of processors. Each line presents the scalability with fixed problem size. We can see that assembling scales well when the problem size is large enough. However, too many processors may lead to a performance drop.

Solving.

For our time-dependent model, the same linear system is solved at each timestep with varying right hand side. In this case, direct linear solvers can benefit from reuse of decompositions, as we will see in Figs. 4 and 5.

Fig. 4.

Time for solving a single step.

Fig. 5.

Time for solving 100 steps.

A collection of high performance solvers and preconditioners are available (callable) from FEniCS, assuming it was built with corresponding packages. To reduce complexity, we choose the ILU preconditioner hypre_euclid from Livermore’s HYPRE package [32] for all iterative solvers we use.

For a single solve, direct solvers like MUMPS and superlu_dist (Supernodal LU [33, 34]) is slower than iterative solvers, as shown in Fig. 4. But if we simulate for 100 steps, the direct solver MUMPS can overpass iterative solvers in not too large systems.

However, we can see in both figures, superlu_dist suffers from scalability. For large systems, a direct solver can still be slower and is much more memory consuming.

Memory Usage.

Figures 6 and 7 present the memory usages of our model under different situations. All memory usages are measured as the “Resident Set Size” of running processes. The memory usage is measured by the Resident Set Size used when running a simulation for $\Delta t = 0.01, t \in \left[ {0,1} \right]$, with specific solver. Note that the memory usage for iterative solvers are very similar: all their lines are overlapped with each other and some becomes invisible.

Fig. 6.

Memory usage versus degrees of freedom.

Fig. 7.

Memory usage versus number of processors.

For large systems, the memory usages of iterative solvers are about linear with respect to DoF and are worse than linear for direct solvers. In the case of $h = 1/32$, the total memory usage of a system with superlu_dist is about 7 times as large as that of a system with an iterative solver, as shown in Fig. 6.

Figure 7 shows how memory usage scales if we add more processors. The memory usage is the memory used by a single processor.

5 Conclusions and Future Work

We have presented an implementation of a coupled dual-porosity-Stokes model using the automated FEM solver FEniCS. We proposed a solution to modeling the coupled interface by using FEniCS’ built-in interface integration and expanding variables to the whole domain. This approach enables us to simulate both 2D and 3D models in parallel with minimum coding. Future work will include adding data assimilation from active sensors and experimenting with different interface conditions to see better solutions can be computed. Another approach is to implement one of the non-iterative domain decomposition methods that have been developed for Stokes-Darcy systems [35, 36], which can decompose our asymmetric matrix into two small symmetric matrices and reduce communications between two subsystems.