Abstract
Mathematical logic provides a formal language to describe complex abstract phenomena whereby a finite formula written in a finite alphabet states a property of an object that may even be infinite. Thus, the complexity of the underlying objects is abstracted away to give way for a simple syntactic description, a kind of mathesis universalis. The complexity, however, continues affecting which ways of reasoning are valid.
Structural proof theory reasons using proof objects more complex than individual formulas. One of its goals is to find minimal additional structures, depending on the complexity of the underlying objects, sufficient for efficient and modular reasoning about them.
In this paper, we are primarily interested in both the global structure used for reasoning and the local part of this structure employed to justify single inference steps. We provide recently developed examples where adapting the global structure of the sequent to the local structure of (potentially infinite) Kripke models yielded both quantitative and qualitative benefits in establishing fundamental logical properties such as complexity and interpolation.
The author is funded by FWF projects S 11405 (RiSE) and Y 544-N23.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Needless to say, this is not a cultist dogma claiming all logics to have analytic descriptions. Exceptions are made for degenerate logics, for monstrosities artificially created to defy proof-theoretic analysis, and for logics involving objectively complex notions, e.g., fixpoints (though the latter are still pursued and not entirely without success, cf., e.g., a recent survey of proof systems for common knowledge by Marti and Studer 2018). But an idea that adding one axiom may rob a logic of its cut-free representation is often met with disbelief and resistance.
- 2.
Which is almost inevitably interpreted to be cut-free.
- 3.
Bibliographic note: These two articles constituted Gentzen’s dissertation and were originally published in separate Hefte (issues) of Mathematische Zeitschrift in German. Their translation into English, combined into one article as originally intended, can be found in Gentzen (1969).
- 4.
Exceptions such as Gentzen’s sequents for intuitionistic logic only prove the rule.
- 5.
A preorder is a reflexive and transitive binary relation.
- 6.
According to a private communication with Melvin Fitting, at the time he did not know of Maehara’s results, which were published in German. In fact, I had the pleasure of translating them for him to confirm the connection as recently as in 2015. Given that Beth did not reference Maehara either, it is likely that the two systems have been developed independently, which often happens with fruitful ideas in proof theory.
- 7.
Some intuitionistic semantics insist on the proof of a disjunction having to carry information about which disjunct was proved, but the official BHK interpretation does not (see Moschovakis 2015).
- 8.
An intermediate logic is a logic between Int and classical propositional logic.
- 9.
Alternatively, Fitting suggested working in a language without implication, where formulas never reach the other side of the sequent arrow ⇒. He called such sequent systems symmetric (Fitting 1983). However, the symmetric option is only available for classical-based logics since implication is not definable through other connectives intuitionistically.
- 10.
The symbol \(\mho \) is used as a unit in physics. Due to its reciprocal connection to ohm, denoted Ω, the symbol \(\mho \) represents an upside down Ω and its pronunciation, mho is the word ohm read backwards.
- 11.
The polarity of p occurring in \(\overline {E}\mathstrut ^{(k)}\) (in E (k)) is opposite to (the same as) the polarity of p in E. The operations
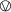 and
and 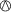 preserve polarity.
preserve polarity. - 12.
We apply the term principle to components of a hypersequent by analogy with its usage for formulas: a principle component is the one in the succedent of the rule, to which the rule is applied, i.e., the one without which this rule would not have been applicable.
- 13.
References
Avron, A. (1987). A constructive analysis of RM. Journal of Symbolic Logic, 52(4), 939–951. https://doi.org/10.2307/2273828.
Avron, A. (1996). The method of hypersequents in the proof theory of propositional non-classical logics. In W. Hodges, M. Hyland, C. Steinhorn, & J. Truss (Eds.), Logic: From Foundations to Applications: European Logic Colloquium (pp. 1–32). Clarendon Press.
Baaz, M., Ciabattoni, A., & Fermüller, C. G. (2003). Hypersequent calculi for Gödel logics—a survey. Journal of Logic and Computation, 13(6), 835–861. https://doi.org/10.1093/logcom/13.6.835.
Brünnler, K. (2006). Deep sequent systems for modal logic. In G. Governatori, I. Hodkinson, & Y. Venema (Eds.), (Advances in Modal Logic, Vol. 6, pp. 107–119). College Publications. Available from: http://www.aiml.net/volumes/volume6/Bruennler.ps.
Brünnler, K. (2010). Nested sequents. Habilitation thesis, Institut für Informatik und angewandte Mathematik, Universität Bern, Apr 2010. Available from: https://arxiv.org/abs/1004.1845.
Bull, R. A. (1992). Cut elimination for propositional dynamic logic without *. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 38, 85–100. https://doi.org/10.1002/malq.19920380107.
van Benthem, J. (2008). The many faces of interpolation. Synthese, 164(3), 451–460. https://doi.org/10.1007/s11229-008-9351-5.
Chagrov, A., & Zakharyaschev, M. (1997). Modal logic (Oxford logic guides, Vol. 35). Clarendon Press. Available from: https://global.oup.com/academic/product/modal-logic-9780198537793.
Ciabattoni, A., & Ferrari, M. (2001). Hypersequent calculi for some intermediate logics with bounded Kripke models. Journal of Logic and Computation, 11(2), 283–294. https://doi.org/10.1093/logcom/11.2.283.
Ciabattoni, A., Galatos, N., & Terui, K. (2008). From axioms to analytic rules in nonclassical logics. In Proceedings, Twenty-Third Annual IEEE Symposium on Logic in Computer Science (pp. 229–240). IEEE. https://doi.org/10.1109/LICS.2008.39.
Craig, W. (1957a). Linear reasoning. A new form of the Herbrand–Gentzen theorem. Journal of Symbolic Logic, 22(3), 250–268. https://doi.org/10.2307/2963593.
Craig, W. (1957b). Three uses of the Herbrand–Gentzen Theorem in relating model theory and proof theory. Journal of Symbolic Logic, 22(3), 269–285. https://doi.org/10.2307/2963594.
Dyckhoff, R., & Negri, S. (2012). Proof analysis in intermediate logics. Archive for Mathematical Logic, 51(1–2), 71–92. https://doi.org/10.1007/s00153-011-0254-7.
Fitting, M. (1972). Tableau methods of proof for modal logics. Notre Dame Journal of Formal Logic, XIII(2), 237–247. https://doi.org/10.1305/ndjfl/1093894722.
Fitting, M. (1983). Proof methods for modal and intuitionistic logics. Synthese library (Vol. 169). D. Reidel Publishing Company. https://doi.org/10.1007/978-94-017-2794-5.
Fitting, M. (2012). Prefixed tableaus and nested sequents. Annals of Pure and Applied Logic, 163(3), 291–313. https://doi.org/10.1016/j.apal.2011.09.004.
Fitting, M. (2014). Nested sequents for intuitionistic logics. Notre Dame Journal of Formal Logic, 55(1), 41–61. https://doi.org/10.1215/00294527-2377869.
Fitting, M., & Kuznets, R. (2015). Modal interpolation via nested sequents. Annals of Pure and Applied Logic, 166(3), 274–305. https://doi.org/10.1016/j.apal.2014.11.002.
Gabbay, D. M. (1993). Labelled deductive systems: A position paper. In J. Oikkonen & J. Väänänen (Eds.), Logic Colloquium’90 (Lecture notes in logic, Vol. 2, pp. 66–88). Springer. https://doi.org/10.1017/9781316718254.008.
Gabbay, D. M. (1996). Labelled deductive systems, volume 1 (Oxford logic guides, Vol. 33). Oxford: Clarendon Press.
Gabbay, D. M., & Maksimova, L. (2005). Interpolation and definability: Modal and intuitionistic logics (Oxford logic guides, Vol. 46). Clarendon Press. https://doi.org/10.1093/acprof:oso/9780198511748.001.0001.
Gentzen, G. (1935a). Untersuchungen über das logische Schließen. I. Mathematische Zeitschrift, 39, 176–210. In German. https://doi.org/10.1007/BF01201353.
Gentzen, G. (1935b). Untersuchungen über das logische Schließen. II. Mathematische Zeitschrift, 39, 405–431. In German. https://doi.org/10.1007/BF01201363.
Gentzen, G. (1969). Investigations into logical deduction. In M. E. Szabo (Ed.), The Collected Papers of Gerhard Gentzen (Studies in logic and the foundations of mathematics, Vol. 55, pp. 68–131). North-Holland. Originally published in German in 1935. https://doi.org/10.1016/S0049-237X(08)70822-X.
Goré, R., & Ramanayake, R. (2012). Labelled tree sequents, tree hypersequents and nested (deep) sequents. In T. Bolander, T. Braüner, S. Ghilardi, & L. Moss (Eds.), Advances in Modal Logic (Vol. 9, pp. 279–299). College Publications. Available from: http://www.aiml.net/volumes/volume9/Gore-Ramanayake.pdf.
Jankov, V. A. (1968). The calculus of the weak “law of excluded middle”. Mathematics of the USSR–Izvestiya, 2(5), 997–1004. Originally published in Russian as Янков (1968). https://doi.org/10.1070/IM1968v002n05ABEH000690.
Kashima, R. (1994). Cut-free sequent calculi for some tense logics. Studia Logica, 53(1), 119–135. https://doi.org/10.1007/BF01053026.
Kuznets, R. (2016a). Craig interpolation via hypersequents. In D. Probst & P. Schuster (Eds.), Concepts of proof in mathematics, philosophy, and computer science (Ontos mathematical logic, Vol. 6, pp. 193–214). De Gruyter. https://doi.org/10.1515/9781501502620-012.
Kuznets, R. (2016b). Interpolation method for multicomponent sequent calculi. In S. Artemov & A. Nerode (Eds.), Logical Foundations of Computer Science, International Symposium, LFCS 2016, Deerfield Beach, 4–7 Jan 2016, Proceedings (LNCS, Vol. 9537, pp. 202–218). Springer. https://doi.org/10.1007/978-3-319-27683-0_15.
Kuznets, R. (2018). Multicomponent proof-theoretic method for proving interpolation property. Annals of Pure and Applied Logic, 169(12), 1369–1418. https://doi.org/10.1016/j.apal.2018.08.007.
Kuznets, R., & Lellmann, B. (2016). Grafting hypersequents onto nested sequents. Logic Journal of the IGPL, 24(3), 375–423. https://doi.org/10.1093/jigpal/jzw005.
Kuznets, R., & Lellmann, B. (2018). Interpolation for intermediate logics via hyper- and linear nested sequents. In G. Bezhanishvili, G. D’Agostino, G. Metcalfe, & T. Studer (Eds.), Advances in Modal Logic (Vol. 12, pp. 473–492). College Publications.
Kuznets, R., & Lellmann, B. (2018, Submitted). Interpolation for intermediate logics via injective nested sequents.
Lahav, O. (2013). From frame properties to hypersequent rules in modal logics. In Proceedings, 2013 28th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2013 (pp. 408–417). IEEE. https://doi.org/10.1109/LICS.2013.47.
Lellmann, B. (2015). Linear nested sequents, 2-sequents and hypersequents. In H. De Nivelle (Ed.), Analytic Reasoning with Analytic Tableaux and Related Methods, 24th International Conference, TABLEAUX 2015, Wrosław, Poland, 21–24 Sept 2015, Proceedings (LNAI, Vol. 9323, pp. 135–150). Springer. https://doi.org/10.1007/978-3-319-24312-2_10.
Lellmann, B. (2016). Hypersequent rules with restricted contexts for propositional modal logics. Theoretical Computer Science, 656(A), 76–105. https://doi.org/10.1016/j.tcs.2016.10.004.
Lyndon, R. C. (1959). An interpolation theorem in the predicate calculus. Pacific Journal of Mathematics, 9(1), 129–142. https://doi.org/10.2140/pjm.1959.9.129.
Maehara, S. (1954). Eine Darstellung der intuitionistischen Logik in der Klassischen. Nagoya Mathematical Journal, 7, 45–64. In German. https://doi.org/10.1017/S0027763000018055.
Maehara, S. (1961). On the interpolation theorem of Craig. Sugaku, 12(4), 235–237. In Japanese. https://doi.org/10.11429/sugaku1947.12.235.
Maksimova, L. L. (1982). The Lyndon interpolation theorem for modal logics. In Mathematical logic and algorithm theory. Trudy Instituta matematiki (Vol. 2, pp. 45–55). Sobolev Institute of Mathematics, Siberian Branch of the Russian Academy of Sciences. In Russian. Available from: http://math.nsc.ru/journals/ti/02/ti_02_0003.pdf.
Maksimova, L. L. (2014). The Lyndon property and uniform interplolation over the Grzegorczyk logic. Siberian Mathematical Journal, 55(1), 118–124. Originally published in Russian as Максимова (2014). https://doi.org/10.1134/S0037446614010145.
Marti, M., & Studer, T. (2018). The proof theory of common knowledge. In H. van Ditmarsch & G. Sandu (Eds.), Jaakko Hintikka on knowledge and game-theoretical semantics (Outstanding contributions to logic, Vol. 12, pp. 433–455). Springer. https://doi.org/10.1007/978-3-319-62864-6_18.
Masini, A. (1992). 2-sequent calculus: A proof theory of modalities. Annals of Pure and Applied Logic, 58(3), 229–246. https://doi.org/10.1016/0168-0072(92)90029-Y.
Massacci, F. (1994). Strongly analytic tableaux for normal modal logics. In A. Bundy (Ed.), Automated Deduction—CADE-12, 12th International Conference on Automated Deduction, Nancy, 26 June–1 July 1994, Proceedings (LNAI, Vol. 814, pp. 723–737). Springer. https://doi.org/10.1007/3-540-58156-1_52.
Minc, G. E. (1971). On some calculi of modal logic. In V. P. Orevkov (Ed.), The calculi of symbolic logic. I (Proceedings of the Steklov Institute of mathematics, Vol. 98(1968), pp. 97–124). AMS. Originally published in Russian in 1968 as Минц (1968). Available from: http://mi.mathnet.ru/eng/tm/v98/p88.
Mints, G. (1997). Indexed systems of sequents and cut-elimination. Journal of Philosophical Logic, 26(6), 671–696. https://doi.org/10.1023/A:1017948105274.
Moschovakis, J. (2015). Intuitionistic logic. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, Spring 2015 edition. Available from: http://plato.stanford.edu/archives/spr2015/entries/logic-intuitionistic/.
Negri, S. (2005). Proof analysis in modal logic. Journal of Philosophical Logic, 34(5–6), 507–544. https://doi.org/10.1007/s10992-005-2267-3.
Negri, S., & von Plato, J. (2011). Proof analysis: A contribution to Hilbert’s Last Problem. Cambridge University Press. https://doi.org/10.1017/CBO9781139003513.
Poggiolesi, F. (2008). Sequent calculi for modal logic. Ph.D. thesis, University of Florence.
Poggiolesi, F. (2011). Gentzen calculi for modal propositional logic (Trends in Logic, Vol. 32). Springer. https://doi.org/10.1007/978-90-481-9670-8.
Sato, M. (1977). A study of Kripke-type models for some modal logics by Gentzen’s sequential method. Publications of the Research Institute for Mathematical Sciences, Kyoto University, 13(2), 381–468. https://doi.org/10.2977/prims/1195189814.
Viganò, L. (2000). Labelled non-classical logics. Springer. https://doi.org/10.1007/978-1-4757-3208-5.
Максимова, Л. Л. (2014). Свойство Линдона и униформная интерполяция над логикой Гжегорчика. Сибирский математический журнал, 55(1), 147–155. Available from: http://mi.mathnet.ru/eng/smj2520.
Минц, Г. . (1968). О некоторых исчислениях модальной логики. In В. . Оревков (Ed.), Логические и логико-математические исчисления. I. Труды МИАН СССР (Vol. 98, pp. 88–111). Nauka. Available from: http://mi.mathnet.ru/tm2927.
Янков, В. А. (1968). Об исчислении слабого закона исключенного третьего. Известия Академии наук СССР, Серия математическая, 32(5), 1044–1051. Available from: http://mi.mathnet.ru/eng/izv2504.
Acknowledgements
I would like to thank Stefania Centrone, Sara Negri, Denis Sarikaya, and Peter Schuster for organizing the Kolleg, which brought together so many outstanding scientists from different communities and different generations that I remember often feeling an awe and inspiration in equal measure during talks and after-talk discussions. I thank Agata Ciabattoni for her continuous support. I am grateful for the anonymous reviewer for their words of encouragement. I am also deeply indebted to Melvin Fitting, who was kind enough to take a look at this paper and immediately saw how to improve it. I should also say this paper would not have happened without everything I had learned from him over the years.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Kuznets, R. (2019). Through an Inference Rule, Darkly. In: Centrone, S., Negri, S., Sarikaya, D., Schuster, P.M. (eds) Mathesis Universalis, Computability and Proof. Synthese Library, vol 412. Springer, Cham. https://doi.org/10.1007/978-3-030-20447-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-20447-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-20446-4
Online ISBN: 978-3-030-20447-1
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


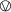 and
and 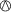 preserve polarity.
preserve polarity.