Abstract
This chapter examines the pioneering work of Gottfried Wilhelm Leibniz (1646–1716) on various number systems, in particular binary, which he independently invented in the mid-to-late 1670s, and hexadecimal, which he invented in 1679. The chapter begins with the oft-debated question of who may have influenced Leibniz’s invention of binary, though as none of the proposed candidates is plausible, I suggest a different hypothesis that Leibniz initially developed binary notation as a tool to assist his investigations in mathematical problems that were exercising him at the time, namely those concerning the divisibility of composite numbers, primality, and perfect numbers. The chapter then explores Leibniz’s development of binary, his little-known work on binary fractions and expansions, his use of binary as a symbol for creation in his philosophical-theology, and his response to the suggestion that there was a correlation between binary numeration and the hexagrams of the ancient Chinese divinatory text, the Yijing. The chapter then focuses on Leibniz’s work on other number systems, in particular his invention and exploration of hexadecimal as well as his work on duodecimal. The chapter concludes by revealing a hitherto unknown practical application of binary that Leibniz devised in the last year of his life.
Notes
- 1.
- 2.
In 1711, decades after devising binary and only 5 years before his death, Leibniz (1768, V: 418) wrote: “Regarding Caramuel’s Mathesis biceps [Old] and New, for which he asks ten thalers, I am unable to judge well because I have not yet seen it, and I fear it may contain vain subtleties, which is not unusual for Caramuel.”
- 3.
This work yielded his first publication in mathematics in February 1678, namely, the short journal article “A new observation about the way of testing whether a number is prime”; see Leibniz 1678/http://www.leibniz-translations.com/prime.htm. For details of Leibniz’s work on primes, see Mahnke (1912–1913).
- 4.
In the manuscript entitled “Formarum reductio ad simplices,” written 12 September 1680: “Therefore, 2z–1 – 1 will be divisible by z, if z is prime” (LH 35, 3 A 4 Bl. 14r). During these investigations, Leibniz also glimpsed Wilson’s theorem: (n – 2)! ≡ 1 (mod n), or in Leibniz’s words: “The product of continuous [integers] up to the number which anteprecedes the given integer, when divided by the given integer, leaves 1, if the given integer is prime. If the given integer is derivative, it will leave a number which, since it has a common measure with the given integer, is greater than one” (LH 35 3 B 11 Bl. 21r). However, when testing his articulation of the theorem, Leibniz made a miscalculation that led him to add the false statement “(or the complement of 1)” after “leaves 1.”
- 5.
In a slightly later manuscript, from 1679 (LH 35, 8, 30 Bl. 148), Leibniz again uses binary notation to illustrate his (still immature) formulation of a prime number theorem, namely, 2n – 1: “Let
 = 111111,
= 111111,  = 1111,
= 1111,  = 111,
= 111,  = 11.
= 11.  =
=  A,
A, 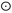 =
=  B. Now
B. Now  and
and  are prime among themselves, because their exponents are such, that is, their indices, or the numbers 2 and 3. Therefore A and B are not prime among themselves and necessarily will become A =
are prime among themselves, because their exponents are such, that is, their indices, or the numbers 2 and 3. Therefore A and B are not prime among themselves and necessarily will become A = 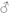 C and B =
C and B =  C, and will become
C, and will become  =
=  C. Zz – 1 is divisible by Z if Z is prime, and I have demonstrated this as follows: 22 – 1 by 3 and 24 – 1 by 5, therefore 1111 is divisible by 5 and 11 by 3 and 111111 by 7. But 11111 cannot be divided by 6, for since 11 can be divided by 3, 11111 and 11 have a common divisor, yet they are prime among themselves. And hence we have the sought-for demonstration of a reciprocal property of a prime number.”
C. Zz – 1 is divisible by Z if Z is prime, and I have demonstrated this as follows: 22 – 1 by 3 and 24 – 1 by 5, therefore 1111 is divisible by 5 and 11 by 3 and 111111 by 7. But 11111 cannot be divided by 6, for since 11 can be divided by 3, 11111 and 11 have a common divisor, yet they are prime among themselves. And hence we have the sought-for demonstration of a reciprocal property of a prime number.” - 6.
Euclid, Elements, IX.36. That is, if p is a positive integer and 2p – 1 is prime, then 2p-1 (2p − 1) is perfect.
- 7.
Perhaps because of this, in another manuscript on the subject, probably written in 1678, Leibniz sought to demonstrate perfect numbers using a mixture of binary numeration and algebra based thereon (so unrelated to Pauli’s algebra), eventually reaching the conclusion “22z+1 – 2z will be a perfect number if 2z+1 – 1 is prime. Likewise, 2z–1 – 1 will be divisible by z, if z is prime” (LH 35, 3 B 17 Bl. 1).
- 8.
Leibniz explicitly acknowledged these features, at least in the 1680s onward. For example: “The very last digits of a number of the double geometric progression can be easily obtained like this: if 1 is subtracted from it, then it is written in binary: etc.1111111, that is, 1 + 2 + 4 + 8 + 16 + 32 etc.” (LH 35, 3 B 11 Bl. 10r; cf. LH 35, 8, 30 Bl. 75; LH 35, 13, 3 Bl. 33; LH 35, 15, 5 Bl. 10r; and LH 35, 3 B 5 Bl. 51r).
- 9.
A similar table is found in other manuscripts, such as LH 35, 4, 11 Bl. 10r, though this was likely written in 1681.
- 10.
Another writing in this vein is printed in Strickland and Lewis (2022, 41–43).
- 11.
Leibniz did not affix a date to them, and the paper contains no watermarks that could be used to determine a dating, so they have to be dated using internal evidence.
- 12.
Leibniz also refers to “the binary progression, where only ones and 0 express a number,” in a manuscript on the construction of a universal language, tentatively dated to February 1678 (A VI 4, 68).
- 13.
A third is outlined in Strickland and Lewis (2022, 40n2).
- 14.
Although in one early writing he exclaims that binary will be “remarkable for periodic progressions in expressible quantities which are not whole or rational” (Strickland and Lewis 2022, 32).
- 15.
For further details of Leibniz’s work on the binary expression of his circle formula, see Strickland (2023a).
- 16.
- 17.
Or as he puts it in a manuscript written perhaps in 1695 or possibly in 1702, “things are educed from God’s active power—as Julius Scaliger said—rather than from passive nothing. My invention of the composition of numbers from 0 and 1 would wonderfully support this doctrine” (LH 4, 3, 5e Bl. 5). See Scaliger (1557, fols. 16–17).
- 18.
When Leibniz did come to write the Theodicy more than a decade later, the binary-creation analogy was not mentioned. The Theodicy was published in 1710. See Leibniz (1985).
- 19.
There are other sequences of hexagrams apart from the two mentioned already, such as the Eight Palaces sequence, which predates the Fuxi sequence. These sequences have elicited many studies of their structure, interrelation, and history, though such matters are outside of the scope of this chapter.
- 20.
For more information on Bouvet’s hypothesis and Leibniz’s reaction thereto, see Kempe (2022, 141–174).
- 21.
For more information about the history of base 16, and Leibniz’s place therein, see Strickland and Jones (2023).
- 22.
The same conversion of 100000 to 186u016 is also found in a contemporaneous text: LH 35, 8, 30 Bl. 148r.
- 23.
Leibniz is probably thinking of Schwenter’s Deliciae physico-mathematicae [The Charms of Physico-Mathematics] of 1636, which was posthumously revised and expanded by Georg Philipp Harsdörffer (1607–1658) in 1651 and again in 1653. However, as far as I have been able to tell, in none of those works is there any mention of duodecimal, let alone any report of anyone endorsing it.
- 24.
Leibniz actually wrote “1728,” but this is clearly a mistake as his example uses 1712.
- 25.
After this example, Leibniz turned to the quaternary system, efficiently sketching out the steps required to convert the decimal value 1712 to 1223004 (LBr 705 Bl. 93r). He then did the same with binary, before turning to the periodicity of columns in binary.
- 26.
For further details of Leibniz’s tactile binary clock, and an English translation of the manuscript, see Strickland (2023b).
- 27.
Leibniz himself had devised a spring-driven pocket watch in the mid-1670s and continued to improve it even four decades later; see Leibniz 1675, and LH 38 Bl. 274–275.
Bibliography
Bacon F (1623) De dignitate et augmentis scientiarum, libri IX. Haviland, London
Caramuel y Lobkowitz, Juan (1670) Mathesis biceps, vetus et nova. Annison, Campagna
Couturat L (1901) La logique de Leibniz. Félix Alcan, Paris
Dangicourt P (1710) De periodis columnarum in serie numerorum progressionis arithmeticae dyadice expressorum. Miscellanea Berolinensia 1:336–376
Glaser A (1981) History of binary and other nondecimal numeration, 2nd edn. Tomash, Los Angeles
Harsdörffer GP (1651) Delitiae mathematicae et physicae der Mathematischen und Philosophischen Erquickstunden. Zweiter Theil. Dümler, Nuremberg
Harsdörffer GP (1653) Delitiae mathematicae et physicae der Mathematischen und Philosophischen Erquickstunden. Dritter Theil. Endters, Nuremberg
Hill TW (1860) Selections from the papers of the Late Thomas Wright Hill, Esq. F.R.A.S. John W. Parker and Son, London
Hochstetter E (1966) Herrn von Leibniz’ Rechnung mit Null und Eins. Siemens, Berlin
Ineichen R (2008) Leibniz, Caramuel, Harriot und das Dualsystem. Mitteilungen der deutschen Mathematiker-Vereinigung 16(1):12–15
Ingaliso L (2017) Leibniz e la lettura binaria dell’I Ching. In: Lio GMS, Ingaliso L (eds) Alterità e Cosmopolitismo nel Pensiero Moderno e Contemporaneo. Rubbettino, Soveria Mannelli, pp 109–132
Intorcetta, Prospero, ChristianWolfgang Herdtrick, François de Rougemont, Philippe Couplet, eds. and trans. (1687) Confucius Sinarum philosophus. Daniel Horthemels, Paris.
Jordaine J (1687) Duodecimal arithmetick. John Richardson, London
Kempe M (2022) Die beste aller möglichen Welten: Gottfried Wilhelm Leibniz in seiner Zeit. S. Fischer, Frankfurt
Knobloch E (2018) Determinant theory, symmetric functions, and dyadic. In: Antognazza MR (ed) The Oxford handbook of Leibniz. Oxford University Press, Oxford, pp 225–246
Knuth DE (1983) History of binary and other nondecimal numeration. By Anton Glaser. Los Angeles, CA (Tomash Publishers). 1981. 218 + xiii pp.” Historia Mathematica 10: 236–243.
Knuth DE (1998) The art of computer programming. Volume 2: Seminumerical algorithms, 3rd edn. Addison–Wesley, Upper Saddle River
Kolpas S (2019) Napier’s Binary chessboard calculator. Math Horiz 27:25–27
LBr = Manuscript held by Gottfried Wilhelm Leibniz Bibliothek – Niedersächsische Landesbibliothek, Hanover, Germany. Cited by shelfmark and Blatt [sheet]
Leibniz GW (1675) Extrait d’une lettre de Mr. Leibniz à l’auteur du journal, touchant le principe de justesse des horloges portatives de son invention. J des sçavans:93–96
Leibniz GW (1678) Extrait d’une lettre ecrite d’Hanovre par M. de Leibniz à l’Auteur du Journal, contenant une observation nouvelle de la maniere d’essayer si un nombre est primitif. J des sçavans:75–76
Leibniz GW (1768) Opera Omnia. Edited by Louis Dutens. 6 vols. Fratres de Tournes, Geneva
Leibniz GW. (1849–1863) Leibniziens Mathematische Schriften. Edited by C. I. Gerhardt. 7 vols. H. W. Schmidt, Halle
Leibniz GW (1923–.) Sämtliche Schriften und Briefe. Edited by Berlin-Brandenburgische Akademie der Wissenschaften. 8 series, each divided into multiple volumes. Akademie Verlag, Berlin
Leibniz GW (1969) Philosophical papers and letters, ed. and trans. Leroy E. Loemker. D. Reidel, Dordrecht
Leibniz GW (1971) Calcolo con zero e uno. Translated by Lia Ruffino. Etas Kompass, Milan
Leibniz GW (1985) Theodicy. Translated by E. M. Huggard. Open Court, Chicago
Leibniz GW (2006) Shorter Leibniz texts. Edited and translated by Lloyd Strickland. Continuum, London
LH = Manuscript held by Gottfried Wilhelm Leibniz Bibliothek – Niedersächsische Landesbibliothek, Hanover, Germany. Cited by shelfmark and Blatt [sheet]
Mahnke, Dietrich. 1912–13. Leibniz auf der Suche nach einer allgemeinen Primzahlgleichung,” Bibliotheca Math. 13:29–61.
Mersenne M (1644) Cogitata physico mathematica. In quibus naturae quam artis effectus admirandi certissimis demonstrationibus explicantur. Bertier, Paris
Morley FV (1922) Thomas Hariot—1560–1621. Sci Mon 14(1):60–66
Napier J (1617) Rabdologiæ. Andreas Hart, Edinburgh
Nystrom JW (1862) Project of a new system of arithmetic, weight, measure and coins, proposed to be called the tonal system, with sixteen to the base. J. B. Lippincott & Co, Philadelphia
Nystrom JW (1863) On a new system of arithmetic and metrology, called the tonal system. J Franklin Institute 76:263–275, 337–348, 402–407
Pascal B (1665) Traité du triangle arithmetique, avec quelques autres petits traitez sur la mesme materiere. Guillaume Desprez, Paris
Pauli JW (1678) Disputatione mathematica numerum perfectum perfectissimi. Georg, Leipzig
Ramus P (1599) Arithmetica et geometria. Claude Marnium and Johannes Aubrium, Frankfurt
Riese A (1529) Rechnung auff der Linihen und Federn, n.p., Erfurt
Scaliger, JC (1557) Exotericarum exercitationum liber quintus decimus, de subtilitate, ad Hieronymum Cardanum. Michael Vasocsani, Paris
Schott G (1658) Magia universalis naturae & artis. Operis quadripartiti. Tomus tertius & quartus. Johann Gottfried Schönwetter, Frankfurt
Schwenter D (1636) Deliciae physico-mathematicae oder Mathematische und philosophische Erquickstunden. Dümmler, Nuremberg
Serra Y (2010a) Le manuscrit «De Progressione Dyadica» de Leibniz. http://www.bibnum.education.fr/sites/default/files/leibniz-analyse.pdf
Serra Y (2010b) Traduction du fac-similé du manuscrit de Leibniz du 15 mars 1679, «De Progressione Dyadica». http://www.bibnum.education.fr/sites/default/files/leibniz-numeration-texte.pdf
Stein E, Kopp FO, Wiechmann K, Weber G (2006) Neue Forschungsergebnisse und Nachbauten zur Vier-Spezies- Rechenmaschine und zur Dyadischen Rechenmaschine nach Leibniz. In: VIII. Internat. Leibniz-Kongress, Vorträge 2. Teil, 1018–1025. Hannover
Stifel M (1544) Arithmetica integra. Johan. Petreium, Nuremberg
Strickland L (2014) Leibniz’s monadology: a new translation and guide. Edinburgh University Press, Edinburgh
Strickland, L (2022) An unpublished manuscript of Leibniz’s on duodecimal. The Duodecimal Bulletin 54: 20z–26z
Strickland L (2023a) How Leibniz tried to tell the world he had squared the circle. Hist Math 62:19–39. https://doi.org/10.1016/j.hm.2022.08.004
Strickland L (2023b) Leibniz’s tactile binary clock. L.I.S.A. Wissenschaftsportal Gerda Henkel Stiftung. https://lisa.gerda-henkel-stiftung.de/leibnitzstactileclock
Strickland L (2023c) Why did Thomas Harriot invent binary? Math Intell. https://link.springer.com/article/10.1007/s00283-023-10271-9
Strickland L, Jones OD (2023) F things you (probably) didn’t know about hexadecimal. Math Intell. https://doi.org/10.1007/s00283-022-10206-w
Strickland L, Lewis H (2022) Leibniz on binary: the invention of computer arithmetic. MIT Press, Cambridge, MA
Swetz, Frank J. 2003. Leibniz, the Yijing, and the Religious conversion of the Chinese. Math Mag 76 (4): 276–291.
Sypniewski, Bernard Paul. 2005. China and universals: Leibniz, binary mathematics, and the Yijing Hexagrams Monumenta Serica 53:287–314.
Tropfke J (1980) Geschichte der Elementarmathematik. Band 1: Arithmetik und Algebra, 4th edn. De Gruyter, Berlin
von Mackensen L (1974) Leibniz als Ahnherr der Kybernetik—ein bisher unbekannter Leibnizscher Vorschlag einer ‘Machina arithmeticae dyadicae’. In: Akten des II Internationalen Leibniz-Kongresses, II:255–268. Steiner Verlag, Wiesbaden
Weigel E (1673) Tetractys, Summum tum Arithmeticae tum Philosophiae discursivae compendium, artis magnae sciendi. Meyer, Jena
Zacher HJ (ed) (1973) Die Hauptschriften zur Dyadik von G. W. Leibniz. Vittorio Klostermann, Frankfurt
Zhonglian S (2000) Leibniz’s binary system and Shao Yong’s Xiantiantu. In: Li W, Poser H (eds) Das Neueste über China: G.W. Leibnizens Novissima Sinica von 1697. Franz Steiner Verlag, Stuttgart, pp 165–169
Acknowledgments
The author would like to express his gratitude to the Gerda Henkel Stiftung, Düsseldorf, for their award of a research scholarship (AZ 46/V/21), which made this chapter possible. The author would also like to thank Daniel J. Cook, Donald E. Knuth, and Harry R. Lewis for their helpful comments on an earlier version of this chapter; Siegmund Probst and Julia Weckend for their assistance in transcribing manuscripts and their illuminating discussion thereof; and Lisa Silva – @lisa_cs8 – for her illustration of Leibniz’s tactile clock.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Section Editor information
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this entry
Cite this entry
Strickland, L. (2022). Leibniz on Number Systems. In: Sriraman, B. (eds) Handbook of the History and Philosophy of Mathematical Practice. Springer, Cham. https://doi.org/10.1007/978-3-030-19071-2_90-1
Download citation
DOI: https://doi.org/10.1007/978-3-030-19071-2_90-1
Received:
Accepted:
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-19071-2
Online ISBN: 978-3-030-19071-2
eBook Packages: Springer Reference MathematicsReference Module Computer Science and Engineering


 = 111111,
= 111111,  = 1111,
= 1111,  = 111,
= 111,  = 11.
= 11.  =
=  A,
A, 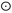 =
=  B. Now
B. Now  and
and  are prime among themselves, because their exponents are such, that is, their indices, or the numbers 2 and 3. Therefore A and B are not prime among themselves and necessarily will become A =
are prime among themselves, because their exponents are such, that is, their indices, or the numbers 2 and 3. Therefore A and B are not prime among themselves and necessarily will become A = 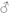 C and B =
C and B =  C, and will become
C, and will become  =
=  C. Zz – 1 is divisible by Z if Z is prime, and I have demonstrated this as follows: 22 – 1 by 3 and 24 – 1 by 5, therefore 1111 is divisible by 5 and 11 by 3 and 111111 by 7. But 11111 cannot be divided by 6, for since 11 can be divided by 3, 11111 and 11 have a common divisor, yet they are prime among themselves. And hence we have the sought-for demonstration of a reciprocal property of a prime number.”
C. Zz – 1 is divisible by Z if Z is prime, and I have demonstrated this as follows: 22 – 1 by 3 and 24 – 1 by 5, therefore 1111 is divisible by 5 and 11 by 3 and 111111 by 7. But 11111 cannot be divided by 6, for since 11 can be divided by 3, 11111 and 11 have a common divisor, yet they are prime among themselves. And hence we have the sought-for demonstration of a reciprocal property of a prime number.”