Convex and Concave Vertices on a Simple Closed Curve in the Triangular Grid

Abstract

We propose a classification of convex and concave vertices on a simple closed curve in the triangular grid into two types, based on the angle turn the curve makes at the vertex. We prove a combinatorial property for the number of convex and concave vertices of different types.

1 Introduction

There are three regular grids in the plane, inducing the tiling of the plane into regular triangles, squares or hexagons, called collectively pixels. Although the square grid received the most attention in the literature, the two alternative grids were also widely investigated in different frameworks, such as topology-preserving transformations [14, 15, 21, 24, 25, 34], computation of the Euler characteristic [4, 22, 33], analytical [1, 5, 16, 20, 30] or computational [31, 32] geometry, tomography [29], topological/combinatorial coordinate systems [23, 28], distance transform [2, 3] and neighborhood sequences [17], to name just a few.

Chain codes were designed to represent digital curves composed of pixels in the square grid, by specifying the direction in which the next pixel on the curve lies. They were extended to vertex chain codes [4], to represent one-dimensional interpixel boundaries of well-composed [27] binary objects, i.e., simple closed curves composed of grid edges. Vertex chain codes were defined in all three regular grids. The code of a vertex is equal to the number of interior (black or object) pixels incident to the vertex.

In the square grid, if the curve is traced in the counterclockwise direction, at each vertex with code 1 the curve makes a left turn, and at each vertex with code 3 the curve makes a right turn. Such vertices are called salient and reentrant, [12, 13], respectively. In the hexagonal and the triangular grids, salient and reentrant vertices were also defined as those vertices at which the curve makes a left and a right turn, respectively [9]. It was shown [12, 13] that every simple closed curve in the square grid has four salient vertices more than it has reentrant ones. This result was generalized to arbitrary curves (not necessarily simple) in the square grid, and to curves in the hexagonal grid [8, 9]. In the latter grid, each curve has six more salient vertices than reentrant ones. This relationship between the number of salient and reentrant vertices was used in the study of the tiling problem on the square and hexagonal grids [10]. It was also shown [9] that there is no similar relationship between the number of salient and reentrant vertices in the triangular grid.

Here, we propose a finer classification of the vertices on a simple closed curve in the triangular grid, based on the number of incident interior triangles, i.e., based on the angle the curve makes at the vertex. We call such vertices (type 1 and type 2) convex and concave vertices. We prove a relationship between the number of different types of convex and concave vertices that every simple closed curve in the triangular grid satisfies.

2 Preliminaries

We introduce some basic notions on the regular grids in 2D [15, 26], on simple closed curves [4, 19] and on salient and reentrant vertices in these grids [9, 13].

2.1 Regular Grids in the Plane

There are three regular grids in the plane: the triangular, square and hexagonal grids. They induce the tessellations of the plane into regular triangles, squares and hexagons, respectively, called pixels. Each triangle, square and hexagon is incident to three, four and six edges and vertices, respectively. Each edge (in all three grids) is incident to two vertices and two pixels. Two vertices incident to the same edge are called neighbors. Each vertex in the triangular, square and hexagonal grids is incident to six, four and three pixels and edges, and has six, four and three neighbors, respectively.

Different types of adjacency relations are defined between the pixels in these grids, depending on their intersection. Edge-adjacent pixels share an entire edge; (strictly) vertex-adjacent pixels share (only) a vertex. Each triangle is edge-adjacent to three triangles, one across each of its edges. It is strictly vertex-adjacent to another nine triangles, three across each of its vertices. Each square is edge-adjacent to four squares, and is strictly vertex-adjacent to other four squares. Each hexagon is edge-adjacent to six hexagons. Two hexagons that share a vertex, share also an entire edge. Thus, there is no strict vertex-adjacency in the hexagonal grid.

A (binary) object O in these grids is a finite set of pixels in the grid. The pixels in O are called black (object), those in the complement $O^c$ of O are called white (background). Two pixels p and q in an object O are edge-connected (vertex-connected) in O, if there is a sequence of pixels in O, starting at p and ending in q, such that any two consecutive pixels in the sequence are edge-adjacent (vertex-adjacent).

2.2 Simple Closed Curves in the Regular Grids

A simple closed curve C of length k in a grid is a cyclic sequence $v_1,e_1,v_2,e_2,...,v_k, e_k,v_{1}$, of grid vertices $v_i$ and grid edges $e_i$, $1\le i\le k$, if each vertex in the sequence C is shared by the previous and the next edge in C and there is no repetition of vertices (or of edges) in C. Thus, C is a discrete 1-surface [18] and it defines a (polygonal) Jordan curve. Two consecutive vertices in the sequence are called adjacent on C. We will assume that C is oriented counterclockwise.

The interior of the simple closed curve C is composed of a finite set S of grid pixels, called interior pixels of C. Such sets S in the square [27] and in the triangular grid [11] are called well-composed or gapless [6, 7]. In the hexagonal grid, each such set of pixels (hexagons) is well-composed, due to the restricted number of pixels incident to a vertex in the hexagonal grid (three, as opposed to four in the square and six in the triangular grid). The pixels in the complement $S^c$ of S are called exterior pixels. The set of pixels incident to a vertex v on a simple closed curve C can be divided in two edge-connected subsets: the edge-connected subset of interior pixels, and the edge-connected subset of exterior pixels of C.

2.3 Salient and Reentrant Vertices in the Regular Grids

For the counterclockwise orientation of a simple closed curve C, the set S of interior pixels is on the left side of C. At each vertex v on C, the curve C makes a left turn, a right turn, or continues straight ahead. Salient and reentrant vertices in the three regular grids are defined as vertices at which the curve C makes a left and right turn, respectively.

In the square grid, if the curve C makes a left turn at v, the salient vertex v is incident to exactly one interior square (and exactly three exterior squares). If C makes a right turn at v, the reentrant vertex v is incident to exactly three interior squares (and one exterior square). If C continues straight at v, then v is incident to exactly two edge-adjacent interior squares (and two edge-adjacent exterior ones). As C is simple, the vertex v cannot be incident to exactly two strictly vertex-adjacent interior squares (and two strictly vertex-adjacent exterior ones).

It was shown [9, 13, 35] that for a simple closed curve C in the square grid, the number $n^+$ of salient vertices is larger by 4 than the number $n^-$ of reentrant vertices, i.e.,

$$n^+-n^-=4.$$

In the hexagonal grid, a salient vertex v on a curve C is incident to exactly one interior hexagon, and exactly two exterior ones. A reentrant vertex is incident to exactly two interior hexagons, and exactly one exterior hexagon. The number $n^+$ of salient vertices is larger by 6 than the number $n^-$ of reentrant vertices [9], i.e.,

$$n^+-n^-=6.$$

In the triangular grid, a salient vertex is incident to one or two interior triangles and to five or four edge-connected exterior triangles, respectively. A reentrant vertex is incident to five or four edge-connected interior triangles and to one or two exterior triangles, respectively. There is no (nontrivial) combinatorial relationship between the number of salient and reentrant vertices on C of the form

$$kn^++ln^-=m$$

for some integers k, l and m. For example [9], the boundary curve of a single triangle has three salient and no reentrant vertices, while the boundary curve of two edge-adjacent triangles has four salient and no reentrant vertices.

3 Convex and Concave Vertices in the Triangular Grid

We obtain a combinatorial relationship between different types of vertices on a simple closed curve C in the triangular grid by making a distinction between different types of salient and reentrant vertices, based on the number of incident interior and exterior triangles, i.e., based on the angle at which the curve C turns at the vertex.

At a vertex v on a simple closed curve C in the triangular grid, the curve C can make a turn left at the angle $\pi /3$ or $2\pi /3$, a turn right at the same angles, or it can continue straight ahead.

Definition 1

A vertex v on a counterclockwise oriented simple closed curve C in the triangular grid is called convex (concave) if C turns left (right) at v. If the turning angle is $\pi /3$, the vertex is of type 1; if the angle is $2\pi /3$ it is of type 2. If C makes no turn at v, then v is called straight.

The different types (up to rotation) of vertices are illustrated in Fig. 1.

Fig. 1.

The possible configurations (up to rotation) of interior (dark) and exterior (white) triangles around a vertex on a curve in the triangular grid: (a) type 1 convex; (b) type 2 convex; (c) straight; (d) type 1 concave; (e) type 2 concave.

Each type 1 convex vertex is incident to one interior triangle (and five exterior ones), and each type 2 convex vertex is incident to two edge-adjacent interior triangles (and four edge-connected exterior ones). Each type 1 concave vertex is incident to one exterior triangle (and five interior ones), and each type 2 concave vertex is incident to two edge-adjacent exterior triangles (and four edge-connected interior ones).

We denote as $n^+_1$, $n^+_2$, $n^-_1$ and $n^-_2$ the number of type 1 convex, type 2 convex, type 1 concave and type 2 concave vertices on a simple closed curve C, respectively. We will show that

$$2n^+_1+n^+_2-2n^-_1-n^-_2=6,$$

i.e.,

$$A(C)=n^+_1+n^+_2/2-n^-_1-n^-_2/2=3.$$

The explanation follows from considering some simple cases.

• If C is the boundary curve of a single triangle, it has three type 1 convex vertices ($n^+_1=3$), and $A(C)=3$.

• If C is the boundary curve of two edge-adjacent triangles, it has two type 1 convex vertices and two type 2 convex ones ($n^+_1=n^+_2=2$), and $A(C)=2+2/2=3$.

• If C is the boundary curve of five triangles incident to a vertex v, it has two type 1 convex, four type 2 convex and one type 1 concave vertex ($n^+_1=2$, $n^+_2=4$, $n^-_1=1$), and $A(C)=2+4/2-1=3$.

• If C is the boundary curve of four edge-connected triangles incident to a vertex v, it has two type 1 convex, three type 2 convex and one type 2 concave vertex ($n^+_1=2$, $n^+_2=3$, $n^-_2=1$), and $A(C)=2 +3/2-1/2=3.$

In the following, we give a formal proof of this combinatorial relationship.

Proposition 1

For a simple closed curve C in the triangular grid,

$$A(C)=n^+_1+n^+_2/2-n^-_1-n^-_2/2=3.$$

Proof

The proof is by induction on the length n of C.

By the above discussion for convex vertices, the claim is true for the base cases $n=3,4.$

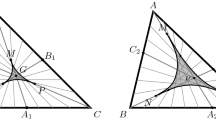
For the inductive step, let the proposition be true for all curves of length smaller than n and let C be a curve of length $n\ge 5$. Let us assume, without loss of generality, that the triangular grid is oriented so that it has $\bigtriangledown$ and $\bigtriangleup$ shaped triangles. In this orientation, each vertex has an east, west, south-east, south-west, north-east and north-west neighbor. Let v be the vertex on C with the smallest x Cartesian coordinate among those with the largest y coordinate (v is the leftmost of the topmost vertices on C). The vertex v is necessarily a convex vertex. We denote by $e_1$ and $e_2$ the previous and the next edge of the vertex v on C, and by $v_1$ and $v_2$ the other endpoints of the edges $e_1$ and $e_2$, respectively.

Fig. 2.

The different cases in the proof of Proposition 1. The topmost leftmost vertex v on the curve C is: (a) and (b) a type 1 convex vertex; (c) and (d) a type 2 concave vertex with the south-east neighbor $v'$ adjacent on C to the vertex $v_1$ or the vertex $v_2$, respectively; (e) and (f) a type 2 convex vertex with type 1 concave south-east neighbor $v'$ on C not adjacent on C to $v_1$ or $v_2$; (g) a type 2 convex vertex with type 2 concave south-east neighbor $v'$ on C not adjacent on C to $v_1$ or $v_2$; (h) a type 2 convex vertex with south-east neighbor $v'$ not on C.

We will distinguish several cases, depending on the type of the vertex v (v is type 1 convex (case 1) or type 2 convex (case 2)) and, in case 2, depending on the south-east neighbor $v'$ of the vertex v ($v'$ is adjacent on C to $v_1$ or $v_2$ (case 2a); $v'$ is not adjacent on C to either $v_1$ or $v_2$ and $v'$ is a type 1 concave vertex on C (case 2b); $v'$ is not adjacent on C to either $v_1$ or $v_2$ and $v'$ is a type 2 concave vertex on C (case 2c); $v'$ is not on C (case 2d)). The different configurations are illustrated in Fig. 2.

• 1. If v is a type 1 convex vertex, then the vertices $v_1$ and $v_2$ are neighbors, and they determine the edge $e=v_1v_2$ in the triangular grid. Since there are no repetitions of vertices or edges in C, the edge e does not belong to C. Replacement of the vertex v and edges $e_1$ and $e_2$ with the edge e produces a curve of length $n-1$, for which the proposition is true. This replacement

  • removes from C one type 1 convex vertex (the vertex v), decreasing the quantity A(C) by 1;

  • changes the type of the vertices $v_1$ and $v_2$ by changing the angle the curve makes at them, increasing the quantity A(C) by 1/2 for each of the two vertices $v_1$ and $v_2$.

  Neither of the two vertices $v_1$ and $v_2$ is a type 1 convex vertex, because the length n of C is greater than 4 and C is a simple closed curve. The possible cases for the vertex $v_1$ before and after the replacement are illustrated in Figs. 3 and 4, and for the vertex $v_2$ in Figs. 5 and 6. We give details for the vertex $v_1$, the analysis for the vertex $v_2$ being similar. The possible types for the vertex $v_1$ depend on the edge $e_1$ being horizontal or not.

  • If the edge $e_1$ connecting the vertices $v_1$ and v is a horizontal edge, then the vertex $v_1$ is not a concave vertex, because of the choice of the vertex v. In this case, the vertex $v_1$ can be a straight vertex, or a type 2 convex vertex (see Fig. 3 (top)). The replacement of the vertex v and the edges $e_1=v_1v$ and $e_2=vv_2$ with the edge $e=v_1v_2$ decreases by one the number of interior triangles incident to $v_1$ (see Fig. 3 (bottom)). It thus transforms

    • a type 2 convex vertex to a type 1 convex vertex, decreasing $n^+_2$ by 1 and increasing $n^+_1$ by 1;

    • a straight vertex to a type 2 convex vertex, increasing $n^+_2$ by 1;

  • If the edge $e_1$ joining the vertices $v_1$ and v is not horizontal, then the vertex $v_1$ can also be a type 1 or type 2 concave vertex. The replacement in these two cases transforms

    • a type 1 concave vertex to a type 2 concave vertex, decreasing $n^-_1$ by 1 and increasing $n^-_2$ by 1.

    • a type 2 concave vertex to a straight vertex, decreasing $n^-_2$ by 1;

  Each of these changes increases the quantity A(C) by 1/2. The possible configurations around the vertex $v_1$ before and after the replacement in the case when the edge $e_1$ is not horizontal are illustrated in Fig. 4.

  The type of the vertex $v_2$ also depends on the edge $e_1$ being horizontal or not. Similarly as for the vertex $v_1$, the change of the type of the vertex $v_2$ induced by the replacement increases the quantity A(C) by 1/2, as illustrated in Figs. 5 and 6.

  Thus, the total change in the quantity A(C) induced by this replacement is equal to $-1+1/2+1/2=0$, i.e., the proposition is true for the curve C.

• 2. If v is a type 2 convex vertex, then v is incident to two edge-adjacent interior triangles. Let $e'$ be the common edge of the two triangles. The other endpoint of $e'$ is the south-east neighbor $v'$ of v. We distinguish several cases depending on the vertex $v'$.

  • 2a. If the vertex $v'$ is adjacent on C to $v_1$, then $v_1$ is a type 1 convex vertex (see Fig. 2 (c)) and it can be replaced, together with its two incident edges $v'v_1$ and $v_1v$, with the edge $e'=v'v$. In the same way as for the type 1 convex vertex v above it can be shown that the replacement decreases the length of the curve by 1 and it does not change the quantity A(C). A similar argument holds if the vertex $v'$ is adjacent on C to the vertex $v_2$ (see Fig. 2 (d)). The vertex $v'$ cannot be adjacent on C to both $v_1$ and $v_2$ because the length of the (simple closed) curve C is greater than 4.

  • 2b. If the vertex $v'$ is not adjacent on C to either $v_1$ or $v_2$ and $v'$ is a type 1 concave vertex on the curve C (see Figs. 2 (e) and (f)), we denote $e_1'$ and $e_2'$ the previous and the next edge on C incident to $v'$, respectively. We can bypass $v'$ and its two incident edges $e'_1$ and $e'_2$, as we did with the type 1 convex vertex v above, replacing them with the edge connecting the other two endpoints of the edges $e'_1$ and $e'_2$. A similar analysis as above shows that the quantity A(C) remains unchanged, and the length of the curve decreases by 1.

  • 2c. If the vertex $v'$ is not adjacent on C to either $v_1$ or $v_2$ and $v'$ is a type 2 concave vertex on C (see Fig. 2 (g)), then the edges on C incident to v and those incident to $v'$ are pairwise parallel. We split the curve C into two curves $C_1$ and $C_2$. The curve $C_1$ is obtained by connecting the vertex v to the vertex $v'$, and taking the part of the curve C from the vertex $v'$ and the edge $e'_2$ to the edge $e_1$ and the vertex v. The curve $C_2$ is obtained in a similar fashion by connecting the vertex $v'$ to the vertex v, and taking the part of the curve C from the vertex v and the edge $e_2$ to the edge $e'_1$ and the vertex $v'$. Both curves $C_1$ and $C_2$ are simple closed counterclockwise oriented curves. They are both shorter than the curve C (at least by 2), and proposition is valid for the two curves. The sum $A(C_1)+A(C_2)$ of the quantities A of the two curves is 6. The split of the curve C into $C_1$ and $C_2$ induces the following changes:

    • The type 2 convex vertex v is replaced by two type 1 convex vertices, one on the curve $C_1$ and the other on $C_2$, increasing the total count of the quantity A(C) by $-1/2+1+1=3/2$.

    • The type 2 concave vertex $v'$ is replaced by two type 2 convex vertices, one on each of the curves $C_1$ and $C_2$, increasing the total count of the quantity A(C) by $-(-1/2)+1/2+1/2=3/2$.

    Thus, the total increase in the quantity $A(C_1)+A(C_2)$ obtained by the vertex count is $3/2+3/2=3$, which exactly accounts for the increased number of curves (two curves $C_1$ and $C_2$ instead of one curve C) after the split.

  • 2d. If the vertex $v'$ is not on the curve C, we replace the vertex v and its two incident edges $e_1$ and $e_2$ in C with the vertex $v'$ and the edges $v'v_1$ and $v'v_2$, respectively. The new curve is of the same length as C.

    • The type 2 convex vertex v is replaced with the type 2 concave vertex $v'$, decreasing the quantity A(C) by 1.

    • The vertices $v_1$ and $v_2$ loose one incident interior triangle each, increasing the quantity A(C) in total by 1.

    Thus, the total change in the quantity A(C) induced by this replacement is $-1+1=0$. The vertex $v_1$ has the same y coordinate as the vertex v, and it is the vertex with the smallest x coordinate among the vertices with that y coordinate. The vertex $v_1$ now takes the role of the vertex v: it is either a type 1 or a type 2 convex vertex. We process it in the same way as the vertex v. We either

    • decrease the length of the curve (if the vertex $v_1$ is a type 1 convex vertex; if $v_1$ is a type 2 convex vertex with the south-east neighbor adjacent on C to one of the neighbors of $v_1$ on C; if $v_1$ is a type 2 convex vertex with a type 1 concave south-east neighbor not adjacent on C to either of the two neighbors of $v_1$ on C),

    • split the curve in two (if $v_1$ is a type 2 convex vertex with the type 2 concave south-east neighbor), or

    • eliminate the vertex $v_1$, keeping the length of the curve, making its east neighbor the vertex with the smallest x coordinate among those vertices with the largest y coordinate.

    This process will continue until the curve is shortened or split in two shorter curves, or until the last vertex $v''$ on C with the same y coordinate as the vertices v and $v_1$ is reached. The vertex $v''$ is either a type 1 convex vertex, or it becomes a type 1 convex vertex after the final replacement of two edges in C with another two edges at the vertex following $v''$ on C. At this point, the vertex $v''$ is eliminated decreasing the length of C and maintaining the quantity A(C).

Fig. 3.

The possible configurations around the vertex $v_1$ if the vertex v is type 1 convex and the edge $e_1=v_1v$ is horizontal (top) before and (bottom) after the replacement. (a) A type 2 convex vertex $v_1$ becomes type 1 convex. (b) A straight vertex $v_1$ becomes type 2 convex.

Fig. 4.

The possible configurations around the vertex $v_1$ if the vertex v is type 1 convex and the edge $e_1=v_1v$ is not horizontal (top) before and (bottom) after the replacement. (a) A type 1 concave vertex $v_1$ becomes type 2 concave. (b) A type 2 concave vertex $v_1$ becomes straight. (c) A straight vertex $v_1$ becomes type 2 convex. (d) A type 2 convex vertex $v_1$ becomes type 1 convex.

Fig. 5.

The possible configurations around the vertex $v_2$ if the vertex v is type 1 convex and the edge $e_1=v_1v$ is horizontal (top) before and (bottom) after the replacement. (a) A type 2 convex vertex $v_2$ becomes type 1 convex. (b) A straight vertex $v_2$ becomes type 2 convex. (c) A type 2 concave vertex $v_2$ becomes straight. (d) A type 1 concave vertex $v_2$ becomes type 2 concave.

Fig. 6.

The possible configurations around the vertex $v_2$ if the vertex v is type 1 convex and the edge $e_1=v_1v$ is not horizontal (top) before and (bottom) after the replacement. (a) A type 2 convex vertex $v_2$ becomes type 1 convex. (b) A straight vertex $v_2$ becomes type 2 convex. (c) A type 2 concave vertex $v_2$ becomes straight.

4 Summary and Future Work

We gave a classification of convex and concave vertices on a simple closed curve in the triangular grid, based on the angle at which the curve turns at the vertex, i.e., based on the number of interior triangles incident to the vertex, thus refining the existing classification into salient and reentrant vertices. We showed a combinatorial relationship between the number of convex and concave vertices of different types.

We plan to extend this work to general (non-simple) closed curves and to curves in semiregular grids.