Abstract
We systematize and generalize recent results of Gerlach and Glück on the strong convergence and spectral theory of bounded (positive) operator semigroups (T s)s ∈ S on Banach spaces (lattices). (Here, S can be an arbitrary commutative semigroup, and no topological assumptions neither on S nor on its representation are required.) To this aim, we introduce the “semigroup at infinity” and give useful criteria ensuring that the well-known Jacobs–de Leeuw–Glicksberg splitting theory can be applied to it.
Next, we confine these abstract results to positive semigroups on Banach lattices with a quasi-interior point. In that situation, the said criteria are intimately linked to the so-called AM-compact operators (which entail kernel operators and compact operators); and they imply that the original semigroup asymptotically embeds into a compact group of positive invertible operators on an atomic Banach lattice. By means of a structure theorem for such group representations (reminiscent of the Peter–Weyl theorem and its consequences for Banach space representations of compact groups) we are able to establish quite general conditions implying the strong convergence of the original semigroup.
Finally, we show how some classical results of Greiner (Sitzungsberichte der Heidelberger Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse, 55–80, 1982), Davies (J Evol Equ 5(3), 407–415, 2005), Keicher (Arch Math (Basel) 87(4), 359–367, 2006) and Arendt (Positivity 12(1), 25–44, 2008) and more recent ones by Gerlach and Glück (Convergence of positive operator semigroups, 2017) are covered and extended through our approach.
Dedicated to Ben de Pagter on the occasion of his 65th birthday
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
We apologize for this little abuse of terminology.
References
Y. Abramovich, G. Sirotkin, On order convergence of nets. Positivity 9(3), 287–292 (2005)
W. Arendt, Positive semigroups of kernel operators. Positivity 12(1), 25–44 (2008)
W. Arendt, A.V. Bukhvalov, Integral representations of resolvents and semigroups. Forum Math. 6(1), 111–135 (1994)
D. Axmann, Struktur-und Ergodentheorie irreduzibler Operatoren auf Banachverbänden. PhD thesis, Eberhard-Karls-Universität zu Tübingen, 1980
A.V. Bukhvalov, Integral representation of linear operators. J. Math. Sci. 9(2), 129–137 (1978)
E.B. Davies, Triviality of the peripheral point spectrum. J. Evol. Equ. 5(3), 407–415 (2005)
M. de Jeu, M. Wortel, Compact groups of positive operators on Banach lattices. Indag. Math. (N.S.) 25(2), 186–205 (2014)
T. Eisner, B. Farkas, M. Haase, R. Nagel, Operator Theoretic Aspects of Ergodic Theory. Graduate Texts in Mathematics, vol. 272 (Springer, Cham, 2015)
E.Yu. Emel’yanov, U. Kohler, F. Räbiger, M.P.H. Wolff, Stability and almost periodicity of asymptotically dominated semigroups of positive operators. Proc. Am. Math. Soc. 129(9), 2633–2642 (2001)
K.-J. Engel, R. Nagel, One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194 (Springer, New York, 2000). With contributions by S. Brendle, M. Campiti, T. Hahn, G. Metafune, G. Nickel, D. Pallara, C. Perazzoli, A. Rhandi, S. Romanelli and R. Schnaubelt
M. Gerlach, On the peripheral point spectrum and the asymptotic behavior of irreducible semigroups of Harris operators. Positivity 17(3), 875–898 (2013)
M. Gerlach, Semigroups of Kernel operators. PhD thesis, Universität Ulm, 2014. https://doi.org/10.18725/OPARU-3263
M. Gerlach, J. Glück, On a convergence theorem for semigroups of positive integral operators. C. R. Math. Acad. Sci. Paris 355(9), 973–976 (2017)
M. Gerlach, J. Glück, Convergence of positive operator semigroups (2017). Preprint: arxiv.org/abs/1705.01587v1
G. Greiner, Spektrum und Asymptotik stark stetiger Halbgruppen positiver Operatoren. Sitzungsberichte der Heidelberger Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse (Springer, Berlin, 1982), pp. 55–80
G. Greiner, R. Nagel, La loi “zéro ou deux” et ses conséquences pour le comportement asymptotique des opérateurs positifs. J. Math. Pures Appl. (9) 61(3), 261–273 (1982)
J.J. Grobler, P. van Eldik, A characterization of the band of kernel operators. Quaest. Math. 4(2), 89–107 (1980/1981)
V. Keicher, On the peripheral spectrum of bounded positive semigroups on atomic Banach lattices. Arch. Math. (Basel) 87(4), 359–367 (2006)
M.C. Kunze, Diffusion with nonlocal Dirichlet boundary conditions on unbounded domains (2018). Preprint: arxiv.org/abs/1810.04474v1
W.A.J. Luxemburg, A.C. Zaanen, Riesz Spaces. Volume I. North-Holland Mathematical Library (North-Holland/American Elsevier, Amsterdam/New York, 1971)
P. Meyer-Nieberg, Banach Lattices. Universitext (Springer, Berlin, 1991)
K. Pichór, R. Rudnicki, Continuous Markov semigroups and stability of transport equations. J. Math. Anal. Appl. 249(2), 668–685 (2000)
K. Pichór, R. Rudnicki, Asymptotic decomposition of substochastic operators and semigroups. J. Math. Anal. Appl. 436(1), 305–321 (2016)
K. Pichór, R. Rudnicki, Asymptotic decomposition of substochastic semigroups and applications. Stoch. Dyn. 18(1), 1850001 (2018)
H.H. Schaefer, Banach Lattices and Positive Operators. Die Grundlehren der mathematischen Wissenschaften, Band 215 (Springer, New York, 1974)
E. Scheffold, Das Spektrum von Verbandsoperatoren in Banachverbänden. Math. Z. 123, 177–190 (1971)
W. Wnuk, Banach Lattices with Order Continuous Norms (Polish Scientific Publishers PWN, Warsaw, 1999)
M.P.H. Wolff, Triviality of the peripheral point spectrum of positive semigroups on atomic Banach lattices. Positivity 12(1), 185–192 (2008)
A.C. Zaanen, Riesz Spaces II. North-Holland Mathematical Library, vol. 30 (North-Holland, Amsterdam, 1983)
Acknowledgements
Thank you, Ben, for having been a truly optimal boss at the Delft Institute of Applied Mathematics during my time there. You are a wonderful person, and the appreciation you showed for me and my work always made me very proud. Markus
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: AM-Compact Operators
Let E be a Banach lattice and F a Banach space. A bounded operator T : E → F is called AM-compact if T maps order intervals of E to relatively compact subsets of F.
The following is a useful characterization of AM-compactness in the case that E has a quasi-interior point y ∈ E +. Recall that this means that the principal ideal
is dense in E. We endow E y with its natural AM-norm
It is well known that this turns E y into a Banach lattice, isometrically lattice isomorphic to C(K) (with y being mapped to 1) for some compact Hausdorff space K (Krein–Krein–Kakutani theorem).
Lemma A.1
Let E be a Banach lattice with a quasi-interior point y ∈ E + , let F be any other Banach space and T : E → F a bounded operator. Then T : E y → F is compact if and only if T[0, y] is relatively compact, if and only if T is AM-compact.
Proof
Suppose that T : E y → F is compact. Then, T[0, y] is relatively compact. If the latter is the case, then for each c > 0 the set
is also relatively compact. Let u ∈ E + and ε > 0. Since y is a quasi-interior point, there is c > 0 such that u ∈ [−cy, cy] + B[0, ε]. We claim that
as well. Indeed, write u = z + r with \(\left \vert z\right \vert \le cy\) and ∥r∥≤ ε and let 0 ≤ x ≤ u. Then \(0 \le x \le \left \vert z\right \vert + \left \vert r\right \vert \le cy + \left \vert r\right \vert \). By the decomposition property, there are \(0 \le x_1 \le \left \vert z\right \vert \) and \(0 \le x_2\le \left \vert r\right \vert \) with x = x 1 + x 2. Hence x ∈ [−cy, cy] + B[0, ε] as claimed.
It follows from (A.1) that
Since T[−cy, cy] is relatively compact, it admits a finite ∥T∥ε-mesh. Hence, T[0, u] admits a finite 2∥T∥ε-mesh. As ε > 0 was arbitrary, T[0, u] is relatively compact.
Finally, if [u, v] is any non-empty order interval of E, then v − u ≥ 0 and T[u, v] = Tu + T[0, v − u] is relatively compact, by what we have already shown. □
The following theorem shows that AM-compactness is preserved when one passes to a factor lattice with respect to an invariant closed ideal.
Theorem A.2
Let E be a Banach lattice, let \(T\in \operatorname {\mathrm {\mathcal {L}}}(E)\) be AM-compact, and let I ⊆ E be a T-invariant closed lattice ideal in E. Then the induced operator
is also AM-compact.
Proof
Let 0 ≤ X ∈ E∕I. We have to show: the order interval [0, X] in E∕I is mapped by T ∕ to a relatively compact subset of E∕I.
Recall from [25, Prop. II.2.6] that for x, y ∈ E one has
In particular, there is x ≥ 0 such that X = x+I. Now, let 0 ≤ Y ≤ X be given. Then there are y ∈ E and z ∈ I such that y ≤ x + z and Y = y+I. Replacing z by \(\left \vert z\right \vert \) we may suppose in addition that z ≥ 0.
By the decomposition property, y + = a + b for some elements 0 ≤ a ≤ x and 0 ≤ b ≤ z. Then b ∈ I since I is an ideal and z ∈ I. As the canonical surjection is a lattice homomorphism, Y + = a+I and hence T ∕(Y +) = Ta+I. Similarly, one can show that there is c ∈ [0, x] with Y − = c+I. It follows that
and hence T ∕([0, X]) ⊆ T([−x, x]) + I. Since T is AM-compact, the set T([−x, x]) is relatively compact in E, and hence so is T([−x, x]) + I in E∕I. This implies that T ∕([0, X]) is relatively compact, as desired. □
1.1 Examples of AM-Compact Operators
In the remainder of this appendix we consider two results that help to identify AM-compact operators. The first tells that every integral operator is AM-compact. This is a well-known consequence of abstract theory (see, e.g., the discussion at the beginning of [14, Section 4], which is based on abstract results in [21, Corollary 3.7.3] and [25, Proposition IV.9.8]). Gerlach and Glück give an elementary proof involving measure-theoretic (i.e., almost everywhere) arguments [14, Proposition A.1]. Our proof is a little less elementary, but replaces the measure theory by functional analysis.
Theorem A.3
Let X and Y be measure spaces and let 1 ≤ p, q < ∞. Let, furthermore, \(k: X \times Y \to \mathbb {R}_+\) be a measurable mapping such that by
a bounded operator

is (well) defined. Then T is AM-compact.
Proof
Let the measure spaces be X = (X, Σ
X, μ
X) and Y = (Y, Σ
Y, μ
Y). Let  . We have to show that
. We have to show that  is relatively compact.
is relatively compact.
Suppose first that both measures μ
X and μ
Y are finite, u = 1 and  . Then, in particular,
. Then, in particular,  . Since
. Since  is dense in
is dense in  ,
,  is compact. But T factors through
is compact. But T factors through  (since T
1 is bounded) and since on closed
(since T
1 is bounded) and since on closed  -balls the
-balls the  - and the
- and the  -topology coincide,
-topology coincide,  is compact. In particular, T[0, 1] is relatively compact in
is compact. In particular, T[0, 1] is relatively compact in  .
.
In the general case, consider the operator

Because of [0, u] = u ⋅ [0, 1] it suffices to show that  is relatively compact. Hence, one may suppose without loss of generality that μ
Y is finite and u = 1.
is relatively compact. Hence, one may suppose without loss of generality that μ
Y is finite and u = 1.
Under this assumption let

and, for \(n \in \mathbb {N}\),

Define T n by
Observe that  and it is supported on a set of finite measure. So, by what we have shown first,
and it is supported on a set of finite measure. So, by what we have shown first,  is compact. Now,
is compact. Now,

and hence

Consequently, also  is compact, and this concludes the proof. □
is compact, and this concludes the proof. □
We turn to a second class of examples of AM-compact operators.
Theorem A.4
Let X and Y be measure spaces, let 1 ≤ p, q < ∞, and let

be a positive operator with the following property: There is a sequence (A n)n in Σ X such that ⋃n A n = X and such that

Then T is AM-compact.
Proof
By performing the same reduction as in the proof of Theorem A.3 above, we may suppose without loss of generality that Y is a finite measure space. It remains to show that T[0, 1] is relatively  -compact.
-compact.
Define the projection P
n on  by
by
By hypothesis and the dominated convergence theorem, P
n
T → T uniformly on order intervals of  , hence in particular with respect to the norm of
, hence in particular with respect to the norm of  . Therefore, it suffices to consider the case that also X is a finite measure space, and
. Therefore, it suffices to consider the case that also X is a finite measure space, and  . By the subsequent Lemma A.5 we are done. □
. By the subsequent Lemma A.5 we are done. □
Lemma A.5
Let X and Y be finite measure spaces, 1 ≤ p, q < ∞ and  a bounded operator with
a bounded operator with  . Then for each 1 < r ≤∞ with r ≥ p the operator
. Then for each 1 < r ≤∞ with r ≥ p the operator

is compact.
Proof
We may suppose 1 < p = r < ∞. By the closed graph theorem,  is bounded. If (f
n)n is a bounded sequence in
is bounded. If (f
n)n is a bounded sequence in  , it has a weakly convergent subsequence (by reflexivity). Hence, (Tf
n)n has a weakly convergent subsequence in
, it has a weakly convergent subsequence (by reflexivity). Hence, (Tf
n)n has a weakly convergent subsequence in  . But a weakly convergent sequence in
. But a weakly convergent sequence in  converges strongly in
converges strongly in  since X is a finite measure space. (Represent
since X is a finite measure space. (Represent  for some compact Hausdorff space K, and observe that in C(K) a sequence(!) is weakly convergent if and only if it is uniformly bounded and pointwise convergent.) □
for some compact Hausdorff space K, and observe that in C(K) a sequence(!) is weakly convergent if and only if it is uniformly bounded and pointwise convergent.) □
Remarks A.6
-
1)
Actually, one can reduce Theorem A.4 to Theorem A.3 by employing Bukhvalov’s characterization of integral operators [5], variants of which are, for instance, discussed in [17, Theorem 3.9], [29, Theorem 96.5], [3, Theorem 1.5] and [12, Theorem 4.2.12]
-
2)
For 1 ≤ p ≤ 2, Lemma A.5 has a much more elementary proof. Indeed, by quite elementary arguments one can show that T is a Hilbert–Schmidt operator when considered as an operator
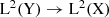 .
. -
3)
In the proof of Lemma A.5 we have used that, for a finite measure space X, a sequence which converges weakly in
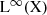 must converge strongly on
must converge strongly on 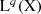 for each 1 ≤ q < ∞. It would be nice to have a more elementary proof of this fact, avoiding the representation
for each 1 ≤ q < ∞. It would be nice to have a more elementary proof of this fact, avoiding the representation 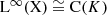 .
.
Appendix B: Universal Nets
In this appendix we treat, for the convenience of the reader, a useful but maybe not so widely known concept from general topology.
Let (I, ≤) be any directed set. A subset A of I is called a tail of I if it is of the form A = {α ∈ I | α ≥ α 0} for some α 0 ∈ I. And it is called cofinal if its complement does not contain a tail. Equivalently, A is cofinal if for each α 0 ∈ I there is α ≥ α 0 such that α ∈ A. Clearly, each tail is cofinal.
A tail of a net (x α)α ∈ I in a set X is a subset of the form {x α | α ∈ A}, where A ⊆ I is a tail of I. A net (x α)α is called universal or an ultranet, if for each Y ⊆ X either the set Y or its complement contains a tail of the net. If f : X 1 → X 2 is a mapping and (x α)α is a universal net in X 1, then (f(x α))α is a universal net in X 2. Likewise, a subnet of a universal net is universal.
Lemma B.1
Each net has a universal subnet.
Proof
Let (x α)α be a net in a set X. Then the tails of the net form a filter base, hence by Zorn’s lemma there is an ultrafilter \(\mathcal {U}\) containing all the tails. For β ∈ I and \(U \in \mathcal {U}\) there is α(β, U) ∈ I such that α(β, U) ≥ β and x α(β,U) ∈ U. The set \(I \times \mathcal {U}\) is directed by
The net (x α(β,U))β,U is a universal subnet of (x α)α. □
Since a universal net in a topological space X converges if and only if it has a convergent subnet, X is compact if and only if each universal net in X converges.
Lemma B.2
Let X be a metric space and let (x α)α ∈ I be a net in X. Consider the following three assertions:
-
(i)
For each ε > 0 there is a compact set K ⊆ X such that B[K, ε] contains a tail of (x α)α.
-
(ii)
For each ε > 0 there is z ∈ X such that {α | x α ∈B[z, ε]} is cofinal.
-
(iii)
The net (x α)α is a Cauchy net.
Then (iii) ⇒ (i) ⇒ (ii) . And if (x α)α ∈ I is universal, also (ii) ⇒ (iii) . (Hence, in the latter case, all three assertions are equivalent.)
Proof
(iii) ⇒ (i): Let ε > 0. Then there is α ∈ I such that d(x β, x γ) ≤ ε for all β, γ ≥ α. Hence B[{x α}, ε] contains the tail {x β | β ≥ α}.
(i) ⇒ (ii): Let ε > ε′ > 0. Then there is a finite subset F ⊆ K such that K ⊆⋃z ∈ FB(z, ε′). Hence, by (ii), the set ⋃z ∈ FB[z, 2ε] contains a tail of (x α)α. Since F is finite, there is z ∈ F such that {α | x α ∈B[z, 2ε]} is cofinal.
(ii) ⇒ (iii): Suppose that (x α)α is universal, let ε > 0 and pick z as in (ii). By the universality of the net either the set A ε := {α | x α ∈B[z, ε]} or its complement contains a tail of I. But since A ε is cofinal, the second alternative is impossible. Hence, d(x α, x β) ≤ 2ε for all α, β from a tail of I. □
Theorem B.3
Let (x α)α ∈ I be a net in a regular topological space X and let
be its set of cluster points. Consider the following assertions:
-
(i)
Each subnet of (x α)α ∈ I has a cluster point.
-
(ii)
Each universal subnet of (x α)α ∈ I converges.
-
(iii)
For each cofinal subsequence \((\alpha _n)_{n \in \mathbb {N}}\) the sequence \((x_{\alpha _n})_{n \in \mathbb {N}}\) has a cluster point.
-
(iv)
The set C is non-empty and compact.
Then (i) ⇔ (ii) ⇒ (iii) and (i) ⇒ (iv) . If, in addition, I admits a cofinal sequence and X is metrizable, then (iii) ⇒ (iv) as well.
Proof
(i) ⇔ (ii): This follows from Lemma B.1 and the fact that a universal net converges if and only if it has a cluster point.
(i) ⇒ (iv): By hypothesis, the net (x α)α ∈ I itself has a cluster point, so C ≠ ∅. Let (y j)j ∈ J be a universal net in C. It suffices to show that (y j)j converges. Let
be directed by
For each (α, j, U) ∈ M one has y j ∈ U and hence there is
Then the mapping φ : M → I is cofinal, so (x φ(α,j,U))(α,j,U) ∈ M is a subnet. By hypothesis (i), this subnet has a cluster point y ∈ X, say. We prove that y j → y.
To this end, let V be any open neighborhood of y in X. Since X is regular, there is an open set W such that \(y\in W \subseteq \overline {W} \subseteq V\). It suffices to show that \(\overline {W}\) contains a tail of (y j)j. Suppose that this is not the case. Then, since that net is universal, the complement \(U_0 := X \setminus \overline {W}\) contains tail of (y j)j. This means that there is j 0 ∈ J such that y j ∈ U 0 for all j ≥ j 0. In particular, (α, j 0, U 0) ∈ M for all α ∈ I.
Fix α 0 ∈ I. Then, since y is a cluster point of (x φ(m))m ∈ M and W is an open neighborhood of y, there is M ∋ (α, j, U) ≥ (α 0, j 0, U 0) with x φ(α,j,U) ∈ W. But by the construction of φ we have also x φ(α,j,U) ∈ U ⊆ U 0. Since U 0 ∩ W = ∅, this yields a contradiction and the proof is complete.
(i) ⇒ (iii): This is trivial, as the sequence \((x_{\alpha _n})_n\) is a subnet of (x α)α whenever (α n)n is a cofinal sequence in I.
(iii) ⇒ (iv): Suppose that d is a metric inducing the topology of X and that I admits cofinal sequences. It then follows from (iii) that C ≠ ∅. In order to see that C is compact, let (y n)n be a sequence in C and let (α n)n be a cofinal sequence in I. Recursively, one can find a sequence \((x_{\beta _n})_n\) such that β n ≥ α n and \(d(x_{\beta _n}, y_n) \le \frac {1}{n}\). By (iii), \((x_{\beta _n})_n\) has a cluster point. Since X is metric, this means that \((x_{\beta _n})_n\) has a convergent subsequence. But then (y n)n also has convergent subsequence, and as C is closed, the limit of this subsequence lies in C. □
Appendix C: Some Notions from Semigroup Theory
A semigroup is a non-empty set S together with an associative operation S × S → S, generically called “multiplication.” A subset M of a semigroup S is multiplicative, if M ⋅ M ⊆ M. A non-empty multiplicative subset is a subsemigroup. A non-empty subset J of a semigroup S is a (two-sided) ideal of S if SJ ∪ JS ⊆ J. Each ideal is a subsemigroup.
A neutral element in a semigroup is any element e ∈ S such that es = se = s for all s ∈ S. There is at most one neutral element; if there is none, one can adjoin one in a standard way.
A semigroup S is called Abelian or commutative if st = ts for all s, t ∈ S. It is common to write Abelian semigroups additively, and denote their neutral elements by 0.
An Abelian semigroup S is called cancellative if it satisfies the implication
for all s, t, t′∈ S. By a standard result from semigroup theory, S is faithfully embeddable into a group if and only if S is cancellative. In this case, one usually considers S as a subset of some group G such that G = S−S. The (necessarily Abelian) group G is then unique up to canonical isomorphism and is called the group generated by S. In each case, when we speak of a group generated by an Abelian semigroup S, we have this meaning in mind, and in particular suppose tacitly that S is cancellative.
An Abelian semigroup S with neutral element 0 is called divisible, if for each s ∈ S and \(n \in \mathbb {N}\) there is t ∈ S such that nt = s. (This definition extends the common notion of divisibility from groups to semigroups.) And S is called essentially divisible if for each s ∈ S and \(n \in \mathbb {N}\) there are t 1, t 2 ∈ S such that nt 1 = s + nt 2.
Each divisible semigroup and each semigroup that generates a divisible group is essentially divisible.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Glück, J., Haase, M. (2019). Asymptotics of Operator Semigroups via the Semigroup at Infinity. In: Buskes, G., et al. Positivity and Noncommutative Analysis. Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-10850-2_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-10850-2_9
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-10849-6
Online ISBN: 978-3-030-10850-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



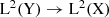 .
.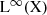 must converge strongly on
must converge strongly on 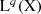 for each 1 ≤ q < ∞. It would be nice to have a more elementary proof of this fact, avoiding the representation
for each 1 ≤ q < ∞. It would be nice to have a more elementary proof of this fact, avoiding the representation 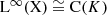 .
.