Point Cloud Noise and Outlier Removal with Locally Adaptive Scale

Abstract

This paper introduced a simple and effective algorithm to remove the noise and outliers in point sets generated by multi-view stereo methods. Our main idea is to discard the points that are geometrically or photometrically inconsistent with its neighbors in 3D space using the input images and corresponding depth maps. We attach a scale value to each point reflecting the influence to the adjacent area of the point and define a geometric consistency function and a photometric consistency function for the point. We employ a very efficient method to find the neighbors of a point using projection. The consistency functions are related to the normal and scale of the neighbors of points. Our algorithm is locally adaptive, feature preserving and easy to implement for massive parallelism. It performs robustly with a variety of noise and outliers in our experiments.

1 Introduction

The state of the art in multi-view stereo methods has seen great development in robustness and accuracy these years. However, point sets produced by multi-view stereo methods are usually redundant and inevitably with a lot of noise and outliers due to imperfection of acquisition hardware and algorithms, as is shown in Fig. 1(b). Modern MVS algorithms use different output scene representations, such as depth maps, a point cloud, or a mesh. Depth map scene representation is one of the most popular choices due to the flexibility and scalability [7] but suffers more noise. This poses a great challenge to surface reconstruction.

Fig. 1.

We use the multi-view stereo methods MVE [8] to reconstruct a dense 3D point cloud (b) for the Middlebury Temple dataset [11] (a). The output point cloud is very noisy. We denoise the depth maps only use geometric consistency (c). A lot of noise and outliers are removed but there are still some black points from the background retained on the border of the temple. We use geometric consistency and photometric consistency together in (d) and get better result.

We can impose strong regularization in MVS methods to reduce outliers, but this will destroy sharp features and may be time consuming. Some denoising methods directly operate on unorganized point cloud and using k nearest neighbors to optimize the position and normal of a reference point [13]. Depth map, however, often provides us with additional information such as connectivity and scale [3]. Therefore, in our method, we computed a scale value for each point using the input depth maps in image space. The scale value provides valuable information about the surface area each point was acquired from, as discussed by Fuhrmann et al. [3]. With scale information, we can handle datasets containing non-uniform noise and sample resolution.

In our method, we do not discretize the 3D space, avoiding large memory and time usage. We project a reference point to other depth maps and find its neighbors in the image space. The neighbors obtained from image space are not necessarily but most likely to be neighbors in the 3D space. Then we project them back to the 3D space to evaluate the geometric and photometric consistency between the reference point and its neighbors. Our locally adaptive geometric consistency function and photometric consistency are related to the scale of the reference point and it’s neighbors. The functions are defined compactly supported, namely, the neighbors used for evaluating the functions must be near the reference point in spatial space. Because of the redundancy of the depth maps, we do not change the position, normal and color of the points but just remove the points that are not consistent with its neighbors. For the sake of efficiency, we employ view selection strategy to identify nearby views using the feature points reconstructed in the previous SFM phase [6, 8]. This enables our methods the ability to operate on extremely large photo collections.

Our contributions are:

• An approach using scale information to evaluate the geometric and photometric consistency, which is local adaptive feature preserving and more accurate.

• Finding neighbors of reference points in image space by depth map triangulation and projection, which is very efficiency.

Fig. 2.

(1) A point with a scale value represents a finite surface in the spatial space. (2) The shape of the functions $f_{x}(x)$ (2a), $f_{y}(y)$ and $f_{z}(z)$ (2b), $w_{x}(x)$ (2c) and $w_{yz}(r)$ (2d).

In the remainder of this paper, we first review related work (Sect. 2). Then introduce our denoise approach (Sect. 3), perform experiments on a variety of data sets (Sect. 4) and conclude our work (Sect. 5).

2 Related Work

Here we describe some closely related work in point set denoising, focusing on how they handle point sets generated by images with varying resolution and viewing parameters, what parameters they use and to what extend they are time and memory consuming.

Most multi-view stereo methods integrate a depth map fusion strategy into the depth estimation stage or after the whole reconstruction. They usually enforce visibility and consistency across views. Wu et al. [18] firstly use an indicator function based on visibility cues in [16] to remove outliers. Then they enforce visibility consistency across views. Such method is not sophisticated thus there remains a lot of noise and outliers. Schönberger et al. [10] define a directed graph of consistent pixels with their photometric and geometric consistency support set, then find and fuse the clusters of consistent pixels in this graph. The fused point cloud are of high quality and have little outliers. However, finding clusters is very time consuming and not easy to parallelize. In addition, they use the photometric and geometric consistency terms computed in the MVS procedure of their reconstruction method, which are only available in their approach.

The above methods proposed as part of multi-view stereo methods usually use parameters that are unique in their depth reconstruction and thus their use is restricted. There are also some methods independent of the MVS. Sun et al. [13] directly denoise point clouds using the $L_{0}$ norm to preserving sharp features. Wolff et al. [17] take depth maps as input and implicitly uses a surface represented by the input depth maps to check geometric consistency and photometric consistency between each per-view point and other input views. Our method are relevant to their method, projecting the points to the image space of other depth maps. However, we take a completely different, local adaptive strategy to examine consistency using the finite surface represented by points with scale value.

The quality of the reconstructed surface strongly depends on the quality of the input point set which is inevitably with noise and outliers. Therefore, many surface reconstruction methods explicitly use some strategy to handle the noise and outliers. Poisson surface reconstruction [9] estimate local sampling density and scale the contribution of each point accordingly. However, sampling density is not necessarily related to the sample resolution, and an increased sampling density may simply be caused by data redundancy as discussed in [4]. Fuhrmann et al. [3] construct a discrete, multi-scale signed distance field capable of representing surfaces at multiple levels of detail and produce output surfaces that are adaptive to the scale of the input data. Our methods apply the same depth map triangulation step and compute the scale of every points. Fuhrmann et al. [4] attach the scale value to each sample point and use the weighted average of locally estimated functions to define the implicit surface compactly around the input data. The method is virtually parameter-free for mixed-scale datasets and does not require any global operations. Our method draws inspiration from this method and uses scale value computed from the triangulated depth maps to handle the noise outliers.

Fig. 3.

Our point denoising pipeline: we examine a reference point p against other depth maps. A depth map $D_{i}$ is trianglated in the image space. Then we project the reference point to the depth map and get which triangle it falls into. If no such triangle exist, we do not compute any function and examine p against next depth map. If it falls into an triangle, we regard the three vertexes as the neighbor of p and use them to evaluate our functions. Our functions are related to the scale of the points. After examining the reference point against all the depth maps, we compare the functions with threshold and decide if the point will be removed.

3 Denoising and Outlier Removal

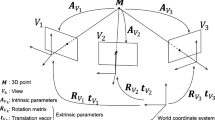
In this section, we describe the evaluation of geometric and photometric consistency between a reference point p and its neighbors in spatial space. We assume that M input depth maps are given and points in them are equipped with a position, a normal and a color.

3.1 Definition of Scale

We define a scale value for each point related to the depth map it comes from. As illustrated in Fig. 3, we first find the adjacent points for a point in the input depth map in image space, and then computed a scale value for each point by averaging the spatial distances between the point and its adjacent points. As discussed by Fuhrmann et al. [3], the scale value provides valuable information about the surface area each point was acquired from. The points in depth maps are not ideal points. Instead, they represent a surface at a particular scale depending on viewing distance, focal length and image resolution [3] as illustrated in Fig. 2. With scale information, we can define local adaptive functions for geometric consistency and photometric consistency to handle datasets containing non-uniform noise and sample resolution.

3.2 Neighbors in Image Space and LCS

To determine the geometric and photometric consistency, every reference point p has to be examined against its neighbors in the spatial space. Depth maps can provide us with additional information such as connectivity. As illustrated in Fig. 3, We triangulate the depth maps in image space using the method proposed by [3]. Then we project the reference point p to other depth maps and get the triangles it falls into. The three vertices of the triangle are regarded as the neighbors of the reference point. After the whole projection, we get a set of neighbors $N_\mathbf{p }=\{\mathbf{p }_{i}|i=1,...,M\}$ for p. Each of them are equipped with a position $\mathbf p _{i}\in \mathbb {R}^{3}$, a normal $\mathbf n _{i}\in \mathbb {R}^{3}$, $\Vert \mathbf n _{i}\Vert =1$, and a scale value $s_{i}\in \mathbb {R}$. Generally, such neighbors are most likely near the reference point in spatial space. Since our functions are compactly supported, we can ensure that the neighbor points used to evaluate geometric and photometric consistency are actually near the reference point. When examining p against $\mathbf p _{i}$, we use the local coordinate of p in the local coordinate system (LCS) of $\mathbf p _{i}$. The local coordinate is $\mathbf x _{i}=R_{i}\cdot (\mathbf p -\mathbf p _{i})$ with a rotation matrix $R_{i}=R(\mathbf n _{i})$ such that $\mathbf p _{i}$ is located in the origin and the normal $\mathbf n _{i}$ coincides with the positive x-axis [4]. The LCS is only up to the position and normal of $\mathbf p _{i}$ so the functions should be invariant to the choice of the LCS orthogonal to the normal.

3.3 Geometric Consistency

Given a reference point p, and a set of neighbors $N_\mathbf{p }=\{\mathbf{p }_{i}|i=1,...,M\}$, we define a signed geometric consistency function $F(\mathbf p )$ as a weighted sum of basis functions, as proposed in the surface reconstruction method [4]:

$$\begin{aligned} F(\mathbf p )=\frac{\sum _{i}wd_{i}(\mathbf x _{i})wn_{i}(\mathbf p _{i}) f_{i}(\mathbf x _{i})}{\sum _{i}wd_{i}(\mathbf x _{i})wn_{i}(\mathbf p _{i})} \end{aligned}$$

$$\begin{aligned} W(\mathbf p )=\sum _{i}wd_{i}(\mathbf x _{i})wn_{i}(\mathbf p _{i}) \end{aligned}$$

(1)

where $\mathbf x _{i}$ is the local coordinate of p in local coordinate system of (LCS) $\mathbf p _{i}$. The basis function $f_{i}(\mathbf x _{i})$ is a signed function which is positive in front of the surface and negative otherwise (similar to a signed distance function). The function $f_{i}(\mathbf x _{i})$ and weight $wd_{i}(\mathbf x _{i})$, $wn_{i}(\mathbf p _{i})$ are parameterized by the ith neighbor’s position $\mathbf p _{i}$, normal $\mathbf n _{i}$ and scale $s_{i}$. Similar to [4], for each neighbor $\mathbf p _{i}$, we define a basis function that is unit-integral and stretched depending on the scale of the neighbor.

With $\mathbf x _{i}=(x,y,z)$, we use a function $f_{x}(x)$ that is like the derivative of the Gaussian in the x-coordinate. The standard deviation of $f_{x}(x)$ is set to the scale of the neighbor, that is $\sigma =s_{i}$. It is positive when $x>0$ and negative when $x<0$. Normalized Gaussians $f_{y}(y)$, $f_{z}(z)$ are used orthogonal to the normal in y-coordinate and z-coordinate.

$$\begin{aligned} f_{x}(x)=\frac{x}{\sigma ^{2}}e^{\frac{-x^{2}}{2\sigma ^{2}}}, f_{y}(y)=\frac{1}{\sigma \sqrt{2\pi }}e^{\frac{-y^{2}}{2\sigma ^{2}}}, f_{z}(z)=\frac{1}{\sigma \sqrt{2\pi }}e^{\frac{-z^{2}}{2\sigma ^{2}}} \end{aligned}$$

(2)

We define the basis function of the ith neighbor as:

$$\begin{aligned} f_{i}(\mathbf x _{i})=f_{x}(x)f_{y}(y)f_{z}(z)=\frac{x}{\sigma ^{4}2\pi }\cdot e^{\frac{-1}{2\sigma ^{2}}(x^{2}+y^{2}+z^{2})} \end{aligned}$$

(3)

The function meets the condition that it must be unit-integral as discussed before:

$$\begin{aligned} \int \int \int |f_{i}(\mathbf x _{i})|d\mathbf x _{i}=\int |f_{x}(x)|dx\int f_{y}(y)dy\int f_{z}(z)dz=1 \end{aligned}$$

(4)

In the following, we define a weighting function $wd_{i}(\mathbf x _{i})$ related to the distance between the neighbor $\mathbf p _{i}$. It is designed to ensure that the neighbor used to evaluate $F(\mathbf p )$ are actually near the reference point p. As illustrated in the Fig. 2, $f_{i}(\mathbf x _{i})$ is almost zero beyond $3\sigma$, and thus $wd_{i}(\mathbf x _{i})$ is define as 0 beyond $3\sigma$ to ensure the compact support. As discussed by Curless and Levoy [1] and Vrubel et al. [14]: if a point has been observed, the existence of a surface between the observer and the point is not possible. Therefore, if $x<0$, the existence of a reference point behind the neighbor cause conflict. Therefore, we want to reduce the weight quickly. The weighting function $wd_{i}(\mathbf x _{i})$ is non-symmetric in x-direction and rotation invariant in y- and z-direction:

$$\begin{aligned} wd_{i}(\mathbf x _{i})=w_{x}(x)\cdot w_{(yz)}(\sqrt{y^{2}+z^{2}}) \end{aligned}$$

(5)

$$\begin{aligned} w_{x}(x)= \left\{ \begin{array}{lr} \frac{1}{9}\frac{x^{2}}{\sigma ^{2}}+\frac{2}{3}\frac{x}{\sigma }+1&{} x\in [-3\sigma ,0)\\ \frac{2}{27}\frac{x^{3}}{\sigma ^{3}}-\frac{1}{3}\frac{x^{2}}{\sigma ^{2}}+1&{} x\in (0,3\sigma ]\\ 0&{}\text {otherwise} \end{array} \right. \end{aligned}$$

(6)

$$\begin{aligned} w_{yz}(r)= \left\{ \begin{array}{lr} \frac{2}{27}\frac{r^{3}}{\sigma ^{3}}-\frac{1}{3}\frac{r^{2}}{\sigma ^{2}}+1&{} r<3\sigma \\ 0&{}\text {otherwise} \end{array} \right. \end{aligned}$$

(7)

$$\begin{aligned} r=\sqrt{y^{2}+z^{2}} \end{aligned}$$

(8)

Additionally, to better preserve the sharp features in the point set and avoid over smoothing, we define a weighting function $wn_{i}(\mathbf p _{i})$ related to the similarity between the normals of the points.

$$\begin{aligned} wn_{i}(\mathbf p _{i})= \left\{ \begin{array}{lr} \frac{\mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}}{\Vert \mathbf{n }_\mathbf{p }\Vert \cdot \Vert \mathbf{n }_{i}\Vert }&{} \mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}>0\\ 0&{}\mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}\le 0 \end{array} \right. \end{aligned}$$

(9)

We define $wn_{i}(\mathbf p _{i})$ as 0 if $\mathbf n ^{T}_\mathbf{p }{} \mathbf n _{i}\le 0$ to eliminate the influence of neighbors that have a much different normal direction with the reference point, which can improve the robustness.

Since $F(\mathbf p )$ is compactly supported, some extremely isolated outliers with little neighbors will have small $F(\mathbf p )$. They cannot be filtered if we only make use of $F(\mathbf p )$. We observe that if a reference point is an outlier with little neighbors, its $W(\mathbf p )$, the sum of the weighting function, will be very small. In practice, points with a weight below a certain value are also removed, which can filter out extremely isolated outliers.

3.4 Photometric Consistency

In practice, our algorithm can filter out common noise and outliers with geometric consistency function. However, as illustrated by Fig. 1(b) (c), the noisy points near the border of object are hard to remove. Our observation is that such points usually have a blurred color that is quite different from its neighbors. So we define a function $E(\mathbf p )$ to evaluate the photometric consistency between the reference point p, with a color $\mathbf c (\mathbf p )$, and its neighbors $N_\mathbf{p }=\{\mathbf{p }_{i}|i=1,...,M\}$, whose colors are $\mathbf c (\mathbf p _{i})$. $E(\mathbf p )$ is defined as

$$\begin{aligned} E(\mathbf p )=\frac{\Vert \mathbf c (\mathbf p )-\mathbf c '(\mathbf p )\Vert }{\Vert \mathbf c (\mathbf p )\Vert } \end{aligned}$$

(10)

where $\mathbf c '(\mathbf p )$ is the temporary color of p computed by the color of its neighbors. Inspired by the anisotropic and feature-preserving nature of bilateral filtering [2], we compute $\mathbf c '(\mathbf p )$ as

$$\begin{aligned} \mathbf c '(\mathbf p )=K(\mathbf p )\sum _{i}W_{c}(\mathbf p _{i})W_{s}(\mathbf p _{i})\mathbf c (\mathbf p _{i}) \end{aligned}$$

(11)

where $W_{c}(\mathbf p _{i})$ is the spatial weighting term, $W_{s}(\mathbf p _{i})$ is the signal weighting term and $K(\mathbf p )=\frac{1}{\sum _{i}W_{c}(\mathbf p _{i})W_{s}(\mathbf p _{i})}$ is the normalization factor. $W_{c}(\mathbf p _{i})$ is a spatial Gaussian that decreases the influence of distant neighbors:

$$\begin{aligned} W_{c}(\mathbf p _{i})=\text {exp}(-\Vert \mathbf p -\mathbf p _{i}\Vert ^{2}/2\sigma ^{2}) \end{aligned}$$

(12)

where $\sigma =s_\mathbf{p }$, which is the scale value of the reference point p. We do not define $W_{s}(\mathbf p _{i})$ as Gaussian but just use the normalized dot product of the normals between $\mathbf p$ and $\mathbf p _{i}$ for efficiency.

$$\begin{aligned} W_{s}(\mathbf p _{i})= \left\{ \begin{array}{lr} \frac{\mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}}{\Vert \mathbf{n }_\mathbf{p }\Vert \cdot \Vert \mathbf{n }_{i}\Vert }&{} \mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}>0\\ 0&{}\mathbf{n }^{T}_\mathbf{p }\mathbf{n }_{i}\le 0 \end{array} \right. \end{aligned}$$

(13)

The influence of neighbors that have a much different normal direction with the reference point, i.e. $\mathbf n ^{T}_\mathbf{p }{} \mathbf n _{i}\le 0$, are eliminated.

3.5 Depth Map Selection for Scalability

Our algorithm proposed above does not perform costly optimizations and thus is very efficient and easy to parallel. However, assuming we have N input depth maps with a resolution of K, the time complexity of our algorithm is $O(KN^{2})$. It increases quadratically with the number of depth maps N. In practice, we do not consider depth maps whose viewing direction $\mathbf v _{i}$ differs too much from the viewing direction $\mathbf v$ under which p was observed, i.e. $\mathbf v _{i}^{T}{} \mathbf v <0$. However, the time complexity still increase quickly when operating extremely large data sets. In order to make our algorithm more scalable, we introduce a view selection method as an option when operating on large data sets. We use SFM points to select nearby depth maps for a reference depth map. The number of shared SFM points between the reference depth map and other depth maps is a good indicator whether the reference point is visible in other depth maps. We calculate the number of shared feature points, sort them from large to small and only examine the points in the reference depth map against the first C depth maps. Now the time complexity is O(KCN), increasing linearly with the number of depth maps N. Since the reference point is not likely visible by the depth maps with few shared SFM points, our algorithm still yields good results with view selection in our experiments.

3.6 Point Filtering Strategy

After evaluating $F(\mathbf p )$, $W(\mathbf p )$ and $E(\mathbf p )$ for a reference point p, we use them to decide whether the point p will be retained. We retain a point if it satisfies all of the following three conditions:

$$\begin{aligned} -T_\mathbf{p }<F(\mathbf p )<T_\mathbf{p },\quad W(\mathbf p )>\alpha ,\quad E(\mathbf p )<\varepsilon \end{aligned}$$

(14)

Since $F(\mathbf p )$ is an locally adaptive function, we define a locally adaptive threshold $T_\mathbf{p }=\beta F(x=s_\mathbf{p },\sqrt{y^{2}+z^{2}}=s_\mathbf{p },\sigma =s_\mathbf{p })$ for $F(\mathbf p )$. Actually, $F(x=s_\mathbf{p },\sqrt{y^{2}+z^{2}}=s_\mathbf{p },\sigma =s_\mathbf{p })$ is the function value of a virtual point whose local coordinates are relate to the scale of reference point. This definition can ensure the adaptivity of filtering. $\beta$ is a constant decided by users to control the degree of filtering. It performs well in feature preserving in our experiments. The threshold of $W(\mathbf p )$ is a constant $\alpha$ to filter out the extremely isolated outliers. It is related to the number of input depth maps and typically we set it to 25 when there are hundreds of input depth maps. The threshold of $E(\mathbf p )$ is a constant $\varepsilon$. We typically set it to 0.1, that is, if the difference between the real color and the temporary color is above $10\%$, we filter the point out. It performs well in eliminating the color blur in the point sets.

4 Results

In this section, we perform evaluation of our algorithm on different types of datasets. In Sect. 4.1 we compare our filtering results with the method proposed by Wolff et al. [17] on several datasets released by Yücer et al. [15]. We use (Screened) Poisson Surface Reconstruction (PSR) [9] for surface reconstruction. In Sect. 4.2 we analyze the performance of our strategy for filtering using the Fountain data set of Strecha et al. [12]. In Sect. 4.3 we check the validity of the photometric consistency function on the Temple Full dataset from the Middlebury benchmark [11].

4.1 Comparison Against the Method of Wolff et al.

Figure 4 shows the results of comparison of our method and the method proposed by Wolff et al. [17] on the datasets released by Yücer et al. [15]. Wolff et al. [17] also takes depth maps as input and use these datasets for the evaluation of their method. We use two of state-of-the-art multi-view stereo methods, the colmap of Schönberger et al. [10] and the MVE of Fuhrmann et al. [5] for the dense multi-view depth reconstruction. While Fuhrmann et al. (MVE) [5] do not integrate a fusion step into the MVS reconstruction, colmap of Schönberger et al. [10] fuse their resulting depth maps into a point cloud. In our experiment, we disable the fusion step in colmap [10] and use its raw depth maps for filtering. We also show the result of the fusion result of colmap [10] for comparison.

We use about 200 input images for the reconstructions of each dataset. For MVE we used the level-2 depth maps (4*downsampling) the same as the experiments of Wolff et al. [17]. We also limit the max image size in colmap to the same resolution as the experiment of MVE for comparison. We run PSR for each point cloud in our experiment after the filtering. As shown in Fig. 4, the outliers of the results of MVE and colmap are very dense so that it is not easy to filter them out. However, our method employ both the $F(\mathbf p )$ and $W(\mathbf p )$ in Geometric consistency and thus more robust to such outliers. Comparing to the results of Wolff et al. [17], we get more clean and dense point cloud and little outliers with our method. In all the experiments, the run time of our method and Wolff et al. are almost the same. With the use of scale value, our method are not only perform well in removing outliers but also preserve more sharp features in the point cloud. Since the method of Wolff et al. are actually global, the results of it often retains some outliers while destroying the sharp features.

Fig. 4.

We use the MVE [5] and colmap [10] to generate the depth maps. After filtering, we use (PSR) [9] to reconstruct a surface for the point cloud. We compare our output point clouds and surfaces with those of Wolff et al. [17]. We also show the result of the fusion method of colmap as a comparison.

4.2 Analysis of Filtering Strategy

In this section, we analyze the filtering strategy of our methods using the datasets released by Yücer et al. [15] and the Fountain data set of Strecha et al. [12]. In our experiments, we use the locally adaptive threshold for $T_\mathbf{p }$. As is shown in Fig. 4, the result of locally adaptive threshold is more clean nearby the surface of the objects. That is, $F(\mathbf p )$ with a locally adaptive threshold performs better in feature preserving with the scale information. We also use different constant threshold of $\alpha$ for $W(\mathbf p )$. As illustrated by Fig. 5, as the increase of $\alpha$, the number of outliers in the point cloud decreases quickly because $W(\mathbf p )$ play an important role in extreme outliers removing.

4.3 Performance of Photometric Consistency

Figure 1 shows the importance of photometric consistency function. The Temple Full dataset from the Middlebury benchmark [11] contains 312 images. Their background are black, so as shown in Fig. 1, the resulting point cloud using MVE contains a mass of black points near the border of the object. These black points are retained when we only apply the photometric consistency. When we integrate the photometric consistency in filtering, most of the black points are removed and the colors of the surface of the object are more uniform.

Fig. 5.

The sum of weight, $W(\mathbf p )$ performs an important role in outliers removing. The $\alpha$ for $W(\mathbf p )$ in (b), (c), (d), (e) are 0, 2, 4, 6. It is clear that as the increase of $\alpha$, the number of outliers decreases quickly.

5 Conclusions

We propose a very efficient point cloud denoiser which is locally adaptive. We are mainly inspired by the surface reconstruction method [4]. Since scale and efficiency are common topics in 3D reconstruction, we hope that other people can be inspired by our work and solve some other problems.