Abstract
General Relativity offers the possibility to model attributes of matter, like mass, momentum, angular momentum, spin, chirality etc. from pure space, endowed only with a single field that represents its Riemannian geometry. I review this picture of ‘Geometrodynamics’ and comment on various developments after Einstein.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
‘Es muß also entweder das dem Raume zugrude liegende Wirkliche eine diskrete Mannigfaltigkeit bilden, oder der Grund der Maßverhältnisse außerhalb, in darauf wirkenden bindenden Kräften gesucht werden.’ (Riemann 1869/1919, 20)
- 2.
Due to the standard convention that the Hamiltonian action is defined as a left action, whereas the Lie bracket on a group is defined by the commutator of left-invariant vector fields which generate right translations.
- 3.
In this article, we use ‘iff’ as abbreviation for ‘if and only if’.
- 4.
The maximal cone touches the three 2-planes λ i = 0 at the bisecting lines λ j = λ k , where i, j and k are any of the three cyclic permutations of 1, 2 and 3. Hence the cosine of the opening angle is the scalar product between \((1,1,1)\sqrt {3}\) and, say, \((1,1,0)\sqrt {2}\), which is \(\sqrt {2/3}\).
- 5.
Had we done the very same analysis in terms of π rather than K, we would have found that in eigenvalue space (now of the endomorphism \(\tilde \pi \)) the opening angle of the cone inside which the bilinear form is negative definite and outside which it is positive definite is now precisely the maximal one \(\arccos (\sqrt {2/3})\) (see previous footnote). Indeed, rewriting the bilinear form in terms of π using (12.18), it is positively proportional to \({\mbox{tr}}(\tilde \pi ^2)-\frac {1}{2}({\mbox{tr}}(\tilde \pi ))^2\). It is the one-half in front of the second term that causes this interesting coincidence.
- 6.
Note that the definition of the ADM mass (12.23) just depends on the Riemannian metric h and is independent of K. But for the theorem to hold, it is essential to require that h is such that there exists a K so that (h and K) satisfy the constraints. It is easy to write down metrics h with negative mass: Take, e.g. (12.29) with negative m for r > r ∗ > m∕2, smoothly interpolated within m∕2 < r < r ∗ to, say, the flat metric in r < m∕2. The positive mass theorem implies that for such a metric, no K can be found so that (h and K) satisfy the constraints.
- 7.
- 8.
That K is Killing is immediate, since (12.33) shows that ρ depends only on the combination X 2 − T 2 which is clearly annihilated by K.
- 9.
The \({\mathbb {R}\mathrm {P}}^3\) geon is different from the two mutually different ‘elliptic interpretations’ of the Kruskal spacetime discussed in the literature by Rindler, Gibbons, and others. In Rindler (1965) the identification map considered is J′ : (T, X, θ, φ)↦(−T, −X, θ, φ), which gives rise to singularities on the set of fixed-points (a 2-sphere) T = X = 0. Gibbons (1986) takes J″ : (T, X, θ, φ)↦(−T, −X, π − θ, φ + π), which is fixed-point free, preserves the Killing field (12.37) (which our map J does not), but does not preserve time-orientation. J″ was already considered in (Misner and Wheeler 1957, section 4.2), albeit in isotropic Schwarzschild coordinates already mentioned above, which only cover the exterior regions I and III of the Kruskal manifold.
- 10.
One uses the Killing identity
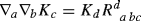 to convert the second derivatives of K
♭ into terms involving no derivatives and the Riemann tensor.
to convert the second derivatives of K
♭ into terms involving no derivatives and the Riemann tensor. - 11.
That is, linear momentum has the unit of length (like mass) and angular momentum of length-squared. They are converted into ordinary units through multiplication with c∕G.
- 12.
The distinction between electric and magnetic is conventional in Einstein-Maxwell theory without sources for the Maxwell field, since the energy-momentum tensor T for the latter is invariant under duality rotations which rotate between F and ⋆ F according to ω↦e(iφ) ω, where ω := F + i ⋆ F. Since
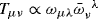 , where an overbar denotes complex conjugation, the invariance of T is immediate.
, where an overbar denotes complex conjugation, the invariance of T is immediate. - 13.
A classic theorem on finite abelian groups states that if pandq are integers, \({\mathbb {Z}}_{pq}\) is isomorphic to \({\mathbb {Z}}_p\oplus {\mathbb {Z}}_q\) iff p and q are coprime.
- 14.
This follows in two steps: First, one recalls \(H^2(Q,{\mathbb {Z}})\) is isomorphic to the direct sum of the free part of \(H_2(Q,{\mathbb {Z}})\) and the torsion part of \(H_1(Q,{\mathbb {Z}})\) (universal coefficient theorem). Second, one uses that \(H_1(Q,{\mathbb {Z}})\) is isomorphic to the abelianisation of the fundamental group (Hurewicz’ theorem).
- 15.
To decide this entails some subtle issues, like whether to diffeomorphisms that are homotopic (continuously connected through a one-parameter family of continuous maps) are also isotopic (continuously connected through a one-parameter family of homeomorphisms) and then also diffeotopic (continuously connected through a one-parameter family of diffeomorphims). The crucial question is whether homotopy implies isotopy, which is not at all obvious since on a homotopy the interpolating maps connecting two diffeomorphism are just required to be continuous, that is, they need not be continuously invertible as for an isotopy. For example, the inversion I(x) = −x in \({\mathbb {R}}^n\) is clearly not isotopic to the identity, but homotopic to it via ϕ t (x) = (1 − 2t)x for t ∈ [0, 1]. Then ϕ 0 = id, ϕ 1 = I and only at t = 1∕2 does the map ϕ t cease to be invertible.
- 16.
The definition of lens spaces L(p, q) in three dimensions is
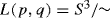 , where (p, q) is a pair of positive coprime integers with p > 1, \(S^3=\{(z_1,z_2)\in {\mathbb {C}}^2\mid \vert z_1\vert ^2+\vert z_2\vert ^2=1\}\), and \((z_1,z_2)\sim (z^{\prime }_1,z^{\prime }_2)\Leftrightarrow z^{\prime }_1={\mbox{e}}(2\pi i/p)z_1\), and \(z^{\prime }_2={\mbox{e}}(2\pi i\,q/p)z_2\). One way to picture the space is to take a solid ball in \({\mathbb {R}}^3\) and identify each points on the upper hemisphere with points on the lower hemisphere after a rotation by 2πq∕p about the vertical symmetry axis. In this way, each set of p equidistant points on the equator is identified to a single point. The fundamental group of L(p, q) is \({\mathbb {Z}}_p\), i.e. independent of q, and the higher homotopy groups are those of its universal cover, S
3. This does, however, not imply that L(p, q) is homotopy equivalent, or even homeomorphic, to L(p, q). The precise relation will be stated below.
, where (p, q) is a pair of positive coprime integers with p > 1, \(S^3=\{(z_1,z_2)\in {\mathbb {C}}^2\mid \vert z_1\vert ^2+\vert z_2\vert ^2=1\}\), and \((z_1,z_2)\sim (z^{\prime }_1,z^{\prime }_2)\Leftrightarrow z^{\prime }_1={\mbox{e}}(2\pi i/p)z_1\), and \(z^{\prime }_2={\mbox{e}}(2\pi i\,q/p)z_2\). One way to picture the space is to take a solid ball in \({\mathbb {R}}^3\) and identify each points on the upper hemisphere with points on the lower hemisphere after a rotation by 2πq∕p about the vertical symmetry axis. In this way, each set of p equidistant points on the equator is identified to a single point. The fundamental group of L(p, q) is \({\mathbb {Z}}_p\), i.e. independent of q, and the higher homotopy groups are those of its universal cover, S
3. This does, however, not imply that L(p, q) is homotopy equivalent, or even homeomorphic, to L(p, q). The precise relation will be stated below. - 17.
As regards the notion of chirality, an interesting refinement of this statement is that L(p, q) and L(p, q′) are orientation-preserving homeomorphic iff q′ = q ±1 (mod p) (Reidemeister 1935).
- 18.
Maxwell equations were thought of as a kind of effective theory that describes things on a coarse-grained scale, so that, e.g. the vortex knots could be approximated by point particles.
References
Arnowitt, R., Deser, S., & Misner C. W. (1962). The dynamics of general relativity. In L. Witten (Ed.), Gravitation: An introduction to current research (pp. 227–265). New York and London: Wiley.
Beig, R., & Ó Murchadha, N. (1987). The Poincaré group as symmetry group of canonical general relativity. Annals of Physics, 174, 463–498.
Bott, R., & Tu, L. W. (1982). Differential forms in algebraic topology. Graduate texts in mathematics. New York: Springer.
Clifford, W. K. (1982). Mathematical Papers (1st ed.). London: Macmillan (1882). R. Tucker (Ed.)
Deser, S. (1988). Absence of regular static Einstein solutions in arbitrary dimensions. Classical and Quantum Gravity, 5(1), L9–L10.
DeWitt, B. (1967). Quantum theory of gravity I. Physical Review, 160, 1113–1148.
Dowker, F., & Sorkin, R. (1998). A spin-statistics theorem for certain topological geons. Classical and Quantum Gravity, 15, 1153–1167.
Dowker, F. & Sorkin, R. (2000). Spin and statistics in quantum gravity. In R. C. Hilborn & G. M. Tino (Eds.), Spin-statistics connections and commutation relations: experimental tests and theoretical implications (pp. 205–218). New York: American Institute of Physics.
Ebin, D. G. (1968). On the space of Riemannian metrics. Bulletin of the American Mathematical Society, 74(5), 1001–1003.
Einstein, A. (1920). Äther und Relativitätstheorie. Reprinted in M. Jannsen, et al. (Eds.), The collected papers of Albert Einstein, volume 7 (pp. 306–320). Princeton, NJ: Princeton University Press.
Einstein, A., & Pauli W. (1943). On the non-existence of regular stationary solutions of relativistic field equations. Annals of Mathematics, 44(2), 131–137.
Finkelstein, D., & Rubinstein, J. (1968). Connection between spin, statistics, and kinks. Journal of Mathematical Physics, 9(11), 1762–1779.
Fischer, A. E. (1970). The theory of superspace. In M. Carmeli, S.I. Fickler, L. Witten (Eds.), Relativity. Proceedings of the Relativity Conference in the Midwest, held June 2–6, 1969, at Cincinnati Ohio (pp. 303–357). New York: Plenum Press.
Fischer, A. E. (1986). Resolving the singularities in the space of Riemannian geometries. Journal of Mathematical Physics, 27, 718–738.
Friedman, J., & Mayer, S. (1982). Vacuum handles carrying angular momentum; electrovac handles carrying net charge. Journal of Mathematical Physics, 23(1), 109–115.
Friedman, J., & Sorkin, R. (1980). Spin 1/2 from gravity. Physical Review Letters, 44, 1100–1103.
Gannon, D. (1975). Singularities in nonsimply connected space-times. Journal of Mathematical Physics, 16(12), 2364–2367.
Gibbons, G. W. (1968). The elliptic interpretation of black holes and quantum mechanics. Nuclear Physics, B, 98, 497–508.
Gilbert, N. D. (1987). Presentations of the automorphims group of a free product. Proceedings of the London Mathematical Society, 54, 115–140,
Giulini, D. (1990) Interaction energies for three-dimensional wormholes. Classical and Quantum Gravity, 7(8), 1272–1290.
Giulini, D. (1993). On the possibility of spinorial quantization in the Skyrme model. Modern Physics Letters A, 8(20), 1917–1924.
Giulini, D. (1994). 3-manifolds for relativists. International Journal of Theoretical Physics, 33, 913–930.
Giulini, D. (1995a). On the configuration-space topology in general relativity. Helvetica Physica Acta, 68, 86–111.
Giulini, D. (1995b). Quantum mechanics on spaces with finite fundamental group. Helvetica Physica Acta, 68, 439–469.
Giulini, D. (1995c). What is the geometry of superspace? Physical Review D, 51(10), 5630–5635.
Giulini, D. (1997). The group of large diffeomorphisms in general relativity. Banach Center Publications, 39, 303–315.
Giulini, D. (2007). Mapping-class groups of 3-manifolds in canonical quantum gravity. In B. Fauser, J. Tolksdorf, & E. Zeidler (Eds.), Quantum gravity: Mathematical models and experimental bounds. Basel: Birkhäuser Verlag. Online available at 〈arxiv.org/pdf/gr-qc/0606066〉.
Giulini, D. (2008). Concepts of symmetry in the work of Wolfgang Pauli. In H. Atmanspacher & H. Primas (Eds.), Recasting reality. Wolfgang Pauli’s philosophical ideas and contemporary science (pp. 33–82). Berlin: Springer. Online available at 〈arxiv.org/pdf/0802.4341v1〉.
Giulini, D. (2009). The superspace of geometrodynamics. General Relativity and Gravitation, 41(4), 785–815.
Gross, D., & Perry, M. (1983). Magnetic monopoles in Kaluza-Klein theories. Nuclear Physics, B, 115, 29–48.
Hawking, S. W., & Ellis, G. F. R. (1973). The large scale structure of spacetime. Cambridge: Cambridge University Press.
Hojman, S. A., Kuchař, K., & Teitelboim, C. (1973). New approach to general relativity. Nature Physical Science, 245, 97–98.
Hojman, S. A., Kuchař, K., & Teitelboim, C. (1976). Geometrodynamics regained. Annals of Physics, 96, 88–135.
Kazdan, J. L., & Warner, F. W. (1975). Scalar curvature and conformal deformation of Riemannian structure. Journal of Differential Geometry, 10(1), 113–134.
Komar, A. (1959). Kovariant conservation laws in general relativity. Physicsl Review, 113(3), 934–936.
Kruskal, M. D. (1960). Maximal extension of Schwarzschild metric. Physical Review, 119(5), 1743–1745.
Kuchař, K. (1973). Geometrodynamics regained: A Lagrangian approach. Journal of Mathematical Physics, 15(6), 708–715.
Lichnerowicz, A. (1955). Théories Relativistes de la Gravitation et de l’Électromagnétisme. Masson et Cie, Paris, 1955.
McCarty, G. C., & Shultz, G. (1963). Homeotopy groups. Transactions of the American Mathematical Society, 106, 293–303.
Misner, C. (1959). Wormhole initial conditions. Physical Review, 118(4), 1110–1111 (1959).
Misner, C. (1963). The method of images in geometrostatics. Annals of Physics, 24, 102–117.
Misner, C., Thorne, K. S., & Wheeler, J. A. (1973). Gravitation. New York: W.H. Freeman and Company.
Misner, C., & Wheeler, J. A. (1957). Classical physics as geometry: Gravitation, electromagnetism, unquantized charge, and mass as properties of curved empty space. Annals of Physics, 2, 525–660.
Müllner, D. (2008). Orientation Reversal of Manifolds. PhD thesis, Friedrich-Wilhelms-Universität Bonn, October (2008).
Pesic, P. (Ed.), (2007). Beyond geometry. Classic papers from Riemann to Einstein. Mineola, NY: Dover Publications, Inc.
Reidemeister, K. (1935). Homotopieringe und Linsenräume. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, 11(1), 102–109.
Riemann, B. (1869/1919). Über die Hypothesen, welche der Geometrie zu Grunde liegen (1869), (2nd ed.) (1919), Edited and annotated by H. Weyl. Berlin: Springer.
Rindler, W. (1965). Elliptic Kruskal-Schwarzschild space. Physical Review Letters, 15(26), 1001–1002.
Skyrme, T. H. R. (1971). Kinks and the Dirac equation. Journal of Mathematical Physics, 12(8), 1735–1743.
Sorkin, R. (1977). On the relation between charge and topology. Journal of Physics A: Mathematical and General, 10(5), 717–725.
Sorkin, R. (1983). Kaluza-Klein monopole. Physical Review Letters, 51(2), 87–90.
Sorkin, R. (1988). A general relation between kink-exchange and kink-rotation. Communications in Mathematical Physics, 115, 421–434.
Teitelboim, C. (1973). How commutators of constraints reflect the spacetime structure. Annals of Physics, 79(2), 542–557.
Whitehead, J. H. C. (1941). On incidence matrices, nuclei and homotopy types. Annals of Mathematics, 42(5), 1197–1239.
Witt, D. (1986). Symmetry groups of state vectors in canonical quantum gravity. Journal of Mathematical Physics, 27(2), 573–592.
Woodhouse, N. (1991). Geometric quantization (2nd ed.). Oxford: Clarendon Press.
Acknowledgements
I sincerely thank the organisers of the Beyond Einstein conference at Mainz University for inviting me to this most stimulating and pleasant meeting.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Science+Business Media, LLC, part of Springer Nature
About this chapter
Cite this chapter
Giulini, D. (2018). Matter from Space. In: Rowe, D., Sauer, T., Walter, S. (eds) Beyond Einstein. Einstein Studies, vol 14. Birkhäuser, New York, NY. https://doi.org/10.1007/978-1-4939-7708-6_12
Download citation
DOI: https://doi.org/10.1007/978-1-4939-7708-6_12
Published:
Publisher Name: Birkhäuser, New York, NY
Print ISBN: 978-1-4939-7706-2
Online ISBN: 978-1-4939-7708-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


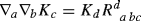 to convert the second derivatives of K
♭ into terms involving no derivatives and the Riemann tensor.
to convert the second derivatives of K
♭ into terms involving no derivatives and the Riemann tensor.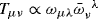 , where an overbar denotes complex conjugation, the invariance of T is immediate.
, where an overbar denotes complex conjugation, the invariance of T is immediate.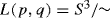 , where (p, q) is a pair of positive coprime integers with p > 1,
, where (p, q) is a pair of positive coprime integers with p > 1,