Abstract
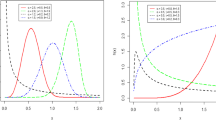
Heavy-tailed distributions are used in various areas of statistical applications. An important parameter for such distributions is the tail coefficient defined as the regular variation coefficient of the inverse cumulative hazard function. Many estimators, among which perhaps the most well known is the Hill estimator, have been developed for this coefficient. However, the Hill estimator as well as improved versions that are based on it rely on asymptotic expansions that are unlikely to hold for small samples. In this paper, we introduce a new approach to the tail coefficient estimation in the case of Weibull-type distributions that works well for small samples. A simulation study is carried out to characterize the properties of the new estimator and shows that it outperforms existing estimators based on asymptotic assumptions in terms of accuracy and the corresponding uncertainty.



Similar content being viewed by others
References
Ahn S, Kim JHT, Ramaswami V (2012) A new class of models for heavy tailed distributions in finance and insurance risk. Insur Math Econ 51(1):43–52
Beirlant J, Teugels J, Vynckier P (eds) (1996) Practical analysis of extreme values. Leuven University Press, Leuven
Beirlant J, Goegebeur Y, Segers J, Teugels J (eds) (2004) Statistics of extremes: theory and applications. Wiley Series in Probability and Statistics, New York
Beran J, Schell D (2012) On robust tail index estimation. Comput Stat Data Anal 56:3430–3443
Broniatowski M (1993) On the estimation of the weibull tail coefficient. J Stat Plann Inference 35:349–366
De Haan L, Peng L (1998) Comparison of tail index estimators. Stat Neerl 52(1):60–70
Embrechts P, Kluppelberg C, Mikosch T (eds) (1997) Modelling extremal events. Springer, Berlin
Felgueiras MM (2012) Explaining the seismic moment of large earthquakes by heavy and extremely heavy tailed models. GEM Int J Geomath 3(2):209–222
Gardes L, Girard S (2005) Estimating extreme quantiles of weibull tail distributions. Commun Stat Theory Methods 34:1065–1080
Gardes L, Girard S (2006) Comparison of weibull tail-coefficient estimators. REVSTAT Stat J 4:163–188
Gardes L, Girard S (2008) Estimation of the weibull tail-coefficient with linear combination of upper order statistics. J Stat Plann Inference 138:1416–1427
Gardiner JC, Luo Z, Tang X, Ramamoorthi RV (2012) Fitting heavy-tailed distributions to health care data by parametric and bayesian methods. J Stat Theory Pract 8(4):619–652
Girard S (2004) A hill type estimator of the weibull tail-coefficient. Commun Stat Theory Methods 33(2):205–234
Goegebeur Y, Beirlant J, De Wet T (2010) Generalized kernel estimators for the weibull-tail coefficient. Commun Stat Theory Methods 39:3695–3716
Hallinan A Jr (1993) A review of the weibull distribution. J Qual Technol 25(2):85–93
Hampel FR, Ronchetti EM, Rousseeuw PJ, Stahel WA (eds) (1986) Robust statistics: the approach based on influence functions. Wiley, New York
Han SW, Busch TM, Mesquita RC, Putt M (2014) A method for choosing the smoothing parameter in a semi-parametric model for detecting change-points in blood flow. J Appl Stat 41(1):26–45
Hill BA (1975) Simple general approach to inference about the tail of a distribution. Ann Stat 3:1163–1173
Huber PJ (ed) (1981) Robust statistics. Wiley, New York
Ibragimov M, Ibragimov R, Walden J (eds) (2015) Heavy-tailed distributions and robustness in economics and finance. Springer International Publishing, Berlin
Mason DM (1982) Laws of large numbers for sums of extreme values. Ann Probab 10(3):754–764
Pisarenko V, Rodkin M (eds) (2010) Heavy-tailed distributions in disaster analysis. Springer, Dordrecht
Rachev ST (ed) (2003) Handbook of heavy tailed distributions in finance, 1st edn. North Holland, Amsterdam
Serfling RJ (ed) (1980) Approximation theorems of mathematical statistics. Wiley, New York
Weibull W (1951) A statistical distribution function of wide applicability. J Appl Mech 18:293–296
Acknowledgements
Part of this work was supported by the African Institute for Mathematical Sciences (AIMS), South Africa. The author Kokouvi Gamado is grateful for funding from the Scottish Government’s RESAS. The authors also thank Prof. Glenn Marion at Biomathematics and Statistics Scotland (BioSS) for helping greatly improve the presentation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kpanzou, T.A., Gamado, K.M. & Hounnon, H. A Beran-Inspired Estimator for the Weibull-Type Tail Coefficient. J Stat Theory Pract 13, 20 (2019). https://doi.org/10.1007/s42519-018-0013-8
Published:
DOI: https://doi.org/10.1007/s42519-018-0013-8