New Exact Solutions of a Perturbed Nonlinear Schrodingers in Nonlinear Optics

Abstract

Here, new exact travelling wave solutions of a perturbed nonlinear Schrodingers equation arising in nonlinear optics are successfully obtained via the generalized Kudryashov method. The proposed method has been successfully implemented to seek exact solutions for the modeles coming for describing nonlinear optics. The results obtained by the generalized Kudryashov method is straightforward and concise mathematical tool to establish the exact analytical solutions of nonlinear equations. The solutions obtained here are new and have not been reported in former literature.

Introduction

The investigation of the travelling wave solutions for nonlinear evolution equations arising in mathematical physics plays an important role in the study of nonlinear physical phenomena. The nonlinear evolution equations are major subjects in physical science,appears in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics and ochemistry. Nonlinear wave phenomena of dissipation, diffusion, reaction and convection are very important in nonlinear wave equations. In the past several decades,new exact solutions may help to find new phenomena. A variety of powerful methods for obtaining the exact solutions of nonlinear evolution equations have been presented [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23].

The nonlinear Schrodinger equation has a central importance in many natural sciences as well as engineering with numerous interpretations and applications concerning e.g. nonlinear optics, protein chemistry, plasma physics and fluid dynamics. This paper will consider the perturbed NLSE which governs the dynamics of solitons in negativeindex material with non-Kerr nonlinearity and third-order dispersion, and the dimensionless form of the equation is given by [24,25,26,27,28,29]

$$\begin{aligned}&iu_{t}+au_{xx}+bu_{xt}+cF(|u|^2)u= -i du_{x}-i s(|u|^2u)_{x}-i\mu (|u|^2)_{x}u-i\theta |u|^2 u_{x}\nonumber \\&\qquad -\,i\gamma u_{xxx}-\theta _{1}(|u|^2u)_{xx}-\theta _{2}|u|^2u_{xx}-\theta _{3}u^2u^{*}_{xx}, \end{aligned}$$

(1)

where u(x, t) is the complex field amplitude. a, b, and c are the coefficients of group velocity dispersion, spatial temporal dispersion and non-Kerr nonlinearity, and d, s, $\mu$, $\theta$ and $\gamma$ account for the inter-modal dispersion, selfsteepening, Raman effect, nonlinear dispersion and third order dispersion, respectively. The last three terms appear in the context of negative-index material.

The main aim of this study is to extract exact solitons to Eq. (1) using the proposed method. Four different kinds of nonlinearity are considered for Eq. (1). They are Kerr law, power law, parabolic law and dual-power law.

Analysis of the Method

In what follows the properties of the the generalized Kudryashov method [30, 31] as:

For a given the general nonlinear partial differential equation of the type

$$\begin{aligned} \psi (u,u_{t},u_{x},u_{xx},u_{tt},\ldots )=0, t>0 \end{aligned}$$

(2)

where u(x, t) is an unknown function, x is the spatial variable and t is the time variable, $\psi$ is a polynomial in u and its derivatives, in which the highest order derivatives and nonlinear terms are involved.

Step 1 The travelling wave variable $\xi =x-\nu t$ transform Eq. (2) into ODE as

$$\begin{aligned} \phi (u,u^{'},u^{'},u^{''},\ldots )=0, \end{aligned}$$

(3)

where the prime denotes to the differenation with respect to $\xi$.

Step 2 Considering trial equation of solution in Eq. (3), it can be written as

$$\begin{aligned} U(\xi )=\frac{\sum _{i=0}^{n}a_{i}Q^{i}(\xi )}{\sum _{j=0}^{m}b_{j}Q^{j}(\xi )}=\frac{A[Q(\xi )]}{B[Q(\xi )]} \end{aligned}$$

(4)

where A and B are polynomial of $Q(\xi )$.

Therefore, we can find the value of N and M, where $Q=Q(\xi )$ satisfies the following ODE:

$$\begin{aligned} Q^{'}(\xi )=Q^2(\xi )-Q(\xi ) \end{aligned}$$

(5)

The Riccati Eq. (5) admits the following exact solution as follows:

$$\begin{aligned} Q_{1}(\xi )= & {} \frac{1}{2}\left[ 1-tanh\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}>0 \end{aligned}$$

(6)

$$\begin{aligned} Q_{2}(\xi )= & {} \frac{1}{2}\left[ 1-coth\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}<0 \end{aligned}$$

(7)

where $\epsilon$ is an constant.

Step 3 The positive integer N and M appearing in Eq. (4) can be determined by considering the balancing between the highest order derivative and the nonlinear term comes from Eq. (2) via the relations

$$\begin{aligned} D\left[ \frac{\partial ^q u}{\partial \xi ^q}\right)= & {} N-M+q,\nonumber \\ D\left. \left[ u^p \left( \frac{\partial ^q u}{\partial \xi ^q)^s}\right) \right) \right.= & {} (N-M)p+s(N-M+q), \end{aligned}$$

(8)

where p, q, s are integer numbers. Therefore, we can find the value of N and M in Eq. (4).

Step 4 Inserting Eq. (4) along Eq. (5) into Eq. (3) and collecting all the terms of the same power $Q^{i}(\xi )$, $(i= 0, 1, 2, \ldots )$ and equating them to zero, we obtain a system of algebraic equations, which can be solved it for obtaning the values $A_{i}$, $B_{j}$, c, $\delta$. Substituting the values in Eq. (4) along with general solutions of Eq. (5) one can directly evaluated the exact solutions of Eq. (9).

The New Exact Solutions of Eq. (1)

To solve Eq. (1), we use the wave transformations as

$$\begin{aligned} u(x,t)=P(\xi )e^{i\phi (x,t)}, \end{aligned}$$

(9)

where $P(\xi )$ represents the shape of the pulse and

$$\begin{aligned} \xi =x-\nu t, \phi (x,t)=-kx+wt+\xi _{0} \end{aligned}$$

(10)

In Eq. (9), $\phi (x,t)$ gives the phase component of the soliton. Then, in Eq. (10), k, w and $\xi _{0}$ respectively represent the frequency, wave number and phase constant and in Eq. (10), v shows the velocity of the soliton.

By using Eq. (9) into Eq. (1) and then decomposing into real and imaginary parts yield a pair of relations. Real part gives

$$\begin{aligned}&(a-b\nu +3k\gamma )P^{''}-((1-bk)w +ak^2-dk+\gamma k^3)P\nonumber \\&\quad +\,cF(P^2)P+(sk +\theta k -\theta _{1}k^2 -\theta _{2} k^2 -\theta _3 k^2)P^3\nonumber \\&\quad +\,6\theta _{1}P(P^{'2})+(3\theta _{1}+\theta _{2}+\theta _{3})P^2P^{''}= 0, \end{aligned}$$

(11)

and the maginary part reads

$$\begin{aligned} (-\nu -2ak+bw+bk\nu +d-3\gamma k^2 )P^{'}+(3s+2\mu +\theta -2k(3 \theta _{1}+\theta _{2}-\theta _{3})P^2P^{'}+\gamma P^{'''}=0 \end{aligned}$$

(12)

From the maginary part, we have

$$\begin{aligned} \gamma =0, \nu =-\frac{2ak-bw-d}{1-bk},\quad 3s+2\mu +\theta -2k(3\theta _{1}+\theta _{2}-\theta _{3})=0 \end{aligned}$$

(13)

With aid of Eq. (13), with $\theta _{1}=0$, $\theta _{2}=-\theta _{3}$ and $s=-\theta$, Eq. (12) yields

$$\begin{aligned} (a-b\nu )P^{''}-((1-bk)w+ak^2-dk)P+cF(P^2)P=0, \end{aligned}$$

(14)

where $\theta -\mu -2\theta _{3}k=0$

For Kerr Law

For Kerr law nonlinearity as $F(q)=q$, then Eq. (14) becomes

$$\begin{aligned} (a-b\nu )P^{''}-((1-bk)w+ak^2-dk)P+cP^3=0 \end{aligned}$$

(15)

In this section the propsed methed will be used for construction the new exact solution of Eq. (15). Now balancing the highest order derivative $P^{''}$ and nonlinear term $P^3$, we get $3N-3M=N-M+2$ or equivalent $N=M+1$. Setting $M=1$, we obtain $N=2$. Then Eq. (14) reads

$$\begin{aligned} P(\xi )=\frac{a_{0}+a_{1}Q(\xi )+a_{2}Q^2(\xi )}{b_{0}+b_{1}Q(\xi )} \end{aligned}$$

(16)

Making use of Eq. (16) into (15) with Eq. (5), and collecting all power of $Q(\xi )$, we get a system of algebraic equations. By solving this algebraic system of equations, we have

case (1)

$$\begin{aligned} k= & {} k,\quad \nu =\frac{(ab_{1}^2+2ca_{1}^2)}{b b_{1}^2},\quad w =\frac{(-dkb_{1}^2+a k^2 b_{1}^2-c a_{1}^2)}{b_{1}^2(-1+bk)},\nonumber \\ a_{0}= & {} 0,\quad a_{1}=a_{1},\quad a_{2}= -2a_{1},\quad b_{0}=0,\quad b_{1}=b_{1} \end{aligned}$$

(17)

case (2)

$$\begin{aligned} k= & {} k,\quad \nu =\frac{(2c a_{0}^2+a b_{0}^2)}{b b_{0}^2},\quad w=\frac{(ak^2 b_{0}^2-c a_{0}^2-d k b_{0}^2)}{b_{0}^2(-1+bk)},\nonumber \\ a_{0}= & {} a_{0},\quad a_{1}=-\frac{(2b_{0}+b_{1} a_{0}}{b_{0}},\quad a_{2}=0,\quad b_{0}=b_{0},\quad b_{1}=b_{1} \end{aligned}$$

(18)

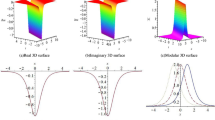
In view of Eq. (17), inserting Eq. (17) into (16), admits to the new exact solution of Eq. (15) as

$$\begin{aligned} P(\xi )= & {} \frac{a_{1}Q(\xi )-2a_{1}Q^2(\xi )}{b_{1}Q(\xi )}, \end{aligned}$$

(19)

$$\begin{aligned} u(x,t)= & {} P(\xi )e^{i\phi (x,t)}, \end{aligned}$$

(20)

$$\begin{aligned} \xi= & {} x-\nu t, \phi (x,t)=-kx+wt+\xi _{0} \end{aligned}$$

(21)

where w, $\nu$ and k are given in Eq. (17),

$$\begin{aligned} Q_{1}(\xi )= & {} \frac{1}{2}\left[ 1-tanh\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}>0 \end{aligned}$$

(22)

$$\begin{aligned} Q_{2}(\xi )= & {} \frac{1}{2}\left[ 1-coth\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}<0 \end{aligned}$$

(23)

Remark 1

it is worth noting the new exact solutions obtained here are new and have not been reported in former literature. For simplicity case (2) should be omitted here.

For Power Law

In this case, we assume as $F(q)=q^ n$, then Eq. (14) becomes

$$\begin{aligned} (a-b\nu )P^{''}-((1-bk)w+ak^2-dk)P+C P^{2n+1}=0 \end{aligned}$$

(24)

In the same manner, to solve for obtaining the exact solution of Eq. (24), we use

$$\begin{aligned} P=u^{\frac{1}{2n}} \end{aligned}$$

(25)

Then Eq. (24) reads

$$\begin{aligned} (a-b\nu )((1-2n) U^{'2} +2nUU^{''})-4n^2((1-bk)w+ak^2-dk)U^2+4c n^2 U^3=0 \end{aligned}$$

(26)

Balancing the highest order derivative $UU^{''}$ and nonlinear term $U^3$, we get $3N-3M=N-M+2$ or equivalent $N=M+2$. For $M=1$, we obtain $N=3$. Then Eq. (26) reads

$$\begin{aligned} U(\xi )=\frac{a_{0}+a_{1}Q(\xi )+a_{2}Q^2(\xi )+a_{3}Q^3(\xi )}{b_{0}+b_{1}Q(\xi )} \end{aligned}$$

(27)

Inserting Eq. (27) into (26) with Eq. (5), and collecting all power of $Q(\xi )$, we get a system of algebraic equations. By solving this algebraic system of equations, we have

case (1)

$$\begin{aligned} k= & {} k,\quad \nu =\nu , \quad w = w,\quad a_{0}=\frac{b_{0}(w-wbk+ak^2-dk)}{c},\nonumber \\ a_{1}= & {} \frac{b_{1}(w-wbk+ak^2-dk)}{c}, \quad a_{0}=0, \quad a_{3} = 0,\nonumber \\ b_{0}= & {} b_{0}, \quad b_{1} = b_{1} \end{aligned}$$

(28)

case (2)

$$\begin{aligned}&\nu =-\frac{(-a+4n^2w-4n^2 w bk+4n^2 ak^2-4n^2d*k)}{b},\nonumber \\&a_{1}=\frac{4b_{0}(-nwbk+nak^2-ndk+nw+w-wbk+ak^2-dk)}{c},\nonumber \\&a_{2}=\frac{-4(-ndkb_{0}-nb_{1}w-nb_{1}a k^2+nb_{1}wbk+nwb_{0}+nb_{1}dk-nwbkb_{0}+nak^2b_{0}-dkb_{0}-wb_{1}-ak^2b_{1}+wbkb_{1}+wb_{0}+dkb_{1} wbkb_{0}+ak^2b_{0}}{c},\nonumber \\&k=k, \quad w=w, \quad a_{0}=0, \quad b_{0}=b_{0},\quad b_{1}=b_{1} \end{aligned}$$

(29)

Using Eq. (28) into (27), one can directly obtined the new exact traveling wave solution as

$$\begin{aligned} U(\xi )= & {} \frac{\frac{b_{0}(w-wbk+ak^2-dk)}{c}+a_{1}Q(\xi )+\left[ \frac{b_{1}(w-wbk+ak^2-dk)}{c}\right] Q^2(\xi )}{b_{0}+b_{1}Q(\xi )}, \end{aligned}$$

(30)

$$\begin{aligned} P= & {} U^{\frac{1}{2n}}, \end{aligned}$$

(31)

$$\begin{aligned} u(x,t)= & {} P(\xi )e^{i\phi (x,t)}, \end{aligned}$$

(32)

$$\begin{aligned} \xi= & {} x-\nu t, \phi (x,t)=-kx+wt+\xi _{0} \end{aligned}$$

(33)

where w, $\nu$ and k are given in Eq. (28),

$$\begin{aligned} Q_{1}(\xi )= & {} \frac{1}{2}\left[ 1-tanh\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \xi _{0}>0 \end{aligned}$$

(34)

$$\begin{aligned} Q_{2}(\xi )= & {} \frac{1}{2}\left[ 1-coth\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \xi _{0}<0 \end{aligned}$$

(35)

Remark 2

The new exact traveling wave solution obtained here via the proposed method are new and have not been reported in former literature. For simplicity case (2) should be omitted here.

For Parabolic Law

Here, we set $F(q)=q+\eta q^2$, then Eq. (14) becomes

$$\begin{aligned} (a-b\nu )P^{''}-((1-bk)w+ak^2-dk)P+cP^3 +c\eta P^{5}=0 \end{aligned}$$

(36)

To solve the reduced Eq. (36) for constructing the new exact solutions of Eq. (36), we use

$$\begin{aligned} P=U^{\frac{1}{2}} \end{aligned}$$

(37)

Then Eq. (36) can be rewritten as

$$\begin{aligned} (a-b\nu )(2UU^{''}-U^{'2})-4((1-bk)w+ak^2-dk)U^2+4cU^3+4c\eta U^4=0 \end{aligned}$$

(38)

Balancing the highest order derivative $UU^{''}$ and nonlinear term $U^4$, we get $N=M+1$ and

$$\begin{aligned} U(\xi )=\frac{a_{0}+a_{1}Q(\xi )+a_{2}Q^2(\xi )}{b_{0}+b_{1}Q(\xi )} \end{aligned}$$

(39)

Inserting Eq. (39) into (38) with Eq. (5), and collecting all power of $Q(\xi )$, we get a system of algebraic equations. By solving this algebraic system of equations, we have

$$\begin{aligned} c= & {} \frac{-3b_{1}^2(w-wbk+ak^2-dk)}{a_{2}\eta },\quad k=k,\nonumber \\ \nu= & {} -\frac{(-4dk-a-4wbk+4ak^2+4w)}{b},\quad w = w, \quad a_{0}=0,\nonumber \\ a_{1}= & {} -a_{2},\quad a_{2}=a_{2},\quad b_{0}=\frac{-1}{8}\frac{b_{1}(4a_{2}\eta -3b_{1})}{a_{2}\eta }, \quad b_{1}=b_{1} \end{aligned}$$

(40)

Making use Eq. (40) into (39), admits to

$$\begin{aligned} U(\xi )= & {} \frac{-a_{2}Q(\xi )+a_{2}Q^2(\xi )}{\frac{-1}{8}\frac{b_{1}(4a_{2}\eta -3b_{1}}{a_{2}\eta }+b_{1}Q(\xi )}, \end{aligned}$$

(41)

$$\begin{aligned} P= & {} U^{\frac{1}{2}}, \end{aligned}$$

(42)

$$\begin{aligned} u(x,t)= & {} P(\xi )e^{i\phi (x,t)}, \end{aligned}$$

(43)

$$\begin{aligned} \xi= & {} x-\nu t, \phi (x,t)=-kx+wt+\xi _{0} \end{aligned}$$

(44)

where w, $\nu$ and k are given in Eq. (40),

$$\begin{aligned} Q_{1}(\xi )= & {} \frac{1}{2}\left[ 1-tanh\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}>0 \end{aligned}$$

(45)

$$\begin{aligned} Q_{2}(\xi )= & {} \frac{1}{2}\left[ 1-coth\left[ \frac{\xi }{2}-\frac{\epsilon ln \xi _{0}}{2}\right] \right] , \quad \xi _{0}<0 \end{aligned}$$

(46)

Remark 3

The new exact solutions Eq. (41) obtained here are new and have not been reported in former literature.

Conclusion and Summary

In this work, we investigated analytically solutions the nonlinear physical model Eq. (1) arising in nonlinear optics vis the generalized Kudryashov method. Different kinds of nonlinearities including Kerr law, power law, parabolic law and dual-power law are taken into accountd.

The generalized Kudryashov method has been successfully implemented to seek exact solutions for nonlinear differential equations coming for describing nonlinear optics. An extended methods will be used such as [32,33,34,35,36,37,38,39,40,41] for constructing the travelling wave solutions of a fractional order space-time nonlinear evolution equations arising in nonlinear optics. This our task in future.

We conclude that the studied method can be more effectively applied to investigate other nonlinear partial differential equations which frequently arise in mathematical physics and other scientific application fields.

To our knowledge, these new solutions have not been reported in former literature, they may be of significant importance for the explanation of some special physical phenomena.