Permissible range of model parameters for natural fine-grained materials

Abstract

This paper presents a three-dimensional constitutive model for natural clay that includes creep, anisotropy and structure, as well as a theoretical means to estimate the range for anisotropy- and structure-related parameters, as needed for parameter optimisation. Creep-SCLAY1S is an extension of the Creep-SCLAY1 model proposed by Sivasithamparam et al. (Comput Geotech 69:46–57, 2015) which includes the effects of bonding and destructuration. The model needs 14 model parameters, of which five are similar to those used in the modified Cam–Clay model. A method is developed to quantify the range for the three parameters related to structure and anisotropy that cannot be derived directly from experimental data. The theoretically derived range compares favourably with the values found in the literature. As a result, the model now can be used with more confidence, enabling sensitivity analysis and systematic parameter derivation with optimisation techniques.

1 Introduction

Modelling of saturated fine-grained matter such as natural soft soils has always been a challenge in engineering. The strain–stress behaviour of these materials is very complex and highly nonlinear. Numerous of different features of soil behaviour, such as time/rate dependency (sometimes called creep), anisotropy as well as bonding/destructuration influence the relation between strain and stress as a function of strain rate. Advanced models taking into account these different features are required to simulate the responses of these materials accurately.

This paper uses an extension of the Creep-SCLAY1 model by Sivasithamparam et al. [19]. The Creep-SCLAY1S model adds the effect of structure to Creep-SCLAY1 that already takes into account anisotropy and creep. The model accounts for structure in the same way as the S-CLAY1S model developed by Karstunen et al. [8] based on the formulation proposed by Gens and Nova [4]. Existing models developed by e.g. Yin et al. [28] and Grimstad et al. [5] already take into account these three different features. The model has some major similarities with Yin et al.[28] and Grimstad et al. [5] models, as well as differences. In order to avoid any confusion in different definitions of some model parameters and key equations, the name of Creep-SCLAY1S is used to refer to the model in the format as introduced in Sivasithamparam et al. [19] with addition of bonding and destructuration. The advantage of Creep-SCLAY1, and therefore Creep-SCLAY1S, similarly to Leoni et al. [11] and Yin et al. [28] models over [5], is the use of the modified creep index parameter, which is directly related to the secondary compression coefficient $C_\alpha$ commonly used internationally.

The main drawback for the use of these types of advanced constitutive models is the number of parameters required. The Creep-SCLAY1S model requires in total 14 parameters, of which most can be directly derived from experimental data. Nevertheless, some are not directly measurable, such as some parameters used to describe the evolution of anisotropy and structure (material degradation). These parameters are estimated through indirect methods, such as calibration of the model response against the soil response measured in non-standard laboratory tests or optimisation methods [3, 12, 15, 16, 20, 25, 27]. For optimisation methods, however, it is of paramount importance to know the bounds for the values of these parameters prior to calibration. In this paper, a method to estimate these bounds is proposed for the three most important parameters for calibration: two related to structure and one related to anisotropy. In addition, the parameter relating Lode angle dependency is discussed. The current work will not only benefit the Creep-SCLAY1S model presented here, but the principles can be applied to a wide range of models that include formulations for structure and anisotropy, such as [2, 5, 6, 8, 11, 13, 19, 22, 24, 28]. The validity of the range proposed will be compared against the parameter values found in studies.

2 Description of the Creep-SCLAY1S model

Creep-SCLAY1S is an advanced soft soil model that accounts for creep, anisotropy and degradation of bonding. For simplicity, the model is presented in the triaxial stress space, which can be used only to model the response of cross-anisotropic samples subject to oedometric or triaxial loading paths [19]. For this case, the mean effective stress $p^{\prime }$ is defined by $p^{\prime } = \left( \sigma ^{\prime }_{a} + 2\sigma ^{\prime }_{r}\right) /3$ and the deviator stress q is defined by $q = \left( \sigma ^{\prime }_{a} - \sigma ^{\prime }_{r}\right)$. The volumetric strain rate $\dot{\varepsilon }_{v}$ and deviatoric strain rate $\dot{\varepsilon }_{q}$ are, respectively, defined by $\dot{\varepsilon }_{v} = \left( \dot{\varepsilon }_{a} + 2 \dot{\varepsilon }_{r}\right)$ and $\dot{\varepsilon }_{q} = 2/3\left( \dot{\varepsilon }_{a} - \dot{\varepsilon }_{r}\right)$. Subscripts a and r denote axial and radial directions. In the following, the compression is assumed positive. Analogously to classical elasto-plasticity, the total strain rate is expressed by:

$$\begin{aligned} \begin{aligned} \dot{\varepsilon }_{v} = \dot{\varepsilon }_{v}^{e} + \dot{\varepsilon }_{v}^{c}\\ \dot{\varepsilon }_{q} = \dot{\varepsilon }_{q}^{e} + \dot{\varepsilon }_{q}^{c} \end{aligned} \end{aligned}$$

(1)

$\dot{\varepsilon }_{v}^{c}$ and $\dot{\varepsilon }_{q}^{c}$ are the creep components of strain rates and $\dot{\varepsilon }_{v}^{e}$, and $\dot{\varepsilon }_{q}^{e}$ are the elastic components of strain rates.

The model assumes isotropic elastic behaviour similar to the modified Cam–Clay model [17]. The elastic volumetric strain rate $\dot{\varepsilon }_{v}^{e}$ and the elastic deviatoric strain rate $\dot{\varepsilon }_{q}^{e}$ are defined by:

$$\begin{aligned} \begin{aligned} \dot{\varepsilon }_{v}^{e} = \frac{\dot{p^{\prime }}}{K}\\ \dot{\varepsilon }_{q}^{e} = \frac{\dot{q}}{3G} \end{aligned} \end{aligned}$$

(2)

where the elastic bulk modulus $K = p^{\prime } / \kappa ^{*}$ and the elastic shear modulus $G = 3K \left( 1 - 2\nu ^{\prime }\right) / 2\left( 1+\nu ^{\prime }\right)$ are stress dependent. $\nu ^{\prime }$ is the Poisson’s ratio and $\kappa ^{*}$ is the modified swelling index defined as the slope of the initial part of the stress–strain curve in the $\varepsilon _{v}-\ln p^{\prime }$ plane (Fig. 1). It is assumed that there is no purely elastic domain: hence, there are always plastic (creep) deformations during the process due to the particular nature of the material.

Fig. 1

Definition of $\lambda ^{*}$, $\lambda ^{*}_{i}$ and $\kappa ^{*}$ from experimental data

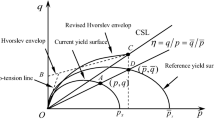
Three surfaces are used for the description of the state of the soil (Fig. 2). The first surface is called the normal consolidation surface (NCS) and delimits small and large creep strains (analogous to a bounding surface). The intersection of the vertical tangent to the ellipse with the $p^{\prime }$ axis is the isotropic preconsolidation pressure $p^{\prime }_{m}$. An other ellipse called the current stress surface (CSS) represents the current state of effective stresses. The intersection of the vertical tangent to the CSS with the horizontal axis is called the equivalent mean stress $p^{\prime }_{eq}$. $p^{\prime }_{eq}$ and $p^{\prime }_{m}$ define, respectively, the size of CSS and NCS. The effect of bonding is introduced by an imaginary intrinsic compression surface (ICS) proposed by Gens and Nova [4] to represent an unbonded soil with the same void ratio and fabric (see Fig. 2). This surface is hence assumed to be of the same shape and orientation as the NCS, but only smaller in size. The difference in size between the NCS and the ICS is related to the current amount of bonding $\chi$ by:

$$\begin{aligned} p^{\prime }_{m} = p^{\prime }_{mi}\left( 1+\chi \right) \end{aligned}$$

(3)

where $p^{\prime }_{mi}$ is the intrinsic isotropic preconsolidation pressure defining the size of the ICS. These three surfaces have the same shape and orientation, and are defined by the following Eq. [19]:

$$\begin{aligned} p^{\prime }_\mathrm{size} = p^{\prime } + \frac{\left( q-\alpha p^{\prime }\right) ^{2}}{\left( M^{2}\left( \theta _{\alpha } \right) - \alpha ^{2}\right) p^{\prime }} \end{aligned}$$

(4)

where $p^{\prime }_\mathrm{size}$ is equal to $p^{\prime }_{mi}$, $p^{\prime }_{eq}$ or $p^{\prime }_{m}$, respectively, to define the ICS, the CSS or the NCS. $\alpha$ is a scalar quantity used to describe the orientation of the surface and $M\left( \theta _{\alpha }\right)$ is the modified Lode angle formulation of the stress ratio at critical state. The Lode angle formulation is used to control the critical state stress ratio in triaxial extension ($M_{e}$) and in triaxial compression ($M_{c}$). $M\left( \theta _{\alpha }\right)$ is defined by Sheng et al. [18]:

$$\begin{aligned} M\left( \theta _{\alpha }\right) = M_{c}\left( \frac{2m^4}{1+m^4+\left( 1-m^4\right) \sin 3\theta _{\alpha }}\right) ^\frac{1}{4} \end{aligned}$$

(5)

where $m = M_{e} / M_{c}$. $\theta _{\alpha }$ is the modified Lode angle that depends on the stress state of the $\alpha$ line as follows:

$$\begin{aligned} \sin 3 \theta _{\alpha } = -\frac{3\sqrt{3}}{2} \frac{J_{3\alpha }}{J_{2\alpha }^{\frac{3}{2}}} \end{aligned}$$

(6)

where $J_{2\alpha }$ and $J_{3\alpha }$ are, respectively, the second and third invariant of the modified deviatoric stress tensor. These definitions are explicitly defined in Sivasithamparam et al. [19]. It should be noted that the value of m should be greater than 0.6 to preserve a physically realistic convex failure surface as shown in Fig. 3. Similar limitation is applicable for other models which adopt similar Lode angle-dependent formulation [14, 28, 29]. The value of $m = 1$ results in a circular Drucker–Prager failure surface.

Fig. 2

Current State Surface (CSS) and normal consolidation surface (NCS) of the Creep-SCLAY1S model and the direction of viscoplastic strains

Fig. 3

Failure surfaces in the deviatoric plane

The Creep-SCLAY1S model assumes an associated flow rule. This is a reasonable assumption for natural clays when using a model that accounts for evolution of anisotropy [7, 23]. Therefore, the creep strain rates are defined as:

$$\begin{aligned} \dot{\varepsilon }_{v}^{c} = \dot{\wedge }\frac{\partial p^{\prime }_{eq} }{ \partial p^{\prime }}\,\, \hbox{and} \,\,\dot{\varepsilon }_{q}^{c} = \dot{\wedge }\frac{\partial p^{\prime }_{eq} }{ \partial q} \end{aligned}$$

(7)

$\dot{\wedge }$ is the viscoplastic multiplier proposed by Sivasithamparam et al. [19]:

$$\begin{aligned} \dot{\wedge } = \frac{\mu _{i}^{*}}{\tau }\left( \frac{p^{\prime }_{eq}}{p^{\prime }_{m}}\right) ^{\beta } \left( \frac{M_{c}^{2} - \alpha _{K_{0}^{nc}}^2}{M_{c}^{2} - \eta _{K_{0}^{nc}}^2}\right) \end{aligned}$$

(8)

$\mu _{i}^{*}$ is the modified intrinsic creep index measured in the $\varepsilon _{v} - \ln t$ plane. It is an intrinsic material property, i.e. it should be derived from data where all bonding is erased (either at sufficiently large values of stress so that any bonding is erased or tests on reconstituted soil samples). $\mu _{i}^{*}$ is the limit value of the slope of the curve in the $\varepsilon _{v} - \ln t$ when t is increasing (see Fig. 4). The value of $\mu _{i}^{*}$ should be derived using the same unit time as of the reference time $\tau$. In these materials, the size of the NCS depends on the loading rate. The reference time $\tau$ relates to the duration of the load step in 1D compression test used to obtain the initial preconsolidation pressure (1D yield stress). For example, if the initial apparent preconsolidation pressure is derived from a standard 24 h oedometer test, the reference time $\tau$ is set to 24 h [11]. $\beta$ is defined as:

$$\begin{aligned} \beta = \frac{\lambda _{i}^{*}-\kappa ^{*}}{\mu _{i}^{*}} \end{aligned}$$

(9)

where $\lambda ^{*}_{i}$, the modified intrinsic compression index, is the slope of the intrinsic compression line in $\varepsilon _{v}-\ln p^{\prime }$ plane (see Fig. 1). $\alpha _{K_{0}^{nc}}$ is the inclination of the ICS, CSS and NCS corresponding to that produced by an 1D consolidation in normally consolidated state. The right term of Eq. 8 is added to ensure that under oedometer conditions, the model corresponds to the classical relation [21]:

$$\begin{aligned} \dot{\varepsilon }_{v}^{c} = \frac{\mu _{i}^{*}}{\tau }\left( \frac{p^{\prime }_{eq}}{p^{\prime }_{m}}\right) ^{\beta } \end{aligned}$$

(10)

Fig. 4

Definition of $\mu ^{*}$, for high value of stress or for reconstituted sample, when all the structure is erased, $\mu ^{*} = \mu _{i}^{*}$

The Creep-SCLAY1S model takes into account three hardening processes: isotropic hardening and structural hardening which will affect the size of ICS and NCS, and rotational hardening which will affect the orientation of the three surfaces. The isotropic hardening rule relates the change of the intrinsic isotropic preconsolidation pressure $p^{\prime }_{mi}$ with volumetric creep strains rate $\dot{\varepsilon }^{c}_{v}$ as follows:

$$\begin{aligned} \dot{p}'_{mi} = \frac{p^{\prime }_{mi}}{\lambda _{i}^{*}-\kappa ^{*}}\dot{\varepsilon }_{v}^{c} \end{aligned}$$

(11)

The second hardening law is the rotational hardening rule, which relates the evolution of anisotropy to creep strain rates by Sivasithamparam et al. [19]:

$$\begin{aligned} \dot{\alpha } = \omega \left[ \left( \frac{3q}{4p^{\prime }}- \alpha \right) \left\langle \dot{\varepsilon }_{v}^{c}\right\rangle + \omega _{d} \left( \frac{q}{3p^{\prime }}-\alpha \right) \left| \dot{\varepsilon }_{q}^{c}\right| \right] \end{aligned}$$

(12)

$\left\langle . \right\rangle$ are the Macaulay brackets which means that $\left\langle \dot{\varepsilon }_{v}^{c} \right\rangle = 0$ if $\dot{\varepsilon }_{v}^{c} < 0$ and $\left\langle \dot{\varepsilon }_{v}^{c} \right\rangle = \dot{\varepsilon }_{v}^{c}$ if $\dot{\varepsilon }_{v}^{c}\ge 0$. The modulus sign is needed due to the sign convention typically used in triaxial testing. Equation 12 relates the evolution of the anisotropy to volumetric creep strain rate $\dot{\varepsilon }_{v}^{c}$ and deviatoric creep strain rate $\dot{\varepsilon }_{q}^{c}$. The evolution of $\alpha$ causes a rotation of the normal consolidation surface (NCS), the intrinsic compression surface (ICS) and the current stress surface (CSS). $\omega$ is the absolute effectiveness of rotational hardening, and $\omega _{d}$ is the relative effectiveness of deviatoric creep strain rate $\dot{\varepsilon }_{q}^{c}$ and volumetric creep strain rate $\dot{\varepsilon }_{v}^{c}$ in the rotational hardening. At the microstructural level, these two parameters are related to the rate of rotation of the particles and particle contact, i.e. changes in fabric anisotropy, of the soil due to the creep strain rate.

The third hardening law relates the degradation of bonding with creep strains. The evolution of structure, characterised by the debonding rate $\dot{\chi }$ as a function of the volumetric creep strain rate $\dot{\varepsilon }_{v}^{c}$ and deviatoric creep strain rate $\dot{\varepsilon }_{q}^{c}$, is expressed by:

$$\begin{aligned} \dot{\chi } = -a \chi \left( \left| \dot{\varepsilon }_{v}^{c}\right| + b\left| \dot{\varepsilon }_{q}^{c}\right| \right) \end{aligned}$$

(13)

where the absolute rate of destructuration a, and the relative rate of destructuration b, are parameters controlling the rate of destructuration of the soil. At the microstructural level, these two parameters are controlling the rate of breakage of the bonds between particles/aggregates due to the creep strain rate. No chemical debonding is assumed in this model.

The initial size of the CSS ($p^{\prime }_{eq0}$) is derived from the in situ axial effective stress $\sigma ^{\prime }_{0a}$, assuming value of in situ $K_{0}$ (ratio between in situ radial and axial stresses) and of $\alpha _{0}$ ($\alpha _{0}$ is the initial inclination of the surfaces). The initial size of the NCS is subsequently derived from the in situ vertical effective stress $\sigma ^{\prime }_{0a}$, the assumed values of $K_{0}^{nc}$ (ratio between radial and axial stresses in a normally consolidated state) and $\alpha _{0}$, and the value of the pre-overburden pressure POP or over-consolidation ratio OCR. POP is defined by :

$$\begin{aligned} POP = \sigma _{p0} - \sigma ^{\prime }_{0a} \end{aligned}$$

(14)

where $\sigma _{p0}$ is the apparent vertical preconsolidation pressure. OCR is defined by:

$$\begin{aligned} OCR = \frac{\sigma _{p0}}{\sigma ^{\prime }_{0a}} \end{aligned}$$

(15)

The Creep-SCLAY1S model requires 14 parameters divided into 11 soil constants:

• the modified swelling index $\kappa ^{*}$,

• the Poisson’s ratio $\nu ^{\prime }$,

• the modified intrinsic compression index $\lambda _{i}^{*}$,

• the slope of critical state line in compression $M_{c}$,

• the slope of critical state line in extension $M_{e}$,

• the intrinsic modified creep index $\mu _{i}^{*}$,

• the reference time $\tau$,

• the absolute effectiveness of rotational hardening $\omega$,

• the relative effectiveness of rotational hardening $\omega _{d}$,

• the absolute rate of destructuration a,

• the relative rate of destructuration b,

and 3 initial state variables:

• the pre-overburden pressure POP or the over-consolidation ratio OCR,

• the initial inclination of the ICS, CSS and NCS $\alpha _{0}$,

• the initial amount of bonding $\chi _0$.

The value of the initial void ratio $e_0$ is also useful if comparison within the void ratio versus effective stress plane against experimental data are made. The value of the initial void ratio has no influence on the strain–stress relation. For simplicity, in the following, we use symbol $\xi ^{*}_{i}$ equal to $\lambda _{i}^{*}-\kappa ^{*}$.

3 Bounds for parameters related to structure

In order to take into account the apparent bonding, Creep-SCLAY1S uses three parameters: the initial amount of bonding $\chi _0$, the relative rate of destructuration b and the absolute rate of destructuration a. The initial amount of bonding $\chi _0$ is generally related to the experimentally obtained soil sensitivity, which is a simple routine test. Parameters a and b, however, cannot be measured directly and hence require an optimisation procedure. Some specialist tests (i.e. drained consolidation at two constant stress paths, one with high stress ratio and one with almost zero/negative stress ratio, see Koskinen et al. [10] and Karstunen et al. [8] for details) may be used to increase the accuracy of the calibration process, but these tests are normally not available. To perform such optimisation procedure, appropriate range for the values for a and b is required. In soft clays a reasonable assumption is that the deviatoric creep strains have less or equal influence as the volumetric creep strains on the destructuration process, giving b bounds $0<b<1$. Usually, a is unknown before model calibration against experimental results. In the following, a method is proposed to get a range of values for the future calibration of a.

Isotropic hardening and destructuration hardening have comparable effects in the sense that they lead to either an increase or a decrease in the size of the normal consolidation surface (NCS). Differentiation of Eq. 3 gives:

$$\begin{aligned} \dot{p}'_{m} = \dot{p}'_{mi} + \dot{\chi }p^{\prime }_{mi} + \chi \dot{p}'_{mi} \end{aligned}$$

(16)

By combining Eqs. 3, 11 and 16, the hardening rule for size becomes:

$$\begin{aligned} \frac{\dot{p}'_{m}}{p^{\prime }_{m}} = \frac{1}{\xi ^{*}_{i}}\dot{\varepsilon }_{v}^{c} + \frac{\dot{\chi }}{1 + \chi } \end{aligned}$$

(17)

In this equation, the effect of structure hardening and isotropic hardening on the evolution of the preconsolidation pressure is obtained. Integrating Eq. 17 leads to:

$$\begin{aligned} \ln r_{p_m} = \frac{1}{\xi ^{*}_{i}}\Delta \varepsilon _{v}^{c} + \ln \frac{1+\frac{\chi _0}{r_{\chi }}}{1+\chi _0} \end{aligned}$$

(18)

where $\Delta \varepsilon _{v}^{c}$ and $r_{\chi } = \chi _0 / \chi _1$ are, respectively, the increment in volumetric strain and the ratio between the initial amount of bonding $\chi _0$ and the final amount of bonding $\chi _1$ corresponding to a load path that increases the preconsolidation pressure from $p_{m0}$ to $p_{m1} = r_{p_{m}}p_{m0}$.

3.1 Upper bound for a

Combining Eqs. 13 and 17 results in:

$$\begin{aligned} \frac{\dot{p}'_{m}}{p^{\prime }_{m}} = \frac{1}{\xi ^{*}_{i}}\dot{\varepsilon }_{v}^{c}-\frac{a\chi }{1+\chi }\left| \dot{\varepsilon }_{v}^{c}\right| - \frac{ab\chi }{1+\chi }\left| \dot{\varepsilon }_{q}^{c}\right| \end{aligned}$$

(19)

It can be assumed that for most clays under isotropic loading, the isotropic preconsolidation pressure always increases. In Eq. 19, $\dot{p}'_{m}/ p^{\prime }_{m} \ge 0$ implies that

$$\begin{aligned} a \le \frac{1+\chi }{\chi \xi ^{*}_{i} \left( 1+b\frac{\left| \dot{\varepsilon }_{q}^{c}\right| }{\dot{\varepsilon }_{v}^{c}}\right) } \end{aligned}$$

(20)

for the entire test. During isotropic compression, ($q=0$) equations 4 and 7 reduce to:

$$\begin{aligned} \frac{\dot{\varepsilon }_{q}^{c}}{\dot{\varepsilon }_{v}^{c}} = -\frac{2\alpha }{M\left( \theta \right) ^{2}} \end{aligned}$$

(21)

When compressing isotropically a natural material, with an in situ normally consolidated history, $M\left( \theta \right) = M_{e}$ because isotropic stress path is below the $\alpha -line$ [23]. $M_{e}$ could be measured, or assumed based on Mohr–Coulomb failure criteria. Moreover, for an initial fabric resulting from a normally consolidated history in the ground, during subsequent isotropic compression $\dot{\varepsilon }_{v}^{c}$ is positive and $\dot{\varepsilon }_{q}^{c}$ is negative according to the model. As a result:

$$\begin{aligned} \frac{\left| \dot{\varepsilon }_{q}^{c}\right| }{\dot{\varepsilon }_{v}^{c}} = \frac{2\alpha }{M_{e}^{2}} \end{aligned}$$

(22)

Equation 20 then becomes:

$$\begin{aligned} a \le \frac{1+\chi }{\chi \xi ^{*}_{i} \left( 1+2b\frac{\alpha }{M_{e}^{2}}\right) } \end{aligned}$$

(23)

As $\chi$ is decreasing during loading, the right term of the inequality increases until infinity when $\chi$ tends to zero. That means that for any value of a, when erasing the structure, the isotropic effect will start to surpass the bond degradation effect. The lowest value of the right term occurs for the biggest value of $\chi$: the initial value $\chi _0$. The lowest value of the right term occurs for the biggest value of $\alpha / M_{e}^{2}$ which is for $\alpha = \alpha _{K_{0}^{nc}}$ as $\alpha$ will decrease during the isotropic loading. Then, in order to respect the inequality during the entire isotropic loading test:

$$\begin{aligned} a \le \frac{1+\chi _{0}}{\chi _{0} \xi ^{*}_{i} \left( 1+2b\frac{\alpha _{K_{0}^{nc}}}{M_{e}^{2}}\right) } \end{aligned}$$

(24)

Here, the initial amount of bonding does not have a strong influence on the upper bound values of a, as long as it is sufficiently large ($\chi _0 \ge 10$). On the contrary, the value of $\xi ^{*}_{i}$ has a strong influence on this upper bound value (see Fig. 5). Using typical values for soft clays ($\xi ^{*}_{i} = 0.1$, $\chi _{0} = 20$), $M_c = 1.2$ (which gives $\alpha _{K_{0}^{nc}} = 0.46$ from Eq. 30 and $M_e=0.9$) and $b=0.2$ (a typical value for various clay for which S-CLAY1S model has been calibrated so far [9]), an upper bound value of a equal to 8.6 is obtained.

Fig. 5

Evolution of the upper bound for a as a function of $\xi ^{*}_{i}$ for $\chi _0 = 20$, $\alpha _0 = 0.46$ and $M_e = 0.9$

In the case of an isotropic material ($\alpha _0=0$), or if $b=0$, inequality Eq. 24 becomes:

$$\begin{aligned} a \le \frac{1+\chi _{0}}{\chi _{0} \xi ^{*}_{i} } \end{aligned}$$

(25)

In that case, again using typical values for soft clays ($\xi ^{*}_{i}= 0.1$, $\chi _{0} = 20$), an upper bound value for a equal to 10.5 is derived. The advantage of this formulation is that there are less parameters to take into account, and as such it is a convenient first assessment. It, however, is an higher bound and could result in a situation where isotropic hardening has less effect than bond degradation at the beginning of the test, in the case of nonzero creep deviatoric strain rate. For high values of b, this upper bound could differ quite considerably from the previous formulation.

Fig. 6

Evolution of the upper bound and lower bound for a as a function of $\xi ^{*}_{i}$ for $\chi _0 = 20$, $\alpha _0 = 0.46$, $M_e = 0.9$, $b = 0.2$. In grey, range of possible values for a

3.2 Lower bound for a

An isotropic loading is considered for a soil which has an initial amount of bonding equal to $\chi _{0}$ and an initial preconsolidation pressure equal to $p^{\prime }_{m0}$. Integrating Eq. 13 results into:

$$\begin{aligned} a = \frac{1}{\left| \Delta \varepsilon _{v}^{c}\right| + b\left| \Delta \varepsilon _{d}^{c}\right| } \ln r_{\chi } \end{aligned}$$

(26)

with $r_{\chi } = \chi _{0} / \chi _{1}$ the ratio between the initial amount of bonding $\chi _{0}$ and the final amount of bonding $\chi _{1}$. $\left| \Delta \varepsilon _{v}^{c}\right|$ and $\left| \Delta \varepsilon _{q}^{c}\right|$ are, respectively, the creep volumetric and deviatoric strains corresponding to this change in bonding amount. $\left| \Delta \varepsilon _{q}^{c}\right| \le \left| \Delta \varepsilon _{v}^{c}\right|$ is assumed at the end of isotropic loading, which can be rewritten in:

$$\begin{aligned} a \ge \frac{1}{\left| \Delta \varepsilon _{v}^{c}\right| \left( 1+b\right) } \ln r_{\chi } \end{aligned}$$

(27)

From Eq. 18, $\Delta \varepsilon _{v}^{c}$ is assessed by:

$$\begin{aligned} \Delta \varepsilon _{v}^{c} = \left[ \ln \frac{r_{p_{m}}\left( 1+\chi _0\right) }{1+\frac{\chi _0}{r_{\chi }}}\right] \xi ^{*}_{i} \end{aligned}$$

(28)

In natural soft clays, it is assumed that $r_{\chi } = 2$ at the end of an isotropic compression loading to $r_{p_{m}} = 2$ corresponds to a very low rate of destructuration. Hence, from inequality Eqs. 27 and 28, a is bounded by:

$$\begin{aligned} a \ge \frac{\ln 2}{\left[ \ln \left( 2+2\chi _0\right) -\ln \left( 1 + \frac{\chi _0}{2}\right) \right] \left( 1+b\right) \xi ^{*}_{i}} \end{aligned}$$

(29)

For example, for $\xi ^{*}_{i} = 0.1$, $\chi _0 = 20$, $b=0.2$, a lower bound value for a is 4.3. If b is unknown, taking $b=1$ in the previous formula will lead to a lower bound for a. Experimental data on the evolution of structure with loading may be required to have a better idea of the ratio of bonding numbers $r_{\chi }$ for a certain ratio of preconsolidation pressure $r_{p_{m}}$. The range of possible values for a  as a function of $\xi ^{*}_{i}$ is plotted in Fig. 6.

4 Bounds for parameters related to anisotropy

In order to take into account anisotropy of the soil and its evolution, three parameters are needed: the initial inclination of ICS, CSS and NCS represented by $\alpha _{0}$, the relative effectiveness of creep strains in rotational hardening $\omega _{d}$ and the absolute effectiveness of rotational hardening $\omega$.

$\alpha _{0}$, the initial inclination of the ICS, CSS and NCS can be calculated assuming that the history of the soil deposit has been restricted to primarily one-dimensional straining to a normally consolidated or lightly overconsolidated state. In that case, the in situ inclination of the yield curve corresponds to that produced by an 1D ($K_{0}^{nc}$) consolidation to a normally consolidated state and could be expressed as follows [23]:

$$\begin{aligned} \alpha _0 = \alpha _{K_{0}^{nc}} = \frac{\eta _{K_{0}^{nc}}^{2}+3\eta _{K_{0}^{nc}}-M_{c}^{2}}{3} \end{aligned}$$

(30)

where $M_{c}$ is the slope of the critical state line in compression measured from drained or undrained triaxial compression tests. $\eta _{K_{0}^{nc}}$, the value of stress ratio corresponding to a normally consolidated value of $K_{0}^{nc}$, is assessed by $\eta _{K_{0}^{nc}} = 3\left( 1-K_{0}^{nc}\right) / \left( 1+2K_{0}^{nc}\right)$. $K_{0}^{nc} = 1-\sin \varphi ^{\prime }$ using Jaky’s formula and the internal friction angle $\varphi ^{\prime }$ is related to $M_{c}$ by $M_{c} = 6\sin \varphi ^{\prime } / \left( 3-\sin \varphi ^{\prime }\right)$. Theoretically, there is only one possible $\omega _{d}$ value expressed by Wheeler et al. [23]:

$$\begin{aligned} \omega _d = \frac{3\left( 4M_{c}^{2}-4\eta _{K_{0}^{nc}}^{2}-3\eta _{K_{0}^{nc}}\right) }{8\left( \eta _{K_{0}^{nc}}^{2}-M_{c}^{2}+2\eta _{K_{0}^{nc}}\right) } \end{aligned}$$

(31)

Typically, $\omega$ is a parameter that need to be calibrated against experimental data. In the following a method to get a range for the value of $\omega$ is proposed. For the assessment of $\omega$, an isotropic path is followed, which has the advantage of erasing the anisotropy. As previously, we can write in the case of isotropic compression:

$$\begin{aligned} \frac{\left| \dot{\varepsilon }_{q}^{c}\right| }{\dot{\varepsilon }_{v}^{c}} = \frac{2\alpha }{M_{e}^{2}} \end{aligned}$$

(32)

In the case of an isotropic compression loading, $q = 0$, the anisotropic hardening rule, equation (12), becomes:

$$\begin{aligned} \dot{\alpha } = - \alpha \omega \left( \dot{\varepsilon }_{v}^{c} + \omega _{d} \left| \dot{ \varepsilon }_{q}^{c}\right| \right) \end{aligned}$$

(33)

Combining Eqs. (32) and (33), leads to:

$$\begin{aligned} -\omega . \dot{\varepsilon }_{v}^{c} = \frac{ M_{e}^{2} \dot{\alpha } }{ M_{e}^{2} \alpha + 2 \omega \omega _{d} \alpha ^{2}} \end{aligned}$$

(34)

Integrating this equation results in an expression for $\omega$:

$$\begin{aligned} \omega = \frac{1}{\Delta \varepsilon _{v}^{c}} \ln \frac{r_{\alpha } + \frac{2\omega _{d}.\alpha _{0}}{M_{e}^{2}}}{1+ \frac{2\omega _{d}.\alpha _{0}}{M_{e}^{2}} } \end{aligned}$$

(35)

where $\Delta \varepsilon _{v}^{c}$ is the plastic volumetric stain increment and $r_{\alpha } = \alpha _0 / \alpha _1$ is the ratio between the initial orientation of the surfaces $\alpha _0 = \alpha _{K_{0}^{nc}}$ (in situ normally consolidated sample) and the orientation of the surface after the isotropic loading $\alpha _1$. In the formulation proposed by Leoni et al. [11] (Equation 32 of their paper) for the determination of $\omega$, a negative sign was present due to a sign error in the ratio between deviatoric and volumetric creep strain rates from the flow rule. The proposed formulation for $\omega$, Eq. 35, with a positive value avoids indetermined values for $\omega$, which was a problem in the previous formulation [19].

4.1 $\omega$ range for model without structure

First of all, a range for $\omega$ is assessed for models which do not account for structure, such as Creep-SCLAY1 or SCLAY1. In Creep-SCLAY1 or SCLAY1, the hardening rule in size is similar to the law in the modified Cam–Clay Model:

$$\begin{aligned} \dot{p}'_{m} = \frac{p^{\prime }_{m}}{\lambda ^{*}-\kappa ^{*}}\dot{\varepsilon }_{v}^{c} = \frac{p^{\prime }_{m}}{\xi ^{*}}\dot{\varepsilon }_{v}^{c} \end{aligned}$$

(36)

where $\lambda ^{*}$ is the slope of the post-yield compression line in $\varepsilon _{v}^{p}-\ln p^{\prime }$ (Fig. 1). $\xi ^{*}$ is equal to $\lambda ^{*}-\kappa ^{*}$ and is related to irrecoverable compression. Note that the Creep-SCLAY1S model becomes the Creep-SCLAY1 model if $\chi _{0}=0$ (which leads to $\dot{\chi } =0$) and if $\lambda ^{*}$ is used instead of $\lambda _{i}^{*}$.

Integrating Eq. (36) leads to:

$$\begin{aligned} \Delta \varepsilon _{v}^{c} = \xi ^{*} \ln r_{pm} \end{aligned}$$

(37)

where $\xi ^{*} = \lambda ^{*} - \kappa ^{*}$ and $\Delta \varepsilon _{v}^{c}$ is the increment of volumetric strain corresponding to an increase in preconsolidation pressure from the initial preconsolidation pressure of the soil $p^{\prime }_{m0}$ to $p^{\prime }_{m1} = r_{p_m} p^{\prime }_{m0}$. By considering an isotropic loading for a soil which has a preconsolidation pressure equal to $p^{\prime }_{m0}$ and an initial inclination of the surfaces equal to $\alpha _0 = \alpha _{K_0^{nc}}$, then combining Eqs. 35 and 37 results in:

$$\begin{aligned} \omega \xi ^{*} = \frac{1}{\ln r_{p_m} } \ln \frac{r_{\alpha } + \frac{2\omega _{d}\alpha _{0}}{M_{e}^{2}}}{1+ \frac{2\omega _{d}\alpha _{0}}{M_{e}^{2}} } \end{aligned}$$

(38)

From Eq. 38, $r_{\alpha }$ is expressed as:

$$\begin{aligned} r_{\alpha } = \left( 1+A\right) r_{p_{m}}^{\omega \xi ^{*}} - A \end{aligned}$$

(39)

where $A = 2\omega _{d}\alpha _{0} / M_{e}^{2}$ and $r_{\alpha }$ are both increasing functions of $M_c$. In that equation, it is worth to note that $\xi ^{*}$ has a similar effect as $\omega$ on the evolution of anisotropy. Indeed, when $\xi ^{*}$ increases, the increment of irrecoverable strains increases and then anisotropy decreases according to the rotational hardening rule (Eq. 12). In Kaolinite clay, Anandarajah et al. [1] conclude from experimental observation that most of the anisotropy is erased during a compressive isotropic loading till $r_{p_m} = 2$. On the other hand, Zentar et al. [30] suggest that anisotropy is erased during an isotropic loading when the stress level is about three times the preconsolidation pressure. By using these experimental results, it is possible to assess bounds for $\omega$ using Eqs. 38 and 39. As the assessment of $r_\alpha$ depends on A and therefore on $M_c$ ($\omega _{d}$, $\alpha _{0}$ and $M_{e}$ can be directly derived from the value of $M_c$), a value of $M_c=0.8$ is considered for the assessment of the upper bound whilst a value of $M_c=1.6$ is considered for the assessment of the lower bound (from the literature, $M_c$ is in the range of 0.8 and 1.6 in soft clays). From Eq. 38, considering a loss of anisotropy equal to $r_{\alpha } = 25$ at the end of an isotropic loading till $r_{p_m} =2$, $M_c =0.8$, $\omega$ is equal to:

$$\begin{aligned} \omega = \frac{2.9}{\xi ^{*} \ln 2} \approx \frac{4.2}{\xi ^{*}} \end{aligned}$$

(40)

From Eq. 38, considering a loss of anisotropy equal to $r_{\alpha } = 10$ at the end of an isotropic loading till $r_{p_m} =3$, $M_c = 1.6$, $\omega$ is equal to:

$$\begin{aligned} \omega = \frac{1.6}{\xi ^{*} \ln 3 } \approx \frac{1.5}{\xi ^{*}} \end{aligned}$$

(41)

These two particular values of $\omega$ are then used in Eq. 39 to assess the evolution of $r_{\alpha }$ as a function of $r_{p_m}$. For $\omega = 4.2 / \xi ^{*}$, it can be noted that $r_\alpha \approx 10$ for $r_{p_{m}} = 1.6$, which means that large part of the anisotropy is already erased for $r_{p_{m}}=1.6$, and $r_\alpha = 25$ for $r_{p_{m}} = 2$ (see Fig. 7). This results show that Eq. 40 defines a reasonable upper bound for $\omega$. For $\omega = 1.5 / \xi ^{*}$, it can be noted that $r_\alpha \approx 5$ for $r_{p_{m}} = 2$, which means that still some anisotropy is present for $r_{p_{m}} = 2$ (see Fig. 7). Hence, equation 41 defines a reasonable lower bound for $\omega$. Finally, the range for $\omega$ will be:

$$\begin{aligned} \frac{1.5}{\xi ^{*}} \le \omega \le \frac{4.2}{\xi ^{*}} \end{aligned}$$

(42)

It may be interesting to make an experimental investigation of the evolution of anisotropy during isotropic compression loading and compare value with Eq. 39 to have a better assessment of $\omega$. Unfortunately, not many results of experiments are yet available.

Fig. 7

Evolution of $r_{\alpha }$ as a function of $r_{pm}$ for different values of $\omega$. $M_c$ is equal to 1.6 for $\omega = 1.5 / \xi ^{*}$ and $M_c$ is equal to 0.8 for $\omega = 4.2 / \xi ^{*}$

4.2 $\omega$ range for models with bonding and bond degradation

In this section, we propose a range of values for $\omega$ for the Creep-SCLAY1S model and similar models. From the isotropic and destructuration hardening it follows that:

$$\begin{aligned} \Delta \varepsilon _{v}^{c} = \left[ \ln \frac{r_{pm}\left( 1+\chi _0\right) }{1+\frac{\chi _0}{r_{\chi }}}\right] \xi ^{*}_{i} \end{aligned}$$

(43)

$\Delta \varepsilon _{v}^{c}$ and $r_{\chi }$, are, respectively, the increment in volumetric creep strain and the ratio between the initial amount of bonding $\chi _0$ and the final amount of bonding corresponding to a load path that increases the preconsolidation pressure from the initial preconsolidation pressure $p_{m0}$ to $p_{m1} = r_{p_{m}}p_{m0}$. Keep in mind that in this equation $\xi ^{*}_{i}$ is used (which has a lower value than $\xi ^{*}$). By considering an isotropic loading for a soil which has a preconsolidation pressure equal to $p^{\prime }_{m0}$, an initial inclination of the surfaces equal to $\alpha _0 = \alpha _{K_0^{nc}}$ and an initial amount of bonding equal to $\chi _0$, and then combining Eqs. 35 and 43, yields:

$$\begin{aligned} \omega \xi ^{*}_{i}= \frac{1}{\ln \frac{r_{pm}\left( 1+\chi _0\right) }{1+\frac{\chi _0}{r_{\chi }}}} \ln \frac{r_{\alpha } + \frac{2\omega _{d}\alpha _{0}}{M_{e}^{2}}}{1+ \frac{2\omega _{d}\alpha _{0}}{M_{e}^{2}} } \end{aligned}$$

(44)

From Eq. 44, $r_{\alpha }$ is expressed as:

$$\begin{aligned} r_{\alpha } = \left( 1+A\right) \left[ r_{p_{m}}\frac{1+\chi _0}{1+\frac{\chi _0}{r_{\chi }}}\right] ^{\omega \xi ^{*}_{i}} - A \end{aligned}$$

(45)

where $A = 2\omega _{d}\alpha _{0} / M_{e}^{2}$. For a particular value of $r_{p_{m}}$, $r_{\alpha }$ is an increasing function of $\omega \xi ^{*}_{i}$, $\chi _{0}$ and $r_{\chi }$. Hence, the value of $r_{\alpha }$ will depend on the initial amount of bonding $\chi _{0}$ and on the rate of destructuration, and therefore, on parameters a and b. Destructuration and loss of anisotropy are hence coupled in Creep-SCLAY1S. When looking for an upper bound for $\omega$, as $r_{\alpha }$ is an increasing function of $\omega$ and $r_{\chi }$, a minimum rate of destructuration should be used in order to maximise $\omega$. As previously, in natural soft clays, it is assumed that $r_{\chi }$ equal to 2 at the end of an isotropic compression loading till $r_{p_{m}} = 2$ corresponds to a minimum rate of destructuration. For this particular case, it is assumed that $r_{\chi } \approx r_{p_{m}}$ during the entire isotropic loading from $r_{p_{m}}=1$ to $r_{p_{m}}=2$. Comparing this assumption with simulated isotropic loading resulting in $r_{\chi }$ equal to 2 for $r_{p_m} =2$, this approximation captures well the behaviour of the model (see Fig. 8).

Fig. 8

Evolution of $r_{\chi }$ as a function $r_{p_{m}}$ during isotropic loading from $r_{p_{m}}=1$ till $r_{p_{m}}=2$ for a final ratio of bonding equal to 2. Comparison between simulation results (with $\chi _0 = 34$) and $r_{\chi } = r_{p_{m}}$

From Eq. 44, considering, respectively, a loss of anisotropy equal to $r_{\alpha } = 25$ and a degradation of bonds equal to $r_{\chi }=2$ (minimum degradation rate) at the end of an isotropic loading till $r_{p_m} =2$, $M_c =0.8$, we get an upper bound for $\omega$ equal to:

$$\begin{aligned} \omega \le \frac{2.9}{\xi ^{*}_{i}\ln \frac{2\left( 1+\chi _{0}\right) }{1+\frac{\chi _{0}}{2}}} \end{aligned}$$

(46)

Notably, the initial amount of bonding $\chi _0$ has only a small influence on this upper bound as long as $\chi _0 \ge 10$. Using $r_{\chi }= r_{p_{m}}$ in Eq. 45 and an upper bound value of $\omega$ defined by Eq. 46, the evolution of $r_{\alpha }$ as a function of $r_{p_{m}}$ ($1 \le r_{p_{m}} \le 2$) is assessed (Fig. 9) for different values of $\chi _0$. Significantly, the value of $\chi _0$ has a negligible effect on the evolution of $r_{\alpha }$ as a function of $r_{p_{m}}$ (see Fig. 9). In Fig. 9, it can be noted that $r_\alpha \approx 10$ for $r_{p_{m}} = 1.6$, which means that large part of the anisotropy is already erased for $r_{p_{m}}=1.6$, and $r_\alpha = 25$ for $r_{p_{m}} = 2$. This upper bound corresponds well with the assumption that all the anisotropy is erased in an isotropic compression loading to $r_{p_{m}} = 2$.

Fig. 9

Evolution of $r_{\alpha }$ as a function of $r_{p_m}$ for upper bound values of $\omega$ defined by Eq. 46, $M_c$ is equal to 0.8. Several curves are plotted for different values of $\chi _0$ in the range 1 to 1000

According to Eq. 45, it is possible to have a quite big value for $r_\alpha$ corresponding to a low value of $\omega$ and high value of $r_{\chi }$ corresponding to a high rate of destructuration. Moreover, the maximum rate of destructuration is quite hard to define in terms of evolution of $r_{\chi }$ as a function of $r_{p_{m}}$. So in the case of structure, a lower bound equal to zero for $\omega \xi ^{*}_{i}$ is proposed by default. Consequently, for a soil with an initial amount of bonding equal to $\chi _{0}$, the bounds of $\omega$ are:

$$\begin{aligned} 0 < \omega \le \frac{2.9}{\xi ^{*}_{i}\ln \frac{2\left( 1+\chi _{0}\right) }{1+\frac{\chi _{0}}{2}}} \end{aligned}$$

(47)

5 Comparison of the new bounds with available data

The values of parameters commonly used in the literature will be compared with the range derived. Given the relatively recent formulation of Creep-SCLAY1S, data of existing models using comparable model formulations and parameters for structure and anisotropy evolution will be used. Data corresponding to $\omega$ for models that do not account for structure (see Table 1) are first compared, followed by data corresponding to $\omega$ for models which account for bonding and degradation of bonds (see Table 2). Finally, data corresponding to parameter a will be presented (see Table 3).

5.1 Bounds for $\omega$ for models without structure

S-CLAY1 and Creep-SCLAY1 use similar parameters to model the rotational hardening and the structure hardening. Zentar et al. [30] suggested an alternative empirical formula to estimate $\omega$ for the S-CLAY1 model:

$$\begin{aligned} \frac{10}{\lambda } \le \omega \le \frac{15}{\lambda } \end{aligned}$$

(48)

where $\lambda$ is defined in the $e - \ln p$ plane. $\lambda$ is related to $\lambda ^{*}$ by $\lambda ^{*} = \frac{\lambda }{1+e_{0}}$. In the experiments made by Zentar et al. [30], $e_{0} \approx 2.2$. By using $e_{0}\approx 2.2$ and neglecting $\kappa ^*$ (relatively small in comparison to $\lambda ^{*}$ ), Eq. 42 becomes:

$$\begin{aligned} \frac{4.8}{\lambda } \le \omega \le \frac{13.5}{\lambda } \end{aligned}$$

(49)

The range of values resulting from the analytical considerations are close to those which were found experimentally by parameter calibration. Table 1 compares the previously suggested values of parameter $\omega$ against the proposed range. With the exception of one case, all the values used previously fall within the range proposed. Even for that case, the difference between the value used and the upper bound for $\omega$ is not very big. However, it is possible that for loading paths involving a lot of rotation, a better fit with experimental data may be found using values in the range proposed.

Table 1 Comparison between $\omega$ values used in the literature and the range of values proposed; without structure

5.2 Bounds for $\omega$ for models with structure

The parameter $\omega$ in the presence of structure is commonly used in previous models, such as S-CLAY1S, models developed by Yin et al. [28] and Grimstad et al. [5]. Table 2 presents the comparison against the reported values in the literature. Clearly, the $\omega$ values used in the literature never surpass the upper bound proposed in this paper.

Table 2 Comparison between $\omega$ values used in the literature and the upper bound value proposed; with structure

5.3 Bounds for structure parameter a

The parameter a that controls the absolute rate of destructuration is compared in Table 3. Again good agreement with previously reported values is obtained. Two exceptions are observed. First of all, the value of a proposed by Yin et al. [28], equal to 13.5, is somewhat larger than the upper bound which is equal to 13.1. In this case, the difference is not so big and the consequences will be negligible. The value proposed by Yildiz et al. [26] equal to 8 is quite low compared to the proposed lower bound 12.9. However, Yildiz et al. [26] seems to have taken a dummy value of 8 for a regardless of the other properties of the soil layer due to the lack of appropriate data for calibration of the a parameter. That resulted in the very low value for a. In that case, the performance of the model may be well improved by taking a value within the proposed range.

Table 3 Comparison of the values for parameter a of the literature with the proposed range of values

6 Conclusions

An extended formulation of the Creep-SCLAY1 model is presented that includes effects of structure. Most of the parameters required are easy to evaluate from experimental data. The structure parameter a and anisotropy parameter $\omega$, however, need calibration with the type of tests that are not normally available. For the first time a fundamental approach to obtain a range for these parameters is presented. Although the equations in the paper have been derived for a particular model, the same principles can be adopted for any model that accounts for initial anisotropy and its evolution, and/or bonding and destructuration. The method is based on combining theoretical considerations with physically sound assumptions based on experimental observations.

A very good agreement is observed between the range proposed, and the reported values for these parameters after calibration. The range proposed for these two parameters will then be very useful for further optimisation of these parameters. The range for $\omega$ for models which do not account for structure is given by Eq. 42, whilst the range for $\omega$ for models which account for structure is given by Eq. 47. The lower bound value of a is given by Eq. 29, and finally the upper bound value for a is given by Eq. 24. For both parameters a and $\omega$, the range of values is strongly dependent on the compressibility parameter $\xi ^{*}$ (or $\xi ^{*}_{i}$ if bonding effect are considered). The compressibility parameter and rate of destructuration have a great influence on the evolution of anisotropy during isotropic loading. We highlight that a quite widely used formula to estimate $\omega$ in [11] has a sign error, and with a correct formula indeterminate values are avoided. Finally, the new formula in the case of a model with a Lode angle formulation of the critical state stress ratio is proposed in Eq. 35. Physical bounds for the m parameter in the Lode angle dependency formulation are proposed.