A two-warehouse EOQ model with interval-valued inventory cost and advance payment for deteriorating item under particle swarm optimization

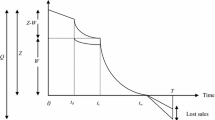
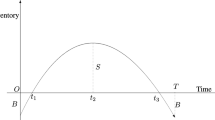
Abstract

Generally, most of the inventory costs are not always fixed due to uncertainty of competitive market. In the existing literature, it is found that several researchers have worked on uncertainty considering inventory parameters as fuzzy valued. In this work, we have represented the inventory parameters as interval. Using this concept, we have developed a two-warehouse inventory model with advanced payment, partial backlogged shortages. Due to uncertainty, this problem cannot be solved by existing direct/indirect optimization technique. For this purpose, different variants of particle swarm optimization techniques (viz. PSO-CO, WQPSO and GQPSO) have been developed to solve the problem of the proposed inventory model by using interval arithmetic and interval order relations. Finally, to illustrate and also to validate the proposed model, a numerical example has been solved and the best found solutions (which is either optimal solution or near optimal solution) obtained from different variants of PSO have been compared. Then, a sensitivity analysis has been performed to study the effect of changes of different parameters of the model on the optimal policy.

Appendices

Appendix A: Interval mathematics

An interval number is denoted by $A = \left[ {a_{L} ,a_{U} } \right]$ and defined by $A = \left[ {a_{L} ,a_{U} } \right] = \left\{ {x:a_{L} \le x \le a_{U} ,x \in R} \right\}.$, where $a_{L}$ and $a_{U}$ are lower and upper bounds, respectively. Any real number $x \in R$ can be expressed as an interval number [x, x] as degenerate with zero width. Also, interval number can be expressed in terms of centre and radius form as $A = \left[ {a_{c} ,a_{w} } \right] = \left\{ {x:a_{c} - a_{w} \le x \le a_{c} + a_{w} ,x \in R} \right\}$, where a_C = (a_L + a_U)/2 is the centre of the interval number and a_W = (a_U − a_L)/2, the radius of the interval number. The basic definitions of interval arithmetic are given Moore (Moore 1979) and which are given below:

Definition A.1

Let us consider A = [a_L, a_U] and B = [b_L, b_U] be any two interval numbers. Then, arithmetical operations such as addition, subtraction, multiplication of scalar number, multiplication and division of interval numbers are given below:

• 1. Addition:

  $$ A + B = \left[ {a_{L} ,a_{U} } \right] + \left[ {b_{L} ,b_{U} } \right] = \left[ {a_{L} + b_{L} ,a_{U} + b_{U} } \right]. $$

• 2. Subtraction:

  $$ A - B = \left[ {a_{L} ,a_{U} } \right] - \left[ {b_{L} ,b_{U} } \right] = \left[ {a_{L} ,a_{U} } \right] + \left[ { - b_{U} , - b_{L} } \right] = \left[ {a_{L} {-}b_{U} ,a_{U} - b_{L} } \right]. $$

• 3. Scalar multiplication:

  $$ \lambda A = \lambda \left[ {a_{L} , \, a_{U} } \right] = \left\{ \begin{aligned} &\left[ {\lambda a_{L} , \, \lambda a_{U} } \right] \quad {\rm if} \, \lambda \ge 0 \hfill \\ &\left[ {\lambda a_{U} , \, \lambda a_{L} } \right] \quad {\rm if} \, \lambda < 0, \hfill \\ \end{aligned} \right.\quad {\text{for}}\;{\text{any}}\;{\text{real}}\;{\text{number}}\;{\mathbb{R}}. $$

• 4. Multiplication:

  $$ A \times B = \left[ {\hbox{min} \left( {a_{L} b_{L} ,a_{L} b_{U} ,a_{U} b_{L} ,a_{U} b_{U} } \right),\hbox{max} \left( {a_{L} b_{L} ,a_{L} b_{U} ,a_{U} b_{L} ,a_{U} b_{U} } \right)} \right] $$

  Specially, $A \times B = [a_{L} b_{L} ,a_{U} b_{U} ]{\text{ for }}a_{L} ,b_{L} \ge 0$

• 5. Division:

  $$ \frac{A}{B} = A \times \left( {\frac{1}{B}} \right) = \left[ {a_{L} , \, a_{U} } \right] \times \left[ {\frac{1}{{b_{U} }}, \, \frac{1}{{b_{L} }}} \right],\quad {\text{provided}}\;0 \in \left[ {b_{L} ,b_{U} } \right] $$

Definition A.2

Integral power of an interval According to Hansen and Walster (2004), the definition of positive integral power of an interval $A = [a_{L} ,a_{U} ]$ is given by

$$ A^{n} = \left\{ {\begin{array}{*{20}l} {[1,1]} \hfill & {{\text{if }}n = 0} \hfill \\ {\left[ {a_{L}^{n} ,a_{U}^{n} } \right]} \hfill & {{\text{if }}a_{L}^{n} \le 0{\text{ or if }}n{\text{ is odd}}} \hfill \\ {\left[ {a_{U}^{n} ,a_{L}^{n} } \right]} \hfill & {{\text{if }}a_{U} \ge 0{\text{ and }}n{\text{ is even}}} \hfill \\ {\left[ {0,\hbox{max} \{ a_{L}^{n} ,a_{U}^{n} \} } \right]} \hfill & {{\text{if }}a_{L} \le 0 \le a_{U} {\text{ and }}n > 0{\text{ is even}}} \hfill \\ \end{array} } \right. $$

Definition A.3

$n$-th root of an interval According to Karmakar et al. (2009), the $n$-th root of an interval $A = [a_{L} ,a_{U} ]$ is given by

$$ \begin{aligned} A^{{\frac{1}{n}}} & = [a_{L} ,a_{U} ]^{{\frac{1}{n}}} = \sqrt[n]{{[a_{L} ,a_{U} ]}} \\ & = \left\{ {\begin{array}{*{20}l} {\left[ {\sqrt[n]{{a_{L} }},\sqrt[n]{{a_{U} }}} \right]} \hfill & {{\text{if }}a_{L} \ge 0{\text{ or if }}n{\text{ is odd}}} \hfill \\ {\left[ {0,\sqrt[n]{{a_{U} }}} \right]} \hfill & {{\text{if }}a_{L} \le 0,a_{U} \ge 0{\text{ and }}n{\text{ is even}}} \hfill \\ \phi \hfill & {{\text{if }}a_{U} < 0{\text{ and }}n{\text{ is even}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

where $\phi$ being the empty interval.

1.1 Order relations of interval numbers

Let us consider two interval numbers $A = [a_{L} ,a_{U} ]$ and $B = [b_{L} ,b_{U} ]$. Then, these two intervals may follow any one of the following three types:

• Type-1: Two intervals are disjoint, i.e. either $a_{L} < a_{U} \le b_{L} < b_{U}$ or $b_{L} < b_{U} \le a_{L} < a_{U}$

• Type-2: Two intervals are partially overlapping, i.e. either $a_{L} \le b_{L} \le a_{U} \le b_{U}$ or $b_{L} \le a_{L} \le b_{U} \le a_{U}$

• Type-3: One of the intervals contains the other one, i.e. either $a_{L} \le b_{L} < b_{U} \le a_{U}$ or $b_{L} \le a_{L} < a_{U} \le b_{U}$

The definitions of interval order relations between two interval numbers have been proposed by several researchers. Recently, Bhunia and Samanta (2014) modified the drawbacks of existing definitions and proposed the modified definitions. The definitions of Bhunia and Samanta (2014) are as follows:

Definition A.4

The interval order relation $\ge^{\hbox{max} }$ between two intervals $A = [a_{L} ,a_{U} ] = \left\langle {a_{c} ,a_{w} } \right\rangle$ and $B = [b_{L} ,b_{U} ] = \left\langle {b_{c} ,b_{w} } \right\rangle$, for maximization problems is as follows:

$$ A \ge^{max} B \Leftrightarrow \left\{ {\begin{array}{ll} {a_{c} > b_{c} \quad {\text{ if }}a_{c} \ne b_{c} } \\ {a_{w} \le b_{w} \quad {\text{ if }}a_{c} = b_{c} } \\ \end{array} } \right. $$

and $A >^{\hbox{max} } B \Leftrightarrow A \ge^{\hbox{max} } B{\text{ and }}A \ne B$.

Definition A.5

The interval order relation $\le^{\hbox{min} }$ between two intervals $A = [a_{L} ,a_{U} ] = \left\langle {a_{c} ,a_{w} } \right\rangle$ and $B = [b_{L} ,b_{U} ] = \left\langle {b_{c} ,b_{w} } \right\rangle$, for minimization problems is as follows:

$$ A \le^{\hbox{min} } B \Leftrightarrow \left\{ {\begin{array}{ll} {a_{c} < b_{c}\quad {\text{ if }}a_{c} \ne b_{c} } \\ {a_{w} \le b_{w} \quad {\text{ if }}a_{c} = b_{c} } \\ \end{array} } \right. $$

and $A <^{\hbox{min} } B \Leftrightarrow A \le^{\hbox{min} } B{\text{ and }}A \ne B$.

1.2 Mean, standard deviation and coefficient of variation of Interval Numbers

According to the Bhunia and Samanta (2014), the mean, variance, standard deviation and coefficient of variation of n interval numbers can be defined as follows:

Let $x_{i} = [x_{iL} ,x_{iU} ]$, $i = 1,2, \ldots ,n$, be the i-th observation of an interval number. Then, mean $(\bar{x})$ and standard deviation $\left( {\sigma_{x} } \right)$ of the intervals $x_{1} ,x_{2} , \ldots ,x_{n}$ are given as follows:

$$ \bar{x} = [\bar{x}_{L} ,\bar{x}_{U} ] = \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {x_{iL} } ,\frac{1}{n}\sum\limits_{i = 1}^{n} {x_{iU} } } \right], $$

and

$$ \sigma_{x} = [\sigma_{L} ,\sigma_{U} ] = \sqrt {\text{Var(x)}} = \left\{ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {[x_{iL} - \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{iU} } ,x_{iU} - \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{iL} ]} } \right)^{2} } } \right\}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$

Coefficient of variation (C.O.V.) of the interval numbers $x_{1} ,x_{2} , \ldots ,x_{n}$ is given as follows:

$$ C.O.V. = \frac{{\sigma_{x} }}{{\bar{x}}} \times 100 = \left[ {\frac{{\sigma_{L} }}{{\bar{x}_{U} }} \times 100,\frac{{\sigma_{U} }}{{\bar{x}_{L} }} \times 100} \right]. $$

Appendix B: Particle swarm optimization (PSO)

In PSO, the following notations have been used:

p_size	the population size or swarm size
m_gen	the maximum number of generation
χ	the constriction factor
c1( > 0)	the cognitive learning rate
c2( > 0)	the social learning rate
r1, r2	the uniformly distributed random numbers lying in the interval [0, 1].
v ( k) i	the velocity of i-th particle at k-th generation/iteration
x ( k) i	the position of i-th particle of population at k-th generation
p ( k) i	the best previous position of i-th particle at k-th generation
p ( k) g	the position of the best particle among all the particles in the population

PSO is a population-based derivative-free soft computing optimization technique based on the individual experience and social interaction. It is very useful and popular continuous optimization technique. In PSO, the potential solutions are called particles. These particles fly through the search space of the problem by following the current optimum particles. Generally, PSO begins with random particles positions (solutions) and then searches the optimum solutions from generation to generation in the search space. So, each particle is updated with two best positions (solutions) in the search space. The first one is called the best position (solution) and this best position is named by personal best position. It is denoted by $p_{i}^{(k)}$. The second one is called the current best position (solution). It is found so far by any particle in the population. This best value is called as global best and denoted by $p_{g}^{(k)}$.

In generation to generation, the velocity and position of i-th $\left( {i = 1,2, \ldots ,p\_{\text{size}}} \right)$ particle are updated in the following way:

$$ v_{i}^{(k + 1)} = wv_{i}^{(k)} + c_{1} r_{1} \left( {p_{i}^{(k)} - x_{i}^{(k)} } \right) + c_{2} r_{2} \left( {p_{g}^{(k)} - x_{i}^{(k)} } \right) $$

(B1)

and

$$ x_{i}^{(k + 1)} = x_{i}^{(k)} + v_{i}^{(k + 1)} $$

(B2)

where w is the inertia weight; $k\left( { = 1,2, \ldots ,m{\text{ - gen}}} \right)$ denotes the iteration (generation). The constants $c_{1} \left( { > 0} \right)$ and $c_{2} \left( { > 0} \right)$ are called the cognitive learning and social learning rates, respectively. These are the acceleration constants. These two constants have important role for varying the velocity of the particle converge to $p_{i}^{(k)}$ and $p_{g}^{(k)}$, respectively.

From Eq. (B1), it is observed that the updated rule of the velocity of i-th particle is followed by three factors: (1) past velocity of the particle, (2) the distance between the particle’s best past one and current one and (3) the distance between swarm’s best experience (the position of the best particle in the swarm) and the current position of the particle. The velocity of the particle in (B1) is also restricted by $\left[ { - v_{\hbox{max} } ,\,\,v_{\hbox{max} } } \right]$ where $v_{\hbox{max} }$ is called the maximum velocity. Selecting a too small value for $v_{\hbox{max} }$ causes very small updating of velocities and positions of particles in every iteration. Therefore, the algorithm may take a long time to converge and face the problem of be trapped at local minima. In order to overcome these situations, Clerc (1999), Clerc and Kennedy (2002) have developed improved velocity update rules simply considering a constriction factor $\chi$. According to them, the updated velocity is given by

$$ v_{i}^{(k + 1)} = \chi \left[ {v_{i}^{(k)} + c_{1} r_{1} \left( {p_{i}^{(k)} - x_{i}^{(k)} } \right) + c_{2} r_{2} \left( {p_{g}^{(k)} - x_{i}^{(k)} } \right)} \right] $$

(B3)

Here, the constriction factor $\chi$ is expressed as

$$ \chi = \frac{2}{{\left| {2 - \phi - \sqrt {\phi^{2} - 4\phi } } \right|}} $$

(B4)

where $\phi = c_{1} + c_{2} ,\,\,\phi > 4$ and $\chi$ is a function of $c_{1}$ and $c_{2}$. Usually, $c_{1}$ and $c_{2}$ are both set to be 2.05. Thus, $\phi$ is set to 4.1, and therefore, the constriction coefficient $\chi$ is 0.729. This PSO is also known as PSO-CO i.e. constriction coefficient-based PSO.

According to classical mechanics, position and velocity of the particle are determined by the trajectory of the particle which indicates that a particle moves along a determined trajectory along the search space. It is not true in quantum mechanics. In quantum mechanics, the position and velocity of a particle cannot be determined together, due to uncertainty principle. Trajectory of a particle is meaningless in quantum mechanics. According to quantum mechanics, if a particle has quantum nature in PSO, then PSO algorithm is bound to work in a different way. Using this nature, Sun et al. (2004a, b) have proposed a new concept in PSO algorithm which is known as quantum PSO (QPSO) and solved some problems. In their proposed PSO algorithm (QPSO), particles’ state equations are structured by wave function. The state of every particle is described by its local attracter p, and the mean optimal position (MP) is determined by the characteristic length L of $\delta$-trap. Here, MP enhances the cooperation between particles and particles’ waiting with each other; QPSO can prevent particles trapping into local minima. According to Sun et al. (2004a, b), the iterative equation for the position of the particle in QPSO is as follows:

$$ x_{ij}^{(k)} = \tilde{p}_{ij}^{(k)} \pm \beta^{\prime}\left| {m_{j}^{(k)} - x_{ij}^{(k)} } \right|\log \left( {\frac{1}{{u_{j} }}} \right) $$

(B.5)

where $u_{j}$ is a random number which uniformly distributed in (0, 1). The parameter $\beta^{\prime}$ is called the contraction–expansion coefficient. It controls the convergence rate of the QPSO algorithm which decreases linearly from 1.0 to 0.5. The global point is called mean best $m^{(k)}$ of the population at k-th iteration and is defined as the mean of the pbest positions of all particles. That is

$$ \begin{aligned} m^{(k)} & = \left( {m_{1}^{(k)} ,m_{2}^{(k)} , \ldots ,m_{n}^{(k)} } \right) \\ & = \left\{ {\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {p_{i1}^{(k)} } ,\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {p_{i2}^{(k)} } , \ldots ,\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {p_{in}^{(k)} } } \right\} \\ \end{aligned} $$

(B.6)

Taleizadeh et al. (2010) have solved a supply chain problem by using weighted PSO. Bhunia and Shaikh (2015) applied PSO-CO technique for solving a two-warehouse inventory problem with trade credit policy. Taleizadeh et al. (2017) have solved a multi-objective optimization problem by using meta-goal programming and firefly algorithm. Here, we have used PSC-CO, WQPSO and GQPSO for solving the interval-valued inventory problem with advance payment and partial backlogged shortage.

In WQPSO, the mean best position of QPSO is replaced by weighted mean best position and particles are ranked in increasing order (in case of minimization problem) according to their fitness values. Then, a weighted coefficient $\alpha_{i}$ is assigned linearly increasing with the particle’s rank. The mean best position $m^{(k)}$, therefore, is calculated as follows:

$$ \begin{aligned} m^{(k)} & = \left( {m_{1}^{(k)} ,m_{2}^{(k)} , \ldots ,m_{n}^{(k)} } \right) \\ & = \left\{ {\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {\alpha_{i1} p_{i1}^{(k)} } ,\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {\alpha_{i2} p_{i2}^{(k)} } , \ldots ,\frac{1}{{p\_{\text{size}}}}\sum\limits_{i = 1}^{{p\_{\text{size}}}} {\alpha_{in} p_{in}^{(k)} } } \right\} \\ \end{aligned} $$

(B.7)

where $\alpha_{i}$ is the weighted coefficient and $\alpha_{id}$ is the dimension coefficient of every particle. In this work, the weighted coefficient for each particle decreases linearly from 1.5 to 0.5.

On the other hand, according to Coelho (2010) in GQPSO, $\tilde{p}_{ij}^{(k)}$ is calculated as follows:

$$ \tilde{p}_{ij}^{(k)} = \frac{{\left\{ {Gp_{ij}^{(k)} + gp_{gj}^{(k)} } \right\}}}{{\left( {G + g} \right)}},\quad j = 1,2,3, \ldots ,n $$

(B.8)

where G and g be the random numbers which are generated using the absolute value of the Gaussian probability distribution with zero mean and unit variance.

$$ \begin{aligned} m^{(k)} & = \left( {m_{1}^{(k)} ,m_{2}^{(k)} , \ldots ,m_{n}^{(k)} } \right) \\ & = \left\{ {\frac{1}{p\_size}\sum\limits_{i = 1}^{p\_size} {p_{i1}^{(k)} } ,\frac{1}{p\_size}\sum\limits_{i = 1}^{p\_size} {p_{i2}^{(k)} } , \ldots ,\frac{1}{p\_size}\sum\limits_{i = 1}^{p\_size} {p_{in}^{(k)} } } \right\} \\ \end{aligned} $$

(B.9)

and the iterative equation for the position of the particle is given by

$$ x_{ij}^{(k)} = \tilde{p}_{ij}^{(k)} \pm \beta^{\prime}\left| {m_{j}^{(k)} - x_{ij}^{(k)} } \right|\log \left( {\frac{1}{G}} \right) $$

(B.10)

where $\beta^{\prime}$ decreases linearly from 1.0 to 0.5