Abstract
We investigate first-order separation logic with one record field restricted to a unique quantified variable (1SL1). Undecidability is known when the number of quantified variables is unbounded and the satisfiability problem is PSPACE-complete for the propositional fragment. We show that the satisfiability problem for 1SL1 is PSPACE-complete and we characterize its expressive power by showing that every formula is equivalent to a Boolean combination of atomic properties. This contributes to our understanding of fragments of first-order separation logic that can specify properties about the memory heap of programs with singly-linked lists. All the fragments we consider contain the magic wand operator and first-order quantification over a single variable.




Similar content being viewed by others
Notes
It is of course possible and perhaps more intuitive to define () using a quantifier by ∃ (↪), but that definition would not be correct for () because we are limited to the use of one quantified variable.
But in that case, we would have lost the expressivity characterisation of Theorem 4.11.
In the case of \(l/l^{\prime }\)for instance, we define
 . Then, by Proposition 2.24 applied to α and L
0, we chooseL and \(L^{\prime }\)such that \(L_{0} = L\uplus L^{\prime }\),\(L\sim _{\alpha } L\uplus L^{\prime }\)and\(\text {card}(L)\leqslant \alpha \).
. Then, by Proposition 2.24 applied to α and L
0, we chooseL and \(L^{\prime }\)such that \(L_{0} = L\uplus L^{\prime }\),\(L\sim _{\alpha } L\uplus L^{\prime }\)and\(\text {card}(L)\leqslant \alpha \).
References
Antonopoulos, T., Gorogiannis, N., Haase, C., Kanovich, M., Ouaknine, J.: Foundations for decision problems in separation logic with general inductive predicates. In: FOSSACS’14, Lecture Notes in Computer Science, vol. 8412, pp. 411–425. Springer (2014)
Bansal, K., Reynolds, A., King, T., Barrett, C., Wies, T.: Deciding local theory extensions via e-matching. In: CAV’15, Lecture Notes in Computer Science, vol. 9207, pp. 87–105. Springer (2015)
Barrett, C., Conway, C., Deters, M., Hadarean, L., Jovanovic, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: CAV’11, Lecture Notes in Computer Science, vol. 8606, pp. 171–177. Springer (2011)
Berdine, J., Calcagno, C., O’Hearn, P.: Smallfoot: modular automatic assertion checking with separation logic. In: FMCO’05, Lecture Notes in Computer Science, vol. 4111, pp. 115–137. Springer (2005)
Brochenin, R., Demri, S., Lozes, E.: Reasoning about sequences of memory states. Ann. Pure Appl. Logic 161(3), 305–323 (2009)
Brochenin, R., Demri, S., Lozes, E.: On the almighty wand. Inf. Comput. 211, 106–137 (2012)
Brotherston, J., Fuhs, C., Gorogiannis, N., Navarro Perez, J.: A decision procedure for satisfiability in separation logic with inductive predicates. In: CSL-LICS’14 (2014)
Brotherston, J., Kanovich, M.: Undecidability of propositional separation logic and its neighbours. In: LICS’10, pp. 130–139. IEEE (2010)
Calcagno, C., O’Hearn, P., Yang, H.: Computability and complexity results for a spatial assertion language for data structures. In: FSTTCS’01, Lecture Notes in Computer Science, vol. 2245, pp. 108– 119. Springer (2001)
Cook, B., Haase, C., Ouaknine, J., Parkinson, M., Worrell, J.: Tractable reasoning in a fragment of separation logic. In: CONCUR’11, Lecture Notes in Computer Science, vol. 6901, pp. 235–249. Springer (2011)
Dawar, A., Gardner, P., Ghelli, G.: Expressiveness and complexity of graph logic. Inf. Comput. 205(3), 263–310 (2007)
Demri, S., Deters, M.: Expressive completeness of separation logic with two variables and no separating conjunction. In: CSL-LICS’14. ACM Press (2014)
Demri, S., Galmiche, D., Larchey-Wendling, D., Méry, D.: Separation logic with one quantified variable. In: CSR’14, Lecture Notes in Computer Science, vol. 8476, pp. 125–138. Springer (2014)
Galmiche, D., Méry, D.: Tableaux and resource graphs for separation logic. J. Log. Comput. 20(1), 189–231 (2010)
Haase, C., Ishtiaq, S., Ouaknine, J., Parkinson, M.: SeLoger: a tool for graph-based reasoning in separation logic. In: CAV’13, Lecture Notes in Computer Science, vol. 8044, pp. 790–795. Springer (2013)
Iosif, R., Rogalewicz, A., Simacek, J.: The tree width of separation logic with recursive definitions. In: CADE’13, Lecture Notes in Computer Science, vol. 7898, pp. 21–38. Springer (2013)
Ishtiaq, S., O’Hearn, P.: BI as an assertion language for mutable data structures. In: Hankin, C., Schmidt, D. (eds.) POPL’01, pp. 14–26. ACM (2001)
Larchey-Wendling, D., Galmiche, D.: The undecidability of Boolean BI through phase semantics. In: LICS’10, pp. 140–149. IEEE (2010)
Lozes, E.: Expressivité des logiques spatiales. Ph.D. Thesis, LIP, ENS Lyon, France (2004)
Lozes, E.: Separation logic preserves the expressive power of classical logic. In: 2nd Workshop on Semantics, Program Analysis, and Computing Environments for Memory Management (SPACE’04) (2004)
de Moura, L., Björner, N.: Z3: an efficient SMT solver. In: TACAS’08, Lecture Notes in Computer Science, vol. 4963, pp. 337–340. Springer (2008)
Pérez, J. N., Rybalchenko, A.: Separation logic modulo theories. In: APLAS’13, Lecture Notes in Computer Science, vol. 8301, pp. 90–106 (2013)
Piskac, R., Wies, T., Zufferey, D.: Automating separation logic using SMT. In: CAV’13, Lecture Notes in Computer Science, vol. 2013, pp. 773–789. Springer (2013)
Piskac, R., Wies, T., Zufferey, D.: GRASShopper - complete heap verification with mixed specifications. In: TACAS’14, Lecture Notes in Computer Science, vol. 8413, pp. 124–139. Springer (2014)
Presburger, M.: Über Die Vollständigkeit Eines Gewissen Systems Der Arithmetik Ganzer Zahlen, in Welchem Die Addition Als Einzige Operation Hervortritt. In: Comptes Rendus Du Premier Congrès De Mathématiciens Des Pays Slaves, Warszawa, pp. 92–101 (1929)
Reynolds, J.: Separation logic: a logic for shared mutable data structures. In: LICS’02, pp. 55–74. IEEE (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
Work partially supported by the ANR grant DynRes (project No. ANR-11-BS02-011) and by the EU Seventh Framework Programme under grant agreement No. PIOF-GA-2011-301166 (DATAVERIF). Revised and complete version of [13].
Appendices
Appendix A: Proofs of Section 2
Proposition 2.9
Let
s, h, h
1, h
2
be such
that
 and let i ∈ [1, q]. The following identities hold:
and let i ∈ [1, q]. The following identities hold:
-
1.
\(\text {pred}_{\overline {\heartsuit }}(s , h_{1},i) = (\text {pred}_{\overline {\heartsuit }}(s ,h,i)\cap \text {dom}(h_{1}))\uplus (\text {pred}(s ,h,i)\cap {\Delta }(s , h_{1}, h_{2}))\);
-
2.
\(\text {loop}_{\overline {\heartsuit }}(s , h_{1}) = (\text {loop}_{\overline {\heartsuit }}(s ,h)\cap \text {dom}(h_{1}))\uplus (\text {loop}(s ,h)\cap {\Delta }(s , h_{1}, h_{2}))\);
-
3.
\(\text {rem}_{\overline {\heartsuit }}(s , h_{1}) = (\text {rem}_{\overline {\heartsuit }}(s ,h)\cap \text {dom}(h_{1}))\uplus (\text {rem}(s ,h)\cap {\Delta }(s , h_{1}, h_{2}))\).
Proof
First, observe that we have the following identities:
By definition, we have
Hence,
Consequently,
since\({\Delta }(s, h_{1}, h_{2}) \subseteq \text {dom}(h_{1})\). The other identities are established in a similar fashion. □
Proposition 2.10
Let (s, h) be a
memory state,
\( l_{1}\in \mathbb {N}\setminus \text {dom}(h) \)
and
\(l_{2}\in \mathbb {N}\). Let us
write
\(h_{1\rightarrow 2}\)
for
 and let i be in [1, q]. The following identities hold:
and let i be in [1, q]. The following identities hold:
Proof
The proof of the first four identities is left to the reader. For the identity that describes\(\heartsuit (s, h_{1\rightarrow 2})\), we noticethat
holds. For\(\text {acc}(s,h_{1\rightarrow 2})\), it is a bit more complicated. We have
Hence we deduce the properties:
- (P1):
-
\(\text {acc}(s,h)\subseteq \text {acc}(s,h_{1\rightarrow 2})\subseteq \text {acc}(s,h)\cup \{ l_{1}, l_{2}\}\);
- (P2):
-
\( l_{1}\in \text {acc}(s,h_{1\rightarrow 2})\setminus \text {acc}(s,h)\) iff \(l_{1}\in h(s(\mathcal {V}))\) or \( l_{1}= l_{2}\in s(\mathcal {V})\);
- (P3):
-
\( l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\setminus \text {acc}(s,h)\) iff \( l_{1}= l_{2}\in h(s(\mathcal {V}))\) or \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {dom}(h)\cup \{ l_{1}\}\)
From \(\heartsuit (s,h_{1\rightarrow 2})=\text {ref}(s,h_{1\rightarrow 2})\cup \text {acc}(s,h_{1\rightarrow 2})\), it is then easy to deduce the inclusions
Then we study the statements \(l_{1}\in \heartsuit (s,h_{1\rightarrow 2})\) and \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\) according to the four supplementary conditions on the right-hand side of the fifth identity:
-
if \( l_{1}\in s(\mathcal {V})\), l 2 ∈ dom(h) and l 2 ∉ ♡(s, h) then l 1 ≠ l 2 (because l 1 ∉ dom(h)). Then l 1, l 2 ∉ ♡(s, h). Hence the union ♡(s, h) ⊎ {l 1, l 2} is indeed disjoint. From \( l_{1}\in s(\mathcal {V})\) we deduce \(l_{1}\in \text {ref}(s,h_{1\rightarrow 2})\). From \( l_{1}\in s(\mathcal {V})\) and l 2 ∈ dom(h) we deduce \( l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\).
We obtain \(\heartsuit (s,h_{1\rightarrow 2})= \heartsuit (s, h)\uplus \{ l_{1}, l_{2}\}\);
-
if \( l_{1}\in s(\mathcal {V})\) and (l 2 ∉ dom(h) or l 2 ∈ ♡(s, h)) then we already have \( l_{1}\in \text {ref}(s,h_{1\rightarrow 2})\) and l 1 ∉ ♡(s, h). Hence \(l_{1}\in \heartsuit (s,h_{1\rightarrow 2})\setminus \heartsuit (s, h)\).
Let us show that if l 1≠l 2 and \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\) then l 2 ∈ ♡(s, h). By contradiction, let us assume l 1 ≠ l 2 and \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\setminus \heartsuit (s, h)\). Then we have \( l_{2}\in \text {ref}(s,h_{1\rightarrow 2})\cup \text {acc}(s,h_{1\rightarrow 2})\). Then either \(l_{2} \in \text {ref}(s,h_{1\rightarrow 2})\) or \( l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\). In the former case, from l 1 ≠ l 2 we deduce \( l_{2}\in \text {ref}(s,h)\subseteq \heartsuit (s, h)\), a contradiction. In the later case, we deduce \(l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\setminus \heartsuit (s, h)\subseteq \text {acc}(s,h_{1\rightarrow 2}) \setminus \text {acc}(s,h)\) hence, by (P3) either \( l_{1}= l_{2}\in h(s(\mathcal {V}))\) (a contradiction) or \(l_{2}\in \text {dom}(h)\cup \{ l_{1}\}\). From l 1 ≠ l 2, we get l 2 ∈ dom(h). Since we also have l 2 ∉ ♡(s, h), we get a contradiction with l 2 ∉ dom(h) or l 2 ∈ ♡(s, h).
We deduce \(\heartsuit (s,h_{1\rightarrow 2})= \heartsuit (s, h)\uplus \{ l_{1}\}\);
-
if \( l_{1}\not \in s(\mathcal {V})\) and \( l_{1}\in h(s(\mathcal {V}))\) then we have \(l_{1}\in \text {acc}(s,h_{1\rightarrow 2})\) and l 1 ∉ ♡(s, h). Hence we obtain \(l_{1}\in \heartsuit (s,h_{1\rightarrow 2})\setminus \heartsuit (s, h)\).
Let us show that if l 1 ≠ l 2 and \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\) then l 2 ∈ ♡(s, h). By contradiction, let us assume l 1 ≠ l 2 and \(l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\setminus \heartsuit (s, h)\). Then we have \(l_{2}\in \text {ref}(s,h_{1\rightarrow 2})\cup \text {acc}(s,h_{1\rightarrow 2})\). Then either \( l_{2}\in \text {ref}(s,h_{1\rightarrow 2})\) or \( l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\). But \(l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\) implies \( l_{2}\in \text {acc}(s,h_{1\rightarrow 2})\setminus \heartsuit (s, h) \subseteq \text {acc}(s,h_{1\rightarrow 2})\setminus \text {acc}(s,h)\) and thus, by (P3) we get either l 1 = l 2 (a contradiction) or \( l_{1}\not \in s(\mathcal {V})\) (a contradiction). From \( l_{2}\in \text {ref}(s,h_{1\rightarrow 2})\) and l 1 ≠ l 2 we deduce \(l_{2}\in \text {ref}(s,h)\subseteq \heartsuit (s, h)\) (a contradiction).
We obtain \(\heartsuit (s,h_{1\rightarrow 2})= \heartsuit (s, h)\uplus \{ l_{1}\}\);
-
if \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\) then neither l 1 nor l 2 belong to \(\text {acc}(s,h_{1\rightarrow 2})\setminus \text {acc}(s,h)\). Then \( l_{1}\in \text {ref}(s,h_{1\rightarrow 2})\) implies \( l_{1}\in s(\mathcal {V})\) which contradicts \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\). Hence we get \( l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\). Finally, \( l_{2}\in \text {ref}(s,h_{1\rightarrow 2})\) implies either l 2 ∈ ref(s, h) or l 1 = l 2. In the former case, we get l 2 ∈ ♡(s, h). In the later case, we have already proved \( l_{2}= l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\). Hence in any case, (\(l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\) and \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\)) imply l 2 ∈ ♡(s, h).
We obtain \(\heartsuit (s,h_{1\rightarrow 2})= \heartsuit (s, h)\).
□
Proposition 2.11
Let (s, h) be a
memory state,
\( l_{1}\in \mathbb {N}\setminus \text {dom}(h) \)
and
\( l_{2}\in \mathbb {N}\). Let us write
\( h_{1\rightarrow 2}\)
for
 and let i be in [1, q]. The following identities hold:
and let i be in [1, q]. The following identities hold:
where X −{l 2}means thatthe location l 2already belongs to the set X and is (strictly) removed from it.
Proof
Let us first establish the two following properties:
- (P1):
-
\( l_{1}\in \heartsuit (s,h_{1\rightarrow 2})\)iff \(l_{1}\in \mathfrak {p}\heartsuit (s,h)\);
- (P2):
-
if l 2 ∈ dom(h)∖♡(s, h) then (\( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\) iff \( l_{1}\in s(\mathcal {V})\)).
Property (P1) is a direct consequence of the last equation of Proposition 2.10 and the fact that l 1 ∉ ♡(s, h) (remember l 1 ∉ dom(h)). Let us prove Property (P2):
-
for the only if part, we assume \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\) and prove \( l_{1}\in s(\mathcal {V})\) by contradiction. Indeed, if \( l_{1}\not \in s(\mathcal {V})\), then we have the inclusion \(l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\subseteq \heartsuit (s, h)\cup \{ l_{1}\}\) according to Proposition 2.10. Hence either l 2 ∈ ♡(s, h) which contradicts l 2 ∈ dom(h)∖♡(s, h) or l 2 = l 1 which implies l 2 ∉ dom(h) and contradicts l 2 ∈ dom(h)∖♡(s, h);
-
for the if part, if \( l_{1}\in s(\mathcal {V})\) then \( l_{2}=h_{1\rightarrow 2}(l_{1})\in h_{1\rightarrow 2}(s(\mathcal {V}))\). Since \(l_{2}\in \text {dom}(h)\subseteq \text {dom}(h_{1\rightarrow 2})\) we deduce \(l_{2} \in \heartsuit (s,h_{1\rightarrow 2})\).
By Proposition 2.10, there are only three possible values for \(\heartsuit (s,h_{1\rightarrow 2})\):
Let us now consider the case of \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\). According to Proposition 2.10 and l 1 ∉ dom(h), we know that
Hence there are only three possible values for \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\): \(\text {pred}_{\overline {\heartsuit }}(s,h,i)\uplus \{ l_{1}\}\), \(\text {pred}_{\overline {\heartsuit }}(s,h,i)- \{l_{2}\}\) and \(\text {pred}_{\overline {\heartsuit }}(s,h,i)\); and we study those three cases:
-
\(l_{1}\in \text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\setminus \text {pred}_{\overline {\heartsuit }}(s,h,i)\) iff \(l_{1}\in \text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\) iff both \(l_{1}\in \text {pred}(s,h_{1\rightarrow 2},i)\) and \( l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\) iff both l 2 = s( i ) and \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\);
-
if \(l_{2}\in \text {pred}_{\overline {\heartsuit }}(s,h,i)\setminus \text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\) then \(l_{2}\in \text {pred}_{\overline {\heartsuit }} (s,h,i)\) and either \( l_{2}\not \in \text {pred}(s,h_{1\rightarrow 2},i)\) or \(l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\). But \(\text {pred}_{\overline {\heartsuit }}(s,h,i) \subseteq \text {pred}(s,h,i)\subseteq \text {pred}(s, h_{1\rightarrow 2},i)\). Hence we get \( l_{2}\in \text {pred}(s,h_{1\rightarrow 2},i)\) and thus we must have \(l_{2} \in \heartsuit (s,h_{1\rightarrow 2})\). Since \(l_{2}\in \text {pred}_{\overline {\heartsuit }}(s,h,i) \subseteq \text {dom}(h)\setminus \heartsuit (s, h)\) we deduce \( l_{1}\in s(\mathcal {V})\) by Property (P2);
-
if \(l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {pred}_{\overline {\heartsuit }}(s,h,i)\) then \(l_{2}\in h_{1\rightarrow 2}(s(\mathcal {V}))\cap \text {dom}(h)\subseteq \heartsuit (s,h_{1\rightarrow 2})\). Hence we get \(l_{2} \not \in \text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)\).
Let us now consider the case of \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\). According to Proposition 2.10, we know that
and by inclusion (A.1), we deduce that there are only three possible values for \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\) which are \(\text {loop}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\), \(\text {loop}_{\overline {\heartsuit }}(s,h)-\{ l_{2}\}\) and \(\text {loop}_{\overline {\heartsuit }}(s,h)\).
-
\(l_{1}\in \text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\setminus \text {loop}_{\overline {\heartsuit }}(s,h)\) iff \( l_{1}\in \text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\) iff \(l_{1}\in \text {loop}(s,h_{1\rightarrow 2})\) and \( l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\) iff l 1 = l 2 and \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\);
-
if \(l_{2}\in \text {loop}_{\overline {\heartsuit }}(s,h)\setminus \text {loop}_{\overline {\heartsuit }} (s,h_{1\rightarrow 2})\) then we have \( l_{2}\in \text {loop}_{\overline {\heartsuit }}(s,h)\) and either \(l_{2}\not \in \text {loop}(s,h_{1\rightarrow 2})\) or \(l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\). But \(\text {loop}_{\overline {\heartsuit }}(s,h) \subseteq \text {loop}(s,h_{1\rightarrow 2})\). Hence we get \(l_{2}\in \text {loop}(s,h_{1\rightarrow 2})\) and thus we must have \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\). Since \(l_{2}\in \text {loop}_{\overline {\heartsuit }}(s,h)\subseteq \text {dom}(h)\setminus \heartsuit (s, h)\) we deduce \(l_{1}\in s(\mathcal {V})\)by Property (P2);
-
if \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {loop}_{\overline {\heartsuit }}(s,h)\) then \(l_{2}\in h_{1\rightarrow 2}(s(\mathcal {V}))\cap \text {dom}(h)\subseteq \heartsuit (s,h_{1\rightarrow 2})\). Hence we get \(l_{2} \not \in \text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\).
Let us now consider the case of \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\).According to Proposition 2.10, we knowthat
and by inclusion (A.1), we deduce that there are only three possible values for \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\) which are \(\text {rem}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\), \(\text {rem}_{\overline {\heartsuit }}(s,h)-\{ l_{2}\}\) and \(\text {rem}_{\overline {\heartsuit }}(s,h)\).
-
\(l_{1}\in \text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\setminus \text {rem}_{\overline {\heartsuit }}(s,h)\) iff \( l_{1}\in \text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\) iff \(l_{1}\in \text {rem}(s,h_{1\rightarrow 2})\) and \( l_{1}\not \in \heartsuit (s,h_{1\rightarrow 2})\) iff \(l_{2}\not \in s(\mathcal {V})\cup \{ l_{1}\}\) and \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\);
-
if \(l_{2}\in \text {rem}_{\overline {\heartsuit }}(s,h)\setminus \text {rem}_{\overline {\heartsuit }} (s,h_{1\rightarrow 2})\) then \(l_{2}\in \text {rem}_{\overline {\heartsuit }}(s,h)\) and either \(l_{2}\not \in \text {rem}(s, h_{1\rightarrow 2})\) or \(l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\). Because of the inclusions \(\text {rem}_{\overline {\heartsuit }}(s,h) \subseteq \text {rem}(s,h) \subseteq \text {rem}(s,h_{1\rightarrow 2})\), we have \( l_{2}\in \text {rem}(s,h_{1\rightarrow 2})\) and thus we deduce \( l_{2}\in \heartsuit (s,h_{1\rightarrow 2})\). Since \(l_{2}\in \text {rem}_{\overline {\heartsuit }}(s,h)\subseteq \text {dom}(h)\setminus \heartsuit (s, h)\) we deduce \(l_{1}\in s(\mathcal {V})\)by Property (P2);
-
if \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {rem}_{\overline {\heartsuit }}(s,h)\) then \(l_{2}\in h_{1\rightarrow 2}(s(\mathcal {V}))\cap \text {dom}(h)\subseteq \heartsuit (s,h_{1\rightarrow 2})\). Hence we get \(l_{2} \not \in \text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\).
□
Lemma 2.14
For any \(k\geqslant 1\) and for any i ∈ [1,q], there exist 1SL1 formulæ denoted \(\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant k\),\(\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant k\) and \(\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant k\) respectively such that, for any memory state (s, h) and for any location \( l \in \mathbb {N}\) the following equivalences hold:
-
1.
\((s,h) \models _{l } \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant k\text { iff } \text {card}(\text {pred}_{\overline {\heartsuit }}(s , h ,i))\geqslant k\) ;
-
2.
\((s,h) \models _{l } \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant k\text { iff } \text {card}(\text {loop}_{\overline {\heartsuit }}(s , h ))\geqslant k\) ;
-
3.
\((s,h) \models _{l } \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant k\text { iff } \text {card}(\text {rem}_{\overline {\heartsuit }}(s , h ))\geqslant k\) .
Proof
Let us first establish the equivalence
For the if part, let us assume \(\text {card}(\text {pred}_{\heartsuit }(s,h,j))\geqslant k\). Then, let us define
We also recall the notations s R = {s(x i ) ∣ i ∈ R} and s A = {s(x i ) ∣ i ∈ A} from Proposition 2.13. We check the identities pred♡(s, h, j) = s R ⊎ h(s A), card(s R) = card(R) and card(h(s A)) = card(A) hold. We deduce \(\text {card}(R)+\text {card}(A) \geqslant k\). By Proposition 2.13, we have (s, h) ⊧ l R and (s, h) ⊧ l acc A . For any r ∈ R we have h(s(x r )) = s(x j ) hence \((s,h)\models _{l}\bigwedge _{r\in R}\mathtt {x}_{r}\hookrightarrow \mathtt {x}_{j}\). For any a ∈ A we have \(h^{2}(s(\mathtt {x}_a))= s(\mathtt {x}_{j})\) hence \((s,h)\models _{l}\bigwedge _{a\in A}\mathtt {btwn}(\mathtt {x}_{a},\mathtt {x}_{j})\).
For the only if part, let us assume \((s,h)\models _{l}\#\mathtt {pred}_{{\heartsuit }} (\mathtt {x}_{j}) \geqslant k\). By definition, there exist \(R,A\subseteq [1,q]\) such that \(\text {card}(R)+\text {card}(A)\geqslant k\), (s, h) ⊧ l ref R , (s, h) ⊧ l acc A , ∀r ∈ R, h(s(x r )) = s(x j ) and \(\forall a\in A,\, h^{2}(s(\mathtt {x}_a))= s(\mathtt {x}_{j})\). We deduce the inclusions \(sR\subseteq \text {pred}(s,h,j)\cap \text {ref}(s,h)\) and \( h(sA)\subseteq \text {pred}(s,h,j)\cap (\text {acc}(s,h)\setminus \text {ref}(s,h))\) as well as the identities card(s R) = card(R) and card(h(s A)) = card(A). Hence \(sR\uplus h(sA)\subseteq \text {pred}_{\heartsuit }(s,h,j)\) and \(\text {card}(sR\uplus h(sA))=\text {card}(R)+\text {card}(A)\geqslant k\). As a consequence, the relation \(\text {card}(\text {pred}_{\heartsuit }(s,h,j))\geqslant k\) holds.
Let us now establish the equivalence
For the if part, let us assume \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))\geqslant k\). Let us define p = card(pred♡(s, h, j)). From \(\text {pred}_{\heartsuit }(s,h,j)\subseteq \heartsuit (s, h)\) we deduce \(p\leqslant 2q\). We have card(pred♡(s, h, j)) = p < p + 1 and as a consequence, we deduce \((s,h)\nvDash _{l}\#\mathtt {pred}_{\heartsuit }(\mathtt {x}_{j})\geqslant p+1\). From \(\text {pred}(s,h,j)=\text {pred}_{\heartsuit }(s,h,j)\uplus \text {pred}_{\overline {\heartsuit }}(s,h,j)\) we get \(\text {card}(\text {pred}(s,h,j))\geqslant k+p\) and thus the relation \((s,h)\models _{l}\#\mathtt {pred}(\mathtt {x}_{j})\geqslant k+p\) holds. We deduce \((s,h)\models _{l}\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant k\).
For the only if part, let us assume \((s,h)\models _{l}\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j}) \geqslant k\). There exists \(p\leqslant 2q\) such that \((s,h)\models _{l}\#\mathtt {pred}(\mathtt {x}_{j})\geqslant k+p\) and \((s,h)\nvDash _{l}\#\mathtt {pred}_{\heartsuit }(\mathtt {x}_{j})\geqslant p+1\). We deduce the upperbound \(\text {card} (\text {pred}_{\heartsuit }(s,h,j))\leqslant p\) and the lowerbound \(\text {card}(\text {pred}(s,h,j))\geqslant k+p\). Using the partition \(\text {pred}(s,h,j)=\text {pred}_{\heartsuit }(s,h,j)\uplus \text {pred}_{\overline {\heartsuit }} (s,h,j)\), we derive the lower bound \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))\geqslant k\).
The cases of the test formulæ \(\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant k\) and \(\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant k\) can be treated in a similar way after slight modifications in the definitions of R and A. □
Lemma 2.21
Let \(\alpha _{1},\alpha _{2} \in \mathbb {N}\) and \(X, X^{\prime }, Y_{0}\) be finite sets such that \(X \uplus X^{\prime } \sim _{\alpha _{1}+\alpha _{2}} Y_{0}\) holds. Then there are two finite sets \(Y, Y^{\prime }\) such that \(Y_{0} =Y \uplus Y^{\prime }\), \(X \sim _{\alpha _{1}} Y\) and \(X^{\prime } \sim _{\alpha _{2}} Y^{\prime }\) hold.
Proof
By Proposition 2.18 item 3, we have two cases: either \(\text {card}(X\uplus X^{\prime })=\text {card}(Y_{0})< \alpha _{1}+\alpha _{2}\) or \(\text {card}(X\uplus X^{\prime })\geqslant \alpha _{1}+\alpha _{2}\) and \(\text {card}(Y_{0}) \geqslant \alpha _{1}+\alpha _{2}\).
The case \(\text {card}(X\uplus X^{\prime })=\text {card}(Y_{0})<\alpha _{1}+\alpha _{2}\) is easy: we have \(\text {card}(X) \leqslant \text {card}(X)+\text {card}(X^{\prime })=\text {card}(Y_{0})\); then for Y, we choose any subset of Y 0 such that card(Y) = card(X). Then we define \(Y^{\prime }=Y_{0}\setminus Y\) and we get \(\text {card}(Y^{\prime })=\text {card}(Y_{0})-\text {card}(Y)=\text {card}(X\uplus X^{\prime })- \text {card}(X)=\text {card}(X^{\prime })\). Then we have both \(X\sim _{\alpha _{1}} Y\) and \(X^{\prime }\sim _{\alpha _{2}} Y^{\prime }\).
Let us consider the case \(\text {card}(X\uplus X^{\prime })\geqslant \alpha _{1}+\alpha _{2}\) and \(\text {card}(Y_{0}) \geqslant \alpha _{1}+\alpha _{2}\). We have four sub-cases:
-
the case card(X) < α 1 and \(\text {card}(X^{\prime })<\alpha _{2}\) is impossible because it contradicts \(\text {card}(X\uplus X^{\prime })\geqslant \alpha _{1}+\alpha _{2}\);
-
in the case \(\text {card}(X)\geqslant \alpha _{1}\) and \(\text {card}(X^{\prime })<\alpha _{2}\), let \(Y^{\prime }\) be any subset of Y 0 such that \(\text {card}(Y^{\prime })=\text {card}(X^{\prime })\) and \(Y=Y_{0}\setminus Y^{\prime }\). We have \(\text {card}(X^{\prime })=\text {card}(Y^{\prime })\) hence \(X^{\prime }\sim _{\alpha _{2}} Y^{\prime }\). We have \(\text {card}(X)\geqslant \alpha _{1}\) and \(\text {card}(Y)=\text {card}(Y_{0})-\text {card}(Y^{\prime })\geqslant (\alpha _{1}+\alpha _{2})-\alpha _{2}=\alpha _{1}\) hence \(X\sim _{\alpha _{1}} Y\);
-
the case card(X) < α 1 and \(\text {card}(X^{\prime })\geqslant \alpha _{2}\) is obtained by symmetry from the previous case;
-
in the case \(\text {card}(X)\geqslant \alpha _{1}\) and \(\text {card}(X^{\prime })\geqslant \alpha _{2}\), let Y be any subset of Y 0 s.t. card(Y ) = α 1 and \(Y^{\prime }=Y_{0}\setminus Y\). We have \(\text {card}(X)\geqslant \alpha _{1}\) and card(Y) = α 1 hence \(X\sim _{\alpha _{1}} Y\). We have \(\text {card}(X^{\prime })\geqslant \alpha _{2}\) and \(\text {card}(Y^{\prime })=\text {card}(Y_{0})-\text {card}(Y)\geqslant (\alpha _{1}+\alpha _{2})-\alpha _{1}=\alpha _{2}\) hence \(X^{\prime }\sim _{\alpha _{2}} Y^{\prime }\).
□
Appendix B: Proofs of Section 3
Proposition 3.13
Let \(u,v\in \mathbb {N}\). For \((\mathfrak {T}10)\) – \((\mathfrak {T}20)\) defined as
- \((\mathfrak {T}10)\) :
-
\(u\in s (\mathcal {V})\) iff \(v\in s^{\prime }(\mathcal {V})\) ;
- \((\mathfrak {T}11)\) :
-
\(u\in h (s (\mathcal {V}))\) iff \(v\in h^{\prime }(s^{\prime }(\mathcal {V}))\) ;
- \((\mathfrak {T}12)\) :
-
\(u\in \mathfrak {p}\heartsuit (s , h )\) iff \(v\in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}13)\) :
-
u ∈♡(s, h)iff \(v\in \heartsuit (s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}14)\) :
-
u ∈pred(s, h, i)iff \(v\in \text {pred}(s^{\prime }, h^{\prime },i)\) for any i ∈ [1,q];
- \((\mathfrak {T}15)\) :
-
u ∈pred(s, h)iff \(v\in \text {pred}(s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}16)\) :
-
u ∈loop(s, h)iff \(v\in \text {loop}(s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}17)\) :
-
u ∈rem(s, h)iff \(v\in \text {rem}(s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}18)\) :
-
\(u\in \text {pred}_{\overline {\heartsuit }}(s , h ,i)\) iff \(v\in \text {pred}_{\overline {\heartsuit }}(s^{\prime }, h^{\prime },i)\) for any i ∈ [1,q];
- \((\mathfrak {T}19)\) :
-
\(u\in \text {loop}_{\overline {\heartsuit }}(s , h )\) iff \(v\in \text {loop}_{\overline {\heartsuit }}(s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}20)\) :
-
\(u\in \text {rem}_{\overline {\heartsuit }}(s , h )\) iff \(v\in \text {rem}_{\overline {\heartsuit }}(s^{\prime }, h^{\prime })\) ;
- \((\mathfrak {T}21)\) :
-
\(u\in \mathfrak {p}\heartsuit (\mathfrak {m})\) iff \(v\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) .
the following propositions hold:
-
1. \((\mathfrak {T}2)\) implies \((\mathfrak {T}10)\) ; 4. \((\mathfrak {T}2\) – 4) imply \((\mathfrak {T}13)\);
-
2. \((\mathfrak {T}3)\) implies \((\mathfrak {T}11)\) ; 5. \((\mathfrak {T}2\) – 6) imply \((\mathfrak {T}10\) – 20);
-
3. \((\mathfrak {T}2\) – 3) imply \((\mathfrak {T}12)\) ; 6. \((\mathfrak {T}1\) – 3) imply \((\mathfrak {T}21)\).
Proof
The proofs are easy. Here is a summary of the arguments:
- \((\mathfrak {T}10)\) :
-
is a direct consequence of \((\mathfrak {T}2)\);
- \((\mathfrak {T}11)\) :
-
is a direct consequence of \((\mathfrak {T}3)\);
- \((\mathfrak {T}12)\) :
-
we use the identity \(\mathfrak {p}\heartsuit (s,h)= s(\mathcal {V})\cup h(s(\mathcal {V}))\),\((\mathfrak {T}10)\)and \((\mathfrak {T}11)\);
- \((\mathfrak {T}13)\) :
-
we use the identity \(\heartsuit (s,h)=\mathfrak {p}\heartsuit (s,h)\cap \text {dom}(h)\),\((\mathfrak {T}12)\)and \((\mathfrak {T}4)\);
- \((\mathfrak {T}14)\) :
-
just another way to write \((\mathfrak {T}5)\);
- \((\mathfrak {T}15)\) :
-
we use the identity \(\text {pred}(s,h)=\bigcup _{i}\text {pred}(s,h,i)\)and \((\mathfrak {T}14)\);
- \((\mathfrak {T}16)\) :
-
just another way to write \((\mathfrak {T}6)\);
- \((\mathfrak {T}17)\) :
-
with \(\text {rem}(s,h)=\text {dom}(h)\setminus (\text {pred}(s,h)\cup \text {loop}(s,h))\),\((\mathfrak {T}4)\),\((\mathfrak {T}15)\),\((\mathfrak {T}16)\);
- \((\mathfrak {T}18)\) :
-
we use \(\text {pred}_{\overline {\heartsuit }}(s,h,i)=\text {pred}(s,h,i)\setminus \mathfrak {p}\heartsuit (s,h)\)and \((\mathfrak {T}14)\),\((\mathfrak {T}12)\);
- \((\mathfrak {T}19)\) :
-
we use \(\text {loop}_{\overline {\heartsuit }}(s,h)=\text {loop}(s,h)\setminus \mathfrak {p}\heartsuit (s,h)\)and \((\mathfrak {T}16)\),\((\mathfrak {T}12)\);
- \((\mathfrak {T}20)\) :
-
we use \(\text {rem}_{\overline {\heartsuit }}(s,h)=\text {rem}(s,h)\setminus \mathfrak {p}\heartsuit (s,h)\)and (T17),\((\mathfrak {T}12)\);
- \((\mathfrak {T}21)\) :
-
we use the identity \(\mathfrak {p}\heartsuit (\mathfrak {m})=\mathfrak {p}\heartsuit (s,h)\cup \{l\}\),\((\mathfrak {T}12)\)and \((\mathfrak {T}1)\).
□
Proposition 3.15
The following inclusions hold:
Proof
Inclusions 1 and 4 are trivial. Let us consider Inclusion 2, hence let u and v be such that \(u\mathfrak {T} v\) and \(u\in \mathfrak {p}\heartsuit (s,h)\). Since \(\mathfrak {p}\heartsuit (s,h)= s(\mathcal {V})\cup h(s(\mathcal {V}))\) we have two cases:
-
either u = s(x i ) for some i ∈ [1, q] and then \(v= s^{\prime }(\mathtt {x}_{i})\) by \((\mathfrak {T}2)\). Hence u and v satisfy \((\mathfrak {R}2)\) and thus we deduce \(u\mathfrak {R} v\);
-
or u = h(s(x i )) for some i ∈ [1, q] and then \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) by \((\mathfrak {T}3)\). Hence u and v satisfy \((\mathfrak {R}3)\) and thus we deduce \(u\mathfrak {R} v\).
Inclusions 3, 5 and 6 are proved in a similar way. □
Proposition 3.16
The following properties hold:
-
1.
The relation \(\mathfrak {T}\) restricted to \(\mathfrak {p}\heartsuit (s , h )\times \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\) is functional and injective.
-
2.
The relation \(\mathfrak {T}^{\text {\textsf {l}}}\) restricted to \(\mathfrak {p}\heartsuit (\mathfrak {m})\times \mathfrak {p} \heartsuit (\mathfrak {m}^{\prime })\) is functional and injective.
-
3.
For any \(u\not \in \text {dom}(h) \cup \mathfrak {p}\heartsuit (s , h )\), \(v\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\), we have \(u\mathfrak {T} v\).
-
4.
For any \(u\not \in \text {dom}(h) \cup \mathfrak {p}\heartsuit (\mathfrak {m})\), \(v\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\), we have \(u\mathfrak {T}^{\text {\textsf {l}}} v\) .
Proof
To show that \(\mathfrak {T}\) is functional, we prove that for all \(u\in \mathfrak {p}\heartsuit (s,h)\), for all \(v,w\in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\), \(u\mathfrak {T} v\) and \(u\mathfrak {T} w\) imply v = w. If u = s(x i ) then we must have \(v= s^{\prime }(\mathtt {x}_{i})=w\); and if u = h(s(x i )) then we must have \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))=w\). By symmetric arguments, \(\mathfrak {T}\) is injective. The proof that \(\mathfrak {T}^{\text {\textsf {l}}}\) restricted \(\mathfrak {p}\heartsuit (\mathfrak {m})\times \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) is functional and injective (Property 2) is similar.
Let us now establish Property 3. We consider \(u,v\in \mathbb {N}\) such that \(u\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (s,h)\) and \(v\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\). Conditions (\(\mathfrak {T}\)2–3) hold because \(u\not \in s(\mathcal {V}) \cup h(s(\mathcal {V}))\) and \(v\not \in s^{\prime }(\mathcal {V}) \cup h^{\prime }(s^{\prime }(\mathcal {V}))\). Conditions (\(\mathfrak {T}\)4–6) hold because u ∉ dom(h) and \(v\not \in \text {dom}(h^{\prime })\). The proof of Property 4 follows a similar pattern. □
Theorem 3.17
\(\mathfrak {m}\simeq _{b}\mathfrak {m}^{\prime }\) if and only if \({\mathfrak {R}^{\text {\textsf {l}}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\).
Proof
Let us show the only if part first. We assume \(\mathfrak {m}\simeq _{b}\mathfrak {m}^{\prime }\) and we prove \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) by case analysis on \(u\mathfrak {R}^{\text {\textsf {l}}} v\):
- \((\mathfrak {R}1)\) :
-
let us check \( l\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }\): Condition \(\mathfrak {T}1\) is trivial; for Condition \((\mathfrak {T}2)\), l = s(x j ) iff (s, h) ⊧ l x j = u iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{j}={\mathtt {u}}\) iff \( l^{\prime }= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}3)\), l = h(s(x j )) iff (s, h) ⊧ l x j ↪ u iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{j}\hookrightarrow {\mathtt {u}}\) iff \( l^{\prime }= h^{\prime }(s^{\prime }(\mathtt {x}_{j}))\); for Condition \((\mathfrak {T}4)\), l ∈ dom(h) iff (s, h) ⊧ l toalloc(u) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {toalloc}(\mathtt {u})\) iff \( l^{\prime }\in \text {dom}(h^{\prime })\); for Condition \((\mathfrak {T}5)\), h(l) = s(x j ) iff (s, h) ⊧ l ↪ u j iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\) iff \( h^{\prime }(l^{\prime })= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}6)\), h(l) = l iff (s, h) ⊧ l u ↪ u iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {u}}\) iff \( h^{\prime }(l^{\prime })= l^{\prime }\);
- \((\mathfrak {R}2)\) :
-
let us check \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\): for Condition \(\mathfrak {T}1\), s(x i ) = l iff \( s^{\prime }(\mathtt {x}_{i})= l^{\prime }\)(as previously); for Condition \((\mathfrak {T}2)\), s(x i ) = s(x j ) iff (s, h) ⊧ l x i = x j iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{i}={\mathtt {x}_{j}}\) iff \( s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}3)\), s(x i ) = h(s(x j )) iff (s, h) ⊧ l x j ↪ x i iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{j}\hookrightarrow {\mathtt {x}_{i}}\) iff \(s^{\prime }(\mathtt {x}_{i})= h^{\prime }(s^{\prime }(\mathtt {x}_{j}))\); for Condition \((\mathfrak {T}4)\), s(x i ) ∈ dom(h) iff (s, h) ⊧ l conv(x i , x i ) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{i})\) iff \( s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h^{\prime })\); for the proof of Condition \((\mathfrak {T}5)\), h(s(x i )) = s(x j ) iff (s, h) ⊧ l x i ↪ x j iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\) iff \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}6)\), h(s(x i )) = s(x i ) iff (s, h) ⊧ l x i ↪ x i iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{i}}\) iff \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= s^{\prime }(\mathtt {x}_{i})\);
- \((\mathfrak {R}3)\) :
-
let us check \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\): for Condition \(\mathfrak {T}1\), h(s(x i )) = l iff \(h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= l^{\prime }\) (as previously); for the proof of Condition \((\mathfrak {T}2)\), h(s(x i )) = s(x j ) iff (s, h) ⊧ l x i ↪ x j iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\) iff \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}3)\), h(s(x i )) = h(s(x j )) iff (s, h) ⊧ l conv(x i , x j ) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\) iff \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= h^{\prime }(s^{\prime }(\mathtt {x}_{j}))\); for Condition \((\mathfrak {T}4)\), h(s(x i )) ∈ dom(h) iff (s, h) ⊧ l toalloc( i ) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\) iff \(h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h^{\prime })\); for Condition \((\mathfrak {T}5)\), h(h(s(x i ))) = s(x j ) iff (s, h) ⊧ l btwn(x i , x j ) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\) iff \( h^{\prime }(h^{\prime }(s^{\prime }(\mathtt {x}_{i})))= s^{\prime }(\mathtt {x}_{j})\); for Condition \((\mathfrak {T}6)\), h(h(s(x i ))) = h(s(x i )) iff (s, h) ⊧ l toloop(x i ) iff \((s^{\prime },h^{\prime })\models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\) iff \( h^{\prime }(h^{\prime }(s^{\prime }(\mathtt {x}_{i})))= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\).
Let us now tackle the if part. We assume \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\). Hence we have \( l\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }\), \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\) for any i ∈ [1, q], and \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) for any i ∈ [1, q] such that s(x i ) ∈ dom(h) (and \( s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h^{\prime })\)). To establish \(\mathfrak {m}\simeq _{b}\mathfrak {m}^{\prime }\), we consider a formula B ∈ Basic and we show that (s, h) ⊧ l B implies \((s^{\prime },h^{\prime })\models _{l^{\prime }}B\). The reverse implication can be proved by symmetric arguments. We proceed by a case analysis on B:
- B is x i = x j ::
-
if (s, h) ⊧ l x i = x j then s(x i ) = s(x j ). Using the instance of \((\mathfrak {T}2)\) for \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\) with parameter j, we get \( s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}={\mathtt {x}_{j}}\);
- B is x i ↪ x j ::
-
if (s, h) ⊧ l x i ↪ x j then h(s(x i )) = s(x j ). Using the instance of \((\mathfrak {T}2)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) with parameter j, we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= s^{\prime }(\mathtt {x}_{j})\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\);
- B is conv(x i , x j )::
-
if (s, h) ⊧ l (x i , x j ) then h(s(x i )) = h(s(x j )). Using the instance of \((\mathfrak {T}3)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) with parameter j, we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= h^{\prime }(s^{\prime }(\mathtt {x}_{j}))\). We conclude with \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\);
- B is btwn( i , x j )::
-
if (s, h) ⊧ l btwn(x i , x j ) then h(h(s(x i ))) = s(x j ). Using the instance of \((\mathfrak {T}5)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) with parameter j, we get \( h^{\prime }(h^{\prime }(s^{\prime }(\mathtt {x}_{i})))= s^{\prime }(\mathtt {x}_{j})\). We conclude with \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\);
- B is toalloc( i )::
-
if (s, h) ⊧ l toalloc(x i ) then h(s(x i )) ∈ dom(h). With \((\mathfrak {T}4)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\), we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h^{\prime })\). We deduce \((s^{\prime },h^{\prime })\models _{l^{\prime }}\) toalloc(x i );
- B is toloop(x i )::
-
if (s, h) ⊧ l toloop(x i ) then h(h(s(x i ))) = h(s(x i )). By \((\mathfrak {T}6)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\), we get \( h^{\prime }(h^{\prime }(s^{\prime }(\mathtt {x}_{i})))= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\);
- B is u ↪ u::
-
if (s, h) ⊧ l u ↪ u then h(l) = l. Using \((\mathfrak {T}6)\) for \( l\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }\), we get \( h^{\prime }(l^{\prime })= l^{\prime }\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {u}}\);
- B is alloc(u)::
-
if (s, h) ⊧ l alloc(u) then l ∈ dom(h). Using \((\mathfrak {T}4)\) for \( l\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }\), we get \( l^{\prime }\in \text {dom}(h^{\prime })\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\);
- B is x i = u::
-
if (s, h) ⊧ l x i = u then s(x i ) = l. Using \((\mathfrak {T}1)\) for \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\), we get \( s^{\prime }(\mathtt {x}_{i})= l^{\prime }\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}=\mathtt {u}\);
- B is x i ↪ u::
-
if (s, h) ⊧ l x i ↪ u then h(s(x i )) = l. Using \((\mathfrak {T}1)\) for \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\), we derive \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= l^{\prime }\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {u}}\);
- B is u ↪ x i ::
-
if (s, h) ⊧ l ↪ x i then h(l) = s(x i ). Using \((\mathfrak {T}5)\) for \( l\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }\) with parameter i, we get \( h^{\prime }(l^{\prime })= s^{\prime }(\mathtt {x}_{i})\). We deduce \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{i}}\).
□
Proposition 3.18
If \(\mathfrak {m}\simeq _{b}\mathfrak {m}^{\prime }\) then the following properties hold:
-
1.
The relation \(\mathfrak {R}\) is total and surjective between \(\mathfrak {p}\heartsuit (s , h )\) and \(\mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\) ;
-
2.
The relation \(\mathfrak {R}^{\text {\textsf {l}}}\) is total and surjective between \(\mathfrak {p}\heartsuit (\mathfrak {m})\) and \(\mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) .
Proof
Let us consider Property 1. To show that \(\mathfrak {R}\) is total, we prove that for all \(u\in \mathfrak {p}\heartsuit (s,h)\), there is \(v\in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\) such that \(u\mathfrak {R} v\). If u = s(x i ) then choose \(v= s^{\prime }(\mathtt {x}_{i})\); and if u = h(s(x i )) then s(x i ) ∈ dom(h). But we have \( s(\mathtt {x}_{i})\mathfrak {R}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\) by definition of \(\mathfrak {R}^{\text {\textsf {l}}}\), hence by Theorem 3.17 we deduce \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\). As a consequence \(s(\mathtt {x}_{i})/ s^{\prime }(\mathtt {x}_{i})\) verify \((\mathfrak {T}4)\) and thus \(s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h^{\prime })\). We choose \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) and we get \(u\mathfrak {R}^{\text {\textsf {l}}} v\) and \(v\in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\).
By symmetric arguments, \(\mathfrak {R}\) is surjective. The proof that\(\mathfrak {R}^{\text {\textsf {l}}}\) is total and surjective (Property 2) is similar. □
Proposition 3.21
If \(\mathfrak {m}\) and \(\mathfrak {m}^{\prime }\) satisfy \(\mathfrak {m}\simeq _{1}\mathfrak {m}^{\prime }\), then \(\mathfrak {T}\) is a total relation on \(\mathbb {N}\) : for any \(u\in \mathbb {N}\), there exists \(v\leqslant \text {maxval}(s^{\prime }, h^{\prime })+1\) such that \(u\mathfrak {T} v\).
Proof
Since \({\simeq _{1}}\subseteq {\simeq _{b}}\) we have \({\mathfrak {R}}\subseteq {\mathfrak {T}}\) by Lemma 3.19. Letus consider \(u\in \mathbb {N}\). We have to show that there exists \(v\in \mathbb {N}\) such that \(u\mathfrak {T} v\) holds. We determine the value of v according to the first condition that holds in the following list:
- if \(u\in \mathfrak {p}\heartsuit (s,h)\) :
-
then let us define v to be the unique location in \(\mathfrak {p}\heartsuit (s^{\prime },h^{\prime })\) such that \(u\mathfrak {R} v\), see Lemma 3.19. We deduce \(u\mathfrak {T} v\). The relation \(v\leqslant \text {maxval}(s^{\prime },h^{\prime })+1\) holds because \(v\in \mathfrak {p}\heartsuit (s^{\prime },h^{\prime })\);
- if \(u\in \text {pred}_{\overline {\heartsuit }}(s,h,j)\) for some j ∈ [1, q]:
-
then we know that \(\text {pred}_{\overline {\heartsuit }}(s,h,j)\) is not empty. We deduce the equipotence \(\text {pred}_{\overline {\heartsuit }}(s,h,j) \simeq _{1}\text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },j)\) by Proposition 3.10 hence \(\text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },j)\) is not empty either. We choose any \(v\in \text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },j)\).
The relation \(v\leqslant \text {maxval}(s^{\prime },h^{\prime })+1\) holds because \(v\in \text {dom}(h^{\prime })\). Let us check that \(u\mathfrak {T} v\) holds by establishing Properties (\(\mathfrak {T}\)2–6) for u/v. We have \(u\in \text {pred}_{\overline {\heartsuit }}(s,h,j)\) and \(v\in \text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },j)\). As a consequence we deduce \(u\not \in \mathfrak {p}\heartsuit (s,h)\) and \(v\not \in \mathfrak {p}\heartsuit (s^{\prime },h^{\prime })\). Hence Properties (\(\mathfrak {T}\)2–3) hold. We also have u ∈ dom(h) and \(v\in \text {dom}(h^{\prime })\) hence Property \((\mathfrak {T}4)\) holds. We have h(u) = s(x j ) and \(h^{\prime }(v)=s^{\prime }(\mathtt {x}_{j})\). We deduce \(h(u)\mathfrak {R}h^{\prime }(v)\) and thus \(h(u)\mathfrak {T}h^{\prime }(v)\). Since \((\mathfrak {T}2)\) holds for \(h(u)/h^{\prime }(v)\), we deduce that Property \((\mathfrak {T}5)\) holds for u/v. Let us prove Property \((\mathfrak {T}6)\) for u/v: the identity u = h(u) implies u = s(x j ) which contradicts \(u\not \in \mathfrak {p}\heartsuit (\mathfrak {m})\). Hence u ≠ h(u) and for the similar reasons, \(v\neq h^{\prime }(v)\);
- if \(u\in \text {loop}_{\overline {\heartsuit }}(s,h)\) :
-
then we proceed in a way similar to the previous case;
- if \(u\in \text {rem}_{\overline {\heartsuit }}(s,h)\) :
-
then we proceed in a way similar to the previous case.
In the remaining cases we have \(u\not \in (\text {dom}(h)\cup \mathfrak {p}\heartsuit (s,h))\). Let us define \(v=\text {maxval}(s^{\prime },h^{\prime })+1\). We have \(v\not \in (\text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (s^{\prime },h^{\prime }))\) and by Proposition 3.16 item 3, we deduce \(u\mathfrak {T} v\). □
Proposition 3.22
Let us assume \({\mathfrak {R}^{\text {\textsf {l}}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) (or equivalently \(\mathfrak {m}\simeq _{b}\mathfrak {m}^{\prime }\)). Then the following statements are equivalent:
Proof
Let us review the easy implications first. Obviously, statement 3 and 4 are equivalent by Theorem 3.17. Then statement 2 implies statement 3 by the two following deductions: \(\mathfrak {R}^{\text {\textsf {l}}}_{1} \subseteq \mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\cap {\mathfrak {T}^{\text {\textsf {l}}}_{2}} \subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\) and \(\mathfrak {R}^{\text {\textsf {l}}}_{2} \subseteq \mathfrak {R}^{\text {\textsf {l}}} \subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}} \cap {\mathfrak {T}^{\text {\textsf {l}}}_{2}} \subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{2}}\).
Let us now show that statement 1 implies statement 2. So we assume \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {D}_{1}}\cap {\mathfrak {D}_{2}}\). We show that \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\), the case \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{2}}\) being treated in a similar way. So let us assume u, v such that \(u\mathfrak {R}^{\text {\textsf {l}}} v\) and let us show that \(u\mathfrak {T}^{\text {\textsf {l}}}_{1} v\). Because \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) we have \(u\mathfrak {T}^{\text {\textsf {l}}} v\). Because \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {D}_{1}}\cap {\mathfrak {D}_{2}}\) we have \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {D}_{1}}\). Let us show that u/v verify (T1–6) with respect to \(\mathfrak {m}_{1}/\mathfrak {m}^{\prime }_{1}\):
- Properties \((\mathfrak {T}\)1,2) hold:
-
because \(u\mathfrak {T}^{\text {\textsf {l}}} v\);
- Property \((\mathfrak {T}3)\)::
-
u = h 1(s(x i )) iff (s(x i ) ∈ dom(h 1) and u = h(s(x i ))) iff (\( s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h_{1}^{\prime })\) and \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\)) iff \(v= h^{\prime }_{1}(s^{\prime }(\mathtt {x}_{i}))\) because \( s(\mathtt {x}_{i})\mathfrak {D}_{1} s^{\prime }(\mathtt {x}_{i})\) (which comes from \( s(\mathtt {x}_{i})\mathfrak {R}^{\text {\textsf {l}}} s^{\prime }(\mathtt {x}_{i})\)) and \(u\mathfrak {T}^{\text {\textsf {l}}} v\);
- Property \((\mathfrak {T}4)\)::
-
u ∈ dom(h 1) iff \(v\in \text {dom}(h_{1}^{\prime })\) because \(u\mathfrak {D}_{1} v\);
- Property \((\mathfrak {T}5)\)::
-
h 1(u) = s(x i ) iff (u ∈ dom(h 1) and h(u) = s(x i )) iff (\(v\in \text {dom}(h_{1}^{\prime })\) and \( h^{\prime }(v)= s^{\prime }(\mathtt {x}_{i})\)) iff \( h^{\prime }_{1}(v)= s^{\prime }(\mathtt {x}_{i})\) because \(u\mathfrak {D}_{1} v\) and \(u\mathfrak {T}^{\text {\textsf {l}}} v\);
- Property \((\mathfrak {T}6)\)::
-
h 1(u) = u iff (u ∈ dom(h 1) and h(u) = u) iff (\(v\in \text {dom}(h_{1}^{\prime })\) and \( h^{\prime }(v)=v\)) iff \( h^{\prime }_{1}(v)=v\) because \(u\mathfrak {D}_{1} v\) and \(u\mathfrak {T}^{\text {\textsf {l}}} v\).
Let us finish by showing that statement 3 implies statement 1. So we assume \(\mathfrak {R}^{\text {\textsf {l}}}_{1}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\) and \(\mathfrak {R}^{\text {\textsf {l}}}_{2}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{2}}\). Let us show theinclusion \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {D}_{1}}\cap {\mathfrak {D}_{2}}\). We assume u, v such that \(u\mathfrak {R}^{\text {\textsf {l}}} v\). Let us show that \(u\mathfrak {D}_{1} v\), the case of \(u\mathfrak {D}_{2} v\) being treated in a similar way. Notice the inclusion \({\mathfrak {T}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {D}_{1}}\) that always holds by Definition 3.14. For \(u\mathfrak {R}^{\text {\textsf {l}}} v\) there are three cases:
-
either u = l and \(v= l^{\prime }\). We have \( l\mathfrak {R}^{\text {\textsf {l}}}_{1} l^{\prime }\), \({\mathfrak {R}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\) and \({\mathfrak {T}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {D}_{1}}\), thus we get \( l\mathfrak {D}_{1} l^{\prime }\) hence \(u\mathfrak {D}_{1}v\);
-
or u = s(x i ) and \(v= s^{\prime }(\mathtt {x}_{i})\) for some i ∈ [1, q]. We have \( s(\mathtt {x}_{i})\mathfrak {R}^{\text {\textsf {l}}}_{1} s^{\prime }(\mathtt {x}_{i})\), \({\mathfrak {R}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {D}_{1}}\), thus we get \(u\mathfrak {D}_{1}v\);
-
or u = h(s(x i )) and \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) for some i ∈ [1, q]. Let usassume u ∈ dom(h 1) and let us prove \(v\in \text {dom}(h_{1}^{\prime })\). From h(s(x i )) ∈ dom(h 1) deduce s(x i ) ∈ dom(h) = dom(h 1) ⊎ dom(h 2). Hence we have two cases:
-
either s(x i ) ∈ dom(h 1). In this case we have h 1(s(x i )) = h(s(x i )) = u ∈ dom(h 1) and s(x i ) ∈ dom(h 1). From \({\mathfrak {R}^{\text {\textsf {l}}}_{1}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{1}}\) we deduce \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}}_{1} s^{\prime }(\mathtt {x}_{i})\) and \( h_{1}(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}}_{1} h^{\prime }_{1}(s^{\prime }(\mathtt {x}_{i}))\). By \((\mathfrak {T}4)\) (twice) we get \( h^{\prime }_{1}(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h_{1}^{\prime })\) and \( s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h_{1}^{\prime })\). We deduce \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= h^{\prime }_{1}(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h_{1}^{\prime })\);
-
or s(x i ) ∈ dom(h 2). In this case we have h 2(s(x i )) = h(s(x i )) = u ∈ dom(h 1) and s(x i ) ∈ dom(h 2). Since dom(h) = dom(h 1) ⊎ dom(h 2) we deduce h(s(x i )) ∈ dom(h) and h 2(s(x i )) ∉ dom(h 2). Because \({\mathfrak {R}^{\text {\textsf {l}}}_{2}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{2}}\) and \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) we have \( s(\mathtt {x}_{i})\mathfrak {T}^{\text {\textsf {l}}}_{2} s^{\prime }(\mathtt {x}_{i})\), \( h(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}} h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\) and \( h_{2}(s(\mathtt {x}_{i}))\mathfrak {T}^{\text {\textsf {l}}}_{2} h^{\prime }_{2}(s^{\prime }(\mathtt {x}_{i}))\). Hence by \((\mathfrak {T}4)\) (three times) we deduce \( s^{\prime }(\mathtt {x}_{i})\in \text {dom}(h_{2}^{\prime })\), \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h^{\prime })\) and \( h^{\prime }_{2}(s^{\prime }(\mathtt {x}_{i}))\not \in \text {dom}(h_{2}^{\prime })\). As a consequence \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= h^{\prime }_{2}(s^{\prime }(\mathtt {x}_{i}))\not \in \text {dom}(h_{2}^{\prime })\) and \(v= h^{\prime }(s^{\prime }(\mathtt {x}_{i}))\in \text {dom}(h^{\prime })\). We conclude \(v\in \text {dom}(h_{1}^{\prime })\).
-
□
Lemma 3.25
Let \(\alpha \geqslant 1\) and let (s, h, l) and \((s^{\prime },h^{\prime },l^{\prime })\) be two pointed memory states. Let \(l_{1}, l_{2}, l^{\prime }_{1}, l^{\prime }_{2}\in \mathbb {N}\) be such that l 1 ∉ dom(h) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\). We assume that one of the conditions below holds:
- (C1) :
-
\( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}1\) – 3), \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}1\) – 6),and l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) ;
- (C2) :
-
\( l_{1}\not \in s (\mathcal {V})\), \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\) 1–3), \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\), and l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) .
If
\((s, h, l) \simeq _{\alpha } (s^{\prime }, h^{\prime }, l^{\prime })\)
then

where β = α − 1 if \(l_{1}\in s (\mathcal {V})\), and β = α otherwise.
Proof
We denote  by \({h_{1\rightarrow 2}}\) and
by \({h_{1\rightarrow 2}}\) and  by \({h_{1\rightarrow 2}}^{\prime }\). According to Proposition 3.10, we have to establish
by \({h_{1\rightarrow 2}}^{\prime }\). According to Proposition 3.10, we have to establish
together with β-equipotence constraints (i ∈ [1, q]):
We start with basic Equivalence (B.1). We have to show that for any B ∈ Basic, \((s,h_{1\rightarrow 2})\models _{l} B\) iff \((s^{\prime },h_{1\rightarrow 2}^{\prime })\models _{l^{\prime }} B\). We prove that \((s,h_{1\rightarrow 2})\models _{l} B\) implies \((s^{\prime },h_{1\rightarrow 2}^{\prime })\models _{l^{\prime }} B\). The reverse implication can be established in a symmetric way. Note that all hypotheses are symmetric: when \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\), we have \( l_{1}\not \in s(\mathcal {V})\) iff \( l^{\prime }_{1}\not \in s^{\prime }(\mathcal {V})\). We proceed by a case analysis on B:
- B is x i = x j ::
-
using \((s,h,l)\simeq _{b}(s^{\prime },h^{\prime },l^{\prime })\), we derive \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}={\mathtt {x}_{j}}\) iff (s, h) ⊧ l x i = x j iff \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}={\mathtt {x}_{j}}\) iff \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}={\mathtt {x}_{j}}\);
- B is x i ↪ x j ::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\) and show that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{ l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\). For \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\) we have two cases:
-
h(s(x i )) = s(x j ). We derive \( h^{\prime }(s^{\prime }(\mathtt {x}_{i})) = s^{\prime }(\mathtt {x}_{j})\) (because \((s,h,l)\simeq _{b}(s^{\prime },h^{\prime },l^{\prime })\)) and thus we also have \({h^{\prime }_{1\rightarrow 2}}(s^{\prime }(\mathtt {x}_{i})) = s^{\prime }(\mathtt {x}_{j})\) hence \((s^{\prime },h_{1\rightarrow 2}^{\prime })\) \( \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\);
-
l 1 = s(x i ) and l 2 = s(x j ). Since \( l_{1}/ l^{\prime }_{1}\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\) in both (C1) and (C2), we get \( l^{\prime }_{1}= s^{\prime }(\mathtt {x}_{i})\) and \( l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{j})\) and thus \({h^{\prime }_{1\rightarrow 2}}(s^{\prime }(\mathtt {x}_{i})) = s^{\prime }(\mathtt {x}_{j})\) and finally \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\).
In both cases we obtain \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\);
-
- B is conv(x i , x j )::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\) and prove that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\). From
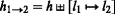 and \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\), we get four cases:
and \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\), we get four cases:
-
s(x i ), s(x j ) ∈ dom(h) and h(s(x i )) = h(s(x j )). Then (s, h) ⊧ l conv(x i , x j ) from which we get \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\) and thus also \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\);
-
h(s(x i )) = l 2 and s(x j ) = l 1. If (C1) holds then \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}3)\) and \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i})) = l^{\prime }_{2}\) and \( s^{\prime }(\mathtt {x}_{j})= l^{\prime }_{1}\). Hence \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\). If (C2) holds then s(x j ) = l 1 contradicts \( l_{1}\not \in s(\mathcal {V})\);
-
the case s(x i ) = l 1 and h(s(x j )) = l 2 is symmetric to the previous one;
-
s(x i ) = s(x j ) = l 1. In case of (C1), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and thus we get \( s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})= l^{\prime }_{1}\) and then \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\). (C2) implies \( l_{1}\not \in s(\mathcal {V})\) which contradicts s(x i ) = l 1.
In all four cases we have \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\);
-
- B is btwn(x i , x j )::
-
let us assume \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\) and prove that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\). We have four cases:
-
h(h(s(x i ))) = s(x j ). Then (s, h) ⊧ l btwn(x i , x j ) from which we get \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\) then \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\);
-
h(s(x i )) = l 1 and l 2 = s(x j ). In both (C1) and (C2), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}3)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\). Hence we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i}))= l^{\prime }_{1}\) and \( l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{j})\). Thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\);
-
l 1 = s(x i ) and h(l 2) = s(x j ). In (C1), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}5)\), hence we get \( l^{\prime }_{1}= s^{\prime }(\mathtt {x}_{i})\) and \( h^{\prime }(l^{\prime }_{2})= s^{\prime }(\mathtt {x}_{j})\), Thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\). In case (C2), l 1 = s(x i ) contradicts \( l_{1}\not \in s(\mathcal {V})\);
-
l 1 = l 2 = s(x i ) = s(x j ). \( l_{1}/ l^{\prime }_{1}\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\) in both (C1) and (C2), hence we get \( l^{\prime }_{1}= l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})\). We deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\).
In all four cases we have \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\);
-
- B is toalloc(x i )::
-
let us assume \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {toalloc}(\mathtt {x}_{i})\) and let us prove \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\). We get four cases:
-
h(s(x i )) ∈ dom(h). Then (s, h) ⊧ l toalloc(x i ) from which we get \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\) then \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\);
-
h(s(x i )) = l 1.\( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}3)\) in both (C1) and (C2), thus we get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i})) = l^{\prime }_{1}\) and thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\);
-
l 1 = s(x i ) and l 2 ∈ dom(h). In case (C1), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}4)\). Then we get \( l^{\prime }_{1}= s^{\prime }(\mathtt {x}_{i})\) and \( l^{\prime }_{2}\in \text {dom}(h^{\prime })\) and we deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\). (C2) implies \( l_{1}\not \in s(\mathcal {V})\) which contradicts s(x i ) = l 1;
-
l 1 = l 2 = s(x i ). \( l_{1}/ l^{\prime }_{1}\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\) in both (C1) and (C2), hence \( l^{\prime }_{1}= l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})\). We deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\).
In all four cases we have \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toalloc}(\mathtt {x}_{i})\);
-
- B is toloop(x i )::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {toloop}(\mathtt {x}_{i})\) and let us prove \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\). We get four cases:
-
h(s(x i )) = h(h(s(x i ))). Then (s, h) ⊧ l toloop(x i ) from which we get \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\) then \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\);
-
h(s(x i )) = l 1 = l 2. In both (C1) and (C2), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}3)\), and l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\). We get \( h^{\prime }(s^{\prime }(\mathtt {x}_{i})) = l^{\prime }_{1}\) and \( l^{\prime }_{1} = l^{\prime }_{2} \) and thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\);
-
l 1 = s(x i ) and h(l 2) = l 2. In case (C1), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}6)\), hence we get \( l^{\prime }_{1}= s^{\prime }(\mathtt {x}_{i})\) and \( h^{\prime }(l^{\prime }_{2}) = l^{\prime }_{2}\) and then \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\). In case (C2), l 1 = s(x i ) contradicts \( l_{1}\not \in s(\mathcal {V})\);
-
l 1 = l 2 = s(x i ). \( l_{1}/ l^{\prime }_{1}\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\) in both (C1) and (C2), hence \( l^{\prime }_{1}= l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{i})= s^{\prime }(\mathtt {x}_{j})\). We deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\).
In all four cases we have \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {toloop}(\mathtt {x}_{i})\);
-
- B is u ↪ u::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {u}\hookrightarrow \mathtt {u}\) and let us prove that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow \mathtt {u}\). We get two cases.
-
h(l) = l. We derive (s, h) ⊧ l u ↪ u then \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow \mathtt {u}\) and hence \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow \mathtt {u}\);
-
l = l 1 = l 2. \( l_{1}/ l^{\prime }_{1}\) verify \(\mathfrak {T}1\), and l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) holds in both (C1) and (C2). Hence we get \( l^{\prime }= l^{\prime }_{1}\) and \( l^{\prime }_{1}= l^{\prime }_{2}\) and thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow \mathtt {u}\).
In both cases we obtain \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow \mathtt {u}\);
-
- B is alloc(u)::
-
let us assume \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {alloc}(\mathtt {u})\) and let us prove that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\). We get two cases.
-
l ∈ dom(h). We derive (s, h) ⊧ l alloc(u) then \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\) and hence \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\);
-
l = l 1. \( l_{1}/ l^{\prime }_{1}\) verify \(\mathfrak {T}1\) in both (C1) and (C2), hence we get \( l^{\prime }= l^{\prime }_{1}\). We deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\).
In both cases we obtain \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {alloc}(\mathtt {u})\);
-
- B is x i = u::
-
using \((s,h,l)\simeq _{b}(s^{\prime },h^{\prime },l^{\prime })\), we derive the equivalences \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}=\mathtt {u}\) iff (s, h) ⊧ l x i = u iff \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}=\mathtt {u}\) iff \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}=\mathtt {u}\);
- B is i ↪ u::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\) and let us prove that \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{ l^{\prime }} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\). We get two cases.
-
h(s(x i )) = l. We derive (s, h) ⊧ l x i ↪ u then \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\) and hence \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\);
-
l 1 = s(x i ) and l 2 = l. In case (C1), \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and \( l_{2}/ l^{\prime }_{2}\) verify \(\mathfrak {T}1\), hence we get \( l^{\prime }_{1}= s^{\prime }(\mathtt {x}_{i})\) and \( l^{\prime }_{2}= l^{\prime }\) and thus \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\). In case (C2), l 1 = s(x i ) contradicts \( l_{1}\not \in s(\mathcal {V})\).
In both cases we obtain \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {x}_{i}\hookrightarrow \mathtt {u}\);
-
- B is u ↪ x j ::
-
let us suppose \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\) and let us show \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\). We get two cases.
-
h(l) = s(x j ). We derive (s, h) ⊧ l u ↪ x j then \((s^{\prime },h^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\) and hence \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\);
-
l 1 = l and l 2 = s(x i ). \( l_{1}/ l^{\prime }_{1}\) verify \(\mathfrak {T}1\)and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\) in both (C1) and (C2), hence we get \( l^{\prime }_{1}= l^{\prime }\) and \( l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{i})\). We deduce \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\).
In both cases we obtain \((s^{\prime },h_{1\rightarrow 2}^{\prime }) \models _{l^{\prime }} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\).
-
This ends the proof of the basic equivalence \((s,h_{1\rightarrow 2},l)\simeq _{b}(s^{\prime },h_{1\rightarrow 2}^{\prime },l^{\prime })\).
Let us consider β-Equipotence (B.2a). By Proposition 2.11, there are three cases for \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\):
- if \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\) and l 2 = s(x i ):
-
then the identity
$$\text{pred}_{\overline{\heartsuit}}(s,h_{1\rightarrow2},i)=\text{pred}_{\overline{\heartsuit}}(s,h,i)\uplus\{ l_{1}\}$$holds. We can treat the case of (C1) and (C2) simulaneously. As \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\)2–3), \( l_{1}/ l^{\prime }_{1}\) also verify \((\mathfrak {T}12)\) and we deduce \( l^{\prime }_{1}\not \in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\). As \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\), we get \( l^{\prime }_{2}= s^{\prime }(\mathtt {x}_{i})\). Thus by Proposition 2.11 again, we have
$$\text{pred}_{\overline{\heartsuit}}(s^{\prime},h_{1\rightarrow2}^{\prime},i) =\text{pred}_{\overline{\heartsuit}}(s^{\prime},h^{\prime},i)\uplus\{ l^{\prime}_{1}\}.$$From \((s,h,l)\simeq _{\alpha }(s^{\prime },h^{\prime },l)\), we have \(\text {pred}_{\overline {\heartsuit }}(s,h,i)\sim _{\alpha }\text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },i)\) by Proposition 2.11 and we derive Equipotence (B.2a) using Lemma 2.19 and \(\beta \leqslant \alpha + 1\);
- if \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {pred}_{\overline {\heartsuit }}(s,h,i)\) :
-
then the identity
$$\text{pred}_{\overline{\heartsuit}}(s,h_{1\rightarrow2},i)= \text{pred}_{\overline{\heartsuit}}(s,h,i)-\{ l_{2}\}$$holds. We treat the case (C1) and (C2) separately.
On the one hand, if (C1) holds then, \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\) and thus also \((\mathfrak {T}10)\). Thus we get \( l^{\prime }_{1}\in s^{\prime }(\mathcal {V})\). Moreover, \( l_{2}/ l^{\prime }_{2}\) verify (\(\mathfrak {T}\)1–6) and thus also \((\mathfrak {T}18)\). Thus we get \( l^{\prime }_{2}\in \text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },i)\). We deduce
$$\text{pred}_{\overline{\heartsuit}}(s^{\prime},h_{1\rightarrow2}^{\prime},i)= \text{pred}_{\overline{\heartsuit}}(s^{\prime},h^{\prime},i)-\{ l^{\prime}_{2}\}$$by Proposition 2.11. Since \( l_{1}\in s(\mathcal {V})\), we have β + 1 = α. Thus by Proposition 2.20, we obtain Equipotence (B.2a);
On the other hand, (C2) contradicts \( l_{1}\in s(\mathcal {V})\);
- in the otherwise case:
-
we have
$$\left( l_{1}\in\mathfrak{p}\heartsuit(s,h)\text{ or } l_{2}\neq s(\mathtt{x}_{i})\right)\text{ and } \left( l_{1}\not\in s(\mathcal{V})\text{ or } l_{2}\not\in\text{pred}_{\overline{\heartsuit}}(s,h,i)\right)$$and \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},i)= \text {pred}_{\overline {\heartsuit }}(s,h,i)\). By a combination of the arguments of two previous cases, in both (C1) and (C2), we have
$$\left( l^{\prime}_{1}\in\mathfrak{p}\heartsuit(s^{\prime}, h^{\prime})\text{ or } l^{\prime}_{2}\neq s^{\prime}(\mathtt{x}_{i})\right)\text{ and } \left( l^{\prime}_{1}\not\in s^{\prime}(\mathcal{V})\text{ or } l^{\prime}_{2}\not\in\text{pred}_{\overline{\heartsuit}}(s^{\prime},h^{\prime},i)\right)$$and thus we get \(\text {pred}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime },i)= \text {pred}_{\overline {\heartsuit }}(s^{\prime },h^{\prime },i)\)by Proposition 2.11. Equipotence (B.2a)is immediate.
Let us consider β-Equipotence (B.2b). We have \(\text {loop}_{\overline {\heartsuit }}(s,h)\sim _{\alpha }\text {loop}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\). By Proposition 2.11, there are three cases for the value of \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\):
- if \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\) and l 1 = l 2 :
-
then \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {loop}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\). As \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}12)\), and l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\), we deduce \( l^{\prime }_{1}\not \in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\) and \( l^{\prime }_{1}= l^{\prime }_{2}\). Thus by Proposition 2.11, we have \(\text {loop}_{\overline {\heartsuit }}(s^{\prime }, h_{1\rightarrow 2}^{\prime })=\text {loop}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\uplus \{ l^{\prime }_{1}\}\). Since we have \(\text {loop}_{\overline {\heartsuit }}(s,h)\sim _{\alpha }\text {loop}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\), we deduce Equipotence (B.2b) using Lemma 2.19 and \(\beta \leqslant \alpha +1\);
- if \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {loop}_{\overline {\heartsuit }}(s,h)\) :
-
then \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})= \text {loop}_{\overline {\heartsuit }}(s,h)-\{ l_{2}\}\).
On the one hand, if (C1) holds then \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}10)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}19)\). Hence we get \( l^{\prime }_{1}\in s^{\prime }(\mathcal {V})\) and \( l^{\prime }_{2}\in \text {loop}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\). We deduce \(\text {loop}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime })= \text {loop}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })-\{ l^{\prime }_{2}\}\). Since \( l_{1}\in s(\mathcal {V})\), we have β + 1 = α and thus by Proposition 2.20 we get Equipotence (B.2b).
On the other hand, (C2) contradicts \( l_{1}\in s(\mathcal {V})\);
- in the otherwise case:
-
we have
$$\left( l_{1}\in\mathfrak{p}\heartsuit(s,h)\text{ or } l_{1}\neq l_{2}\right)\text{ and } \left( l_{1}\not\in s(\mathcal{V})\text{ or } l_{2}\not\in\text{loop}_{\overline{\heartsuit}}(s,h)\right)$$and \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {loop}_{\overline {\heartsuit }}(s,h)\). By a combination of the arguments of two previous cases, in both (C1) and (C2), we have
$$\left( l^{\prime}_{1}\in\mathfrak{p}\heartsuit(s^{\prime}, h^{\prime})\text{ or } l^{\prime}_{1}\neq l^{\prime}_{2}\right)\text{ and } \left( l^{\prime}_{1}\not\in s^{\prime}(\mathcal{V})\text{ or } l^{\prime}_{2}\not\in\text{loop}_{\overline{\heartsuit}}(s^{\prime},h^{\prime})\right)$$thus \(\text {loop}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime })=\text {loop}_{\overline {\heartsuit }} (s^{\prime },h^{\prime })\). Equipotence (B.2b) is immediate.
Let us consider β-Equipotence (B.2c). We have \(\text {rem}_{\overline {\heartsuit }}(s,h)\sim _{\alpha }\text {rem}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\). By Proposition 2.11, there are three cases for the value of \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\):
- if \( l_{1}\not \in \mathfrak {p}\heartsuit (s,h)\cup \{ l_{2}\}\) and \( l_{2}\not \in s(\mathcal {V})\) :
-
then \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {rem}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\). As \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}12)\), l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\), and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}10)\), we deduce \( l^{\prime }_{1}\not \in \mathfrak {p}\heartsuit (s^{\prime }, h^{\prime })\), \( l^{\prime }_{1}\neq l^{\prime }_{2}\) and \( l^{\prime }_{2}\not \in s^{\prime }(\mathcal {V})\). Thus by Proposition 2.11, we have \(\text {rem}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime })= \text {rem}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\uplus \{ l^{\prime }_{1}\}\). Since we have \(\text {rem}_{\overline {\heartsuit }}(s,h)\sim _{\alpha }\text {rem}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\), we deduce Equipotence (B.2c) using Lemma 2.19 and \(\beta \leqslant \alpha +1\);
- if \( l_{1}\in s(\mathcal {V})\) and \( l_{2}\in \text {rem}_{\overline {\heartsuit }}(s,h)\) :
-
then \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})= \text {rem}_{\overline {\heartsuit }}(s,h)-\{ l_{2}\}\).
On the one hand, if Hypothesis (C1) holds then\( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}10)\) and \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}20)\). Hence we get \( l^{\prime }_{1}\in s^{\prime }(\mathcal {V})\) and \( l^{\prime }_{2}\in \text {rem}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })\). We deduce \(\text {rem}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime })= \text {rem}_{\overline {\heartsuit }}(s^{\prime },h^{\prime })-\{ l^{\prime }_{2}\}\). Since \( l_{1}\in s(\mathcal {V})\), we have β + 1 = α and thus by Proposition 2.20 we get Equipotence (B.2c).
On the other hand, (C2) contradicts \( l_{1}\in s(\mathcal {V})\);
- in the otherwise case:
-
we have
$$\left( l_{1}\in\mathfrak{p}\heartsuit(s,h)\cup\{ l_{2}\}\text{ or } l_{2}\in s(\mathcal{V})\right)\text{ and } \left( l_{1}\not\in s(\mathcal{V})\text{ or } l_{2}\not\in\text{rem}_{\overline{\heartsuit}}(s,h)\right)$$and \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {rem}_{\overline {\heartsuit }}(s,h)\). By a combination of the arguments of two previous cases, in both (C1) and (C2), we have
$$\left( l^{\prime}_{1}\in\mathfrak{p}\heartsuit(s^{\prime}, h^{\prime})\cup\{ l^{\prime}_{2}\}\text{ or } l^{\prime}_{2}\in s^{\prime}(\mathcal{V})\right)\text{ and } \left( l^{\prime}_{1}\not\in s^{\prime}(\mathcal{V})\text{ or } l^{\prime}_{2}\not\in\text{rem}_{\overline{\heartsuit}}(s^{\prime},h^{\prime})\right)$$thus \(\text {rem}_{\overline {\heartsuit }}(s^{\prime },h_{1\rightarrow 2}^{\prime })=\text {rem}_{\overline {\heartsuit }} (s^{\prime },h^{\prime })\). Equipotence (B.2c) is immediate.
□
Proposition 3.26
Let
\(\mathfrak {m} =(s,h,l)\)
be a pointed
memory state and
\( l_{1}, l_{2}\in \mathbb {N}\)
be
such that
\(l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\). We have
 . Moreover, given \(\alpha \geqslant 0\), if we assume that one of the following conditions hold
. Moreover, given \(\alpha \geqslant 0\), if we assume that one of the following conditions hold
- (C1):
-
l 2 = s(x i ) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s , h ,i))\geqslant \alpha \) for some i ∈ [1, q];
- (C2):
-
l 2 = l 1 and \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))\geqslant \alpha \);
- (C3):
-
\( l_{2}\not \in s (\mathcal {V})\cup \{ l_{1}\}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s, h))\geqslant \alpha \).
then we have  .
.
Proof
We write \({h_{1\rightarrow 2}}\) to denote  . First, without assuming any of (C1–3), let us prove that \((s,h_{1\rightarrow 2},l)\simeq _{b}(s,h,l)\) holds. By Proposition 3.2 (monotonicity), we only need to prove that \((s,h_{1\rightarrow 2}) \models _{l} B\) implies (s, h) ⊧
l
B for any formula B ∈ Basic
u. We proceed by a case analysis on B:
. First, without assuming any of (C1–3), let us prove that \((s,h_{1\rightarrow 2},l)\simeq _{b}(s,h,l)\) holds. By Proposition 3.2 (monotonicity), we only need to prove that \((s,h_{1\rightarrow 2}) \models _{l} B\) implies (s, h) ⊧
l
B for any formula B ∈ Basic
u. We proceed by a case analysis on B:
- B is x i = x j ::
-
This only depends on the value of s and therefore we are done;
- B is x i ↪ x j ::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}}\), we get \({h_{1\rightarrow 2}}(s(\mathtt {x}_{i}))= s(\mathtt {x}_{j})\). But since \( l_{1}\not \in \mathfrak {p}\heartsuit (\mathfrak {m})\), we deduce l 1 s≠ s(x i ) and thus h(s(x i )) = x s( j ). We get (s, h) ⊧ l x i ↪ x j ;
- B is conv(x i , x j )::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{j})\), the identity \({h_{1\rightarrow 2}}(s(\mathtt {x}_{i}))={h_{1\rightarrow 2}}(s(\mathtt {x}_{j}))\) holds. But since l 1 ∉ {s(x i ), s(x j )}, we deduce h(s(x i )) = h(s(x j )) and thus (s, h) ⊧ l conv(x i , x j );
- B is btwn(x i , x j )::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j})\), we get \({h_{1\rightarrow 2}}({h_{1\rightarrow 2}}(s(\mathtt {x}_{i})))=\) s( j ). But since l 1 ∉ {s(x i ), h(s(x i ))} (remember \( h(s(\mathtt {x}_{i}))\in \mathfrak {p}\heartsuit (\mathfrak {m})\)), we get h(h(s(x i ))) = s(x j ) and thus we derive (s, h) ⊧ l btwn(x i , x j );
- B is toalloc(x i )::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {toalloc}(\mathtt {x}_{i})\), we deduce \({h_{1\rightarrow 2}}(s(\mathtt {x}_{i})))\) \(\in \text {dom}(h_{1\rightarrow 2})\). Since l 1 ≠ s( i ), we get \( h(s(\mathtt {x}_{i})))\in \text {dom}(h)\cup \{ l_{1}\}\). Since h(s(x i )) ≠ l 1, we deduce h(s(x i )) ∈ dom(h) and thus (s, h) ⊧ l toalloc(x i );
- B is toloop(x i )::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {toloop}(\mathtt {x}_{i})\) we get \({h_{1\rightarrow 2}}({h_{1\rightarrow 2}}(s(\mathtt {x}_{i})))={h_{1\rightarrow 2}}(s(\mathtt {x}_{i}))\). But since l 1 ∉ {s(x i ), h(s(x i ))}, we get h(h(s(x i ))) = h(s(x i )) and thus (s, h) ⊧ l toloop(x i );
- B is u ↪ u::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {u}\hookrightarrow {\mathtt {u}}\) we get \({h_{1\rightarrow 2}}(l)= l\). But since l 1 ≠ l, we deduce h(l) = l and thus (s, h) ⊧ l u ↪ u;
- B is alloc(u)::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {alloc}(\mathtt {u})\) we get \( l\in \text {dom}(h_{1\rightarrow 2})\). But since l 1 ≠ l and \(\text {dom}(h_{1\rightarrow 2})=\text {dom}(h)\cup \{ l_{1}\}\), we deduce l ∈ dom(h) and thus (s, h) ⊧ l alloc(u);
- B is x i = u::
-
only depends on the values of s and l;
- B is x i ↪ u::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {x}_{i}\hookrightarrow {\mathtt {u}}\) we get \({h_{1\rightarrow 2}}(s(\mathtt {x}_{i}))= l\). Since l 1 ≠ s(x i ), we deduce h(s(x i )) = l and thus (s, h) ⊧ l x i ↪ u;
- B is u ↪ x j ::
-
from \((s,h_{1\rightarrow 2}) \models _{l} \mathtt {u}\hookrightarrow {\mathtt {x}_{j}}\) we get \({h_{1\rightarrow 2}}(l)= s(\mathtt {x}_{i})\).But since l 1≠l,we deduce h(l) = s( i )and thus (s, h)⊧ l ↪ j .
Now we assume α ≥ 0 such that one of either (C1), (C2) or (C3) holds. Since we already have \((s,h_{1\rightarrow 2},l)\simeq _{b}(s,h,l)\), according to Proposition 3.10, we have to establish three α-equipotence constraints:
If (C1) holds then by Proposition 2.11, we have the equations \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)=\text {pred}_{\overline {\heartsuit }}(s,h,j)\uplus \{ l_{1}\}\) if s(x i ) = s(x j ), \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)=\text {pred}_{\overline {\heartsuit }}(s,h,j)\)if s(x i ) ≠ s(x j ), \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {loop}_{\overline {\heartsuit }}(s,h)\) and \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {rem}_{\overline {\heartsuit }}(s,h)\). Then we already have \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)\sim _{\alpha }\text {pred}_{\overline {\heartsuit }}(s,h,j)\) when s(x i ) ≠ s(x j ), \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\sim _{\alpha }\text {loop}_{\overline {\heartsuit }}(s,h)\) and \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})\sim _{\alpha }\text {rem}_{\overline {\heartsuit }}(s,h)\). If s(x i ) = s(x j ) holds then wehave \(\text {pred}_{\overline {\heartsuit }}(s,h,j)=\text {pred}_{\overline {\heartsuit }}(s,h,i)\). As a consequence, we get \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j))\geqslant \alpha +1\) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))\geqslant \alpha \). Hence \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)\sim _{\alpha }\text {pred}_{\overline {\heartsuit }}(s,h,j)\) holds as well.
If (C2) holds then by Proposition 2.11, we have \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)=\text {pred}_{\overline {\heartsuit }}(s,h,j)\). Indeed, l 2 = s(x j ) implies \( l_{1}= l_{2}\in s(\mathcal {V})\) which contradicts \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\). We also get \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {loop}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\) and \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {rem}_{\overline {\heartsuit }}(s,h)\). The three α-equipotence constraints follow.
If (C3) holds then by Proposition 2.11, we have \(\text {pred}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2},j)=\text {pred}_{\overline {\heartsuit }}(s,h,j)\), \(\text {loop}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {loop}_{\overline {\heartsuit }}(s,h)\) and \(\text {rem}_{\overline {\heartsuit }}(s,h_{1\rightarrow 2})=\text {rem}_{\overline {\heartsuit }}(s,h)\uplus \{ l_{1}\}\). The α-equipotence constraints follow. □
Corollary 3.27
Let \(\alpha \geqslant 0\). Let \(\mathfrak {m} =(s,h,l)\) be a pointed memory state and \( h^{\prime }\) be a heap such that \(\text {dom}(h^{\prime })\cap (\text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m}))=\varnothing \). If for any \(u\in \text {dom}(h^{\prime })\) one of the following conditions holds
- (C1) :
-
\( h^{\prime }(u)= s (\mathtt {x}_{i})\) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s , h ,i))\geqslant \alpha \) for some i ∈ [1, q];
- (C2) :
-
\( h^{\prime }(u)=u\) and \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s, h))\geqslant \alpha \) ;
- (C3) :
-
\( h^{\prime }(u)\not \in s (\mathcal {V})\cup \{u\}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s, h))\geqslant \alpha \).
then we have
 .
.
Proof
We prove the result by induction on (the size of the domain of) \( h^{\prime }\). If \( h^{\prime }=\Box \) then the result it trivial by reflexivity of ≃
α
. Otherwise, we can write  . From \(\text {dom}(h^{\prime })\cap (\text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m}))=\varnothing \) we deduce \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\). We apply Proposition 3.26 to \(\mathfrak {m}\), l
1 and l
2 and we get
. From \(\text {dom}(h^{\prime })\cap (\text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m}))=\varnothing \) we deduce \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\). We apply Proposition 3.26 to \(\mathfrak {m}\), l
1 and l
2 and we get  .
.
We then use the induction hypothesis on \( h^{\prime \prime }\) (with  replacing h). Let us verify the requirements:
replacing h). Let us verify the requirements:
-
We have \(\text {dom}(h^{\prime \prime })\cap \)
 \(=\text {dom}(h^{\prime \prime })\cap (\text {dom}(h)\cup \{ l_{1}\}\cup \mathfrak {p}\heartsuit (s,h,l)) =\varnothing \) because \( l_{1}\not \in \text {dom}(h^{\prime \prime })\) and \( l_{1}\not \in s(\mathcal {V})\).
\(=\text {dom}(h^{\prime \prime })\cap (\text {dom}(h)\cup \{ l_{1}\}\cup \mathfrak {p}\heartsuit (s,h,l)) =\varnothing \) because \( l_{1}\not \in \text {dom}(h^{\prime \prime })\) and \( l_{1}\not \in s(\mathcal {V})\). -
Let \(u\in \text {dom}(h^{\prime \prime })\). Let us show that either (C1), (C2) or (C3) holds for u. We have \(u\in \text {dom}(h^{\prime })\) and \( h^{\prime }(u)= h^{\prime \prime }(u)\). By hypothesis, one of the following conditions holds:
-
\( h^{\prime }(u)= s(\mathtt {x}_{i})\) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,i))\geqslant \alpha \) for some i ∈ [1, q]. From \( s(\mathcal {V})\subseteq \mathfrak {p}\heartsuit (s,h,l)\), we deduce \( l_{1}\not \in s(\mathcal {V})\). Thus by Proposition 2.11 we have
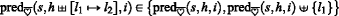
hence
 . We also have \( h^{\prime \prime }(u)= h^{\prime }(u)= s(\mathtt {x}_{i})\) hence Condition (C1) holds;
. We also have \( h^{\prime \prime }(u)= h^{\prime }(u)= s(\mathtt {x}_{i})\) hence Condition (C1) holds; -
\( h^{\prime }(u)= u\) and \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))\geqslant \alpha \). By Proposition 2.11 again, from \( l_{1}\not \in s(\mathcal {V})\) we deduce
 . As \( h^{\prime \prime }(u)= h^{\prime }(u)= u\), Condition (C2) holds;
. As \( h^{\prime \prime }(u)= h^{\prime }(u)= u\), Condition (C2) holds; -
\( h^{\prime }(u)\not \in s(\mathcal {V})\cup \{u\}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h))\geqslant \alpha \). By Proposition 2.11 again, from \( l_{1}\not \in s(\mathcal {V})\) we deduce
 . As \( h^{\prime \prime }(u)= h^{\prime }(u)\not \in s(\mathcal {V})\cup \{u\}\), Condition (C3) holds.
. As \( h^{\prime \prime }(u)= h^{\prime }(u)\not \in s(\mathcal {V})\cup \{u\}\), Condition (C3) holds.
-
As a consequence, we obtain  by induction and thus
by induction and thus  by transitivity of ≃
α
. □
by transitivity of ≃
α
. □
Proposition 3.29
Let \(\alpha \geqslant 1\). We assume that the following conditions hold:
-
(a)
\(\mathfrak {m} \simeq _{\alpha +1}\mathfrak {m}^{\prime }\) ;
-
(b)
\(\mathfrak {m}_{0}\simeq _{\alpha +1}\mathfrak {m}^{\prime }_{0}\) ;
-
(c)
\(\text {dom}(h) \subseteq \mathfrak {p}\heartsuit (\mathfrak {m})\) ;
-
(d)
\(\text {dom}(h^{\prime })\subseteq \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\).
Let
 and \( l_{2}\in \mathbb {N}\). There exist \( l^{\prime }_{1}, l^{\prime }_{2}\in \mathbb {N}\) such that
and \( l_{2}\in \mathbb {N}\). There exist \( l^{\prime }_{1}, l^{\prime }_{2}\in \mathbb {N}\) such that
-
1.
 ;
; -
2.
\(l^{\prime }_{1}, l^{\prime }_{2}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\);
-
3.
 ;
; -
4.
 .
.
Proof
According to Lemma 3.19, we have both \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) and \({\mathfrak {R}^{\text {\textsf {l}}}_{0}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{0}}\).
Let use define \( l^{\prime }_{1}\) to be the unique value such that \( l_{1}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{1}\). We also have \( l_{1}\mathfrak {R}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\). Hence we get both \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) and \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\). From \( l_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m})\) and \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) we deduce \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\). Since \( l_{1}\in s^{\prime }(\mathcal {V})\) and  from \(l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) we deduce
from \(l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) we deduce  by \((\mathfrak {T}10)\) and \((\mathfrak {T}4)\). Hence Property 1 holds.
by \((\mathfrak {T}10)\) and \((\mathfrak {T}4)\). Hence Property 1 holds.
Let us define \( l^{\prime }_{2}\) by Proposition 3.20: since α ≥ 1, we have \(\mathfrak {m}_{0} \simeq _{2}\mathfrak {m}^{\prime }_{0}\), and thus there exists \( l^{\prime }_{2}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\) such that \( l_{2}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\). Property 2 holds because \( l^{\prime }_{1}\in s^{\prime }(\mathcal {V})\) and \( l^{\prime }_{2}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\).
Let us establish Property 4, i.e.  . We use Lemma 3.25 (C1) with \(\mathfrak {m}_{0}/\mathfrak {m}^{\prime }_{0}\). We have both
. We use Lemma 3.25 (C1) with \(\mathfrak {m}_{0}/\mathfrak {m}^{\prime }_{0}\). We have both  and
and  . \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\)1–3) because \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) holds. \( l_{2}/ l^{\prime }_{2}\) verify (\(\mathfrak {T}\)1–6) because \( l_{2}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\) holds. Letus check l
1 = l
2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\):
. \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\)1–3) because \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) holds. \( l_{2}/ l^{\prime }_{2}\) verify (\(\mathfrak {T}\)1–6) because \( l_{2}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\) holds. Letus check l
1 = l
2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\):
-
if \( l_{2}\in \mathfrak {p}\heartsuit (\mathfrak {m}_{0})\) then \( l_{2}\mathfrak {R}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\) by Proposition 3.15 item 5. Since \( l_{1}\mathfrak {R}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\), \( l_{2}\mathfrak {R}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\) and \(\mathfrak {R}^{\text {\textsf {l}}}_{0}\) is a bijection (Lemma 3.19), we deduce l 1 = l 2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\);
-
if \( l_{2}\not \in \mathfrak {p}\heartsuit (\mathfrak {m}_{0})\) then \(l^{\prime }_{2}\not \in \mathfrak {p}\heartsuit (\mathfrak {m}_{0}^{\prime })\) by \((\mathfrak {T}21)\) with \( l_{2}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\). But \( l_{1}\in s(\mathcal {V})\) and \( l^{\prime }_{1}\in s^{\prime }(\mathcal {V})\) hence l 1 ≠ l 2 and \( l^{\prime }_{1}\neq l^{\prime }_{2}\) and we deduce l 1 = l 2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\).
We apply Lemma 3.25 (C1) with Hypothesis (b) and we get Property 4.
Let us show Property 3, i.e.  . We use Lemma 3.25 (C1) with \(\mathfrak {m}/\mathfrak {m}^{\prime }\). Since
. We use Lemma 3.25 (C1) with \(\mathfrak {m}/\mathfrak {m}^{\prime }\). Since  and
and  then l
1 ∉ dom(h) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\). \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\)1–3) because \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) holds. We already verified that l
1 = l
2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\) holds. Letus check that \( l_{2}/ l^{\prime }_{2}\) verify (\(\mathfrak {T}\)1–6), i.e. \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\):
then l
1 ∉ dom(h) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\). \( l_{1}/ l^{\prime }_{1}\) verify (\(\mathfrak {T}\)1–3) because \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) holds. We already verified that l
1 = l
2 iff \( l^{\prime }_{1}= l^{\prime }_{2}\) holds. Letus check that \( l_{2}/ l^{\prime }_{2}\) verify (\(\mathfrak {T}\)1–6), i.e. \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\):
-
if \( l_{2}\in \mathfrak {p}\heartsuit (\mathfrak {m})\) then, as \( l_{2}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{2}\) holds, by Proposition 3.28, we get \( l_{2}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{2}\) and thus \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\);
-
if \( l_{2}\not \in \mathfrak {p}\heartsuit (\mathfrak {m})\) then we must have \( l^{\prime }_{2}\not \in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\): otherwise if \( l^{\prime }_{2}\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) holds then we would have \( l_{2}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{2}\) by Proposition 3.28, which contradicts \( l_{2}\not \in \mathfrak {p}\heartsuit (\mathfrak {m})\). Hence by Hypotheses (c) and (d) we deduce l 2 ∉ dom(h) and \( l^{\prime }_{2}\not \in \text {dom}(h^{\prime })\). By Proposition 3.16 item 4, we deduce \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\).
We apply Lemma 3.25 (C1) with Hypothesis (a) and we get Property 3. □
Proposition 3.31
Let \(\alpha \geqslant 1\). We assume that the following conditions hold:
-
(a)
\(\mathfrak {m} \simeq _{\alpha }\mathfrak {m}^{\prime }\) ;
-
(b)
\(\mathfrak {m}_{0}\simeq _{\alpha }\mathfrak {m}^{\prime }_{0}\).
Let
 and \(l_{2}\in \mathbb {N}\). There exist \( l^{\prime }_{1}, l^{\prime }_{2}\in \mathbb {N}\) such that
and \(l_{2}\in \mathbb {N}\). There exist \( l^{\prime }_{1}, l^{\prime }_{2}\in \mathbb {N}\) such that
-
1.

-
2.
\(l^{\prime }_{1}, l^{\prime }_{2}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+2\);
-
3.
 ;
; -
4.
 .
.
Proof
According to Lemma 3.19, we have both \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) and \({\mathfrak {R}^{\text {\textsf {l}}}_{0}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}_{0}}\).
Let us define \( l^{\prime }_{1}\) and simultaneously check Property 1 and prove that \( l^{\prime }_{1}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\), \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) and \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) hold:
-
if \( l_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}_{0})\) then let us define \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}_{0}^{\prime })\) as the unique value such that \( l_{1}\mathfrak {R}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\). We immediately deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\). As a consequence,
 by \((\mathfrak {T}4)\)and \( l^{\prime }_{1}\not \in s^{\prime }(\mathcal {V})\) by \((\mathfrak {T}10)\). Hence Property 1 holds. As \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}_{0}^{\prime })\), the relation \( l^{\prime }_{1}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\) holds trivially. Only \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) remains. We use Proposition 3.28: if \( l_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m})\) or \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) then \( l_{1}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{1}\), hence \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\); otherwise both \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) hold and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) by Proposition 3.16 item 4;
by \((\mathfrak {T}4)\)and \( l^{\prime }_{1}\not \in s^{\prime }(\mathcal {V})\) by \((\mathfrak {T}10)\). Hence Property 1 holds. As \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}_{0}^{\prime })\), the relation \( l^{\prime }_{1}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\) holds trivially. Only \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) remains. We use Proposition 3.28: if \( l_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m})\) or \( l^{\prime }_{1}\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) then \( l_{1}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{1}\), hence \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\); otherwise both \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) hold and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) by Proposition 3.16 item 4; -
if \( l_{1}\not \in \mathfrak {p}\heartsuit (\mathfrak {m}_{0})\) then we define \(l^{\prime }_{1}=\text {maxval}(\mathfrak {m}^{\prime }_{0})+1\) and Property 1 holds in an obvious way. We also have
 and
and  and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) by Proposition 3.16 item 4. A fortiori we have \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) by Proposition 3.16 item 4.
and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) by Proposition 3.16 item 4. A fortiori we have \( l_{1}\not \in \text {dom}(h)\cup \mathfrak {p}\heartsuit (\mathfrak {m})\) and \( l^{\prime }_{1}\not \in \text {dom}(h^{\prime })\cup \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\) and we deduce \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) by Proposition 3.16 item 4.
From \( l^{\prime }_{1}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\), we obviously derive Property 2 for \( l^{\prime }_{1}\).
Let us define \( l^{\prime }_{2}\) by choosing the first possible choice in the following list. We simultaneously check Property 2 for \( l_{2}^{\prime }\) and prove that \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\), and that l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) holds:
-
if l 2 = l 1 then we define \( l^{\prime }_{2}= l^{\prime }_{1}\). In case, Property 2 obviously holds for \( l^{\prime }_{2}\) since it holds for \( l^{\prime }_{1}\). Since \( l_{1}\mathfrak {T}^{\text {\textsf {l}}}_{0} l^{\prime }_{1}\) holds then \( l_{1}/ l^{\prime }_{1}\) verify \((\mathfrak {T}2)\), and thus \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\). Since l 2 = l 1 and \( l^{\prime }_{2}= l^{\prime }_{1}\), the property l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) holds;
-
if \( l_{2}\in s(\mathcal {V})\) then we define \( l^{\prime }_{2}\) to be the unique location such that \( l_{2}\mathfrak {R}^{\text {\textsf {l}}} l^{\prime }_{2}\). Then \( l^{\prime }_{2}\in \mathfrak {p}\heartsuit (\mathfrak {m}^{\prime })\subseteq \mathfrak {p} \heartsuit (\mathfrak {m}_{0}^{\prime })\) and as a consequence, Property 2 holds for \( l_{2}^{\prime }\). From \(\mathfrak {R}^{\text {\textsf {l}}}\subseteq {\mathfrak {T}^{\text {\textsf {l}}}}\) we deduce \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\) and as a consequence, \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\). We have \( l_{1}\not \in s(\mathcal {V})\) hence we deduce \( l^{\prime }_{1}\not \in s^{\prime }(\mathcal {V})\) using \( l_{1}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{1}\) and \((\mathfrak {T}10)\). We have \( l_{2}\in s(\mathcal {V})\) hence we deduce \( l^{\prime }_{2}\in s^{\prime }(\mathcal {V})\) using \( l_{2}\mathfrak {T}^{\text {\textsf {l}}} l^{\prime }_{2}\) and \((\mathfrak {T}10)\). We derive both l 1 ≠ l 2 and \( l^{\prime }_{1}\neq l^{\prime }_{2}\). Thus the property l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\)holds;
-
otherwise we have \( l_{2}\not \in s(\mathcal {V})\) and l 1 ≠ l 2 an we define \( l^{\prime }_{2}=\text {maxval}(\mathfrak {m}^{\prime }_{0})+2\). Hence Property 2 holds for \( l_{2}^{\prime }\). Moreover, as \( l^{\prime }_{1}\leqslant \text {maxval}(\mathfrak {m}^{\prime }_{0})+1\), we deduce \( l^{\prime }_{1}\neq l^{\prime }_{2}\). Thus the property l 2 = l 1 iff \( l^{\prime }_{2}= l^{\prime }_{1}\) holds. Finally we have \( l_{2}\not \in s(\mathcal {V})\) and \( l^{\prime }_{2}\not \in s^{\prime }(\mathcal {V})\) (because \( l^{\prime }_{2}>\text {maxval}(\mathfrak {p}\heartsuit (\mathfrak {m}_{0}^{\prime }))\)). Hence \( l_{2}/ l^{\prime }_{2}\) verify \((\mathfrak {T}2)\).
We apply Lemma 3.25 (C2) with Hypothesis (a) and (b) and we get Property 3 and 4. □
Appendix C: Proofs of Section 4
Corollary 4.14
1SL2 is strictly more expressive than 1SL1.
Proof
Let A be the sentence in 1SL2 that states that there is a path of length 3 between x 1 and x 2 in the memory state and nothing else, for instance
with
Suppose that there is a sentence \( A^{\prime }\) in 1SL1 whose models are precisely the memory states defined by A. Let us show that this leads to a contradiction.
Let \(q \geqslant 1\) be such that x 1,…, x q contains the program variables that occur in \( A^{\prime }\). By Theorem 4.11, there is a Boolean combination \( A^{\prime \prime }\) of test formulae from \(\text {\textsf {Test}}_{\alpha }^{\mathtt {u}}\) such that \( A^{\prime }\) and \( A^{\prime \prime }\) are equivalent, where \(\alpha = \text {\textsf {th}}(q, A^{\prime })\). Let s be the store with s(x 1) = 0 and s(x 2) = 3. Let h 1 be the heapsuch that h 1(0) = 1, h 1(1) = 2 and h 1(2) = 3. Similarly, let h 2 be the heap such that h 2(0) = 1, h 2(1) = 2 and h 2(4) = 3. And let l = 0 for instance (any other value would fit). We note that (s, h 1) ⊧ l A and therefore \((s,h_{1}) \models _{l} A^{\prime }\) by assumption. Similarly, \((s,h_{2}) \nvDash _{l} A\) and therefore \((s,h_{2}) \nvDash _{l} A^{\prime }\) by assumption.
Since \( A^{\prime }\) and \( A^{\prime \prime }\) are two logically equivalent formulæ of 1SL1, we deduce that both \((s,h_{1}) \models _{l} A^{\prime \prime }\) and \((s,h_{2}) \nvDash _{l} A^{\prime \prime }\) hold. However, it is worth noting that for every test formula B from \(\text {\textsf {Test}}_{\alpha }^{\mathtt {u}}\), we have (s, h 1) ⊧ l B iff (s, h 2) ⊧ l B, which leads to a contradiction because \( A^{\prime \prime }\) is a Boolean combination of formulae from \(\text {\textsf {Test}}_{\alpha }^{\mathtt {u}}\). □
Lemma 4.15
Let \(q\geqslant 1\) and \(m\in \mathbb {N}\). Let A be a 1SL1 formula with program variables in x 1,…, x q and (s, h, l) be a pointed memory state. If we assume \(\text {maxval}(s,h,l)+\varphi _{q}(A )\leqslant m\) then
Proof
We proceed by induction on A and we prove the double implication, assuming that \(\text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\)holds:
- if A is atomic:
-
then bmc(q, m, A, (s, h, l)) = amc(A, (s, h, l)). The correctness of is amc obvious and left to the reader;
- if A is ¬A 1 :
-
then
$$\mathtt{bmc}(q,m,A,(s ,h ,l))=\mathtt{not}\ \mathtt{bmc}(q,m,A_{1},(s ,h ,l)).$$We deduce the equivalences bmc(q, m, A, (s, h, l)) = tt iff bmc(q, m, A 1, (s, h, l)) ≠ tt iff\((s,h)\nvDash _{l} A_{1}\)iff (s, h) ⊧ l A using the induction hypothesis;
- if A is A 1 ∧ A 2 :
-
then
$$\mathtt{bmc}(q,m,A,(s ,h ,l))= \mathtt{bmc}(q,m,A_{1},(s ,h ,l))\ \mathtt{ and }\ \mathtt{bmc}(q,m,A_{2},(s ,h ,l)).$$We deduce bmc(q, m, A, (s, h, l)) = tt iff bmc(q, m, A 1, (s, h, l)) = tt and bmc(q, m, A 2, (s, h, l)) = tt iff (s, h) ⊧ l A 1 and (s, h) ⊧ l A 2 iff (s, h) ⊧ l A using the induction hypotheses;
- if A is ∃u A 1,:
-
let us assume bmc(q, m, ∃u A 1, (s, h, l)) tt = and prove (s, h) ⊧ l ∃u A 1. By definition, there exists \(l_{0}\leqslant m\) such that \(l_{0}+\varphi _q(A_{1})\leqslant m\) and bmc(q, m, A 1, (s, h, l 0)) = tt. We have \(\text {maxval}(s,h)+\varphi _q(A_{1})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 1. Hence we deduce \(\text {maxval}(s,h,l_{0})+\varphi _q(A_{1})\leqslant m\). By induction hypothesis we get \((s,h)\models _{l_{0}} A_{1}\) and thus (s, h) ⊧ l ∃u A 1.
Now let us assume (s, h) ⊧ l ∃u A 1 and prove bmc(q, m, ∃u A 1, (s, h, l)) = tt. By Corollary 4.5, there exists \(l_{0}\leqslant \text {maxval}(s,h)+1\) s.t. \((s,h)\models _{l_{0}} A_{1}\). We have \(\text {maxval}(s,h)+1+\varphi _q(A_{1})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 1. Hence we get both \(l_{0}+\varphi _q(A_{1})\leqslant m\) and \(\text {maxval}(s,h)+\varphi _q(A_{1})\leqslant m\) and we deduce \(\text {maxval}(s,h,l_{0})+\varphi _q(A_{1})\leqslant m\). We get bmc(q, m, A 1, (s, h, l 0)) = tt by induction. By definition of bmc, we conclude (q, m, ∃u A 1, (s, h, l)) = tt;
- if A is A 1 ∗ A 2,:
-
let us assume bmc(q, m, A 1 ∗ A 2, (s, h, l 0)) = tt and let us prove (s, h) ⊧ l A 1 ∗ A 2. By definition of bmc, there exists a heap \(h_{1}:[0,m]\rightharpoondown [0,m]\) such that \(\text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) and \(h_{1}\sqsubseteq h\) and bmc(q, m, A 1, (s, h, l)) = tt and bmc(q, m, A 2, (s, h, l)) = tt with h 2 = h − h 1. For each c ∈ {1, 2}, we have \(\text {maxval}(s,h_{c},l)+\varphi _q(A_{c})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 4. Hence by induction hypotheses, we deduce (s, h 1) ⊧ l A 1 and (s, h 2) ⊧ l A 2. Given that the identity
 holds, we get (s, h) ⊧
l
A
1 ∗ A
2.
holds, we get (s, h) ⊧
l
A
1 ∗ A
2.Now let us assume (s, h) ⊧ l A 1 ∗ A 2 and prove bmc(q, m, A 1 ∗ A 2, (s, h, l 0)) = tt. There exist h 1 and h 2 such that
 and (s, h
2) ⊧
l
A
2. For each c ∈ {1, 2}, from \(h_{c}\sqsubseteq h\) we deduce maxval(s, h
c
, l) + \(\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 4. Hence we have the identities bmc(q, m, A
1, (s, h, l)) = tt and bmc(q, m, A
2, (s, h, l)) = tt by induction hypothesis. Moreover, we have subheap(h
1, h) = tt and \(\text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) holds. As h
2 = h − h
1, by definition of bmc, we get bmc(q, m, A
1 ∗ A
2, (s, h, l
0)) = tt;
and (s, h
2) ⊧
l
A
2. For each c ∈ {1, 2}, from \(h_{c}\sqsubseteq h\) we deduce maxval(s, h
c
, l) + \(\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 4. Hence we have the identities bmc(q, m, A
1, (s, h, l)) = tt and bmc(q, m, A
2, (s, h, l)) = tt by induction hypothesis. Moreover, we have subheap(h
1, h) = tt and \(\text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) holds. As h
2 = h − h
1, by definition of bmc, we get bmc(q, m, A
1 ∗ A
2, (s, h, l
0)) = tt; - if A is A 1 −∗ A 2,:
-
let us assume bmc(q, m, A 1 −∗ A 2, (s, h, l)) = tt and prove (s, h) ⊧ l A 1 −∗ A 2. For this, we use Corollary 4.6. Let us consider h 1 ⊥ h such that \(\text {maxval}(h_{1})\leqslant \text {maxval}(s,h,l)+15|A_{1}-\!\!\!* A_{2}|q^{2}\) and (s, h 1) ⊧ l A 1 and prove
 . We have
$$\begin{array}{cl} & \text{maxval}(h_{1}) +\max(\varphi_q(A_{1}),\varphi_q(A_{2}))\\ \leqslant & \text{maxval}(s,h,l) +15|A_{1}-\!\!\!* A_{2}|q^{2} +\max(\varphi_q(A_{1}),\varphi_q(A_{2}))\\ \leqslant & \text{maxval}(s,h,l)+\varphi_q(A_{1}-\!\!\!* A_{2}) \leqslant m \end{array} $$
. We have
$$\begin{array}{cl} & \text{maxval}(h_{1}) +\max(\varphi_q(A_{1}),\varphi_q(A_{2}))\\ \leqslant & \text{maxval}(s,h,l) +15|A_{1}-\!\!\!* A_{2}|q^{2} +\max(\varphi_q(A_{1}),\varphi_q(A_{2}))\\ \leqslant & \text{maxval}(s,h,l)+\varphi_q(A_{1}-\!\!\!* A_{2}) \leqslant m \end{array} $$by Proposition 4.13 item 5. Let us prove bmc(q, m, A 1, (s, h, l)) = tt. We have \(\text {maxval}(s,h,l)+\varphi _q(A_{1})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 5. We also have \(\text {maxval}(h_{1})+\varphi _q(A_{1})\leqslant \text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\). Hence we get \(\text {maxval}(s,h_{1},l)+\varphi _q(A_{1})\leqslant m\) and by induction hypothesis, from (s, h 1) ⊧ l A 1, we get bmc(q, m, A 1, (s, h, l)) = tt. Since \(\text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) holds, by definition of we have h 1 ⊥ h and bmc(q, m, A 1, (s, h, l)) = tt. Hence, to satisfy bmc(q, m, A 1 −∗ A 2, (s, h, l)) = tt, we must have
 . The relations \(\text {maxval}(h_{1})+\varphi _q(A_{2})\leqslant \text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) hold and the relations \(\text {maxval}(s,h,l)+\varphi _q(A_{2})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) hold by Proposition 4.13 item 5. We deduce
. The relations \(\text {maxval}(h_{1})+\varphi _q(A_{2})\leqslant \text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2}))\leqslant m\) hold and the relations \(\text {maxval}(s,h,l)+\varphi _q(A_{2})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) hold by Proposition 4.13 item 5. We deduce 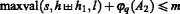 maxval and thus we have
maxval and thus we have 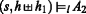 by induction hypothesis.
by induction hypothesis.Now let us assume (s, h) ⊧ l A 1 −∗ A 2 and prove bmc(q, m, A 1 −∗ A 2, (s, h, l)) = tt. By definition of bmc, we pick \(h_{1}:[0,m]\rightharpoondown [0,m]\) and we verify that either \(\text {maxval}(h_{1})+\max (\varphi _q(A_{1}),\varphi _q(A_{2})) > m\) or h 1 ⊥ h does not hold or bmc(q, m, A 1, (s, h, l)) = tt or
 . So we assume h
1 ⊥ h and
$$\text{maxval}(h_{1})+\max(\varphi_q(A_{1}),\varphi_q(A_{2})) \leqslant m $$
. So we assume h
1 ⊥ h and
$$\text{maxval}(h_{1})+\max(\varphi_q(A_{1}),\varphi_q(A_{2})) \leqslant m $$and bmc(q, m, A 1, (s, h, l)) = tt and we prove the identity
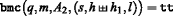 . We have \(\text {maxval}(h_{1})+\varphi _q(A_{1})\leqslant m\) and
$$\text{maxval}(s,h,l)+\varphi_q(A_{1})\leqslant \text{maxval}(s,h,l)+\varphi_q(A)\leqslant m$$
. We have \(\text {maxval}(h_{1})+\varphi _q(A_{1})\leqslant m\) and
$$\text{maxval}(s,h,l)+\varphi_q(A_{1})\leqslant \text{maxval}(s,h,l)+\varphi_q(A)\leqslant m$$by Proposition 4.13 item 5. Hence we derive \(\text {maxval}(s,h_{1},l)+\varphi _q(A_{1})\leqslant m\) thus by induction hypothesis we get (s, h 1) ⊧ l A 1. As h 1 ⊥ h we deduce
 . We have \(\text {maxval}(h_{1})+\varphi _q(A_{2})\leqslant m\) and \(\text {maxval}(s,h,l)+\varphi _q(A_{2})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 5. Hence we derive
. We have \(\text {maxval}(h_{1})+\varphi _q(A_{2})\leqslant m\) and \(\text {maxval}(s,h,l)+\varphi _q(A_{2})\leqslant \text {maxval}(s,h,l)+\varphi _q(A)\leqslant m\) by Proposition 4.13 item 5. Hence we derive 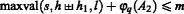 maxval and thus we get
maxval and thus we get  from the induction hypothesis.
from the induction hypothesis.
□
Appendix D: Proofs of Section 5
Proposition 5.3
(Completeness of the saturation rules) If the (finite) subset \( \text {\textsf {P}}\subseteq {\text {\textsf {Basic}}^{\mathtt {u}}}\) is closed under the rules of Fig. 4 and (s, H, L) is the canonical pre-model of P then:
-
s is a total function \( s :\mathcal {V}\rightarrow [1,q]\), hence s is a store;
-
H is a finite and functional graph, hence H is the graph of some heap h;
-
L is a singleton subset of \(\mathbb {N}\), i.e. L = {l} for some location l ;
-
the inclusion \(\text {dom}(h) \subseteq \heartsuit (s , h )\cup \{ l \}\) holds;
-
for any formula B ∈ Basic we have (s, h) ⊧ l B iff B ∈ P.
Proof
Since P is closed under the three rules
the relation {(x, y)∣ = y ∈ P} is an equivalence relation.Hence the function s is total: indeed x i = x i ∈ P and theset {j∣x i = x j ∈ P} contains at least i. Hence s(x i )is always defined and we have \({\mathtt {x}_{i}}={\mathtt {x}_{s(\mathtt {x}_{i})}}\in \text {\textsf {P}}\). Moreover we have
Since P is closed under the two rules
the relation {(i, j)∣ conv(x i , x j ) ∈ P} is a partial equivalence relation and we have
It is obvious that H is a finite graph. An important remark for the rest of the proof is the following: by construction we have
i.e. these sets are mutually disjoint. Let \(u,w\in \mathbb {N}\) be such that (u, w) ∈ H and let us check the following characteristic properties of the graph H:
- P1:
-
one of the three following properties holds:
-
either u = s(x i ) for some i ∈ [1, q];
-
or \(u=\mathfrak {h}_{i}\) for some i such that conv(x i , x i ) ∈ P;
-
or u = 0;
-
- P2:
-
if u = s( i ) then
-
either w = s(x j ) and x i ↪ x j ∈ P for some j ∈ [1, q];
-
or \(w=\mathfrak {h}_{i}\), conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_q}\}\cap \text {\textsf {P}}=\varnothing \);
-
- P3:
-
if \(\mathfrak {h}_{i}\) is defined and \(u=\mathfrak {h}_{i}\) then conv(x i , x i ) ∈ P, \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_q}\}\cap \text {\textsf {P}}=\varnothing \) and:
-
either w = s(x j ) and btwn(x i , x j ) ∈ P for some j ∈ [1, q];
-
or \(w=\mathfrak {h}_{i}\) and toloop(x i ) ∈ P;
-
or w = 0, toalloc(x i ) ∈ P and {btwn(x i , x 1),…, btwn(x i , x q ), \( \mathtt {toloop}(\mathtt {x}_{i})\}\cap \text {\textsf {P}}=\varnothing \);
-
- P4:
-
if u = 0 then \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) and:
-
either w = s(x i ) and ↪ x i ∈ P for some i ∈ [1, q];
-
or w = 0, u ↪ u ∈ P and \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \);
-
or w = 2q + 1, alloc(u) ∈ P and \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {u}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \).
-
We prove Properties P1 to P4 in that order:
-
Property P1 holds by definition of H. We just have to check that when \(u=\mathfrak {h}_{i}\) then conv(x i , x i ) ∈ P but this is a consequence of Equivalence (D.2);
-
let us check Property P2. By definition of H and Property (D.3), thereare two possibilities for (s(x i ), w) ∈ H:
-
either (s(x i ), w) = (s(x k ), s(x j )) with x k ↪ x j ∈ P. But from s(x k ) = s(x i ) we deduce x k = x i ∈ P by Equivalence (D.1). As P is closed under the rule
$$\frac{\mathtt{x}_{k}=\mathtt{x}_{i}\quad \mathtt{x}_{k}\hookrightarrow\mathtt{x}_{j}}{\mathtt{x}_{i} \hookrightarrow \mathtt{x}_{j}} $$we deduce x i ↪ x j ∈ P and v = s(x j );
-
or \((s(\mathtt {x}_{i}),w)=(s(\mathtt {x}_{k}),\mathfrak {h}_{j})\) with conv(x k , x j ) ∈ P and \(\{{\mathtt {x}_{k}}\hookrightarrow {\mathtt {x}_{1}},\ldots ,{\mathtt {x}_{k}}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). From s(x i ) = s(x k ) we deduce \(\{{\mathtt {x}_{k}}={\mathtt {x}_{i}},{\mathtt {x}_{i}}={\mathtt {x}_{k}}\}\subseteq \text {\textsf {P}}\) by Equivalence (D.1). But P is closed under the rule
$$\frac{\mathtt{x}_{k}=\mathtt{x}_{i}\quad\mathtt{conv}(\mathtt{x}_{k},\mathtt{x}_{j})}{\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{j})}~\;\frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{j})}{\mathtt{conv}(\mathtt{x}_{j}, \mathtt{x}_{i})}~\; \frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{j})\quad\mathtt{conv}(\mathtt{x}_{j}, \mathtt{x}_{i})}{\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{i})}~\; \frac{\mathtt{x}_{i}=\mathtt{x}_{k} \quad\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{p}}{\mathtt{x}_{k} \hookrightarrow \mathtt{x}_{p}} $$hence we deduce {conv(x i , x j ), conv(x i , x i )} ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). We conclude \(w=\mathfrak {h}_{j}=\mathfrak {h}_{i}\) using Equivalence (D.2);
-
-
let us check Property P3. By definition of H and Property (D.3), there are three possibilities for \((\mathfrak {h}_{i},w)\in H\):
-
either \((\mathfrak {h}_{i},w)=(\mathfrak {h}_{k},s(\mathtt {x}_{j}))\) with btwn(x k , x j ) ∈ P and \(\{{\mathtt {x}_{k}}\hookrightarrow {\mathtt {x}_{1}},\ldots ,{\mathtt {x}_{k}} \hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). We deduce \(\mathfrak {h}_{i}=\mathfrak {h}_{k}\) and w = s(x j ). Thus \(\{\mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{k}), \mathtt {conv}(\mathtt {x}_{k},\mathtt {x}_{i}), \mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{i})\}\subseteq \text {\textsf {P}}\) by Equivalence (D.2). Since P is closed under the rules
$$\frac{\mathtt{conv}(\mathtt{x}_{k},\mathtt{x}_{i})\quad\mathtt{btwn}(\mathtt{x}_{k},\mathtt{x}_{j})}{\mathtt{btwn} (\mathtt{x}_{i},\mathtt{x}_{j})}\qquad\frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{k})\quad\mathtt{x}_{i} \hookrightarrow\mathtt{x}_{p}}{\mathtt{x}_{k}\hookrightarrow\mathtt{x}_{p}} $$we deduce btwn(x i , x j ) ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x }_{1}}, \ldots , \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \);
-
\((\mathfrak {h}_{i},w)=({\mathfrak {h}_{k}},{\mathfrak {h}_{j}})\) with \(\{\mathtt {conv}(\mathtt {x}_{k}, \mathtt {x}_{j}), \mathtt {toloop}(\mathtt {x}_{k})\}\subseteq \text {\textsf {P}}\) and \(\{{\mathtt {x}_{k}} \hookrightarrow {\mathtt {x}_{1}},\ldots ,{\mathtt {x}_{k}}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). We deduce \(\mathfrak {h}_{i} = \mathfrak {h}_{k}\) and \(w = \mathfrak {h}_{j}\). We get \(\{\mathtt {conv}(\mathtt {x}_{i}, \mathtt {x}_{k}), \mathtt {conv}(\mathtt {x}_{k},\mathtt {x}_{i}),\mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{i})\}\subseteq \text {\textsf {P}}\) using Equivalence (D.2). Since P is closed under the rules
$$\frac{\mathtt{conv}(\mathtt{x}_{k},\mathtt{x}_{i})\quad\mathtt{toloop}(\mathtt{x}_{k})}{\mathtt{toloop}(\mathtt{x}_{i})} \qquad \frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{k})\quad\mathtt{x}_{i}\hookrightarrow \mathtt{x}_{p}}{\mathtt{x}_{k}\hookrightarrow \mathtt{x}_{p}} $$we deduce toloop(x i ) ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}}, \ldots , \mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \);
-
(\(\mathfrak {h}_{i},w\)) = (\(\mathfrak {h}_{k},0\)) with toalloc(x k ) ∈ P and {x k ↪ x 1, …, x k ↪ x q , btwn(x k , x 1), …, btwn(x k , x q ), toloop(x k )} \(\cap \) \(\text {\textsf {P}}=\varnothing \). We deduce \(\mathfrak {h}_{i}\) = \(\mathfrak {h}_{k}\) and w = 0. We get {conv(x i , x k ), conv(x k , x i ), conv(x i , x i )} \(\subseteq \text {\textsf {P}}\) using Equivalence (D.2). Since P is closed under the rules
$$\begin{array}{cc} \frac{\mathtt{conv}(\mathtt{x}_{k},\mathtt{x}_{i})\quad\mathtt{toalloc}(\mathtt{x}_{k})}{\mathtt{toalloc} (\mathtt{x}_{i})} &{\qquad} \frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{k})\quad\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{p}}{\mathtt{x}_{k} \hookrightarrow\mathtt{x}_{p}}\\[3ex] \frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{k})\quad\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{p})}{\mathtt{btwn} (\mathtt{x}_{k},\mathtt{x}_{p})} &{\qquad} \frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{k})\quad\mathtt{toloop}(\mathtt{x}_{i})}{\mathtt{toloop}(\mathtt{x}_{k})} \end{array} $$we deduce toalloc(x i ) ∈ P and {x i ↪ x 1,…, x i ↪ x q , \( \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{1}),\ldots , \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{q}), \mathtt {toloop}(\mathtt {x}_{i})\}\cap \text {\textsf {P}}=\varnothing \);
-
-
let us finally check Property P4. By definition of H and Property (D.3), there are three possibilities for (0, w) ∈ H:
-
(0,w) = (0, s(x i )) with u ↪ x i ∈ P and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u}, \ldots , {\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \); Hence w = s(x i ) and all the other properties hold;
-
(0, w) = (0, 0) with u ↪ u ∈ P and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}, \mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). Hence w = 0 and all the other properties hold;
-
(0, w) = (0, 2q + 1) with alloc(u) ∈ P and \(\{{\mathtt {x}_{1}}={\mathtt {u}}, \ldots , {\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}} \hookrightarrow \mathtt {u}, \mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {u}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \). Hence w = 2q + 1 and all the other properties hold.
-
We can now check that H is a functional graph. Assume that \(\{(u,v),(u,w)\}\subseteq H\). Let us show v = w. We have three cases:
-
either u = s(x i )
-
v = s(x j ) and w = s(x k ) with \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{j}},\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{k}}\} \subseteq \text {\textsf {P}}\). But P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{j}\quad\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{k}}{\mathtt{x}_{j}= \mathtt{x}_{k}} $$hence x j = x k ∈ P and thus v = s(x j ) = s(x k ) = w by Equivalence (D.1);
-
v = s(x j ) and \(w=\mathfrak {h}_{i}\) is impossible because \(\{\mathtt {x}_{i} \hookrightarrow {\mathtt {x}_{1}}, \ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \) contradicts x i ↪ x j ∈ P;
-
\(v=\mathfrak {h}_{i}\) and \(w=\mathfrak {h}_{i}\) imply v = w;
-
-
or \(u=\mathfrak {h}_{i}\) with conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i} \hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \)
-
v = s(x j ) and w = s(x k ) with \(\{\mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j}), \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{k})\}\subseteq \text {\textsf {P}}\). But P is closed under the rule
$$\frac{\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{j})\quad \mathtt{btwn}(\mathtt{x}_{i}, \mathtt{x}_{k})}{\mathtt{x}_{j}= \mathtt{x}_{k}} $$hence x j = x k ∈ P and thus v = s(x j ) = s(x k ) = w by Equivalence (D.1);
-
v = s(x j ) and \(w=\mathfrak {h}_{i}\) with \(\{\mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{j}), \mathtt {toloop}(\mathtt {x}_{i})\}\subseteq \text {\textsf {P}}\). But P is closed under the rule
$$\frac{\mathtt{toloop}(\mathtt{x}_{i})\quad\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{j})}{\mathtt{x}_{i}\hookrightarrow \mathtt{x}_{j}} $$hence we deduce x i ↪ x j which contradicts \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}}, \ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \);
-
v = s(x j ) and w = 0 is impossible because btwn(x i , x j ) ∈ P contradicts
$$\{\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{1}),\ldots,\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{q}), \mathtt{toloop}(\mathtt{x}_{i})\}\cap\text{\textsf{P}}=\varnothing; $$ -
\(v=\mathfrak {h}_{i}\) and \(w=\mathfrak {h}_{i}\) implies v = w;
-
\(v=\mathfrak {h}_{i}\) and w = 0 is impossible because toloop(x i ) ∈ P contradicts
$$\{\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{1}),\ldots,\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{q}), \mathtt{toloop}(\mathtt{x}_{i})\}\cap\text{\textsf{P}}=\varnothing; $$ -
v = 0 and w = 0 implies v = w;
-
-
or u = 0 with \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}} \hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \)
-
v = s( i ) and w = s(x j ) with \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{i}},\mathtt {u} \hookrightarrow {\mathtt {x}_{j}}\}\subseteq \text {\textsf {P}}\). But P is closed under the rule
$$\frac{\mathtt{u}\hookrightarrow\mathtt{x}_{i}\quad\mathtt{u}\hookrightarrow\mathtt{x}_{j}}{\mathtt{x}_{i}= \mathtt{x}_{j}} $$hence x i = x j ∈ P and thus v = s(x i ) = s(x j ) = w by Equivalence (D.1);
-
v = s(x i ) and w = 0 is impossible because u ↪ x i ∈ P contradicts \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \);
-
v = s(x i ) and w = 2q + 1 is impossible because u ↪ x i ∈ P contradicts \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {u}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \);
-
v = 0 and w = 0 implies v = w;
-
v = 0 and w = 2q + 1 is impossible because u ↪ u ∈ P contradicts \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {u}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \);
-
v = 2q + 1 and w = 2q + 1 implies v = w.
-
Let us now show that L is a singleton set. For that, we first show that L contains no more than one location:
-
if s(x i ) ∈ L and s(x j ) ∈ L then \(\{{\mathtt {x}_{i}}=\mathtt {u},{\mathtt {x}_{j}}=\mathtt {u}\}\subseteq \text {\textsf {P}}\). But P is closed under the rules
$$\frac{\mathtt{x}_{j}=\mathtt{u}}{\mathtt{u}=\mathtt{x}_{j}}\qquad\frac{\mathtt{x}_{i}=\mathtt{u}\quad\mathtt{u}= \mathtt{x}_{j}}{\mathtt{x}_{i}=\mathtt{x}_{j}} $$thus x i = x j ∈ P and s(x i ) = s(x j );
-
s(x i ) ∈ L and \(\mathfrak {h}_{j}\in L\) is impossible because x i = u ∈ P contradicts \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}\}\cap \text {\textsf {P}}= \varnothing \);
-
the case when s(x i ) ∈ L and 0 ∈ L is impossible because x i = u ∈ P contradicts \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}},\ldots \}\cap \text {\textsf {P}}=\varnothing \);
-
if \(\mathfrak {h}_{i}\in L\) and \(\mathfrak {h}_{j}\in L\) then we have {x i ↪ u, x j ↪ u} ∈ P. But P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{u}\quad\mathtt{x}_{j}\hookrightarrow\mathtt{u}}{\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{j})} $$hence conv(x i , x j ) ∈P and thus \(\mathfrak {h}_{i}=\mathfrak {h}_{j}\);
-
\(\mathfrak {h}_{i}\in L\) and 0 ∈ L is impossible because x i ↪ u ∈ P contradicts \(\{\ldots , {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \).
Then we show that L is not empty. If there exists i such that x i = u ∈ P then s(x i ) ∈ L. Otherwise we have \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}\}\cap \text {\textsf {P}}=\varnothing \). If there exists j such that x j ↪ u ∈ P then, because P is closed under the rule
we have conv(x j , x j ) ∈ P and thus \(\mathfrak {h}_{j}\) is defined (see Equivalence (D.2)) and we deduce \(\mathfrak {h}_{j}\in L\). Otherwise \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) and in that case 0 ∈ L.
We consider the memory state (s, h) and the location l such that H is the graph of the heap h and L = {l}. Let us show that the inclusion \(\text {dom}(h)\subseteq \heartsuit (s,h)\cup \{ l\}\) holds. For this we show that the three following properties hold:
-
\(\text {dom}(h)\subseteq \{ s(\mathtt {x}_{i})\mid i\in [1,q]\} \cup \{\mathfrak {h}_{i}\mid i\in [1,q]\text { and }\mathfrak {h}_{i}\text { is defined}\}\cup \{0\}\);
-
\(\{ s(\mathtt {x}_{i})\mid i\in [1,q]\} \cup \{\mathfrak {h}_{i}\mid i\in [1,q]\text { and }\mathfrak {h}_{i}\text { is defined}\}\subseteq \mathfrak {p}\heartsuit (s,h)\);
-
if 0 ∈ dom(h) then l = 0.
The first property is trivial by definition of H. Forthe second property, we first notice that \(\{ s(\mathtt {x}_{i})\mid i\in [1,q]\}\subseteq \mathfrak {p}\heartsuit (s,h)\). Then if \(\mathfrak {h}_{i}\) is defined then conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}= \varnothing \) by characteristic Property P3 of H. Hence we have \((s(\mathtt {x}_{i}),\mathfrak {h}_{i})\in H\) and we deduce \(\mathfrak {h}_{i}\in h(s(\{\mathtt {x}_{1},\ldots , \mathtt {x}_{q}\}))\). Finally, if 0 ∈ dom(h) then by characteristic Property P4 of H we have {x 1 = u,…, x q = u, x 1 ↪ u, \(\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) and as a consequence we get 0 ∈ L by definition of L. Hence l = 0.
From the three previous properties we deduce \(\text {dom}(h)\subseteq \mathfrak {p}\heartsuit (s,h)\cup \{ l\}\) and hence the inclusion \(\text {dom}(h)\subseteq \heartsuit (s,h)\cup \{ l\}\) holds.
Let us finally show that for any basic formula B ∈ Basic we have (s, h) ⊧ l B iff B ∈ P. We proceed by case analysis on B:
- if B is x i = x j .:
-
Then (s, h) ⊧ l x i = x j iff s(x i ) = s(x j ) iff x i = x j ∈ P by Equivalence (D.1);
- if B is x i ↪ x j .:
-
Let us first assume (s, h) ⊧ l x i ↪ x j and show x i ↪ x j ∈ P. We have h(s(x i )) = s(x j ) hence (s(x i ), s(x j )) ∈ H. By the characteristic Property P2 of H and Property (D.3), the only possibility is that there exists k such that s(x j ) = s(x k ) and x i ↪ x k ∈ P. Hence by Equivalence (D.1), we have x k = x j ∈ P. But P is closed under the rule
$$\frac{\mathtt{x}_{k}=\mathtt{x}_{j}\quad\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{k}}{\mathtt{x}_{i}\hookrightarrow \mathtt{x}_{j}} $$hence we derive x i ↪ x j ∈ P.
Let us now assume x i ↪ x j ∈ P. Then (s(x i ), s(x j )) ∈ H by definition of H and thus (s, h) ⊧ l x i ↪ x j ;
- if B is x( i , x j ).:
-
Let us first assume (s, h) ⊧ l conv(x i , x j ) and show conv(x i , x j ) ∈ P. We have the equations h(s(x i )) = h(s(x j )) = v. Hence \(\{(s(\mathtt {x}_{i}),v),(s(\mathtt {x}_{j}),v)\}\subseteq H\). By the characteristic Property P2 of H and Property (D.3), we have two cases:
-
v = s(x k ) and v = s(x r ) with \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{k}},\mathtt {x}_{j}\hookrightarrow {\mathtt {x}_{r}}\}\subseteq \text {\textsf {P}}\). We deduce s(x k ) = s(x r ) and thus x k = x r ∈ P by Equivalence (D.1). But P is closed under the rules
$$\frac{\mathtt{x}_{k}=\mathtt{x}_{r}\quad\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{k}}{\mathtt{x}_{i}\hookrightarrow \mathtt{x}_{r}} \qquad\frac{\mathtt{x}_{i}\hookrightarrow \mathtt{x}_{r}\quad\mathtt{x}_{j}\hookrightarrow \mathtt{x}_{r}}{\mathtt{conv}({\mathtt{x}_{i}},{\mathtt{x}_{j}})} $$hence we get conv(x i , x j ) ∈ P;
-
\(v=\mathfrak {h}_{i}\) and \(v=\mathfrak {h}_{j}\) with \(\{\mathtt {conv}(\mathtt {x}_{i},\mathtt {x}_{i}),\mathtt {conv}(\mathtt {x}_{j}, \mathtt {x}_{j})\}\subseteq \text {\textsf {P}}\). From \(\mathfrak {h}_{i}=\mathfrak {h}_{j}\), we get conv(x i , x j ) ∈ P by Equivalence (D.2);
Now let us assume conv(x i , x j ) ∈ P and let us show (s, h) ⊧ l conv(x i , x j ). We have two cases:
-
if x i ↪ x k ∈ P holds for some k ∈ [1, q] then as P is closed under the rule
$$\frac{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{j})\quad\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{k}}}{\mathtt{x}_{j} \hookrightarrow{\mathtt{x}_{k}}} $$then x j ↪ x k ∈ P and \(\{(s(\mathtt {x}_{i}),s(\mathtt {x}_{k})),(s(\mathtt {x}_{j}),s(\mathtt {x}_{k}))\}\subseteq H\) by definition of H. Hence (s, h) ⊧ l conv(x i , x j );
-
otherwise \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\} \cap \text {\textsf {P}}= \varnothing \). From conv(x i , x j ) ∈ P we deduce \(\mathfrak {h}_{i}=\mathfrak {h}_{j}\) and conv(x j , x j ) ∈ P by Equivalence (D.2). By definition of H we get \(\{(s(\mathtt {x}_{i}),\mathfrak {h}_{j}),(s(\mathtt {x}_{j}),\mathfrak {h}_{j})\}\subseteq H\) and we conclude (s, h) ⊧ l conv(x i , x j );
-
- if B is btwn(x i , x j ).:
-
Let us first assume (s, h) ⊧ l btwn(x i , x j ) and show btwn(x i , x j ) ∈ P. We have the inclusion \(\{(s(\mathtt {x}_{i}),v),(v, s(\mathtt {x}_{j}))\}\subseteq H\) for some v. By characteristic Property P2 of H, we have two cases:
-
v = s(x k ) with x i ↪ x k ∈ P. From (s(x k ), s(x j )) ∈ H we deduce (s, h) ⊧ l x k ↪ x j and thus x k ↪ x j ∈ P (from the earlier case B = x k ↪ x j ). Since P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{k}}\quad{\mathtt{x}_{k}}\hookrightarrow{\mathtt{x}_{j}}}{\mathtt{btwn} (\mathtt{x}_{i},\mathtt{x}_{j})} $$we deduce btwn(x i , x j ) ∈ P;
-
\(v=\mathfrak {h}_{i}\) with conv(x i , x i ) and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}}, \ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). By characteristic Property P3 of H and Property (D.3), there is only one possible case for \((\mathfrak {h}_{i}, s(\mathtt {x}_{j}))\in H\): there must exist k such that s(x j ) = s(x k ) and btwn(x i , x k ) ∈ P. By Equivalence (D.1), we deduce x k = x j ∈ P. Since P is closed under the rule
$$\frac{\mathtt{x}_{k}=\mathtt{x}_{j}\quad\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{k})}{\mathtt{btwn}(\mathtt{x}_{i}, \mathtt{x}_{j})} $$wededuce ( i , j ) ∈P;
Now let us assume x(x i , x j ) ∈ P and let us show (s, h) ⊧ l btwn(x i , x j ). We have two cases:
-
either x i ↪ x k ∈ P holds for some k ∈ [1, q]. As P is closed under therule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{k}}\quad\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{j})}{\mathtt{x}_{k} \hookrightarrow\mathtt{x}_{j}} $$we deduce x k ↪ x j ∈ P and thus we have \(\{(s(\mathtt {x}_{i}),s(\mathtt {x}_{k})),(s(\mathtt {x}_{k}), s(\mathtt {x}_{j}))\}\subseteq H\) by definition of H. As a consequence, we get (s, h) ⊧ l btwn(x i , x j );
-
or \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\} \cap \text {\textsf {P}}=\varnothing \). Since P is closed under the rule
$$\frac{\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{j})}{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{i})} $$we deduce conv(x i , x i ) ∈ P and thus \(\{(s(\mathtt {x}_{i}),\mathfrak {h}_{i}),(\mathfrak {h}_{i}, s(\mathtt {x}_{j}))\}\subseteq H\) by definition of H. As a consequence we derive (s, h) ⊧ l btwn(x i , x j );
-
- if B is toloop(x i ).:
-
Let us first assume (s, h) ⊧ l toloop(x i ) and show toloop(x i ) ∈ P. We thus have the inclusion \(\{(s(\mathtt {x}_{i}),v),(v,v)\}\subseteq H\) for some \(v\in \mathbb {N}\). By characteristic Property P2 of H, we have two cases for (s(x i ), v) ∈ H:
-
v = s(x j ) with x i ↪ x j ∈ P. From (s(x j ), s(x j )) ∈ H we deduce (s, h) ⊧ l x j ↪ x j and thus x j ↪ x j ∈ P (from the earlier case B = x j ↪ x j ). Since P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}\quad\mathtt{x}_{j}\hookrightarrow{\mathtt{x}_{j}}}{\mathtt{toloop} (\mathtt{x}_{i})} $$we deduce ( i ) ∈ P;
-
\(v=\mathfrak {h}_{i}\) with conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i} \hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). By characteristic Property P3 of H and Property (D.3), from \((\mathfrak {h}_{i},\mathfrak {h}_{i})\in H\) we deduce toloop(x i ) ∈ P;
Now let us assume toloop(x i ) ∈ P and let us show (s, h) ⊧ l toloop(x i ). We have two cases:
-
either x i ↪ x j ∈ P holds for some j ∈ [1, q]. As P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}\quad\mathtt{toloop}(\mathtt{x}_{i})}{\mathtt{x}_{j}\hookrightarrow {\mathtt{x}_{j}}} $$we deduce x j ↪ x j ∈ P and thus we have both (s, h) ⊧ l x i ↪ x j and (s, h) ⊧ l x j ↪ x j (from theearlier cases B = x i ↪ x j and B = x j ↪ x j ). Hence we derive (s, h) ⊧ l toloop(x i );
-
or \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}} \}\cap \text {\textsf {P}}= \varnothing \). As P is closed under the rules
$$\frac{\mathtt{toloop}(\mathtt{x}_{i})}{\mathtt{toalloc}(\mathtt{x}_{i})} \qquad \frac{\mathtt{toalloc}(\mathtt{x}_{i})}{\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{i})} $$we get conv(x i , x i ) ∈ P and thus \(\{(s(\mathtt {x}_{i}),\mathfrak {h}_{i}),(\mathfrak {h}_{i},\mathfrak {h}_{i})\}\subseteq H\) by definition of H. Hence (s, h) ⊧ l toloop(x i );
-
- if B is toalloc(x i ).:
-
Let us first assume (s, h) ⊧ l toalloc(x i ) and show toalloc(x i ) ∈ P. We have \(\{(s(\mathtt {x}_{i}),v),(v,w)\}\subseteq H\) for some \(v,w\in \mathbb {N}\). By characteristic Property P2 of H, we have two cases for (s(x i ), v) ∈ H:
-
v = s(x j ) with x i ↪ x j ∈ P. From (s(x j ), w) ∈ H we deduce (s, h) ⊧ l conv(x j , x j ) and thus conv(x j , x j ) ∈ P(from the earliercase B = ( j , j )). Since P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}\quad\mathtt{conv}(\mathtt{x}_{j}, \mathtt{x}_{j})}{\mathtt{toalloc}(\mathtt{x}_{i})} $$we deduce toalloc(x i ) ∈ P;
-
\(v=\mathfrak {h}_{i}\) with conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i} \hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). By characteristic Property P3 of H, we have three cases for \((\mathfrak {h}_{i},w)\in H\).
-
w = s(x j ) with btwn(x i , x j ) ∈ P. But P is closed under the rule
$$\frac{\mathtt{btwn}(\mathtt{x}_{i},\mathtt{x}_{j})}{\mathtt{toalloc}(\mathtt{x}_{i})} $$hence toloop(x i ) ∈ P;
-
\(w=\mathfrak {h}_{i}\) with toloop(x i ) ∈ P. But P is closed under the rule
$$\frac{\mathtt{toloop}(\mathtt{x}_{i})}{\mathtt{toalloc}(\mathtt{x}_{i})} $$hence toloop(x i ) ∈ P;
-
w = 0 and inthis case toloop(x i ) ∈ P;
-
Now let us assume toalloc(x i ) ∈ P and let us show (s, h) ⊧ l toalloc(x i ). We have four cases:
-
either x i ↪ x j ∈ P holds for some j ∈ [1, q]. As P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}\quad\mathtt{toalloc}(\mathtt{x}_{i})}{\mathtt{conv}(\mathtt{x}_{j}, \mathtt{x}_{j})} $$we deduce (x j , x j ) ∈P and thus we have both (s, h) ⊧ l x i ↪ x j and (s, h) ⊧ l conv(x j , x j ) (from theearlier cases B = x i ↪ x j and B = conv(x j , x j )). Hence we get (s, h) ⊧ l toalloc(x i );
-
or \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \) and btwn(x i , x j ) ∈ P for some j ∈ [1, q]. Then we have (s, h) ⊧ l btwn(x i , x j ) (from the earlier case B = btwn(x i , x j )). We get (s, h) ⊧ l toalloc(x i );
-
or \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{1}),\ldots ,\mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{q})\}\cap \text {\textsf {P}}=\varnothing \) and toloop(x i ) ∈ P. Then we have (s, h) ⊧ l toloop(x i ) (from the earlier case B = toloop(x i )). We deduce (s, h) ⊧ l toalloc(x i );
-
or \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{1}),\ldots ,\mathtt {btwn}(\mathtt {x}_{i},\mathtt {x}_{q}), \mathtt {toloop}(\mathtt {x}_{i})\}\cap \text {\textsf {P}}=\varnothing \). But since P is closed under the rule
$$\frac{\mathtt{toalloc}(\mathtt{x}_{i})}{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{i})} $$we deduce conv(x i , x i ) ∈ P and thus \(\{(s(\mathtt {x}_{i}),\mathfrak {h}_{i}),(\mathfrak {h}_{i},0)\}\subseteq H\) hence we conclude (s, h) ⊧ l toalloc(x i );
-
- if B is x i = u.:
-
Let us first assume (s, h) ⊧ l x i = u and show x i = u ∈ P. We have l = s(x i ). According to the definitionof L and Property (D.3), we must have l = s(x j ) with x j = u ∈ P. But then we have s(x i ) = s(x j ) hence x i = x j ∈ P by Equivalence (D.1). As P is closed under the rule
$$\frac{{\mathtt{x}_{i}}={\mathtt{x}_{j}}\quad{\mathtt{x}_{j}}=\mathtt{u}}{{\mathtt{x}_{i}}=\mathtt{u}} $$we get x i = u ∈ P.
Conversely, if we assume x i = u ∈ P then by definition of L we have s(x i ) ∈ L and thus l = s(x i ). As a consequence,we have (s, h) ⊧ l x i = u;
- if B is x i ↪ u.:
-
Let us first assume (s, h) ⊧ l x i ↪ u and show x i ↪ u ∈ P. We have (s(x i ), l) ∈ H. By the characteristic Property P2 of H, we have two cases:
-
either l = s(x j ) with x i ↪ x j ∈ P for some j ∈ [1, q]. We derive (s, h) ⊧ l x i ↪ x j from the earliercase B = x i ↪ x j and thus weget (s, h) ⊧ l x j = u. Hence we have x j = u ∈ P (from theearlier case B = x j = u). As P is closed under the rule
$$\frac{{\mathtt{x}_{j}}=\mathtt{u}\quad\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}}{\mathtt{x}_{i}\hookrightarrow \mathtt{u}} $$we get x i ↪ u ∈ P;
-
or \( l=\mathfrak {h}_{i}\). But in that case, according to the definition of L and Property (D.3), we must have x i ↪ u ∈ P;
Now let us assume x i ↪ u ∈ P and let us show (s, h) ⊧ l x i ↪ u. We have two cases:
-
either x j = ∈ P for some j ∈ [1, q]. As P is closed under the rules
$$\frac{{\mathtt{x}_{j}}=\mathtt{u}}{\mathtt{u}={\mathtt{x}_{j}}}\qquad \frac{\mathtt{u}={\mathtt{x}_{j}}\quad \mathtt{x}_{i}\hookrightarrow\mathtt{u}}{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{j}}} $$we get x i ↪ x j ∈ P. Then we have (s, h) ⊧ l x j = u and (s, h) ⊧ l x i ↪ x j (from the earlier cases B = x j = u and B = x i ↪ x j ). Hence we deduce (s, h) ⊧ l x i ↪ u;
-
or \(\{{\mathtt {x}_{1}}=\mathtt {u},\ldots ,{\mathtt {x}_{q}}=\mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) and in that case \( l=\mathfrak {h}_{i}\). But P is closed under the rules
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{u}\quad\mathtt{x}_{i}\hookrightarrow\mathtt{u}}{\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{i})}\qquad \frac{\mathtt{x}_{i}\hookrightarrow\mathtt{x}_{p}\quad\mathtt{x}_{i}\hookrightarrow \mathtt{u}}{\mathtt{x}_{p}= \mathtt{u}} $$hence conv(x i , x i ) ∈ P and \(\{\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{i}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). Thus \((s(\mathtt {x}_{i}),\mathfrak {h}_{i}= l)\in H\) by definition of H. We conclude (s, h) ⊧ l x i ↪ u;
-
- if B is u ↪ x i .:
-
Let us first assume (s, h) ⊧ l u ↪ x i and show u ↪ x i ∈P.
Accordingto the definition of L, for l ∈ L we have three cases:
-
either l = s(x j ) with x j = u ∈ P for some j ∈ [1, q]. From (s(x j ), s(x i )) ∈ H, using characteristic Property P2 of H and Property (D.3), we deduce x j ↪ x i ∈ P. But P is closed under the rule
$$\frac{{\mathtt{x}_{j}}=\mathtt{u}\quad\mathtt{x}_{j}\hookrightarrow{\mathtt{x}_{i}}}{\mathtt{u}\hookrightarrow {\mathtt{x}_{i}}} $$hence we get u ↪ x i ∈ P;
-
or \( l=\mathfrak {h}_{j}\) with x j ↪ u ∈ P for some j ∈ [1, q]. From \((\mathfrak {h}_{j},s(\mathtt {x}_{i}))\in H\), using characteristic Property P3 of H and Property (D.3), we deduce btwn(x j , x i ) ∈ P. Since P is closed under the rule
$$\frac{\mathtt{x}_{j}\hookrightarrow\mathtt{u}\quad\mathtt{btwn}(\mathtt{x}_{j},\mathtt{x}_{i})}{\mathtt{u} \hookrightarrow{\mathtt{x}_{i}}} $$we get u ↪ x i ∈ P;
-
or l = 0. From (0, s(x i )) ∈ H, using characteristicProperty P4 of H and Property (D.3), we deduce s(x i ) = s(x j ) and u ↪ x j ∈ P. From Equivalence (D.1) we get x j = x i ∈ P and as P is closed under the rule
$$\frac{{\mathtt{x}_{j}}={\mathtt{x}_{i}}\quad\mathtt{u}\hookrightarrow{\mathtt{x}_{j}}}{\mathtt{u}\hookrightarrow {\mathtt{x}_{i}}} $$we conclude u ↪ i ∈ P;
Now let us assume u ↪ x i ∈ P and let us show (s, h) ⊧ l ↪ x i . We have three cases for l ∈ L:
-
either l = s(x j ) with x j = ∈ P for some j ∈ [1, q]. As P is closed under the rules
$$\frac{\mathtt{x}_{j}=\mathtt{u}}{\mathtt{u}=\mathtt{x}_{j}}\qquad \frac{\mathtt{u}=\mathtt{x}_{j}\quad\mathtt{u}\hookrightarrow{\mathtt{x}_{i}}}{{\mathtt{x}_{j}}\hookrightarrow {\mathtt{x}_{i}}} $$we get x j ↪ x i ∈ P and thus (s, h) ⊧ l x j ↪ x i from the earlier case B = x j ↪ x i . We deduce (s, h) ⊧ l u ↪ x i ;
-
or \( l=\mathfrak {h}_{j}\) with x j ↪ u ∈ P and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}\}\cap \text {\textsf {P}}=\varnothing \). As P is closed under the rules
$$\frac{\mathtt{x}_{j}\hookrightarrow\mathtt{u}\quad\mathtt{u}\hookrightarrow\mathtt{x}_{i}}{\mathtt{btwn} (\mathtt{x}_{j},\mathtt{x}_{i})} \qquad \frac{\mathtt{x}_{j}\hookrightarrow\mathtt{x}_{p}\quad \mathtt{x}_{j} \hookrightarrow\mathtt{u}}{\mathtt{x}_{p}=\mathtt{u}} $$we get btwn(x j , x i ) ∈ P and \(\{\mathtt {x}_{j}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {x}_{j}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). Hence by definition of H we get \((\mathfrak {h}_{j},s(\mathtt {x}_{i}))\in H\). We deduce (s, h) ⊧ l u ↪ x i ;
-
or l = 0 and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \). Then (0, s(x i )) ∈ H by definition of H and we deduce (s, h) ⊧ l u ↪ x i ;
-
- if B is u ↪ u.:
-
Let us first assume (s, h) ⊧ l u ↪ u and show u ↪ u ∈ P. According to the definition of L, for l ∈ L we have three cases:
-
either l = s(x i ) with x i = ∈ P for some i ∈ [1, q]. From the earlier case B = x i = u we deduce (s, h) ⊧ l x i = u. Hence we get (s, h) ⊧ l x i ↪ x i and as a consequence x i ↪ x i ∈ P. But P is closed under the rules
$$\frac{{\mathtt{x}_{i}}=\mathtt{u}\quad\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{i}}}{\mathtt{u}\hookrightarrow {\mathtt{x}_{i}}} \qquad \frac{{\mathtt{x}_{i}}=\mathtt{u}\quad\mathtt{u}\hookrightarrow {\mathtt{x}_{i}}}{\mathtt{u} \hookrightarrow \mathtt{u}} $$hence u ↪ u ∈ P;
-
or \( l=\mathfrak {h}_{i}\) with x i ↪ u ∈ P and \(\{{\mathtt {x}_{1}}=\mathtt {u},\ldots {\mathtt {x}_{q}}=\mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) for some i ∈ [1, q]. We deduce (s, h) ⊧ l x i ↪ u from the earlier case B = x i ↪ u. Hence we derive (s, h) ⊧ l toloop(x i ) and thus toloop(x i ) ∈ P from the earlier case B = toloop(x i ). But P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{u}\quad\mathtt{toloop}(\mathtt{x}_{i})}{\mathtt{u}\hookrightarrow\mathtt{u}} $$hence u ↪ u ∈ P;
-
or l = 0. Then (0, 0) ∈ H and by characteristicProperty P4 of H and Property (D.3), we must have u ↪ u ∈ P;
Now let us assume u ↪ u ∈ P and let us show (s, h) ⊧ l ↪ u. We have three cases for l ∈ L we have three cases:
-
either l = s(x i ) with x i = u ∈ P for some i ∈ [1, q]. As P is closed under the rules
$$\frac{{\mathtt{x}_{i}}=\mathtt{u}}{\mathtt{u}={\mathtt{x}_{i}}} \qquad \frac{\mathtt{u}={\mathtt{x}_{i}}\quad \mathtt{u}\hookrightarrow\mathtt{u}}{\mathtt{x}_{i}\hookrightarrow\mathtt{u}} \qquad \frac{\mathtt{u}= {\mathtt{x}_{i}}\quad\mathtt{x}_{i}\hookrightarrow\mathtt{u}}{\mathtt{x}_{i}\hookrightarrow{\mathtt{x}_{i}}} $$we get x i ↪ x i ∈ P hence (s, h) ⊧ l x i ↪ x i (from theearlier case B = x i ↪ x i ). Since l = s(x i ) we deduce (s, h) ⊧ l u ↪ u;
-
or \( l=\mathfrak {h}_{i}\) with x i ↪ u ∈ P. As P is closed under the rule
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{u}\quad\mathtt{u}\hookrightarrow\mathtt{u}}{\mathtt{toloop}(\mathtt{x}_{i})} $$we get toloop(x i ) ∈ P. From the earlier cases B = x i ↪ u and B = toloop(x i ) we deduce (s, h) ⊧ l x i ↪ u and (s, h) ⊧ l toloop(x i ) hence (s, h) ⊧ l u ↪ u;
-
or l = 0 and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \). As P is closed under the rule
$$\frac{\mathtt{u}\hookrightarrow\mathtt{x}_{p}\quad\mathtt{u}\hookrightarrow\mathtt{u}}{\mathtt{x}_{p}=\mathtt{u}} $$we deduce \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\} \cap \text {\textsf {P}}=\varnothing \) and then (0, 0) ∈ H by the definition of H and we conclude (s, h) ⊧ l u ↪ u;
-
- if B is alloc(u).:
-
Let us first assume (s, h) ⊧ l alloc(u) and show alloc(u) ∈ P. According to the definition of L, for l ∈ L we have three cases:
-
either l = s(x i ) with x i = u ∈ P for some i ∈ [1, q]. We deduce s(x i ) ∈ dom(h) and thus (s, h) ⊧ l conv(x i , x i ). Using the earlier case B = conv(x i , x i ), we get conv(x i , x i ) ∈ P. But P is closed under the rule
$$\frac{{\mathtt{x}_{i}}=\mathtt{u}\quad\mathtt{conv}(\mathtt{x}_{i}, \mathtt{x}_{i})}{\mathtt{alloc}(\mathtt{u})} $$hence alloc(u) ∈ P;
-
or \( l=\mathfrak {h}_{i}\) with x i ↪ u ∈ P for some i ∈ [1, q]. Using the earlier case B = x i ↪ u, we deduce (s, h) ⊧ l x i ↪ u and then (s, h) ⊧ l toloop(x i ). Hence we get toalloc(x i ) ∈ P (from the earlier case B = toalloc(x i )). As P is closed under the rule
$$\frac{\mathtt{toalloc}(\mathtt{x}_{i})\quad\mathtt{x}_{i}\hookrightarrow\mathtt{u}}{\mathtt{alloc}(\mathtt{u})} $$we get alloc(u) ∈ P;
-
or l = 0. Then (0, v) ∈ H for some \(v\in \mathbb {N}\). Using characteristic Property P4 we deduce \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \) and:
-
either v = s(x i ) and u ↪ x i ∈ P for some i ∈ [1, q]. As P is closed under the rule
$$\frac{\mathtt{u}\hookrightarrow{\mathtt{x}_{i}}}{\mathtt{alloc}(\mathtt{u})} $$we get alloc(u) ∈ P;
-
or v = 0 and u ↪ u ∈ P and \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \). As P is closed under the rule
$$\frac{\mathtt{u}\hookrightarrow\mathtt{u}}{\mathtt{alloc}(\mathtt{u})} $$we get alloc(u) ∈ P;
-
or v = 2q + 1and alloc(u) ∈ P and \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}},\mathtt {u} \hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \);
-
Now let us assume alloc(u) ∈ P and let us show (s, h) ⊧ l alloc(u). We have three cases for l ∈ L:
-
either l = s(x i ) with x i = u ∈ P for some i ∈ [1, q]. As P is closed under the rules
$$\frac{\mathtt{x}_{i}=\mathtt{u}}{\mathtt{u}=\mathtt{x}_{i}}\qquad \frac{\mathtt{u}=\mathtt{x}_{i}\quad \mathtt{alloc}(\mathtt{u})}{\mathtt{conv}(\mathtt{x}_{i},\mathtt{x}_{i})} $$we get conv(x i , x i ) ∈ P and thus (s, h) ⊧ l conv(x i , x i ) from the earlier case B = conv(x i , x i ). Hence l = s(x i ) ∈ dom(h) and we deduce (s, h) ⊧ l alloc(u);
-
or \( l=\mathfrak {h}_{i}\) with x i ↪ u ∈ P and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}\}\cap \text {\textsf {P}}=\varnothing \). As P is closed under the rules
$$\frac{\mathtt{x}_{i}\hookrightarrow\mathtt{u}\quad\mathtt{alloc}(\mathtt{u})}{\mathtt{toalloc}(\mathtt{x}_{i})} $$we get toalloc(x i ) ∈ P. We derive (s, h) ⊧ l x i ↪ u (from the earlier case B = x i ↪ u) and (s, h) ⊧ l toalloc(x i ) (from the earlier case B = toalloc(x i )). Thus we get (s, h) ⊧ l alloc(u);
-
or l = 0 and \(\{{\mathtt {x}_{1}}={\mathtt {u}},\ldots ,{\mathtt {x}_{q}}={\mathtt {u}}, {\mathtt {x}_{1}}\hookrightarrow \mathtt {u},\ldots ,{\mathtt {x}_{q}}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \). We consider three cases:
-
either u ↪ x i ∈ P holds for some i ∈ [1, q]. In this case, (0, s(x i )) ∈ H by definition of H and we get (s, h) ⊧ l alloc(u);
-
or \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}\}\cap \text {\textsf {P}}=\varnothing \) and u ↪ u ∈ P. In this case, (0, 0) ∈ H by definition of H and we get (s, h) ⊧ l alloc(u);
-
or \(\{\mathtt {u}\hookrightarrow {\mathtt {x}_{1}},\ldots ,\mathtt {u}\hookrightarrow {\mathtt {x}_{q}}, \mathtt {u}\hookrightarrow \mathtt {u}\}\cap \text {\textsf {P}}=\varnothing \). In that case (0, 2q + 1) ∈ H by definition of H and we get (s, h)⊧ l alloc(u).
-
-
□
The next proposition is exclusively used in the proof of upcoming Proposition 5.5.
Proposition D.1
Let \(q\geqslant 1\). Let s be a store, h 1 and h 2 be two heaps and l be a location. We assume that \(\heartsuit (s , h_{1})\cup \{ l \}=\heartsuit (s , h_{2})\cup \{ l \}\) and that h 1 and h 2 are identical maps on that subset of locations. Then (s, h 1, l) ≃ b (s, h 2, l).
Proof
Let us denote \(D=\heartsuit (s,h_{1})\cup \{ l\}=\heartsuit (s,h_{2})\cup \{ l\}\). We show that (s, h 1) ⊧ l B implies (s, h 2) ⊧ l B by case analysis on B:
- B is x i = x j ::
-
if (s, h 1) ⊧ l x i = x j then s(x i ) = s(x j ) and thus (s, h 2) ⊧ l x i = x j ;
- B is x i ↪ x j ::
-
if (s, h 1) ⊧ l x i ↪ x j then h 1(s(x i )) = s(x j ). Hence \( s(\mathtt {x}_{i})\in \text {ref}(s,h_{1})\subseteq D\) and we deduce h 2(s(x i )) = h 1(s(x i )) = s( j ). We conclude (s, h 2) ⊧ l x i ↪ x j ;
- B is conv(x i , x j )::
-
if (s, h 1) ⊧ l conv(x i , x j ) then h 1(s(x i )) = h 1(s(x j )). Hence we have the inclusion \(\{ s(\mathtt {x}_{i}), s(\mathtt {x}_{j})\}\subseteq D\) and we deduce h 2(s(x i )) = h 1(s(x i )) = h 1(s(x j )) = h 2(s(x j )). We conclude (s, h 2) ⊧ l conv(x i , x j );
- B is btwn(x i , x j )::
-
if (s, h 1) ⊧ l btwn(x i , x j ) then h 1(h 1(s(x i ))) = s(x j ). Hence \(\{ s(\mathtt {x}_{i}), h_{1}(s(\mathtt {x}_{i}))\}\subseteq D\) and we deduce h 2(h 2(s(x i ))) = h 2(h 1(s(x i ))) = h 1(h 1(s(x i ))) = s( j ). We conclude (s, h 2) ⊧ l btwn(x i , x j );
- B is toalloc(x i )::
-
if (s, h 1) ⊧ l toalloc(x i ) then h 1(s(x i )) ∈ dom(h 1). Hence \(\{ s(\mathtt {x}_{i}), h_{1}(s(\mathtt {x}_{i}))\}\subseteq D\). Then h 1 and h 2 have the same value at s(x i ) hence h 2(s(x i )) = h 1(s(x i )) = u. But h 1 and h 2 must also have the same value on u ∈ D, hence h 2(u) must be defined (and equal to h 1(u)) and we deduce h 2(s(x i )) = u ∈ dom(h 2). We conclude (s, h 2) ⊧ l toalloc(x i );
- B is toloop(x i )::
-
if (s, h 1) ⊧ l toloop(x i ) then h 1(h 1(s(x i ))) = h 1(s(x i )). Hence \(\{ s(\mathtt {x}_{i}), h_{1}(s(\mathtt {x}_{i}))\}\subseteq D\). We deduce h 2(h 2(s(x i ))) = h 2(h 1(s(x i ))) = h 1(h 1(s(x i ))) = h 1(s(x i )) = h 2(s(x i )). We conclude (s, h 2) ⊧ l toloop(x i );
- B is u ↪ u::
-
if (s, h 1) ⊧ l u ↪ u then h 1(l) = l. As l ∈ D, we deduce h 2(l) = h 1(l) = l and we conclude (s, h 2) ⊧ l u ↪ u;
- B is alloc(u)::
-
if (s, h 1) ⊧ l alloc(u) then l ∈ dom(h 1). As l ∈ D, we deduce l ∈ dom(h 2) and we conclude (s, h 2) ⊧ l alloc(u);
- B is x i = u::
-
if (s, h 1) ⊧ l x i = u then s(x i ) = l and we conclude (s, h 2) ⊧ l x i = u;
- B is x i ↪ u::
-
if (s, h 1) ⊧ l x i ↪ u then h 1(s(x i )) = l. Then s(x i ) ∈ D and we get h 2(s(x i )) = h 1(s(x i )) = l. We conclude (s, h 2) ⊧ l x i ↪ u;
- B is u ↪ x i ::
-
if (s, h 1) ⊧ l ↪ x i then h 1(l) = s(x i ). As l ∈ D, we deduce h 2(l) = h 1(l) = s(x i ) and we conclude (s, h 2) ⊧ l u ↪ x i .
□
Proposition 5.5
Let \(q\geqslant 1\). Let \( s :\mathcal {V}\rightarrow \mathbb {N}\) be a store, \( h :\mathbb {N}\rightharpoondown \mathbb {N}\) be a heap and \( l \in \mathbb {N}\) be a location. Let (p 1,…,p q , l, r) be a cardinality assignment such that:
-
1.
s(x i ) = s(x j ) implies p i = p j for all i, j ∈ [1, q];
-
2.
\(\text {card}(\text {pred}_{\overline {\heartsuit }}(s , h ,i))\leqslant \text {\textsf {p}}_{i}\) for any i ∈ [1, q];
-
3.
\(\text {card}(\text {loop}_{\overline {\heartsuit }}(s, h))\leqslant \text {\textsf {l}}\) ;
-
4.
\(\text {card}(\text {rem}_{\overline {\heartsuit }}(s, h))\leqslant \text {\textsf {r}}\).
There exists a heap \( h^{\prime }\) such that:
-
\((s,h,l)\simeq _{b}(s,h^{\prime },l)\) ;
-
\(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i))= \text {\textsf {p}}_{i}\) for any i ∈ [1, q];
-
\(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))= \text {\textsf {l}}\) ;
-
\(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))= \text {\textsf {r}}\).
Proof
Let us define \(\underline {i}=\min \{j\in [1,q]\mid s(\mathtt {x}_{i})= s(\mathtt {x}_{j})\}\) for every i ∈ [1, q], m = maxval(s, h, l), \(n=\max \{\text {\textsf {p}}_{1},\ldots ,\text {\textsf {p}}_{q},\text {\textsf {l}},\text {\textsf {r}}\}\), \(\text {\textsf {p}}^{\prime }_{i}=\text {\textsf {p}}_{i}-\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,i))\) for every i ∈ [1, q], \(\text {\textsf {l}}^{\prime } = \text {\textsf {l}} - \text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))\) and \(\text {\textsf {r}}^{\prime } = \text {\textsf {r}} - \text {card}(\text {rem}_{\overline {\heartsuit }}(s,h))\). We define \( h^{\prime }\) by the following rules:
-
\(h^{\prime }(u)=v\) when \(u\leqslant m\) and h(u) = v;
-
\(h^{\prime }(u)=v\) when \(u=m+2+\underline {i}.n+d\), v = s( i ), i ∈ [1, q], \(1\leqslant d \leqslant \text {\textsf {p}}^{\prime }_{i}\);
-
\(h^{\prime }(u)=v\) when u = m + 2 + (q + 1).n + d, v = u and \(1\leqslant d \leqslant \text {\textsf {l}}^{\prime }\);
-
\(h^{\prime }(u)=v\) when u = m + 2 + (q + 2).n + d, v = m + 1 and \(1\leqslant d \leqslant \text {\textsf {r}}^{\prime }\).
Then it is easy to check that \( h^{\prime }\) is a heap that satisfies the following properties:
-
\(\heartsuit (s,h^{\prime })=\heartsuit (s,h)\) and thus \(\heartsuit (s,h^{\prime })\cup \{ l\}=\heartsuit (s,h)\cup \{ l\}\);
-
the restrictions of h and \( h^{\prime }\) to \(\heartsuit (s,h)\cup \{ l\}\) are identical maps;
-
\(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i)=\text {pred}_{\overline {\heartsuit }}(s,h,i)\uplus [{m+2+\underline {i}.n+1},{m+2+\underline {i}.n+\text {\textsf {p}}^{\prime }_{i}}]\);
-
\(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime })=\text {loop}_{\overline {\heartsuit }}(s,h)\uplus [{m+2+(q+2).n+1},{m+2+(q+2).n+\text {\textsf {l}}^{\prime }}]\);
-
\(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime })=\text {rem}_{\overline {\heartsuit }}(s,h)\uplus [{m+2+(q+2).n+1},{m+2+(q+2).n+\text {\textsf {r}}^{\prime }}]\).
Hence the identities \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i))=\text {\textsf {p}}_{i}\) for i ∈ [1, q], \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}\) are obvious. The basic equivalence \((s,h,l)\simeq _{b}(s,h^{\prime },l)\) comes from Proposition D.1 (see Appendix D). □
Proposition 5.7
If the conjunction of the formulæ contained in \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable then the triple (B +, B −, S) is n-consistent for any n ∈ {1, 2, 3}.
Proof
Let us first prove the result for 1-consistency. Let us fix a triple (B +, B −, S) and consider a memory state (s, h) and a location l such all the formulæ in \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l). Let us show that Conditions C1.1 to C1.4 hold:
- C1.1:
-
no formula in B − is satisfied in (s, h, l) and by Proposition 5.1, all the formulæ of cl(B +) are satisfied in (s, h, l). Hence we deduce \(\text {\textsf {B}}^{-}\cap \text {cl}(\text {\textsf {B}}^{+})=\varnothing \);
- C1.2:
-
if \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\) and \(\{\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant a,\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant b\}\subseteq \text {\textsf {S}}\) then we deduce s(x i ) = s(x j ), \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,i))\geqslant a\) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))< b\). But from s(x i ) = s(x j ) we get \(\text {pred}_{\overline {\heartsuit }}(s,h,i)=\text {pred}_{\overline {\heartsuit }}(s,h,j)\) hence a < b;
- C1.3:
-
if \(\{\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a,\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant b\}\subseteq \text {\textsf {S}}\) then \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))\geqslant a\) and \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))<b\) both hold hence a < b;
- C1.4:
-
if \(\{\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a,\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant b\}\subseteq \text {\textsf {S}}\) then \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h))\geqslant a\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h))<b\) both hold hence a < b.
Let us prove the result for 2-consistency. Let us fix a triple (B +, B −, S). Let us consider amemory state (s, h) and alocation l such that all the formulæ in \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l). We have already established that (B +, B −, S) is 1-consistent in this case. Let us show that Conditions C2.1 and C2.2 hold.
- C2.1:
-
if \(\{{\mathtt {x}_{i}}={\mathtt {x}_{j}},\mathtt {u}\hookrightarrow {\mathtt {x}_{i}}\}\subseteq \text {cl}(\text {\textsf {B}}^{+})\) and \(\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant 1\in \text {\textsf {S}}\) then we deduce s(x i ) = s(x j ), h(l) = s(x i ) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))< 1\). But then h(l) = s(x j ) hence l ∈ pred(s, h, j). From \(\text {pred}_{\overline {\heartsuit }}(s,h,j)=\varnothing \) we derive l ∈ pred♡(s, h, j) hence \( l\in \heartsuit (s,h)\subseteq s(\mathcal {V})\cup h(s(\mathcal {V}))\). Hence (s, h, l) satisfies at least one formula B of \(\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\). We deduce that all the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l) hence \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 1-consistent;
- C2.2:
-
if u ↪ u ∈ cl(B +) and \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant 1\in \text {\textsf {S}}\) then we have h(l) = l and \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))< 1\). From \(\text {loop}_{\overline {\heartsuit }}(s,h)=\varnothing \) and l ∈ loop♡(s, h) we deduce \( l\in \heartsuit (s,h)\subseteq s(\mathcal {V})\cup h(s(\mathcal {V}))\). Hence (s, h, l) satisfies at least one formula B of \(\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\). We deduce that all the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l) hence \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 1-consistent;
Let us prove the result for 3-consistency. Let us fix a triple (B +, B −, S) and consider a memory state (s, h) and a location l such all the formulæin \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l). We have already established that (B +, B −, S) is 2-consistent in this case. Let us show that Condition C3.1 holds:
- C3.1:
-
if alloc(u) ∈ cl(P) and \(\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant 1\in \text {\textsf {S}}\) then l ∈ dom(h) and \(\text {rem}_{\overline {\heartsuit }}(s,h)=\varnothing \). Hence using Lemma 2.6, either l ∈ ♡(s, h)or \( l\in \text {pred}_{\overline {\heartsuit }}(s,h,i)\) for some i ∈ [1, q] or \( l\in \text {loop}_{\overline {\heartsuit }}(s,h)\). As a consequence, (s, h, l) satisfies at least one formula B of \(\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\cup \text {\textsf {Fm}}_{\mathtt {u}}\cup \{\mathtt {u} \hookrightarrow \mathtt {u}\}\). We deduce that all the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) are satisfied in (s, h, l) hence the triple \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 2-consistent.
□
Proposition 5.8
If the triple (B +, B −, S) is 3-consistent then the conjunction of the formulæ in \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable.
Proof
Let us first consider the case where (B +, B −, S) is 1-consistent (which is the weakest of the assumptions of 1-, 2- or 3-consistency). We define a cardinality assignment (p 1,…,p q , l, r) by:
where we assume \(\max (\varnothing )=0\). Since (B +, B −, S) is 1-consistent, we check that the following properties hold for any \(a\in \mathbb {N}\) and all i, j ∈ [1, q]:
- Property (P0):
-
let us assume \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\) and let us show \(\text {\textsf {p}}_{i}\leqslant \text {\textsf {p}}_{j}\). Let \(a\in \mathbb {N}\) and k ∈ [1, q] be such that \({\mathtt {x}_{i}}={\mathtt {x}_{k}}\in \text {cl}(\text {\textsf {B}}^{+})\) and \(\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{k})\geqslant a\in \text {\textsf {S}}\). Let us show \(a\leqslant \text {\textsf {p}}_{j}\). Since cl(B +) is closed under rules
$$\frac{\mathtt{x}_{i}=\mathtt{x}_{j}}{\mathtt{x}_{j}=\mathtt{x}_{i}}\qquad\frac{\mathtt{x}_{j}=\mathtt{x}_{i} \quad\mathtt{x}_{i}=\mathtt{x}_{k}}{\mathtt{x}_{j}=\mathtt{x}_{k}} $$we deduce \({\mathtt {x}_{j}}={\mathtt {x}_{k}}\in \text {cl}(\text {\textsf {B}}^{+})\). Hence by definition of p j (\(\max \)), we get \(a\leqslant \text {\textsf {p}}_{j}\). We conclude \(\text {\textsf {p}}_{i}\leqslant \text {\textsf {p}}_{j}\). The relation \(\text {\textsf {p}}_{j}\leqslant \text {\textsf {p}}_{i}\) is derived directly because \({\mathtt {x}_{j}}={\mathtt {x}_{i}}\in \text {cl}(\text {\textsf {B}}^{+})\) holds as well;
- Property (P1):
-
if \(\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant a\in \text {\textsf {S}}\) then, as cl(B +) is closed under rule
$$\frac{}{\mathtt{x}_{i}=\mathtt{x}_{i}}$$we deduce \({\mathtt {x}_{i}}={\mathtt {x}_{i}}\in \text {cl}(\text {\textsf {B}}^{+})\) and thus \(a\leqslant \text {\textsf {p}}_{i}\) by definition of p i ;
- Property (P2):
-
let us assume \(\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant a\in \text {\textsf {S}}\) and let us show p i < a. Hence, let \(b\in \mathbb {N}\) and k ∈ [1,q] be such that \({\mathtt {x}_{i}}={\mathtt {x}_{k}}\in \text {cl}(\text {\textsf {B}}^{+})\) and \(\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{k})\geqslant b \in \text {\textsf {S}}\) and let us show b < a. From \({\mathtt {x}_{i}}={\mathtt {x}_{k}}\in \text {cl}(\text {\textsf {B}}^{+})\) we deduce \({\mathtt {x}_{k}}={\mathtt {x}_{i}}\in \text {cl}(\text {\textsf {B}}^{+})\). As we also have \(\{\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{k})\geqslant b,\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{i})\geqslant a\}\subseteq \text {\textsf {S}}\), by Property C1.2 (which holds for 1-consistency) we deduce b < a. We conclude p i < a;
- Property (P3):
-
if \(\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by definition of l we have \(a\leqslant \text {\textsf {l}}\);
- Property (P4):
-
let us assume \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) and let us show l < a. Hence, let \(b\in \mathbb {N}\) be s.t. \(\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant b\in \text {\textsf {S}}\) and let us show b < a. We have \(\{\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant b,\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\}\subseteq \text {\textsf {S}}\) hence by Property C1.3 we deduce b < a. We conclude l < a;
- Property (P5):
-
if \(\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by definition of r we have \(a\leqslant \text {\textsf {r}}\);
- Property (P6):
-
let us assume \(\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) and let us show r < a. Hence, let \(b\in \mathbb {N}\) be such that \(\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant b\in \text {\textsf {S}}\) and let us show b < a. We have \(\{\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant b,\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\}\subseteq \text {\textsf {S}}\)hence by PropertyC1.4 we deduce b < a.We conclude r < a.
From Property (P0), we deduce that in the pre-canonical model (s, h, l) of cl(B +), if s(x i ) = s(x j ) then p i = p j by Proposition 5.3.
Now we show that the conjunction of the formulæ in \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable if one of following properties hold:
- (S1):
-
(B +, B −, S) is 1-consistent and either alloc(u) ∉ cl(B +) or \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \);
- (S2):
-
(B +, B −, S) is 2-consistent and \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\cup \text {\textsf {Fm}}_{\mathtt {u}}\cup \{\mathtt {u} \hookrightarrow \mathtt {u}\})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \);
- (S3):
-
(B +, B −, S) is 3-consistent.
Let us show (S1). We assume that (B +, B −, S) is 1-consistent and either alloc(u) ∉ cl(B +) or \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \) hold, and we show that \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. We consider the canonical pre-model (s, h, l) of cl(B +); see Proposition 5.3. If alloc(u) ∉ cl(B +) holds then l ∉ dom(h); and if \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \) holds then \( l\in \mathfrak {p}\heartsuit (s,h)\). As \(\text {dom}(h)\subseteq \heartsuit (s,h)\cup \{ l\}\), under any of the two hypothesis alloc(u) ∉ cl(B +) or \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \) we have \(\text {dom}(h)\subseteq \heartsuit (s,h)\). Hence \(\text {pred}_{\overline {\heartsuit }}(s,h,i)=\text {loop}_{\overline {\heartsuit }}(s,h)= \text {rem}_{\overline {\heartsuit }}(s,h)=\varnothing \) for any i ∈ [1, q]. Using Proposition 5.5 with Property (P0), there exists a heap \( h^{\prime }\) such that \((s,h,l)\simeq _{b}(s,h^{\prime },l)\) and \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i))=\text {\textsf {p}}_{i}\), \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}\). By Properties (P1–6), we derive that \((s,h^{\prime },l)\) satisfies all the formulæ of S. For instance, if \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by (P4) we have \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}} < a\) and thus \((s,h^{\prime })\models _{l}\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\). From \((s,h,l)\simeq _{b}(s,h^{\prime },l)\), \(\text {\textsf {B}}^{-}\cap \text {cl}(\text {\textsf {B}}^{+})=\varnothing \) and Proposition 5.3, we deduce that \((s,h^{\prime },l)\) satisfies all the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\). Hence the conjunction of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable.
Let us show (S2). We assume that (B +, B −, S) is 2-consistent and \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\cup \text {\textsf {Fm}}_{\mathtt {u}}\cup \{\mathtt {u} \hookrightarrow \mathtt {u}\})\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \) and we show that \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. We can further assume that alloc(u) ∈ cl(B +) and \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}})\cap \text {cl}(\text {\textsf {B}}^{+})=\varnothing \) because otherwise, as (B +, B −, S) is 1-consistent, by Property (S1) we already have that \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. Hence we have either \(\text {\textsf {Fm}}_{\mathtt {u}}\cap \text {cl}(\text {\textsf {B}}^{+})\neq \varnothing \) or u ↪ u ∈ cl(B +):
-
if \(\mathtt {u}\hookrightarrow {\mathtt {x}_{i}}\in \text {cl}(\text {\textsf {B}}^{+})\) for some i ∈ [1, q]. In the canonical pre-model (s, h, l) of cl(B +), we have \( l\in \text {pred}_{\overline {\heartsuit }}(s,h,i)\). But since \(\text {dom}(h)\subseteq \heartsuit (s,h)\cup \{ l\}\), we deduce \(\text {pred}_{\overline {\heartsuit }}(s,h,j)=\{ l\}\) if s(x i ) = s(x j ), \(\text {pred}_{\overline {\heartsuit }}(s,h,j)=\varnothing \) if s(x i ) ≠ s(x j ) and \(\text {loop}_{\overline {\heartsuit }}(s,h)=\text {rem}_{\overline {\heartsuit }}(s,h)=\varnothing \). We consider two sub-cases depending on \(\{\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant 1\mid {\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\}\cap \text {\textsf {S}}\):
-
if \(\{\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant 1\mid {\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\}\cap \text {\textsf {S}}=\varnothing \). Then let us define a new cardinality assignment \((\text {\textsf {p}}^{\prime }_{1},\ldots ,\text {\textsf {p}}^{\prime }_{q},\text {\textsf {l}},\text {\textsf {r}})\) by \(\text {\textsf {p}}^{\prime }_{j}=\max (1,\text {\textsf {p}}_{j})\) if \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\), \(\text {\textsf {p}}^{\prime }_{j}=\text {\textsf {p}}_{j}\) if \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\not \in \text {cl}(\text {\textsf {B}}^{+})\). Let us show that \((\text {\textsf {p}}^{\prime }_{1},\ldots ,\text {\textsf {p}}^{\prime }_{q},\text {\textsf {l}},\text {\textsf {r}})\) satisfies the requirements of Proposition 5.5 for the canonical pre-model (s, h, l) of cl(B +): s(x j ) = s(x k ) implies \({\mathtt {x}_{j}}={\mathtt {x}_{k}}\in \text {cl}(\text {\textsf {B}}^{+})\)implies p j =p k implies \(\text {\textsf {p}}^{\prime }_{j}=\text {\textsf {p}}^{\prime }_{k}\) for any j, k ∈ [1,q]; if \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\) then \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))=1\leqslant \max (1,\text {\textsf {p}}_{j})=\text {\textsf {p}}^{\prime }_{j}\); if \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\not \in \text {cl}(\text {\textsf {B}}^{+})\) then \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h,j))=0\leqslant \text {\textsf {p}}^{\prime }_{j}\); \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h))=0\leqslant \text {\textsf {l}}\); and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h))=0\leqslant \text {\textsf {r}}\).
Using the cardinality assignment \((\text {\textsf {p}}^{\prime }_{1},\ldots ,\text {\textsf {p}}^{\prime }_{q},\text {\textsf {l}},\text {\textsf {r}})\), we extend the canonical pre-model (s, h, l) of cl(B +) using Proposition 5.5 and we get a heap \(h^{\prime }\) s.t. \((s,h,l)\simeq _{b}(s,h^{\prime },l)\), \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },j))=\max (1,\text {\textsf {p}}_{j})\) if s(x i ) = s(x j ), \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },j))=\text {\textsf {p}}_{j}\) if s(x i ) ≠ s(x j ), \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}\). From the equivalence \((s,h,l)\simeq _{b}(s,h^{\prime },l)\) we deduce that \((s,h^{\prime },l)\) satisfies all the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\). Let us check that \((s,h^{\prime },l)\) satisfies the formulæ of S:
-
if \(\#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant a\in \text {\textsf {S}}\) then by Property (P1) we have \(a\leqslant \text {\textsf {p}}_{j}\leqslant \text {\textsf {p}}^{\prime }_{j}= \text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },j))\), hence \((s,h^{\prime })\models _{l} \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant a\);
-
if \(\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant a\in \text {\textsf {S}}\) then either \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\) in which case a > 1 and thus we have \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },j))=\max (1,\text {\textsf {p}}_{j})<a\) by Property (P2), or \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\not \in \text {cl}(\text {\textsf {B}}^{+})\) in which case \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },j))=\text {\textsf {p}}_{j}<a\) by Property (P2). In any case we have \((s,h^{\prime })\models _{l} \neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant a\);
-
if \(\#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by Property (P3) we derive \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}\geqslant a\), hence \((s,h^{\prime })\models _{l} \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\);
-
if \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by Property (P4) we derive \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}< a\), hence \((s,h^{\prime })\models _{l} \neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant a\);
-
if \(\#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by Property (P5) we get \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}\geqslant a\), hence \((s,h^{\prime })\models _{l} \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\);
-
if \(\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\in \text {\textsf {S}}\) then by Property (P6) we derive \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}< a\), hence \((s,h^{\prime })\models _{l} \neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant a\);
We deduce that \((s,h^{\prime },l)\) satisfies the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\);
-
-
if \(\{\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant 1\mid {\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\}\cap \text {\textsf {S}}\neq \varnothing \). Then there exists some j ∈ [1, q] such that \(\neg \#\mathtt {pred}_{\overline {\heartsuit }}(\mathtt {x}_{j})\geqslant 1\in \text {\textsf {S}}\) and \({\mathtt {x}_{i}}={\mathtt {x}_{j}}\in \text {cl}(\text {\textsf {B}}^{+})\). Then by Condition C2.1, \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 1-consistent for some \( B\in \text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\). By Property (S1), we deduce that the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. Hence the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable as well;
-
-
if u ↪ u ∈ cl(B +). In the canonical pre-model of cl(B +), we have \(\text {pred}_{\overline {\heartsuit }}(s,h,i)=\text {rem}_{\overline {\heartsuit }}(s,h)=\varnothing \) for any i ∈ [1, q] and \(\text {loop}_{\overline {\heartsuit }}(s,h)=\{ l\}\). We consider two sub-cases:
-
either \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant 1\not \in \text {\textsf {S}}\). As earlier, we extend the canonical pre-model (s, h, l) under the cardinality assignment \((\text {\textsf {p}}_{1},\ldots ,\text {\textsf {p}}_{q},\max (1,\text {\textsf {l}}),\text {\textsf {r}})\) using Proposition 5.5 and we get a heap \( h^{\prime }\) such that \((s,h,l)\simeq _{b}(s,h^{\prime },l)\), \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i))=\text {\textsf {p}}_{j}\) for any i ∈ [1, q], \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\max (1,\text {\textsf {l}})\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {r}}\). We can then show that \((s,h^{\prime },l)\) satisfies the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\);
-
or \(\neg \#\mathtt {loop}_{\overline {\heartsuit }}\geqslant 1\in \text {\textsf {S}}\). Then by Condition C2.2, \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 1-consistent for some \( B\in \text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\). By Property (S1), we deduce that the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. Hence the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable as well.
-
Let us finally show (S3). We assume that (B +, B −, S) is 3-consistent and we prove that the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. We further assume that alloc(u) ∈ cl(B +) and \((\text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\cup \text {\textsf {Fm}}_{\mathtt {u}}\cup \{\mathtt {u} \hookrightarrow \mathtt {u}\})\cap \text {cl}(\text {\textsf {B}}^{+})=\varnothing \) because otherwise we can either apply Property (S1) or Property (S2). Hence in the canonical pre-model (s, h, l) of cl(B +), we have \( l\in \text {rem}_{\overline {\heartsuit }}(s,h)\). But since \(\text {dom}(h)\subseteq \heartsuit (s,h)\cup \{ l\}\), we deduce \(\text {pred}_{\overline {\heartsuit }}(s,h,i)=\varnothing \) for any i ∈ [1,q], \(\text {loop}_{\overline {\heartsuit }}(s,h)=\varnothing \) and \(\text {rem}_{\overline {\heartsuit }}(s,h)=\{ l\}\). We consider two cases:
-
either \(\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant 1\not \in \text {\textsf {S}}\). As earlier, we extend the canonical model (s, h, l) under the cardinal assignment \((\text {\textsf {p}}_{1},\ldots ,\text {\textsf {p}}_{q},\text {\textsf {l}},\max (1,\text {\textsf {r}}))\) using Proposition 5.5 and we get a heap \(h^{\prime }\) such that \((s,h,l)\simeq _{b}(s,h^{\prime },l)\), \(\text {card}(\text {pred}_{\overline {\heartsuit }}(s,h^{\prime },i))=\text {\textsf {p}}_{i}\) for any i ∈ [1, q], \(\text {card}(\text {loop}_{\overline {\heartsuit }}(s,h^{\prime }))=\text {\textsf {l}}\) and \(\text {card}(\text {rem}_{\overline {\heartsuit }}(s,h^{\prime }))=\max (1,\text {\textsf {r}})\). We deduce that \((s,h^{\prime },l)\) satisfies the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\);
-
or \(\neg \#\mathtt {rem}_{\overline {\heartsuit }}\geqslant 1\in \text {\textsf {S}}\). Then by Condition C3.1, \((\text {\textsf {B}}^{+}\cup \{ B\},\text {\textsf {B}}^{-},\text {\textsf {S}})\) is 2-consistent for some \(B\in \text {\textsf {Eq}}_{\mathtt {u}}\cup \text {\textsf {To}}_{\mathtt {u}}\cup \text {\textsf {Fm}}_{\mathtt {u}}\cup \{\mathtt {u} \hookrightarrow \mathtt {u}\}\). By Property (S2), we deduce that the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \{ B\}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable. Hence the conjunction of the formulæ of \(\text {\textsf {B}}^{+}\cup \neg \text {\textsf {B}}^{-}\cup \text {\textsf {S}}\) is satisfiable as well.
□
Rights and permissions
About this article
Cite this article
Demri, S., Galmiche, D., Larchey-Wendling, D. et al. Separation Logic with One Quantified Variable. Theory Comput Syst 61, 371–461 (2017). https://doi.org/10.1007/s00224-016-9713-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00224-016-9713-1



 . Then, by Proposition 2.24 applied to α and L
0, we chooseL and
. Then, by Proposition 2.24 applied to α and L
0, we chooseL and 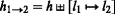 and
and 
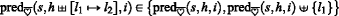
 . We also have
. We also have  . As
. As  . As
. As  ;
; ;
; .
.
 ;
; .
. by
by  and
and  and we deduce
and we deduce  holds, we get (s, h) ⊧
l
A
1 ∗ A
2.
holds, we get (s, h) ⊧
l
A
1 ∗ A
2. and (s, h
2) ⊧
l
A
2. For each c ∈ {1, 2}, from
and (s, h
2) ⊧
l
A
2. For each c ∈ {1, 2}, from  . We have
. We have
 . The relations
. The relations 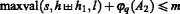 maxval and thus we have
maxval and thus we have 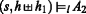 by induction hypothesis.
by induction hypothesis. . So we assume h
1 ⊥ h and
. So we assume h
1 ⊥ h and
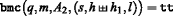 . We have
. We have  . We have
. We have 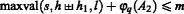 maxval and thus we get
maxval and thus we get  from the induction hypothesis.
from the induction hypothesis.