Abstract
We show that the canonical bases in  and the Schur algebra are compatible; in fact we extend this result to p-canonical bases. This follows immediately from a fullness result for a functor categorifying this map. In order to prove this result, we also explain the connections between categorifications of the Schur algebra which arise from parity sheaves on partial ag varieties, singular Soergel bimodules and Khovanov and Lauda's “flag category," which are of some independent interest.
and the Schur algebra are compatible; in fact we extend this result to p-canonical bases. This follows immediately from a fullness result for a functor categorifying this map. In order to prove this result, we also explain the connections between categorifications of the Schur algebra which arise from parity sheaves on partial ag varieties, singular Soergel bimodules and Khovanov and Lauda's “flag category," which are of some independent interest.
Similar content being viewed by others
References
A. A. Beilinson, J. Bernstein, P. Deligne, Faisceaux pervers, in: Analysis and Topology on Singular Spaces, I (Luminy, 1981), Astérisque, Vol. 100, Soc. Math. France, Paris, 1982, pp. 5–171.
A. Beilinson, V. Ginzburg, W. Soergel, Koszul duality patterns in representation theory, J. Amer. Math. Soc. 9 (1996), no. 2, 473–527.
A. Beliakova, A. D. Lauda, Categorified quantum
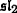 is an inverse limit of flag 2-categories, Transform. Groups 19 (2014), no. 1, 1–26.
is an inverse limit of flag 2-categories, Transform. Groups 19 (2014), no. 1, 1–26.A. A. Beilinson, G. Lusztig, R. MacPherson, A geometric setting for the quantum deformation of GL n , Duke Math. J. 61 (1990), no. 2, 655–677.
J. Brundan, On the definition of Kac–Moody 2-category, arxiv1501.00350 (2015).
S. Cautis, A. D. Lauda, Implicit structure in 2-representations of quantum groups, Selecta Math. (N.S.) 21 (2015), no. 1, 201–244.
B. Elias, M. Khovanov, Diagrammatics for Soergel categories, Int. J. Math. Math. Sci. (2010), Art. ID 978635, 58.
D. Juteau, C. Mautner, G. Williamson, Parity sheaves, J. Amer. Math. Soc. 27 (2014), no. 4, 1169–1212.
M. Khovanov, A. D. Lauda, A categorification of quantum
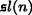 , Quantum Topol. 1 (2010), no. 1, 1–92.
, Quantum Topol. 1 (2010), no. 1, 1–92.M. Khovanov, A. D. Lauda, M. Mackaay, M. Stošić, Extended Graphical Calculus for Categori_ed Quantum FX, Mem. Amer. Math. Soc. 219 (2012), no. 1029.
G. Lusztig, Introduction to Quantum Groups, Progress in Mathematics, Vol. 110, Birkhäuser Boston, Boston, MA, 1993.
M. Mackaay, M. Stošić, P. Vaz, A diagrammatic categorification of the q-Schur algebra, Quantum Topol. 4 (2013), no. 1, 1–75.
R. Rouquier, 2-Kac-Moody algebras, arxiv0812.5023 (2008).
W. Soergel, Corrections for “On the relation between intersection cohomology and representation theory in positive characteristic", http://home.mathematik.uni-freiburg.de/soergel/PReprints/KorrICP.pdf.
W. Soergel, Kategorie
 , perverse Garben und Moduln über den Koinvariantenzur Weylgruppe, J. Amer. Math. Soc. 3 (1990), no. 2, 421–445.
, perverse Garben und Moduln über den Koinvariantenzur Weylgruppe, J. Amer. Math. Soc. 3 (1990), no. 2, 421–445.W. Soergel, The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 429 (1992), 49–74.
W. Soergel, On the relation between intersection cohomology and representation theory in positive characteristic, in: Commutative Algebra, Homological Algebra and Representation Theory (Catania/Genoa/Rome, 1998), J. Pure Appl. Algebra 152 (2000), no. 1–3, 311–335.
O. Schiffmann, E. Vasserot, Geometric construction of the global base of the quantum modified algebra of FX, Transform. Groups 5 (2000), no. 4, 351–360.
B. Webster, Knot invariants and higher representation theory, to appear in the Memoirs of the American Mathematical Society, arxiv1309.3796 (2015).
B. Webster, Canonical bases and higher representation theory, Compos. Math. 151 (2015), no. 1, 121–166.
G. Williamson, Singular Soergel bimodules, http://people.mpim-bonn.mpg.de/geordie/GW-thesis.pdf.
B. Webster, G. Williamson, A geometric model for Hochschild homology of Soergel bimodules, Geom. Topol. 12 (2008), no. 2, 1243–1263.
Author information
Authors and Affiliations
Corresponding author
Additional information
*Supported by the NSF under Grant DMS-1151473 and the Alfred P. Sloan Foundation.
Rights and permissions
About this article
Cite this article
WEBSTER, B. COMPARISON OF CANONICAL BASES FOR SCHUR AND UNIVERSAL ENVELOPING ALGEBRAS. Transformation Groups 22, 869–883 (2017). https://doi.org/10.1007/s00031-016-9409-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00031-016-9409-2




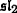 is an inverse limit of flag 2-categories, Transform. Groups 19 (2014), no. 1, 1–26.
is an inverse limit of flag 2-categories, Transform. Groups 19 (2014), no. 1, 1–26.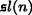 , Quantum Topol. 1 (2010), no. 1, 1–92.
, Quantum Topol. 1 (2010), no. 1, 1–92. , perverse Garben und Moduln über den Koinvariantenzur Weylgruppe, J. Amer. Math. Soc. 3 (1990), no. 2, 421–445.
, perverse Garben und Moduln über den Koinvariantenzur Weylgruppe, J. Amer. Math. Soc. 3 (1990), no. 2, 421–445.