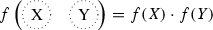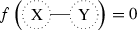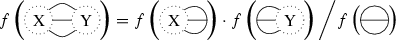Abstract
This is the first paper in a general program to automate skein theoretic arguments. In this paper, we study skein theoretic invariants of planar trivalent graphs. Equivalently, we classify trivalent categories, which are nondegenerate pivotal tensor categories over  generated by a symmetric self-dual simple object X and a rotationally invariant morphism \(1 \rightarrow X \otimes X \otimes X\). Our main result is that the only trivalent categories with \(\dim {\text {Hom}}(1 \rightarrow X^{\otimes n})\) bounded by 1, 0, 1, 1, 4, 11, 40 for \(0 \le n \le 6\) are quantum SO(3), quantum \(G_2\), a one-parameter family of free products of certain Temperley-Lieb categories (which we call ABA categories), and the H3 Haagerup fusion category. We also prove similar results where the map \(1 \rightarrow X^{\otimes 3}\) is not rotationally invariant, and we give a complete classification of nondegenerate braided trivalent categories with dimensions of invariant spaces bounded by the sequence 1, 0, 1, 1, 4. Our main techniques are a new approach to finding skein relations which can be easily automated using Gröbner bases, and evaluation algorithms which use the discharging method developed in the proof of the 4-color theorem.
generated by a symmetric self-dual simple object X and a rotationally invariant morphism \(1 \rightarrow X \otimes X \otimes X\). Our main result is that the only trivalent categories with \(\dim {\text {Hom}}(1 \rightarrow X^{\otimes n})\) bounded by 1, 0, 1, 1, 4, 11, 40 for \(0 \le n \le 6\) are quantum SO(3), quantum \(G_2\), a one-parameter family of free products of certain Temperley-Lieb categories (which we call ABA categories), and the H3 Haagerup fusion category. We also prove similar results where the map \(1 \rightarrow X^{\otimes 3}\) is not rotationally invariant, and we give a complete classification of nondegenerate braided trivalent categories with dimensions of invariant spaces bounded by the sequence 1, 0, 1, 1, 4. Our main techniques are a new approach to finding skein relations which can be easily automated using Gröbner bases, and evaluation algorithms which use the discharging method developed in the proof of the 4-color theorem.


Similar content being viewed by others
Notes
Indeed, N.S. initially did such calculations by hand. Due to human error, this initial version missed the ABA case, but the error was easily caught by the more reliable computer.
In [17] the point \((d,t)=(-1,3/2)\) was not discussed, since in the subfactor context \(d>0\).
Although the computer alerted us to the existence of these relations, we actually computed them by hand, since it is difficult to read off from our computer program where the dots belong. This by-hand calculation following [25] took two people-days.
References
Asaeda M., Haagerup, U.: Exotic subfactors of finite depth with Jones indices \((5+\sqrt{13})/2\) and \((5+\sqrt{17})/2\). Commun. Math. Phys. 202(1), 1–63, (1999). doi:10.1007/s002200050574. arXiv:math.OA/9803044
Bisch, D., Jones, V.F.R.: Singly generated planar algebras of small dimension. Duke Math. J. 101(1), 41–75 (2000). doi:10.1215/ S0012-7094-00-10112-3
Bisch, D., Jones, V.: Singly generated planar algebras of small dimension. II. Adv. Math. 175(2), 297–318 (2003). doi:10.1016/S0001-8708(02)00060-9
Bisch, D., Jones, V.F.R., Liu, Z.: Singly Generated Planar Algebras of Small Dimension, Part III (2014). arXiv:1410.2876
Bigelow, S., Morrison, S., Peters, E., Snyder, N.: Constructing the extended Haagerup planar algebra. Acta Math. 209(1), 29–82 (2012). doi:10.1007/s11511-012-0081-7. arXiv:0909.4099
Barrett, J.W., Westbury, B.W.: Spherical categories. Adv. Math. 143(2), 357–375 (1999). doi:10.1006/aima.1998.1800. arXiv:hep-th/9310164
Clark, S., Wang, W.: Canonical basis for quantum \(\mathfrak{osp}(1\vert 2)\). Lett. Math. Phys. 103(2), 207–231 (2013). doi:10.1007/s11005-012-0592-3. arXiv:1204.3940
Deligne, P.: La série exceptionnelle de groupes de Lie. C. R. Acad. Sci. Paris Sér. I Math 322(4), 321–326 (1996)
Deligne, P.: Catégories tensorielles. Mosc. Math. J. 2(2), 227–248 (2002). (Dedicated to Yuri I. Manin on the occasion of his 65th birthday). http://www.ams.org/distribution/mmj/vol2-2-2002/deligne.pdf
Drinfeld, V., Gelaki, S., Nikshych, D., Ostrik, V.: On braided fusion categories. I. Selecta Math. (N.S.), 16(1), 1–119 (2010). doi:10.1007/s00029-010-0017-z. arXiv:0906.0620
Demillo, R., Lipton, R.: A probabilistic remark on algebraic program testing. Inf. Process. Lett. 7(4), 193–195 (1978)
Evans, D.E., Gannon, T.: The exoticness and realisability of twisted Haagerup-Izumi modular data. Commun. Math. Phys. 307(2), 463–512 (2011). doi:10.1007/s00220-011-1329-3. arXiv:1006.1326
Evans, D.E., Gannon, T.: Near-group fusion categories and their doubles. Adv. Math. 255, 586–640 (2014). doi:10.1016/j.aim.2013.12.014. arXiv:1208.1500
Etingof, P., Gelaki, S., Ostrik, V.: Classification of fusion categories of dimension \(pq\). Int. Math. Res. Not. 2004(57), 3041–3056 (2004). doi:10.1155/S1073792804131206. arXiv:math.QA/0304194
Grossman, P., Izumi, M.: Classification of noncommuting quadrilaterals of factors. Int. J. Math. 19(5), 557–643 (2008). doi:10.1142/S0129167X08004807. arXiv:0704.1121
Grossman, P., Jones, V.F.R.: Intermediate subfactors with no extra structure. J. Am. Math. Soc. 20(1), 219–265 (2007). doi:10.1090/S0894-0347-06-00531-5. arXiv:math/0412423
Grossman, P., Snyder, N.: The Brauer–Picard group of the Asaeda–Haagerup fusion categories. Trans. Am. Math. Soc. (2012). doi:10.1090/tran/6364. arXiv:1202.4396
Grossman, P., Snyder, N.: Quantum subgroups of the Haagerup fusion categories. Commun. Math. Phys. 311(3), 617–643 (2012). doi:10.1007/s00220-012-1427-x. arXiv:1102.2631
Izumi, M., Morrison, S., Penneys, D.: Quotients of \(A_2 * T_2\). 2013. Extended version available as “Fusion categories between \({\cal C} \boxtimes {\cal D}\) and \(\cal C *\cal D\)”. doi:10.4153/CJM-2015-017-4. arXiv:1308.5723
Izumi, M.: A Cuntz algebra approach to the classification of near-group categories. In: Proceedings of the Centre for Mathematics and its Applications (to appear). arXiv:1512.04288
Jaeger, F.: Strongly regular graphs and spin models for the Kauffman polynomial. Geom. Dedic. 44(1), 23–52 (1992)
Jones, V.F.R.: A polynomial invariant for knots via von Neumann algebras. Bull. Am. Math. Soc. (N.S.) 12(1), 103–111 (1985). doi:10.1090/S0273-0979-1985-15304-2
Jones, V.F.R.: Planar algebras I. (1999). arXiv:math.QA/9909027
Kobayashi, K.: Representation theory of \({\rm osp}(1,2)_q\). Z. Phys. C 59(1), 155–158 (1993). doi:10.1007/BF01555850
Kuperberg, G.: The quantum \(G_2\) link invariant. Int. J. Math. 5(1), 61–85 (1994). doi:10.1142/S0129167X94000048. arXiv:math.QA/9201302
Kuperberg, G.: Spiders for rank 2 Lie algebras. Commun. Math. Phys. 180(1), 109–151 (1996). euclid.cmp/1104287237. arXiv:q-alg/9712003
Kuperberg, G.: Jaeger’s Higman-Sims state model and the \(B_2\) spider. J. Algebra 195(2), 487–500 (1997). doi:10.1006/jabr.1997.7045. arXiv:math/9601221
Kazhdan, D., Wenzl, H.: Reconstructing monoidal categories. In: I. M. Gel\(^{^{\prime }}\) fand Seminar, Volume 16 of Advances in Soviet Mathematics, pp. 111–136. American Mathematical Society, Providence, RI (1993) (preview at google books)
Landau, Z.A.: Exchange relation planar algebras. In: Proceedings of the Conference on Geometric and Combinatorial Group Theory, Part II (Haifa, 2000), vol. 95, pp. 183–214 (2002)
Morrison, S., Peters, E., Snyder, N.: Skein theory for the \({\cal D}_{2n}\) planar algebras. J. Pure Appl. Algebra 214(2), 117–139 (2010). doi:10.1016/j.jpaa.2009.04.010. arXiv:0808.0764
Morrison, S., Peters, E., Snyder, N.: Knot polynomial identities and quantum group coincidences. Quantum Topol. 2(2), 101–156 (2011). doi:10.4171/QT/16. arXiv:1003.0022
Morrison, S., Snyder, N.: Subfactors of index less than 5. Part 1: The principal graph odometer. Commun. Math. Phys. 312(1), 1–35 (2012). doi:10.1007/s00220-012-1426-y. arXiv:1007.1730
Newman, M.H.A.: On theories with a combinatorial definition of “equivalence”. Ann. Math. 2(43), 223–243 (1942)
The On-Line Encyclopedia of Integer Sequences. http://oeis.org
Ostrik, V.: Module categories over the Drinfeld double of a finite group. Int. Math. Res. Not. 2003(27), 1507–1520 (2003). doi:10.1155/S1073792803205079. arXiv:math/0202130
Schwartz, J.T.: Fast probabilistic algorithms for verification of polynomial identities. J. Assoc. Comput. Mach. 27(4), 701–717 (1980). doi:10.1145/322217.322225
Secret Blogging Seminar. How to almost prove the 4-color theorem (2009). http://sbseminar.wordpress.com/2009/10/07/how-to-almost-prove-the-4-color-theorem/. Accessed 28 Dec 2014
Siehler, J.: Near-group categories. Algebr. Geom. Topol. 3, 719–775 (2003). doi:10.2140/agt.2003.3.719. arXiv:math/0209073
Speicher, R.: Multiplicative functions on the lattice of noncrossing partitions and free convolution. Math. Ann. 298(4), 611–628 (1994). doi:10.1007/BF01459754
Stanley, R.P.: Enumerative Combinatorics, vol. 2, Volume 62 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (1999). doi:10.1017/CBO9780511609589
Sikora, A.S., Westbury, B.W.: Confluence theory for graphs. Algebr. Geom. Topol. 7, 439–478 (2007). doi:10.2140/agt.2007.7.439. arXiv:math.QA/0609832
Thurston, D.P.: From Dominoes to Hexagons. In: Proceedings of the Centre for Mathematics and its Applications (to appear). arXiv:math/0405482
Thurston, D.P.: The \(F_4\) and \(E_6\) families have a finite number of points (2004). www.math.columbia.edu/~dpt/writing/F4E6.ps
Tuba, I., Wenzl, H.: On braided tensor categories of type \(BCD\). J. Reine Angew. Math. 581:31–69 (2005). doi:10.1515/crll.2005.2005.581.31. arXiv:math.QA/0301142
Vogel, P.: Algebraic structures on modules of diagrams. J. Pure Appl. Algebra 215(6), 1292–1339 (2011). doi:10.1016/j.jpaa.2010.08.013
Zippel, R.: Probabilistic algorithms for sparse polynomials. In: Symbolic and Algebraic Computation (EUROSAM ’79, International Symposium, Marseille, 1979), Volume 72 of Lecture Notes in Computer Science, pp. 216–226. Springer, Berlin (1979)
Acknowledgments
Scott Morrison was supported by an Australian Research Council Discovery Early Career Researcher Award DE120100232, and Discovery Projects DP140100732 and DP160103479. Emily Peters was supported by the NSF Grant DMS-1501116. Noah Snyder was supported by the NSF Grant DMS-1454767. All three authors were supported by DOD-DARPA Grant HR0011-12-1-0009. Scott Morrison would like to thank the Erwin Schrödinger Institute and its 2014 programme on “Modern Trends in Topological Quantum Field Theory” for their hospitality. We would like to thank Greg Kuperberg for a blog comment [37] suggesting applying the discharging method to skein theory, Victor Ostrik for explaining his construction of the twisted Haagerup categories, and David Roe and Dylan Thurston for helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
This is the published version of arXiv:1501.06869.
Appendices
Appendix 1: Skein theoretic invariants and pivotal categories
The goal of this section is to provide background so that this paper is accessible to knot theorists, graph theorists, and other readers unfamiliar with tensor categories or planar algebras.
Suppose we want to study certain numerical invariants f of planar trivalent graphs. Assume that f of the empty diagram is 1, that  and
and  are nonzero, and that f satisfies the following multiplicative conditions:
are nonzero, and that f satisfies the following multiplicative conditions:
-
(0)
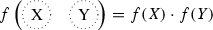
-
(1)
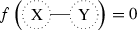
-
(2)

-
(3)
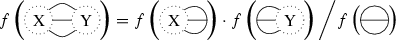
Thus, the invariant of any k-disconnected graph for \(k \le 3\) is determined by the invariants of the pieces.
Example 9.1
An almost trivial example of a multiplicative invariant of graphs is \(a^{\# V}\), for some number a, where \(\# V\) denotes the number of trivalent vertices in the graph.
Example 9.2
An important example of a multiplicative invariant of graphs is the number of n-colorings of the faces of the graph, divided by n. (The division by n is a normalization factor ensuring that the empty graph is assigned 1 instead of n.) This example can be generalized by considering non-integer specializations of the chromatic polynomial.
Question
What examples are there of such multiplicative invariants of trivalent planar graphs?
While the question appears to be an elementary question about planar trivalent graphs, we discover that the examples are actually related to quite distant subjects in mathematics. In particular, we are able to identify each of the small examples we encounter with some surprising or exotic object coming from representation theory or the theory of subfactors!
In order to understand the main results of the paper in the language of graph invariants, we first want to extend this invariant of closed trivalent graphs to an invariant of planar graphs with boundary. That is, we extract a sequence of vector spaces, the ‘open graphs, modulo negligibles.’ We now describe how these vector spaces have the structure of a pivotal tensor category (or planar algebra).
Let  denote the (infinite-dimensional) vector space with basis the planar trivalent graphs drawn in the disk, with n fixed boundary points, up to isotopy rel boundary. This vector space has a natural bilinear pairing, given by gluing two open graphs together (starting at a preferred boundary point), to obtain a closed planar graph, which we then evaluate to a number using our multiplicative invariant f. The kernel of this bilinear pairing is called ‘the negligible elements.’ Let
denote the (infinite-dimensional) vector space with basis the planar trivalent graphs drawn in the disk, with n fixed boundary points, up to isotopy rel boundary. This vector space has a natural bilinear pairing, given by gluing two open graphs together (starting at a preferred boundary point), to obtain a closed planar graph, which we then evaluate to a number using our multiplicative invariant f. The kernel of this bilinear pairing is called ‘the negligible elements.’ Let  denote the quotient vector space of
denote the quotient vector space of  by negligible elements.
by negligible elements.
One may assemble these vector spaces into a single algebraic structure, variously axiomatized as an (unshaded) planar algebra [23], a spider [26] or a pivotal tensor category [6]. We’ll only describe the last in any detail. The category, which we’ll call  , has as objects the natural numbers. We’ll first describe a bigger category of trivalent graphs, which we call
, has as objects the natural numbers. We’ll first describe a bigger category of trivalent graphs, which we call  and which does not depend at all on our multiplicative invariant. In
and which does not depend at all on our multiplicative invariant. In  , the morphisms from n to m are simply the formal linear combinations of planar graphs drawn in a rectangle with n points along the bottom edge and m points along the top edge, i.e., the vector space
, the morphisms from n to m are simply the formal linear combinations of planar graphs drawn in a rectangle with n points along the bottom edge and m points along the top edge, i.e., the vector space  . We can compose morphisms in the obvious way, by stacking rectangles. This category is a tensor category, with the tensor product given by drawing diagrams side by side. Finally, it is a pivotal category, with the evaluation and coevaluation maps given by caps and cups.
. We can compose morphisms in the obvious way, by stacking rectangles. This category is a tensor category, with the tensor product given by drawing diagrams side by side. Finally, it is a pivotal category, with the evaluation and coevaluation maps given by caps and cups.
Inside  , the negligible (with respect to f) elements form a planar ideal—if some (linear combination of) graphs pair with arbitrary other graphs to give zero, then glueing more graph to the boundary preserves this property. We thus define the category
, the negligible (with respect to f) elements form a planar ideal—if some (linear combination of) graphs pair with arbitrary other graphs to give zero, then glueing more graph to the boundary preserves this property. We thus define the category  to be the quotient of
to be the quotient of  by the negligible ideal. This “ideal” property says that we can treat the negligible elements as skein relations: they can be applied locally in any part of a graph. Furthermore, typically this ideal is finitely generated by a few particular skein relations.
by the negligible ideal. This “ideal” property says that we can treat the negligible elements as skein relations: they can be applied locally in any part of a graph. Furthermore, typically this ideal is finitely generated by a few particular skein relations.
Thus, in  , the objects are still the natural numbers and the morphisms from n to m are just
, the objects are still the natural numbers and the morphisms from n to m are just  . The category
. The category  is still a pivotal tensor category, and now it is evaluable (i.e.,
is still a pivotal tensor category, and now it is evaluable (i.e.,  , and in fact
, and in fact  may be identified with the ground field by sending the empty diagram to 1) and non-degenerate (i.e., for every morphism \(x: a \rightarrow b\), there is another morphism \(x': b \rightarrow a\) so
may be identified with the ground field by sending the empty diagram to 1) and non-degenerate (i.e., for every morphism \(x: a \rightarrow b\), there is another morphism \(x': b \rightarrow a\) so  ). Writing X for the generating object in
). Writing X for the generating object in  (i.e., 1 in the natural numbers!), we see that X is a symmetrically self-dual object, with duality pairings and copairings given by the cap and cup diagrams. Moreover, the trivalent vertex is a rotationally symmetric map \(1 \rightarrow X \otimes X \otimes X\).
(i.e., 1 in the natural numbers!), we see that X is a symmetrically self-dual object, with duality pairings and copairings given by the cap and cup diagrams. Moreover, the trivalent vertex is a rotationally symmetric map \(1 \rightarrow X \otimes X \otimes X\).
Example 9.3
If the invariant is the normalized number of n-colorings described in Example 9.2, then a linear combinations of graphs is negligible if and only if for any coloring of the boundary faces the given linear combination of the numbers of ways of extending that coloring to the interior is zero. For example, the following element of  is negligible:
is negligible:

In particular, this gives a skein relation in  which says that you can remove a triangle and multiply by \((n-3)\). There are also other negligible elements; in fact after renormalizing the trivalent vertex,
which says that you can remove a triangle and multiply by \((n-3)\). There are also other negligible elements; in fact after renormalizing the trivalent vertex,  becomes equivalent to the pivotal category \(SO(3)_q\) coming from quantum groups where q is a number satisfying \( (q+q^{-1})^2=n\) (see Sect. 4 for a description of \(SO(3)_q\)).
becomes equivalent to the pivotal category \(SO(3)_q\) coming from quantum groups where q is a number satisfying \( (q+q^{-1})^2=n\) (see Sect. 4 for a description of \(SO(3)_q\)).
Proposition 9.4
The construction of  from f gives a bijective correspondence between trivalent categories and multiplicative invariants of planar graphs.
from f gives a bijective correspondence between trivalent categories and multiplicative invariants of planar graphs.
Proof
First, we prove that the category  constructed from a multiplicative invariant f is trivalent. Consider
constructed from a multiplicative invariant f is trivalent. Consider  . The empty diagram is not negligible, so we need only show that any closed diagram is a multiple of the empty diagram. If \(\alpha \) is a closed diagram and \(\beta \) is the empty diagram, then \(\alpha - f(\alpha ) \beta \) is negligible, so in
. The empty diagram is not negligible, so we need only show that any closed diagram is a multiple of the empty diagram. If \(\alpha \) is a closed diagram and \(\beta \) is the empty diagram, then \(\alpha - f(\alpha ) \beta \) is negligible, so in  we have that \(\alpha = f(\alpha ) \beta \). Now we look at
we have that \(\alpha = f(\alpha ) \beta \). Now we look at  . By multiplicativity, we have that any diagram with one boundary point is negligible, so
. By multiplicativity, we have that any diagram with one boundary point is negligible, so  . The remaining cases are similar.
. The remaining cases are similar.
Given a trivalent category  , we need to construct a multiplicative invariant of planar graphs. The usual diagrammatic calculus for pivotal categories shows that any trivalent category gives an invariant of closed graphs just by interpreting the graphs as elements of
, we need to construct a multiplicative invariant of planar graphs. The usual diagrammatic calculus for pivotal categories shows that any trivalent category gives an invariant of closed graphs just by interpreting the graphs as elements of  and sending the empty diagram to 1.
and sending the empty diagram to 1.
We want to check that this invariant is multiplicative, in which case it is clear that it provides an inverse to  . We first check that the loop and the theta are nonzero. The single strand in
. We first check that the loop and the theta are nonzero. The single strand in  must be nonzero, because if it were zero, then all nonempty diagrams would be zero. Since
must be nonzero, because if it were zero, then all nonempty diagrams would be zero. Since  , we see that any diagram in
, we see that any diagram in  is a multiple of the single strand, hence nondegeneracy says that the inner product of the strand with itself is nonzero, hence the loop value is nonzero. Similarly, by considering
is a multiple of the single strand, hence nondegeneracy says that the inner product of the strand with itself is nonzero, hence the loop value is nonzero. Similarly, by considering  we see that the theta value is nonzero. Next we want to prove the multiplicative properties. Each of these are similar, so we only prove (2). We have that
we see that the theta value is nonzero. Next we want to prove the multiplicative properties. Each of these are similar, so we only prove (2). We have that

is some multiple of the single strand, so we see that  (by pairing with the strand). Substituting this into the LHS of (2) gives the RHS.
(by pairing with the strand). Substituting this into the LHS of (2) gives the RHS.
Appendix 2: Polynomials appearing in determinants
This appendix contains some of the irreducible factors of determinants appearing in this paper. The other irreducible factors, which are very large, are contained in text files packaged with the arXiv source of this paper and described here. Each polynomial is named as \(Q_{i,j}\), where i is the largest exponent of d and j is the largest exponent of t. Where two polynomials have the same pair of largest exponents, we name them with an additional character in the subscript, as in \(Q_{2,4,a}\) and \(Q_{2,4,b}\).
The other factors, \(Q_{7,11}, Q_{8,12}, Q_{11,19}, Q_{21,33}, Q_{22,36}, Q_{51,69}, Q_{54,78}\), and \(Q_{36,60}\) are available in

and Mathematica formats in the polynomials/ subdirectory of the arXiv source as files Q_i,j.tex and Q_i,j.m, and also in the Mathematica notebook code/GroebnerBasisCalculations.nb
Rights and permissions
About this article
Cite this article
Morrison, S., Peters, E. & Snyder, N. Categories generated by a trivalent vertex. Sel. Math. New Ser. 23, 817–868 (2017). https://doi.org/10.1007/s00029-016-0240-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00029-016-0240-3