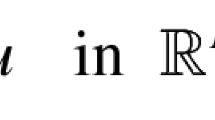Skip to main content
SpringerLink
Log in

Global well-posedness and blow-up solutions of the Cauchy problem for a time-fractional superdiffusion equation

  • Published:
Journal of Evolution Equations Aims and scope Submit manuscript

Abstract

We study the following time-fractional nonlinear superdiffusion equation

$$\begin{aligned} \left\{ \begin{array}{l} {}_0^CD_t^\alpha u-\triangle u=|u|^{p}, \ \ x\in \mathbb {R}^N,\ \ t>0, \\ u(0,x)=u_0(x),\ \ u_t(0,x)=u_1(x),\ \ x\in \mathbb {R}^N, \end{array}\right. \end{aligned}$$

where \(1<\alpha <2\), \(p>1\), \(u_0,u_1\in L^q(\mathbb {R}^N)\) (\(q>1\)) and \({_0^CD_t^\alpha u}\) denotes the Caputo fractional derivative of order \(\alpha .\) The critical exponents of this problem are determined when \(u_1\equiv 0\) and \(u_1\not \equiv 0, \) respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M.F. de Almeida, L.C.F. Ferreira, Self-similarity, symmetries and asymptotic behavior in Morrey spaces for a fractional wave equation, Differ. Integr. Equ. 25 (2012), 957–976.

    MathSciNet  MATH  Google Scholar 

  2. E. Bazhlekova, Fractional evolution equations in Banach spaces, Dissertation, Technische Universiteit Eindhoven, 2001.

  3. C.M. Carracedo, M.S. Alix, The Theory of Fractional Powers of Operators, North-Holland Mathematics Studies, 187 Elsevier, 2001.

  4. P.M. de Carvalho-Neto, G. Planas, Mild solutions to the time fractional Navier-Stokes equations in \(\mathbb{R}^N\), J. Differ. Equ. 259 (2015), 2948–2980.

    Article  MATH  Google Scholar 

  5. T. Cazenave, F. Dickstein and F.B. Weissler, An equation whose Fujita critical exponent is not given by scaling, Nonlinear Anal. 68 (2008), 862–874.

    Article  MathSciNet  MATH  Google Scholar 

  6. P. Clément, S.O. Londen, G. Simonett, Quasilinear evolutionary equations and continuous interpolation spaces, J. Differ. Equ. 196 (2004), 418–447.

    Article  MathSciNet  MATH  Google Scholar 

  7. S.D. Eidelman, A.N. Kochubei, Cauchy problem for fractional diffusion equations, J. Differ. Equ. 199 (2004), 211–255.

    Article  MathSciNet  MATH  Google Scholar 

  8. H. Engler, Asymptotic self-similarity for solutions of partial integro-differential equations, Z. Anal. Anwend. 26 (2007), 417–438.

    Article  MathSciNet  MATH  Google Scholar 

  9. A.Z. Fino, M. Kirane, Qualitative properties of solutions to a time-space fractional evolution equation, Quart. Appl. Math. 70 (2012), 133–157.

    Article  MathSciNet  MATH  Google Scholar 

  10. Y. Fujita, Integrodifferential equation which interpolates the heat equation and the wave equation, Osaka J. Math. 27 (1990), 309–321.

    MathSciNet  MATH  Google Scholar 

  11. Y. Fujita, Integrodifferential equation which interpolates the heat equation and the wave equation II, Osaka J. Math. 27 (1990), 797–804.

    MathSciNet  MATH  Google Scholar 

  12. B. Guo, X. Pu, F. Huang, Fractional Partial Differential Equations and Their Numerical Solutions, World Scientific, 2015.

  13. G. Gripenberg, Weak solutions of hyperbolic-parabolic Volterra equations, Trans. Amer. Math. Soc. 343 (1994), 675–694.

    Article  MathSciNet  MATH  Google Scholar 

  14. H. Hirata, C.X. Miao, Space-time estimates of linear flow and application to some nonlinear integro-differential equations corresponding to fractional-order time derivative, Adv. Differential Equ. 7 (2002), 217–236.

    MathSciNet  MATH  Google Scholar 

  15. T. Kato, Blow-up of solutions of some nonlinear hyperbolic equations, Commun. Pure Appl. Math. 33 (1980), 501–505.

    Article  MathSciNet  MATH  Google Scholar 

  16. A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations, vol 204. Elsevier Science B.V., Amsterdam, 2006.

    Book  MATH  Google Scholar 

  17. I. Kim, K.H. Kim, S. Lim, An \(L_q(L_p)\)-theory for the time fractional evolution equations with variable coefficients, Adv. Math. 306 (2017), 123–176.

    Article  MathSciNet  MATH  Google Scholar 

  18. M. Li, C. Chen, F.B. Li, On fractional powers of generators of fractional resolvent families, J. Funct. Anal. 259 (2010), 2702–2726.

    Article  MathSciNet  MATH  Google Scholar 

  19. K. Li, J. Peng, J. Xia, Cauchy problems for fractional differential equations with Riemann-Liouville fractional derivatives, J. Funct. Anal. 263 (2012), 476–510.

    Article  MathSciNet  MATH  Google Scholar 

  20. Y.N. Li, H.R. Sun, Z.S. Feng, Fractional abstract Cauchy problem with order \(\alpha \in (1,2)\), Dyna. PDE 13(2) (2016), 155–177.

    MathSciNet  MATH  Google Scholar 

  21. R. Metzler, J. Klafter, The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, J. Phys. A 37 (2004), 161–208.

    Article  MathSciNet  MATH  Google Scholar 

  22. R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep. 339 (2000), 1–77.

    Article  MathSciNet  MATH  Google Scholar 

  23. M.M. Meerschaert, E. Nane and P. Vellaisamy, Fractional Cauchy problems on bounded domains, Ann. Probab. 37 (2009), 979–1007.

    Article  MathSciNet  MATH  Google Scholar 

  24. C.X. Miao, H. Yang, The self-similar solution to some nonlinear integrodifferential equations corresonding to fractional order time derivate, Acta. Math. Sin. 21 (2005), 1337–1350.

    Article  MATH  Google Scholar 

  25. E. Mitidieri, S.I. Pohozaev, A priori estimates and blow-up of solutions to nonlinear partial differential equations and inequalities, Proc. Steklov Inst. Math. 234 (2001), 1–383.

    MATH  Google Scholar 

  26. A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations, Springer, New York, 1983.

    Book  MATH  Google Scholar 

  27. I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999.

    MATH  Google Scholar 

  28. R. Ponce, V. Poblete, Maximal \(L_p\)-regularity for fractional differential equations on the line, Math. Nachr. 290 (2017), 2009–2023.

    Article  MathSciNet  MATH  Google Scholar 

  29. J.Prüss, Evolutionary Integral Equations and Applications, Monographs in Mathematics 87, Birkhäuser, Basel, 1993.

    Book  Google Scholar 

  30. P. Quittner, P. Souplet, Superlinear Parabolic Problems: Blow-up, Global Existence and Steady States, Birkhäuser, Basel, 2007.

    MATH  Google Scholar 

  31. K. Sakamoto, M. Yamamoto, Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems, J. Math. Anal. Appl. 382 (2011), 426–447.

    Article  MathSciNet  MATH  Google Scholar 

  32. R.N. Wang, D.H. Chen, T.J. Xiao, Abstract fractional Cauchy problems with almost sectorial operators, J. Differ. Equ. 252 (2012), 202–235.

    Article  MathSciNet  MATH  Google Scholar 

  33. J.Y. Wang, Y. Zhou, Analysis of nonlinear fractional control systems in Banach spaces, Nonlinear Anal. 74 (2011), 5929–5942.

    Article  MathSciNet  MATH  Google Scholar 

  34. B.T. Yordanov, Q.S. Zhang, Finite time blow-up for critical wave equations in high dimensions, J. Funct. Anal. 231 (2006), 361–374.

    Article  MathSciNet  MATH  Google Scholar 

  35. R. Zacher, Convergence to equilibrium for second order differential equations with weak damping of memory type, Adv. Differential Equ. 14 (2009), 749–770.

    MathSciNet  MATH  Google Scholar 

  36. R. Zacher, Maximal regularity of type \(L_p\) for abstract parabolic Volterra equations, J. Evol. Equ. 5 (2005), 79–103.

    Article  MathSciNet  MATH  Google Scholar 

  37. R. Zacher, A De Giorgi-Nash type theorem for time fractional diffusion equations, Math. Ann. 356 (2013), 99–146.

    Article  MathSciNet  MATH  Google Scholar 

  38. Q.G. Zhang, H.R. Sun, The blow-up and global existence of solutions of Cauchy problems for a time fractional diffusion equation, Topol. Methods Nonlinear Anal. 46(1) (2015), 69–92.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the anonymous referee for valuable comments and suggestions. This work is partially supported by National Natural Science Foundation of China (Grant Nos. 11526108, 11601216).

Author information

Authors and Affiliations

  1. Department of Mathematics, Luoyang Normal University, Luoyang, 471022, Henan, People’s Republic of China

    Quanguo Zhang

  2. College of Mathematics & Statistics, Nanjing University of Information Science & Technology, Nanjing, Jiangsu , 210044, People’s Republic of China

    Yaning Li

Authors
  1. Quanguo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yaning Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Quanguo Zhang or Yaning Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Q., Li, Y. Global well-posedness and blow-up solutions of the Cauchy problem for a time-fractional superdiffusion equation. J. Evol. Equ. 19, 271–303 (2019). https://doi.org/10.1007/s00028-018-0475-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00028-018-0475-x

Keywords

Search

Navigation