1 Introduction

Despite their commercial importance and many years of study, Pb(Zr1−x Ti x )O3 (PZT) ceramics are still poorly understood. Although there is general consensus on the broad regions of stability of the different phases (Figure 1) and that the important region for piezo response properties is close to the so-called morphotropic phase boundary (MPB),[1] there is still much debate about the mechanisms that give rise to their exceptional properties and about the detailed structure and symmetries that are present on the local scale.

Fig. 1
figure 1

Schematic phase diagram of PZT

Full size image

The majority of work that has been carried out to characterize the atomic scale structure of the different phases has used X-ray or neutron powder diffraction together with Rietveld analysis.[2–5] For the high-temperature (paraelectric) phase, Kuroiwa et al.[5] found that PZT has a simple cubic perovskite structure, but with a disordered Pb site such that the Pb is displaced away from the center of its surrounding cage of 12 O2− ions into any one of a number of symmetry-related positions. For Zr-rich compositions, the Pb ions appeared to be distributed over eight possible sites, each shifted along one of the \( \langle 111\rangle_{c} \) directions, whereas for Ti-rich compositions, the Pb ions appeared to be distributed over the 12 possible sites shifted in the \( \langle 110\rangle_{c} \) directions. Here, the subscript c refers to the cubic perovskite cell.

In contrast, the structural models obtained for the low-temperature rhombohedral phases, which are ferroelectric, have all assumed a single, basically ordered Pb position with a static shift from the center of its coordination shell of oxygens. Basically the same structure has been found for a wide range of compositions from x = ~0.13 to 0.40,[2,4] though some variation of the magnitude of the cation shifts was reported. Figure 2 shows the structure drawn using the coordinates of Dmowski et al.[4] This clearly shows the displacement of the Pb (δ Pb) and the Zr/Ti (δ Zr) sites along the rhombohedral [001] h axis direction, relative to the oxygen octahedra. Here, the subscript h refers to the hexagonal setting of the rhombohedral cell. This is the \( \langle 111\rangle \) direction of the rhombohedral setting.

Fig. 2
figure 2

Drawing of the structure of the R3c phase of PZT made using the coordinates of Dmowski et al.[4] Note the static cation shifts δ Pb and δ Zr, which are referred to in the text

Full size image

Given this strong body of evidence for the nature of the rhombohedral phase, it was therefore surprising when it was discovered that highly structured diffuse scattering was present in electron diffraction patterns.[3] Although the diffuse scattering patterns that have been observed were most distinct for compositions around x = 0.3, they have been observed across the entire rhombohedral composition range, even extending into the MPB region and the tetragonal phase.[3] Because these existing structural models are ordered (apart from the occupational disorder of the perovskite B-site cations), they are unable to account for the presence of this highly structured diffuse scattering.

A typical diffraction pattern is shown in Figure 3. This shows two prominent sets of diffuse streaks. Dashed lines have been drawn to highlight one of the sets of streaks and have been labeled with the corresponding order number of each streak. The streaking is clearly transverse polarized, since the zeroth-order streak is missing. In fact, the diffuse streaks have been shown[6] to correspond to the intersection with the reciprocal lattice section of diffuse planes of scattering in three dimensions, each set being normal to one of the cubic \( \langle 111\rangle_{c} \) directions.

Fig. 3
figure 3

A [531] c zone-axis electron diffraction pattern of a x = 0.3 sample of PZT. Two prominent sets of diffuse streaks are visible. One of these sets is emphasized by the labeled dashed lines. Note that the zeroth-order diffuse streak is absent

Full size image

In a recent article,[6] we have shown that the scattering can be explained by a simple model in which Pb atoms are displaced away from the average site position in any one of the eight possible cubic \( \langle 111\rangle_{c} \) directions, and these displacements are correlated along chains (single rows of Pb sites) running along \( \langle 111\rangle_{c} \) also. A small representative region of a single layer of Pb sites from this model is shown in Figure 4, where examples of the aligned rows of arrows representing the Pb shifts can be seen.

Fig. 4
figure 4

A small region of a single layer normal to [1\( \overline{1} \)0] of the fully cubic model structure for PZT, showing the correlated chains of Pb shifts[6]

Full size image

Although the crystals are clearly rhombohedral, with the rhombohedral axis c h being slightly larger than a c  × 2√3 and a h  ≈ a c  × √2, the diffuse scattering appears to retain overall cubic symmetry. Consequently, to demonstrate the origins of the scattering, a model that retained average cubic symmetry was constructed. At any site in this model crystal, a Pb atom was displaced by a fixed amount along any one of the eight possible \( \langle 111\rangle_{c} \) directions with equal probability. This was assumed in order to ensure that diffuse planes occurred normal to each of the different \( \langle 111\rangle_{c} \) directions, and so basically the same diffraction pattern is obtained whether it is recorded, for example, down the [531] c zone axis, as in Figure 3, or down [5\( \overline{3} \)1] c , [135] c , etc.

The problem with this model is that, while it appears to give a good description of the observed diffuse scattering, it is quite incompatible with the published structural models for the rhombohedral phase, derived from powder diffraction, that have cation shifts only along a single [111] c direction. In fact, this model might be considered to be appropriate for the high-temperature cubic phase of PZT, where a multisite Pb position has been proposed. Although no diffuse diffraction patterns for the high-temperature phase of PZT are available, very similar diffraction patterns showing the same kind of transverse polarized streaks are observed in the related material PZLT, which is cubic at ambient temperatures.[7]

The aim of the present article is to show how this conflict can be resolved by assuming that the low-temperature phases contain a residual component of the disorder that is ubiquitous in the high-temperature phase. This means that the structural modeling of these phases needs to be reappraised, which in turn will have significant ramifications for the understanding of the origins of the material’s properties.

2 Proposed Model

As outlined previously, it has been assumed in all structural studies of the low-temperatures phases that the disorder present in the paraelectric cubic phase has been lost when going through the phase transition so that the Pb shifts are all pointing in the same direction, [111] c or [001] h (Figure 2). This is, however, not to be expected for an order-disorder phase transition, and there are numerous theoretical models of phase transitions that show that significant disorder is still present well below the transition temperature. Figure 5 shows a schematic drawing of the variation of magnetization with temperature for a Heisenberg model (e.g., Stanley[8]). Similar results occur for models that use discrete (binary) variables, e.g., Ising models. In fact, it is also pertinent to mention here that while quantities such as the magnetization (or site occupancy) show an abrupt change at the phase transition, pair correlations can vary smoothly through the transition.[9,10] This means that diffuse scattering below the transition point may be similar in form (have a similar correlation structure) to that above it. An example showing this kind of behavior may be found in Reference 11.

Fig. 5
figure 5

Schematic graph of the magnetization vs temperature for a Heisenberg model[8]

Full size image

In order to test whether this is a viable explanation for the PZT case, we set up the following model: Suppose that the occupancy of each Pb site is defined by an eight-state variable, σ ijk . The different values of σ ijk specify along which of the cubic \( \langle 111\rangle_{c} \) directions the particular Pb ion is displaced. The indices i, j, and k define the position of a particular unit cell in the crystal along the cubic x, y, and z directions, respectively. We suppose that a fraction, p, of these correspond to displacements along [111] c and a fraction (1 – p)/7 to displacements along each of the other seven \( \langle 111\rangle_{c} \) directions. Thus, p = 0.125 corresponds to the cubic situation where all eight \( \langle 111\rangle_{c} \) directions are equivalent, while p = 1.0 corresponds to the perfectly ordered rhombohedral case with Pb displacements along [111] c only. A quantity M = (p − 0.125)/0.875 would then correspond to an occupancy variable comparable to the magnetization in Figure 5.

A second comparable set of variables,ρ ijk , is used to represent the displacements of the (Zr,Ti) B-site cations. In our earlier study, the value of each of these variables was calculated approximately by prescription from the values of the eight surrounding σ ijk variables. In the present case, both sets of variables were included in the interaction model.

Irrespective of any correlations that might exist between the σ ijk and ρ ijk variables, the preceding description defines an average structure, which will give rise to Bragg peak intensities. The first aim in assessing this disordered model as a viable representation of the real PZT structure is to see whether an ordered structural model can equally well fit the Bragg peak intensities (powder diffraction data) produced by it. Section III is concerned with these aspects of the study.

The second aim in assessing this disordered rhombohedral model is to investigate whether it is still able to produce diffuse scattering patterns in agreement with the observed patterns and still display essentially cubic symmetry for values of p ≫ 0.125. In order to do this, a model is developed in which the neighboring Pb and (Zr,Ti) ions interact and so produce correlations between the σ ijk and ρ ijk variables. Section IV is concerned with these aspects of the study.

For the purposes of this article, we restrict a detailed discussion to a model in which p = 0.51. This corresponds to 51 pct of the Pbs being shifted along [111] and 7 pct along each of the other seven \( \langle 111\rangle_{c} \) directions. The basic off-center shifts of the Pb ions were taken to be (±δ, ±δ, ±δ) with δ = 0.07 in fractional coordinates referred to the simple cubic cell. This value corresponds to a shift of approximately 0.5 Å along the body diagonals and is of a magnitude that bond-valence calculations suggest the Pb ion needs to move to satisfy its valence of 2.0.[12–14] It should be noted that the mean shift that results is given by (q, q, q), where

$$ q = [(p - (1 - p)/7) \times \delta ] $$
(1)

For p = 0.51, q = 0.031; and for p = 0.70, q = 0.046.

3 Simulated Powder Diffraction

The disordered structure described in Section II was constructed in the program “CrystalMaker” using the space group P1 with a = b = c = 4.10 Å and α = β = γ = 89.5 deg and atom positions as defined in Table I. A drawing of the structure obtained is shown in Figure 6 viewed down [111]. The companion program “CrystalDiffract” was then used to generate a simulated X-ray powder diffraction pattern of this structure. A calculated profile with data points at intervals of 0.02 deg of 2θ for Cu K α over the range 0 to 96.9 deg, with the peak width parameter set to 0.15 deg and a Lorentzian line profile, was written to a file.

Table I Atomic Fractional Coordinates and Site Occupancies in the Simulated Model Structure; This Was Constructed in the Space Group P1 with a = b = c = 4.10 Å and α = β = γ = 89.5 Deg
Full size table
Fig. 6
figure 6

Drawing of the model structure viewed down [111] c showing the cluster of cation sites distributed around the center of the coordination polyhedron

Full size image

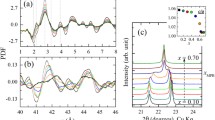
These data were then used as input to the Rietveld refinement program Rietica.[15] This was used to fit a perfectly ordered model to the data assuming that the structure had the rhombohedral space group R3. The fit obtained is shown in Figure 7.

Fig. 7
figure 7

Fit to the simulated powder diffraction profile obtained from the model disordered crystal using a simple ordered rhombohedral model for the crystal

Full size image

The fit is excellent and this simple experiment has clearly demonstrated that a model containing no disorder can perfectly well fit powder diffraction data obtained from fairly drastically disordered crystal, even when the Rietveld modeling makes no allowance for this disorder. This suggests that it is possible that Rietveld studies of PZT are not sensitive to the type of disorder we are positing, and that the disorder apparent from our electron diffraction experiments is indeed present, but usually undetected, in most if not all PZT samples.

This result has important implications for any studies in which Rietveld refinement is used to model a structure that has the potential to contain disorder. If disorder is present and not suspected, then refinement using a purely ordered model will clearly lead to a flawed description, even if the refinement gives a good fit. While an average structure model will not model the local ordering, it must allow the local ordering to exist. In this case, this means that the Pb sites must be modeled as split or disordered sites; otherwise, there are no different displacements that can be locally ordered by the Monte Carlo (MC) model. Just as averaging across the disorder model must recover the average structure, the average structure must be one that allows the disorder to exist. This is an important piece of information for a Rietveld refinement. We have shown that if heed is paid to the local bond-valence requirements of constituent ions and judicial use made of constraints and restraints, a realistic model that includes the disorder and describes the average satisfactorily can be found.

3.1 Monte Carlo Simulation of Disorder

A MC computer model was set up using the σ ijk and ρ ijk variables described earlier, which represent cation displacements along the eight different [111] c directions away from their idealized cubic site positions. For use in the equations that follow, these variables are considered to have unit length.

First, Pb and (Zr,Ti) shifts were set up to be completely random; that is, each σ ijk and each ρ ijk were arbitrarily assigned one of the eight values given in Table II but not with equal probability. Fifty-one percent of the values were chosen to have a [111] c displacement and 7 pct to have displacements in the other seven \( \langle 111\rangle_{c} \) directions. In the course of the MC simulation, variables on pairs of sites were simply interchanged. As a result, this initial distribution of the proportions displaced in the different directions remained unchanged throughout. Consequently, the average structure and the Bragg peak intensities were unaffected by the ordering process described subsequently.

Table II Eight Different Values Taken by ψ N  = (x, y, z), Which Defines The Possible Values of the Displacement Variables σ ijk and ρ ijk *
Full size table

Correlation was introduced into the arrays of variables using an MC energy of the form

$$ E_{\text{crystal}} = \sum\limits_{\text{All Pb sites,}\,{\it n}} {} \sum\limits_{\text{n.n. (Zr,Ti)}\,{\it m}=1,8} {} F\left( {\sigma_{n} ,\rho_{m} } \right) = \sum\limits_{\text{All Zr/Ti sites,}\,{\it n}} {} \sum\limits_{\text{n.n. Pb}\,{\it m}=1,8} {} F\left( {\rho_{n} ,\sigma_{m} } \right) $$
(2)

Here, the summations are over all nearest-neighbor pairs of sites, i.e., eight (Zr,Ti) sites around each Pb or vice versa. The function F is given by

$$ F_{N} \left( {\sigma_{n} ,\rho_{m} } \right) = \left\{ {\begin{array}{*{20}c} { - J_{N} } \hfill & {} \hfill & {{\text{if }}\sigma_{\text{n}} {\cdot} \rho_{m} = 1} \hfill \\ {} \hfill & {} \hfill & {{\text{and }}\sigma_{\text{n}} {\cdot} \Uppsi_{\text{N}} = \pm 1} \hfill \\ { 0} \hfill & {} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(3)

Here, Ψ N defines the direction of the vector joining the particular pair of σ n and ρ m variables. The term J N is an interaction energy along that vector. Initially, only a single value for J N was used, but subsequently, the values for the different \( \langle 111\rangle_{c} \) directions were allowed to be different (as discussed subsequently). Equations [2] and [3] simply state that there is an energy preference for neighboring variables to be aligned parallel to each other and parallel to the vector joining them. All other conformations give zero contribution to the energy.

The normal MC algorithm[16] was used as follows. Two sites in the crystal, i 1, j 1, k 1 and i 2, j 2, k 2, were chosen at random, and the variables associated with them, σ i1,j1,k1 or ρ i1,j1,k1 and σ i2,j2,k2 or ρ i2,j2,k2, were interchanged. For each interchange, either two σ variables were used or two ρ. The contribution to the energy of all terms dependent on the interchanged variables was computed using Eq. [3] before and after the change was made. The energy difference, ΔE = E new − E old, was used to decide whether the new configuration should be kept or the system returned to the original configuration. A pseudorandom number, η, chosen uniformly in the range 0 → 1, was compared with the transition probability, P = exp(−ΔE/kB T), where T is the temperature and kB the Boltzmann’s constant. If η < P, the new configuration was accepted, while if η > P, it was rejected and the system returned to the original state. An MC cycle is defined as that number of such individual steps needed to visit each site once on average. In the simulations presented in this article, we assumed T = 1/kB and 500 cycles of iteration were used.

After each cycle of iteration counting, statistics were obtained from the σ ijk and ρ ijk arrays to obtain values for the correlations that had been induced between neighboring displacements.

Let Ψ N define the vector from a given Pb site to the Nth neighboring (Zr,Ti) site. Suppose P N is the joint probability that both the Pb site and the (Zr,Ti) site have a displacement parallel to Ψ N . Similarly, suppose the fraction of Pb sites that have a displacement parallel to Ψ N is f N . Since we have assumed the distribution of the two sets of variables σ ijk and ρ ijk to be the same, the fraction of (Zr,Ti) sites that have a displacement parallel to Ψ N is also f N . Then, a correlation coefficient between these displacements can be defined:

$$ {{C_{N} = \left( {P_{N} - f_{N}^{2} } \right)} \mathord{\left/ {\vphantom {{C_{N} = \left( {P_{N} - f_{N}^{2} } \right)} {\left( {f_{N} \left( {1 - f_{N} } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f_{N} \left( {1 - f_{N} } \right)} \right)}} $$
(4)

Such correlation coefficients were calculated for neighbors in each of the 8 \( \langle 111\rangle_{c} \) directions, N. These values were compared to a particular target correlation value that was desired, and the discrepancy at any stage was used to adjust the value of the corresponding J N for the next cycle. In this way, the iteration progressed toward a final distribution in which the same nearest neighbor correlation had been induced for each of the eight types of \( \langle 111\rangle_{c} \) shifts. After some experimentation, it was found that the fact that over 50 pct of the shifts were directed along [111] c meant that there was a strong likelihood that neighbors in this direction would take on the desired structure even if there was no correlation as such. Hence, the correlation in this direction was not well defined for such a small statistical sample and better results were obtained when J N was set to zero for N corresponding to this polar direction. In the examples presented here, therefore, shifts in the polar direction were not directly correlated, but correlations were induced in the other 7 \( \langle 111\rangle_{c} \) directions, as given by Eq. [3]. For the p = 0.51 example, the resulting value of J N /kBT was 50, while for the p = 0.70 example, a much higher value of J N /kBT = 3200 was required.

4 Results of MC

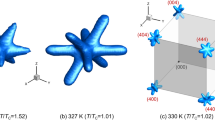
Figure 8(a) shows a representative region of a single layer of the structure normal to [1\(\bar{1}\)0] c for the model with p = 0.51, showing the distribution of cation displacements. In this figure, ±[111] c and ±[11\(\bar{1}\)] c displacements lie in the plane of the paper and the dominance of the [111] c direction is obvious. Nevertheless, the fact that there are correlations in all four \( \langle 111\rangle_{c} \) directions means that rows of aligned displacement vectors can be seen in the other three directions, including \([\bar{1}\bar{1}\bar{1}]_{c}\). Figure 8(b) shows a comparable representative region of a single layer of the structure normal to [1\(\bar{1}\)0] c for a comparable distribution, but in which the polar direction has been switched from [111] c to [1\(\bar{1}\)1] c . Now the dominant direction is out of plane. Figures 8(c) and (d) show, for comparison, comparable plots for a model with p = 0.70.

Fig. 8
figure 8

The distribution of displacement vectors of the simulated structure in a representative small region of a single layer normal to [1\( \overline{1} \)0]. (a) and (b) p = 0.51; and (c) and (d) p = 0.70. A correlation value C N  = 0.2 was used for both. [111] was the polar vector in (a) and (c), while [1\( \overline{1} \)1] was the polar vector for (b) and (d)

Full size image

Figure 9 shows diffraction patterns calculated for models in which p was either 0.51 or 0.70. The section shown is for the [531] c zone axis and so corresponds to the observed pattern shown in Figure 3. This particular section was chosen because it is one of the sections for which we have data showing most clearly the diffuse streaking. It should be noted that the models produce diffuse planes of scattering normal to each of the four \( \langle 111\rangle_{c} \) directions so that a given section has four sets of diffuse planes that intersect it. In practice, observed patterns appear to show only two of these at any time. This was explained in our previous article[6] as being due to the angle with which the diffuse planes intersect the particular section. For the [531] c zone axis, ±[111] c and ±[11\(\bar{1}\)] c are inclined steeply to the plane of the section and so are quite visible, while ±[1\( \bar{1}\)1] c and ±[\( \bar{1}\)11] c are only shallowly inclined and are not nearly so visible. Diffraction patterns were calculated using the program DIFFUSE.[17] This calculates the diffuse scattering only, since the average structure is subtracted during the calculation. The Bragg peaks have been superposed on the patterns shown in Figure 9 to aid comparison with the observed patterns.

Fig. 9
figure 9

Diffraction pattern for the [531] c zone axis obtained from the simulated structure (cf. Fig. 2). (a) and (b) p = 0.51; and (c) and (d) p = 0.70. A correlation value C N  = 0.2 was used for both. [111] c was the polar vector in (a) and (c), while \([1{\bar{1}} 1]_{c} \) was the polar vector for (b) and (d)

Full size image

Despite the fact that the models are strongly rhombohedral with over 50 and 70 pct of the cations displaced in a single \( \langle 111\rangle_{c} \) direction, the form of the diffuse scattering patterns that have been achieved is very similar to that of patterns obtained for a purely cubic model that has equal occurrence of all eight different \( \langle 111\rangle_{c} \) shifts. Coupled with the powder refinement results described in Section III, this provides a convincing explanation of what is happening in the real material.

Of particular significance in the discussion of the diffuse scattering in PZT is the “transverse polarized” nature of the scattering discussed in Section II. This requires that the direction of correlation of the displaced cations is parallel to the displacement direction. This results in the extinction of the zeroth-order diffuse plane, as indicated in Figure 2. For the models presented here, it should be noted that, as p increases from 0.125 to the values 0.51 or 0.70 used in these examples, the average cation position shifts from the original position at the center of the coordination polyhedra along the [111] vector. This average position is what is observed in the powder refinements. In the present case, the basic off-center shift of the Pb ions was taken to be (δ, δ, δ) with δ = 0.07 in fractional coordinates referred to the simple cubic cell. This fixed shift was used throughout. The average position of the Pb site corresponding to the two simulations was (q, q, q) with q = 0.031 for p = 0.51 and q = 0.046 for p = 0.70.

Since the diffuse scattering arises from the difference between the particular atomic positions and the average position, the actual shifts giving rise to the diffuse intensity must be measured relative to this average position. This means that as q departs significantly from zero, the direction of the displacements, measured from the new average position, is no longer parallel to the correlation direction. This is shown schematically in Figure 10. Figures 10(a) and (b) show the eight possible displaced Pb sites (smaller gray balls) around the central ideal position (large black ball) as viewed down the [531] c axis. For Figure 10(a), [111] c is the rhombohedral polar direction so the average Pb position (light colored (blue online) ball) is shifted in that direction. Since [111] c has a large component out of the plane of the diagram, the perceived shift (arrow) is quite small. As a result, the perceived shift vectors (dashed lines) relative to this average position are no longer parallel to the \( \langle 111\rangle_{c} \) correlation vectors (solid lines), but deviate by a relatively small amount. Figure 10(b) shows a comparable drawing for the case when [1\( \bar{1}\)1] c is the rhombohedral polar direction. Now the perceived shift vectors (dashed lines) relative to the average position are much further from the ideal \( \langle 111\rangle_{c} \) directions. In both cases, the condition for transverse polarization is violated, but the discrepancy is much greater for (b).

Fig. 10
figure 10

Schematic drawing of the various Pb displacement vectors as viewed down [531] c . The large central ball is the ideal Pb position at the center of the coordination polyhedron. The small light (blue online) ball is the average position of the Pb for the models in which a large fraction of the displacements are along (a) [111] c or (b) [1\(\bar{1}\)1] c

Full size image

The effect of this can be seen in the diffraction patterns of Figure 9. For Figures 9(a) and (c), the [531] zone axis corresponds to a situation corresponding to Figure 10(a), where the average Pb site position is shifted with its largest component out of the plane of the paper. Consequently, viewed from this direction, the correlated displacements are still fairly close to parallel to the correlation direction, and these two patterns still have the appearance of transverse polarization.

In contrast, for Figures 9(b) and (d), the average position is shifted along [1\(\bar{1}\)1] c and corresponds to the situation shown in Figure 10(b). The shift of the average position now has a large lateral component. Consequently, the displacements giving rise to the diffuse bands in these patterns are no longer in the same direction as the correlation and the scattering is no longer completely transverse polarized. The zeroth-order band stretching between the two “A’s” is quite strong, although for the other main set of bands, the zeroth-order position stretching between “B’s” is still virtually absent. The effect is much more marked for the p = 0.70 case, as would be expected.

The significance of this is that such effects should be observable in the real material. Generally speaking, observed patterns have invariably appeared to be strongly “transverse polarised;” however, no systematic survey has been carried out to see if exceptions occur. In fact, on close scrutiny of the pattern shown in Figure 3, though the numbered set of diffuse lines does appear to show the extinction of the zeroth-order line, there is some slight indication of intensity in the zeroth order of the other, unmarked set of prominent lines.

Another consideration that may affect the ability to observe these effects is that such electron diffraction patterns are invariably obtained by illumination of a relatively large area of specimen, and the possibility that different twinned orientations are simultaneously present cannot be ruled out.

5 Conclusions

In this article, we have shown that in order to explain the diffuse scattering that is observed in the room-temperature phases of PZT, it must be accepted that these still contain a significant amount of the disorder that is present in the high-temperature (paraelectric) phase. At present this is at odds with the currently accepted structural models that have been used to describe the low temperature rhombohedral and tetragonal phases. For these, a perfectly ordered model is assumed in which the Pb ions are all displaced along the same direction.

A model has been developed that allows a large fraction, p (>50 pct), of the cations to be displaced away from the center of their coordination polyhedra along a single \( \langle 111\rangle_{c} \) direction but still having a significant fraction displaced in each of the other seven \( \langle 111\rangle_{c} \) directions. It has been shown that such a disordered model will give a powder diffraction pattern that can be fitted quite satisfactorily with a model that assumes no disorder. At the same time, the model gives diffuse scattering patterns very similar to those observed with electron diffraction.

Bond valence or apparent valence calculations show invariably in these Pb perovskite systems that the Pb ions are so underbonded that they must shift away from the center of their coordination polyhedron by about 0.5 Å. The shift that is actually observed in powder Rietveld refinements is rather less.[2,4] The current model suggests that what is being measured is the average shift, which is dependent on p and is given by Eq. [1].

The model developed here to show the origins of the diffuse planes of scattering used a basic MC energy (Eq. [2] and [3]) that induced correlations along independent chains of Pb and (Zr/Ti) ions. No consideration was given to the possibility of lateral correlations nor to any local relaxation processes. As a result of this, the diffuse planes of scattering in the calculated patterns are of virtually uniform intensity. It is clear that the observed patterns do show some variation of intensity along the length of the streaks, and this presents an opportunity for further study. It might be noted here that the patterns that have been observed for PZLT[7] show a variation somewhat different from those for PZT, although the basic pattern of diffuse sheets is the same.

For the purposes of the simulations presented here, the geometric rhombohedral distortion of the parent cubic cell was ignored. Clearly, if the occupancy parameter p is 0.125, making the average cation sites conform to the cubic symmetry, there will be no reason for the cubic cell to distort. As soon as p becomes >0.125 and the displacements in one of the \( \langle 111\rangle_{c} \) directions becomes dominant (even if only slightly), then such a rhombohedral distortion would follow naturally. The magnitude of the distortion would be expected to depend not only on the magnitude of p, but also on the fine details of the chemical bonding and local interactions.