Alterations in electroosmotic slip velocity: combined effect of viscoelasticity and surface potential undulation

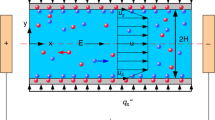
Abstract

In computational models of microchannel flows, the Helmholtz–Smoluchowski slip velocity boundary condition is often used because it approximates the motion of the electric double layer without resolving the charge density profiles close to the walls while drastically reducing the computational effort needed for the flow model to be solved. Despite working well for straight channel flow of Newtonian fluids, the approximation does not work well for flow involving complex fluids and spatially varying surface potential distribution. To treat these effects using the slip velocity boundary condition, it is necessary to understand how the surface potential and fluid properties affect the slip velocity. The present analysis shows the existence of a modified electroosmotic slip velocity for viscoelastic fluids, which is strongly dependent upon Deborah number and viscosity ratio, and this modification differs significantly from the slip velocity of Newtonian fluids. An augmentation of fluid elasticity results in an asymmetric distribution of slip velocity. Nonintuitively, the modulation wavelength of the imposed surface potential contributes to changing the slip velocity magnitude and adding periodicity to the solution. The proposed electroosmotic slip velocity for viscoelastic fluid can be used in computational models of microchannel flows to approximate the motion of the electric double layer without resolving the charge density profiles close to the walls.

Appendix 1: Stress components of various order of asymptotic series expansion

In order to assess the flow velocity, we need to first obtain the stress components from the Oldroyd-B constitutive equations after expanding the terms asymptotically. Here, for the inner layer, we have presented the normal and shear stress components for various order of corrections.

1.1 Constitutive relation for the $O(\beta ^2)$ stress components

The constitutive relation for the $O(\beta ^2)$ stress components in the inner layer becomes

$$\begin{aligned} \begin{aligned} \boxed {{\widetilde{\tau }}_{xx,02}}=0; \quad \boxed {\widetilde{\tau }_{xy,02}}=\frac{\partial {\widetilde{u}}_{02}}{\partial \widetilde{y}}; \quad \boxed {{\widetilde{\tau }}_{yy,02}}=2\frac{\partial \widetilde{v}_{02}}{\partial {\widetilde{y}}} \end{aligned} \end{aligned}$$

(30)

here, ${\widetilde{\tau }}_{xx,02}$ becomes zero and $\widetilde{\tau }_{xy,02}$ and ${\widetilde{\tau }}_{yy,02}$ have dependency on $O(\beta ^2)$ velocity components only.

1.2 Constitutive relation for the $O(\mathrm{{De}}\beta ^2)$ stress components

We move towards obtaining the constitutive relation for the $O(\mathrm{{De}}\beta ^2)$ stress components in the inner layer, which reads

$$\begin{aligned} \boxed {{\widetilde{\tau }}_{xx,{12}}}&=-4\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{x}}}\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}} +2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,{02}}+2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,{02}}\\&\quad +2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,01}+2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,01} \\ &\quad +2\frac{\partial {\widetilde{u}}_{02}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,0}+2\frac{\partial {\widetilde{u}}_{02}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,0}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_{02}-\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_{02}\\ &\quad -\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}-\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,{02}}}{\partial {\widetilde{x}}}{\widetilde{u}}_0-\frac{\partial {\widetilde{\tau }}_{xx,{02}}}{\partial {\widetilde{y}}}{\widetilde{v}}_0\\ \boxed {{\widetilde{\tau }}_{xy,{12}}}&=\frac{\partial {\widetilde{u}}_{12}}{\partial {\widetilde{y}}}-2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{v}}_{01}}{\partial {\widetilde{y}}} +\frac{\partial ^2 {\widetilde{u}}_0}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{01}+\frac{\partial ^2 {\widetilde{u}}_0}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{01}\\&\quad +\frac{\partial ^2 {\widetilde{u}}_{01}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{0}+\frac{\partial ^2 {\widetilde{u}}_{01}}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{0} +\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,{02}}+\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,01}\\&\quad +\frac{\partial {\widetilde{u}}_{02}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,0}+\frac{\partial {\widetilde{v}}_0}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,{02}} +\frac{\partial {\widetilde{v}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,01}+\frac{\partial {\widetilde{v}}_{02}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,0}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_{02}-\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_{02} -\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}-\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}\\ &\quad-\frac{\partial {\widetilde{\tau }}_{xy,{02}}}{\partial {\widetilde{x}}}{\widetilde{u}}_0 -\frac{\partial {\widetilde{\tau }}_{xy,{02}}}{\partial {\widetilde{y}}}{\widetilde{v}}_0\\ \boxed {{\widetilde{\tau }}_{yy,{12}}}&=2\frac{\partial \widetilde{v}_{12}}{\partial {\widetilde{y}}} +2\frac{\partial ^2 \widetilde{v}_0}{\partial {\widetilde{y}} \partial {\widetilde{x}}}\widetilde{u}_{01}+2\frac{\partial ^2 {\widetilde{u}}_0}{\partial \widetilde{y}^2}{\widetilde{v}}_{01}\\&\quad +2\frac{\partial ^2 {\widetilde{v}}_{01}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{0}+\frac{\partial ^2 {\widetilde{v}}_{01}}{\partial {\widetilde{y}}^2}\widetilde{v}_0-8\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_{01}}{\partial \widetilde{y}}\\ &\quad -2\frac{\partial {\widetilde{u}}_{01}}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{x}}-2\frac{\partial {\widetilde{u}}_0}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_{01}}{\partial \widetilde{x}}\\&\quad +2\frac{\partial {\widetilde{v}}_0}{\partial {\widetilde{x}}}\widetilde{\tau }_{xy,{02}}+2\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,{02}}+2\frac{\partial \widetilde{v}_{01}}{\partial {\widetilde{x}}}\widetilde{\tau }_{xy,01}\\&\quad +2\frac{\partial {\widetilde{v}}_{01}}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,01} +2\frac{\partial \widetilde{v}_{02}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xy,0}\\&\quad +2\frac{\partial {\widetilde{v}}_{02}}{\partial {\widetilde{y}}}\widetilde{\tau }_{yy,0}-\frac{\partial {\widetilde{\tau }}_{yy,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_{02} -\frac{\partial \widetilde{\tau }_{yy,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_{02}\\&\quad-\frac{\partial {\widetilde{\tau }}_{yy,01}}{\partial {\widetilde{x}}}\widetilde{u}_{01} -\frac{\partial {\widetilde{\tau }}_{yy,01}}{\partial \widetilde{y}}{\widetilde{v}}_{01}\\&\quad -\frac{\partial \widetilde{\tau }_{yy,{02}}}{\partial {\widetilde{x}}}{\widetilde{u}}_0-\frac{\partial {\widetilde{\tau }}_{yy,{02}}}{\partial {\widetilde{y}}}{\widetilde{v}}_0 \end{aligned}$$

(31)

here, the normal stress component ${\widetilde{\tau }}_{xx,{12}}$ is dependent on the leading order, $O(\beta )$, and $O(\beta ^2)$ stress and velocity components. The other two stress components i.e. ${\widetilde{\tau }}_{xy,{12}}$ and ${\widetilde{\tau }}_{yy,{12}}$ depend on the $O(\mathrm{{De}}\beta ^2)$ velocity component along with the leading order, $O(\beta )$, and $O(\beta ^2)$ stress and velocity components.

1.3 Constitutive relation for the $O(\mathrm{{De}}^2)$ stress components

We obtain the constitutive relation for the $O(\mathrm{{De}}^2)$ stress components in the inner layer, which are

$$\begin{aligned} \boxed {{\widetilde{\tau }}_{xx,20}}&=-{\widetilde{u}}_0\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{x}}}-{\widetilde{u}}_{10}\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{x}}}\\&\quad -{\widetilde{v}}_0\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{y}}}-{\widetilde{v}}_{10}\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{y}}}\\&\quad +2{\widetilde{\tau }}_{xx,0}\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{x}}}+2{\widetilde{\tau }}_{xx,10}\frac{\partial {\widetilde{u}}_{0}}{\partial {\widetilde{x}}}\\&\quad +2{\widetilde{\tau }}_{xy,0}\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}+2{\widetilde{\tau }}_{xy,10}\frac{\partial {\widetilde{u}}_{0}}{\partial {\widetilde{y}}}\\ \boxed {{\widetilde{\tau }}_{xy,20}}&=\frac{\partial {\widetilde{u}}_{20}}{\partial {\widetilde{y}}}-u_0\frac{\partial {\widetilde{\tau }}_{xy,10}}{\partial {\widetilde{x}}}-{\widetilde{u}}_{10}\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{x}}}\\&\quad -{\widetilde{v}}_0\frac{\partial {\widetilde{\tau }}_{xy,10}}{\partial {\widetilde{y}}}-{\widetilde{v}}_{10}\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{y}}}\\&\quad +{\widetilde{\tau }}_{xx,0}\frac{\partial {\widetilde{v}}_{10}}{\partial {\widetilde{x}}}+{\widetilde{\tau }}_{xx,10}\frac{\partial {\widetilde{v}}_{0}}{\partial {\widetilde{x}}}+{\widetilde{\tau }}_{yy,0}\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}\\ &\quad +{\widetilde{\tau }}_{yy,10}\frac{\partial {\widetilde{u}}_{0}}{\partial {\widetilde{y}}}\\ \boxed {{\widetilde{\tau }}_{yy,20}}&=2\frac{\partial \widetilde{v}_{20}}{\partial {\widetilde{y}}}-{\widetilde{u}}_0\frac{\partial {\widetilde{\tau }}_{yy,10}}{\partial {\widetilde{x}}}\\&\quad -\widetilde{u}_{10}\frac{\partial {\widetilde{\tau }}_{yy,0}}{\partial \widetilde{x}}-{\widetilde{v}}_0\frac{\partial {\widetilde{\tau }}_{yy,10}}{\partial {\widetilde{y}}}-{\widetilde{v}}_{10}\frac{\partial \widetilde{\tau }_{yy,0}}{\partial {\widetilde{y}}}\\&\quad +2\widetilde{\tau }_{xy,0}\frac{\partial {\widetilde{v}}_{10}}{\partial \widetilde{x}}+2{\widetilde{\tau }}_{xy,10}\frac{\partial {\widetilde{v}}_{0}}{\partial {\widetilde{x}}}+2{\widetilde{\tau }}_{yy,0}\frac{\partial \widetilde{v}_{10}}{\partial {\widetilde{y}}}\\ & \quad +2\widetilde{\tau }_{yy,10}\frac{\partial {\widetilde{v}}_{0}}{\partial {\widetilde{y}}} \end{aligned}$$

(32)

here, the normal stress component ${\widetilde{\tau }}_{xx,20}$ is dependent on the leading order and $O(\mathrm{{De}})$ stress and velocity components. The other two stress components i.e. $\widetilde{\tau }_{xy,20}$ and ${\widetilde{\tau }}_{yy,20}$ depend on the $O(\mathrm{{De}}^2)$ velocity component along with the leading order and $O(\mathrm{{De}})$ stress and velocity components.

1.4 Constitutive relation for the $O(\mathrm{{De}}^2\beta )$ stress components

Then we proceed to obtain the constitutive relation for the $O(\mathrm{{De}}^2\beta )$ stress components in the inner layer, which are of the form   

$$\begin{aligned} \boxed {{\widetilde{\tau }}_{xx,{21}}}&=-4\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}+2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,1}\\&\quad +2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,1}+2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,10}+2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,10}\\&\quad +2\frac{\partial {\widetilde{u}}_1}{\partial x}{\widetilde{\tau }}_{xx,0} +2\frac{\partial {\widetilde{u}}_{1}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,0}+2\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,01}\\&\quad +2\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,01}-\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_1-\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_1\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_{10}-\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{y}}}{\widetilde{v}}_{10}-\frac{\partial {\widetilde{\tau }}_{xx,1}}{\partial {\widetilde{x}}}{\widetilde{u}}_0\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,1}}{\partial {\widetilde{y}}}{\widetilde{v}}_{0}-\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}-\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}\\ \boxed {{\widetilde{\tau }}_{xy,{21}}}&=\frac{\partial {\widetilde{u}}_{21}}{\partial {\widetilde{y}}}-2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{v}}_{10}}{\partial {\widetilde{y}}}-2\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{v}}_{0}}{\partial {\widetilde{y}}}\\&\quad +\frac{\partial ^2 {\widetilde{u}}_0}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{10}+\frac{\partial ^2 {\widetilde{u}}_0}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{10}+\frac{\partial ^2 {\widetilde{u}}_{10}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{0}\\&\quad +\frac{\partial ^2 {\widetilde{u}}_{10}}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{0}+\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,1}+\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,10}\\&\quad +\frac{\partial {\widetilde{u}}_1}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,0}+\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,01}+\frac{\partial {\widetilde{v}}_0}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,1}\\&\quad +\frac{\partial {\widetilde{v}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,10}+\frac{\partial {\widetilde{v}}_1}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,0}\\&\quad +\frac{\partial {\widetilde{v}}_{10}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,01}-\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_1-\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_1\\&\quad -\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_{10}-\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{y}}}{\widetilde{v}}_{10}-\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_0\\&\quad -\frac{\partial {\widetilde{\tau }}_{xy,1}}{\partial {\widetilde{y}}}{\widetilde{v}}_0-\frac{\partial {\widetilde{\tau }}_{xy,10}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}-\frac{\partial {\widetilde{\tau }}_{xy,10}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}\\ \boxed {{\widetilde{\tau }}_{yy,{21}}}&=2\frac{\partial \widetilde{v}_{21}}{\partial {\widetilde{y}}}+2\frac{\partial ^2 \widetilde{v}_{10}}{\partial {\widetilde{y}}^2}{\widetilde{v}}_0\\&\quad +2\frac{\partial ^2 {\widetilde{v}}_{0}}{\partial {\widetilde{y}}^2}\widetilde{v}_{10}-8\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_{10}}{\partial \widetilde{y}}\\&\quad -2\frac{\partial {\widetilde{u}}_{10}}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{x}}-2\frac{\partial {\widetilde{u}}_0}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_{10}}{\partial \widetilde{x}}\\&\quad -2\frac{\partial {\widetilde{u}}_0}{\partial \widetilde{y}}\frac{\partial {\widetilde{v}}_{01}}{\partial \widetilde{x}}-\frac{\partial {\widetilde{\tau }}_{yy,1}}{\partial \widetilde{x}}{\widetilde{u}}_0-\frac{\partial {\widetilde{\tau }}_{yy,1}}{\partial {\widetilde{y}}}{\widetilde{v}}_0\\&\quad -\frac{\partial \widetilde{\tau }_{yy,10}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}-\frac{\partial {\widetilde{\tau }}_{yy,10}}{\partial {\widetilde{y}}}\widetilde{v}_{01}-\frac{\partial {\widetilde{\tau }}_{yy,0}}{\partial \widetilde{y}}{\widetilde{v}}_1\\&\quad -\frac{\partial \widetilde{\tau }_{yy,{01}}}{\partial {\widetilde{x}}}\widetilde{u}_{10}-\frac{\partial {\widetilde{\tau }}_{yy,01}}{\partial \widetilde{y}}{\widetilde{v}}_{10}+2\frac{\partial {\widetilde{v}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,10}\\&\quad +2\frac{\partial \widetilde{v}_{1}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,0}+2\frac{\partial {\widetilde{v}}_{10}}{\partial {\widetilde{x}}}\widetilde{\tau }_{xy,01}+2\frac{\partial {\widetilde{v}}_{10}}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,01}\\&\quad -\frac{\partial \widetilde{\tau }_{yy,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_1+2\frac{\partial ^2 {\widetilde{v}}_{0}}{\partial {\widetilde{y}} \partial \widetilde{x}}{\widetilde{u}}_{10}+2\frac{\partial ^2 {\widetilde{v}}_{10}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_{0}\\&\quad +2\frac{\partial {\widetilde{v}}_0}{\partial {\widetilde{x}}}\widetilde{\tau }_{xy,1}+2\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,1}+2\frac{\partial {\widetilde{v}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xy,10} \end{aligned}$$

(33)

here, the normal stress component ${\widetilde{\tau }}_{xx,{21}}$ is dependent on the leading order, $O(\mathrm{{De}})$, $O(\beta )$ and $O(\mathrm{{De}}\beta )$ stress and velocity components. The other two stress components i.e. ${\widetilde{\tau }}_{xy,{21}}$ and ${\widetilde{\tau }}_{yy,{21}}$ depend on the $O(\mathrm{{De}}^2\beta )$ velocity component along with the leading order, $O(\mathrm{{De}})$, $O(\beta )$ and $O(\mathrm{{De}}\beta )$ stress and velocity components.

1.5 Constitutive relation for the $O(\mathrm{{De}}^2\beta ^2)$ stress components

Then we proceed to obtain the constitutive relation for the $O(\mathrm{{De}}^2\beta ^2)$ stress components in the inner layer, which reads   

$$\begin{aligned} \boxed {{\widetilde{\tau }}_{xx,{22}}}&=-4\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{u}}_1}{\partial {\widetilde{y}}}-4\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}\\&\quad +2\frac{\partial {\widetilde{u}}_{02}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,10}+2\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,{12}}+2\frac{\partial {\widetilde{u}}_{02}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,10}\\&\quad +2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,1}-\frac{\partial {\widetilde{\tau }}_{xx,{12}}}{\partial {\widetilde{y}}}{\widetilde{v}}_0-\frac{\partial {\widetilde{\tau }}_{xx,{02}}}{\partial {\widetilde{x}}}{\widetilde{u}}_{10}\\&\quad +2\frac{\partial {\widetilde{u}}_{12}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,0}+2\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,{02}}+2\frac{\partial {\widetilde{u}}_{0}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,{12}}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,{12}}}{\partial {\widetilde{x}}}{\widetilde{u}}_0+2\frac{\partial {\widetilde{u}}_{12}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,0}+2\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,{02}}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{y}}}{\widetilde{v}}_1-\frac{\partial {\widetilde{\tau }}_{xx,01}}{\partial {\widetilde{x}}}{\widetilde{u}}_1-\frac{\partial {\widetilde{\tau }}_{xx,1}}{\partial {\widetilde{x}}}{\widetilde{u}}_{01}\\&\quad +2\frac{\partial {\widetilde{u}}_1}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,01}+2\frac{\partial {\widetilde{u}}_{01}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{xy,1}-\frac{\partial {\widetilde{\tau }}_{xx,{02}}}{\partial {\widetilde{y}}}{\widetilde{v}}_{10}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{x}}}{\widetilde{u}}_{{02}}-\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_{12}+2\frac{\partial {\widetilde{u}}_1}{\partial x}{\widetilde{\tau }}_{xx,01}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xx,1}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}-\frac{\partial {\widetilde{\tau }}_{xx,10}}{\partial {\widetilde{y}}}{\widetilde{v}}_{{02}}-\frac{\partial {\widetilde{\tau }}_{xx,0}}{\partial {\widetilde{x}}}{\widetilde{u}}_{12}\\ \boxed {{\widetilde{\tau }}_{xy,{22}}}&=\frac{\partial \widetilde{u}_{22}}{\partial {\widetilde{y}}}+\frac{\partial ^2 \widetilde{u}_{01}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}\widetilde{u}_{10}\\&\quad +\frac{\partial ^2 {\widetilde{u}}_{1}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}{\widetilde{u}}_0+\frac{\partial ^2 \widetilde{u}_{10}}{\partial {\widetilde{y}} \partial {\widetilde{x}}}\widetilde{u}_{01}+\frac{\partial {\widetilde{u}}_1}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,01}-\frac{\partial \widetilde{\tau }_{xy,1}}{\partial {\widetilde{x}}}\widetilde{u}_{01}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xy,{02}}}{\partial {\widetilde{x}}}{\widetilde{u}}_{10}+\frac{\partial \widetilde{v}_1}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,01}-\frac{\partial {\widetilde{\tau }}_{xy,{12}}}{\partial {\widetilde{y}}}\widetilde{v}_{0}\\&\quad +\frac{\partial {\widetilde{u}}_{01}}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,1}+\frac{\partial {\widetilde{u}}_0}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,{12}}-\frac{\partial \widetilde{\tau }_{xy,0}}{\partial {\widetilde{x}}}\widetilde{u}_{{12}}\\&\quad +\frac{\partial {\widetilde{u}}_{02}}{\partial \widetilde{y}}{\widetilde{\tau }}_{yy,10}+\frac{\partial {\widetilde{u}}_{12}}{\partial {\widetilde{y}}}{\widetilde{\tau }}_{yy,0}-\frac{\partial \widetilde{\tau }_{xy,10}}{\partial {\widetilde{x}}}{\widetilde{u}}_{02}\\&\quad +\frac{\partial {\widetilde{u}}_{10}}{\partial {\widetilde{y}}}\widetilde{\tau }_{yy,{02}}-\frac{\partial {\widetilde{\tau }}_{xy,1}}{\partial {\widetilde{y}}}{\widetilde{v}}_{01}+\frac{\partial \widetilde{v}_{02}}{\partial {\widetilde{x}}}\widetilde{\tau }_{xx,10}\\&\quad +\frac{\partial {\widetilde{v}}_{01}}{\partial \widetilde{x}}{\widetilde{\tau }}_{xx,1}+\frac{\partial {\widetilde{v}}_{10}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,{02}}\\&\quad +\frac{\partial \widetilde{v}_{12}}{\partial {\widetilde{x}}}{\widetilde{\tau }}_{xx,0}-\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial {\widetilde{x}}}\widetilde{u}_{1}-\frac{\partial {\widetilde{\tau }}_{xy,10}}{\partial \widetilde{y}}{\widetilde{v}}_{02}\\&\quad -\frac{\partial \widetilde{\tau }_{xy,{12}}}{\partial {\widetilde{x}}}\widetilde{u}_{0}\\&\quad +\frac{\partial ^2 {\widetilde{u}}_1}{\partial \widetilde{y}^2}{\widetilde{v}}_{0}+\frac{\partial ^2 {\widetilde{u}}_{10}}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{01}+\frac{\partial ^2 \widetilde{u}_0}{\partial {\widetilde{y}}^2}{\widetilde{v}}_{1}+\frac{\partial ^2 {\widetilde{u}}_{01}}{\partial {\widetilde{y}}^2}\widetilde{v}_{10}\\&\quad -\frac{\partial {\widetilde{\tau }}_{xy,01}}{\partial \widetilde{y}}{\widetilde{v}}_1-\frac{\partial {\widetilde{\tau }}_{xy,0}}{\partial {\widetilde{y}}}{\widetilde{v}}_{12}\\&\quad -\frac{\partial \widetilde{\tau }_{xy,{02}}}{\partial {\widetilde{y}}}\widetilde{v}_{10}+\frac{\partial {\widetilde{v}}_0}{\partial \widetilde{x}}{\widetilde{\tau }}_{xx,{12}}-2\frac{\partial \widetilde{u}_{01}}{\partial {\widetilde{y}}}\frac{\partial \widetilde{v}_{01}}{\partial {\widetilde{y}}} \end{aligned}$$

(34)

here,the stress components i.e. ${\widetilde{\tau }}_{xy,{22}}$ and ${\widetilde{\tau }}_{yy,{22}}$ are depend on the $O(\mathrm{{De}}\beta ^2)$ velocity component along with the leading order, $O(\mathrm{{De}})$, $O(\beta )$, $O(\mathrm{{De}}\beta )$, $O(\beta ^2)$, and $O(\mathrm{{De}}\beta ^2)$ stress and velocity components.