Melnikov’s method applied to accidental phase modulation phenomenon

Abstract

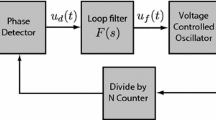
The performance of clock recovery phase-locked loop (PLL) can be severely degraded by unwanted spurious phase modulation, due to noise and nonlinearities associated with the transmission medium. Consequently, choosing appropriate circuit parameters to avoid or at least reduce these undesirable effects plays a crucial role in achieving a successful PLL circuit. This paper demonstrates that Melnikov’s method, originally proposed to identify chaos in dynamic systems, can be successfully used to establish the appropriate circuit parameters by determining the regions that ensure the correct operation under conditions of noise and nonlinearities, represented by periodic perturbations. This study considers the use of one of the most commonly adopted configurations for clock recovery, the second-order PLL with lag-lead filter, and provides a valuable tool for circuit dimensioning and design of clock distribution networks.

Appendix: Heteroclinic chaos and Melnikov method

Considering that chaos refers to apparently stochastic behaviors in nonlinear dynamical systems described by differential equations, experimental work was developed showing the existence of chaotic attractors in pendulum and Joseph junction time evolution, when excited by signals following: $A + B\sin \omega \cdot t$, with A, B and $\omega$ constants [28,29,30].

For this type of system, theoretical development was conducted in [21, 22, 31] modeling the experiments in an accurate way by treating the whole system as a perturbation from a Hamiltonian, constructing the Melnikov measure [19] that can be used to predict chaotic behaviors as described in this section.

For systems presenting chaotic behaviors, there are regions in the phase space such that, starting the temporal evolution in two closed points, as time passes, the distance between their destinations increases exponentially. If a system presents saddle equilibrium points, i.e., a singularities related to four distinct trajectories, two tending to the singularity as $t \rightarrow +\infty$, called stable manifolds; and two as $t \rightarrow -\infty$, called unstable manifolds. If there are transversal interceptions between the stable and unstable manifolds associated to a saddle equilibrium point indicate this kind of dynamical behavior [19], i.e., the presence of heteroclinic points in these interceptions is responsible for the onset of chaos [31].

There are slightly different techniques to detect heteroclinic chaos, firstly described in [23, 31, 32]. In [23], a version of the Melnikov’s method was developed for second-order Hamiltonian systems with a heteroclinic orbit, with an additional periodic perturbation. As it is shown in the next section, the accidental phase modulation in PLLs can be modeled following the same type of equation, justifying this brief description of the method to be used.

Considering second-order systems described by:

$$\begin{aligned} \left\{ \begin{array}{ccc} \dot{u} = \epsilon p_{0}(u,v) + \epsilon p_{1} (u,v,\theta ,\epsilon ); \\ \dot{v} = \epsilon q_{0}(u,v) + \epsilon q_{1} (u,v,\theta ,\epsilon ) \, ; \\ {{\dot{\theta }}} = \dfrac{2 \cdot \pi }{T}, \,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \end{array} \right. \nonumber \\ \end{aligned}$$

(24)

with $(u,v) \in \mathfrak {R}^{2}$; $p_{0}, p_{1}, q_{0}$ and $q_{1}$ continuous functions; $\theta \in \mathfrak {R}$; $T \in \mathfrak {R}_{+}$; and $\epsilon \in \mathfrak {R}$, $\epsilon > 0$, and small.

Concerning systems described by (24), they can be viewed as described by $\epsilon$-perturbations of the autonomous equations:

$$\begin{aligned} \left\{ \begin{array}{ccc} \dot{u} = \epsilon p_{0}(u,v); \\ \dot{v} = \epsilon q_{0}(u,v); \\ {{\dot{\theta }}} = \dfrac{2 \cdot \pi }{T}. \,\,\,\,\,\,\,\,\, \end{array} \right. \nonumber \\ \end{aligned}$$

(25)

About equations (24) and (25), the following hypothesis are supposed to be true:

• H-1: they present two hyperbolic saddle points: $x_{0}{'} = (u_{0}{'},v_{0}{'})$ and $x_{0}{''} = (u_{0}{''},v_{0}{''})$, connected by a trajectory $\varGamma _{0}$;

• H-2: if $x_{0} \in \varGamma _{0} \Rightarrow$ $\lim _{t\rightarrow +\infty } x(t) = x_{0}'$, and $\lim _{t\rightarrow -\infty } x(t) = x_{0}'';$

• H-3: functions $p_{0}, p_{1}, q_{0}$ and $q_{1}$ are $2 \cdot \pi$ periodic in $\theta$, and of ${\mathcal {O}} (\epsilon ).$

Lemma 1

Under the hypotheses H-1, H-2 and H-3, the following statement can be proved:

• Equations (24) and (25) present orbits $\gamma '$ and $\gamma ''$, respectively, with stable and unstable manifolds $E^{s}(\gamma '), E^{u}(\gamma '), E^{s}(\gamma '')$ and $E^{u}(\gamma '')$ with transversal section ${\varSigma _{t_o} = (u,v,\theta ) \in \mathfrak {R}^{2} \times S^{1} \mid _{\theta =t_0}}$.

The proof of this Lemma can be found on page 69 of [22].

Considering the facts described, Melnikov proved [31] that solutions of (24) can be written as:

$$\begin{aligned} x(t) = x_{0}(t) + \sum _{k} \epsilon ^{k} \cdot x_{k} (t). \end{aligned}$$

(26)

Consequently, the solutions appearing in the stable and unstable manifolds, $E^{s}(\gamma ')$ and $E^{u}(\gamma '')$, belonging to a compact neighborhood of the equilibrium points, can be expressed by:

$$\begin{aligned} \left\{ \begin{array}{cc} x_{\epsilon }^{s}(t) = x_{0}(t) + \epsilon \cdot x_{1}^{s}(t) + {\mathcal {O}} (\epsilon ^{2}); \, \\ x_{\epsilon }^{u}(t) = x_{0}(t) + \epsilon \cdot x_{1}^{u}(t) + {\mathcal {O}} (\epsilon ^{2}), \end{array} \right. \end{aligned}$$

(27)

with $x_0$ being the non-perturbed orbit of $\varGamma _0$.

It must be observed that $x_{0}(t)$ is a heteroclinic non-perturbed orbit; $x_{\epsilon }^{s}(t)$ and $x_{\epsilon }^{u}(t)$ are the stable and unstable perturbed orbits, respectively. The Melnikov method evaluates the distance between $x_{\epsilon }^{s}(t,t_o)$ and $x_{\epsilon }^{u}(t,t_0)$, because if they intercept each other in one point, there is an infinite number of interceptions between these orbits, originating the Smale horseshoe [23] in the Poincaré map dynamics [19], with a set of unstable orbits with different periods, that seem to be non-periodic recurrent orbits.

This fact occurs if the separation measure between $x_{\epsilon }^{s}(t,t_o)$ and $x_{\epsilon }^{u}(t,t_0)$, here called $d_{\epsilon }(t_0) = \varDelta (t_0)$, presents transversal zeros, i.e., there is a $t^{'}_{0}$ such that: $\varDelta (t^{'}_0=0)$ and ${\dfrac{d\varDelta }{dt} \mid _{t^{'}_0}}=0$.

Considering the notation and conditions described in this section, as shown in [23, 32], the Melnikov measure is given by:

$$\begin{aligned} \varDelta (t_0) = [f_{0}(x_{0}(0))] \wedge [x^{s}(t_0) - x^{u}(t_0)]. \end{aligned}$$

(28)

In equation (28):

• for $f_{0} = (p_0,q_0)$ and x(u, v); $f_{0} \wedge x = p_0 \cdot v - q_0 \cdot u$;

• $x_{0}(t) = (p_{0}(t),q_{0}(t))$ is the solution of the non-perturbed system, i.e., of Eq. (25);

• $x^{s}(t)$ and $x^{u}(t)$ are the solutions of the perturbed system, i.e., of Eq. (24), belonging to $E^{s}(\gamma ^{''})$ and $E^{u}(\gamma {'})$, starting in $x^{s}(t_0)$ and $x^{u}(t_0)$ in section ${\varSigma _{t_o} = (u,v,\theta ) \in \mathfrak {R}^{2} \times S^{1} \mid _{\theta =t_0}}$.

The measure defined by Eq. (28) is useful to look for chaotic attractors for second-order systems. However, in practical cases, it is difficult to obtain the analytic expressions for $x^{s}(t_0)$ and $x^{u}(t_0)$ and, consequently, it is usual to expresses the Melnikov measure as the approximation:

$$\begin{aligned} \varDelta (t_0) = \varDelta _{1}(t_0) + {\mathcal {O}} (\epsilon ^{2}), \end{aligned}$$

(29)

with:

$$\begin{aligned} \varDelta _{1}(t,t_0) =&f_{0}(x_{0}(t-t_{0})) \wedge [x_{1}^{s}(t-t_0) - x_{1}^{u}(t-t_0)]\nonumber \\&= \varDelta _{1}^{s}(t-t_0) - \varDelta _{1}^{u}(t-t_0). \end{aligned}$$

(30)

Calculating the first term of the power approximation for the solution, expressed by the Jacobian [19, 22], it can be written that:

$$\begin{aligned}&\varDelta (t_0) = - \int _{-\infty }^{+\infty } {[f_{0}(x_{0}(t-t_0)) \wedge f_{1}(x_{0}(t-t_0;t))]} \cdot \nonumber \\&{\exp \left[ -\int _{0}^{t-t_0} tr J\left( f_0,x_{0}(s)\right) \mathrm{d}s\right] }\mathrm{d}t + {\mathcal {O}} (\epsilon ^{2}), \end{aligned}$$

(31)

with J representing the Jacobian matrix.

If the unperturbed system is Hamiltonian [19], the exponential term vanishes, resulting that:

$$\begin{aligned}&\varDelta (t_0) = - \int _{-\infty }^{+\infty } (f_{0} \wedge f_{1})\mathrm{d}t \nonumber \\&\quad = - \int _{-\infty }^{+\infty } (p_{0}q_{1} - p_{1}q_{0})\mathrm{d}t + {\mathcal {O}} (\epsilon ^{2}). \end{aligned}$$

(32)

This methodology was applied to the PLL problem identifying its dynamic equation with (24) and constructing the Melnikov measure for this particular problem. Then, searching for transversal zeros in the measure, the forbidden parameter regions were found, concerning accidental phase modulation as a perturbation.