Skip to main content
SpringerLink
Log in

Effects of symmetry-breaking on the dynamics of the Shinriki’s oscillator

  • Regular Article
  • Published:
The European Physical Journal Special Topics Aims and scope Submit manuscript

Abstract

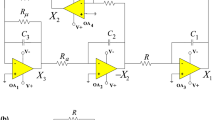
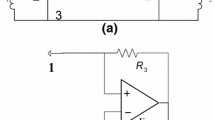
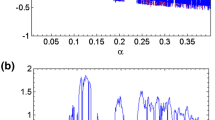
We investigate the dynamics of the well-known Shinriki’s oscillator both in its symmetric and asymmetric modes of operation. Instead of using the classical approximate cubic model of the Shinriki’s oscillator, we propose a close form model by exploiting the Shockley exponential diode equation. The proposed model takes into account the intrinsic characteristics of semiconductor diodes forming the nonlinear part (i.e., the positive conductance). We address the realistic issue of symmetry-breaking by considering different numbers of diodes within the two branches of the positive conductance. The dynamics of the system is investigated by exploiting conventional nonlinear analysis tools such as bifurcation diagrams, phase-space trajectories plots, basins of attractions, and graphs of Lyapunov exponent as well. In the symmetric mode of operation, the system experiences coexisting symmetric attractors, period-doubling route to chaos, and merging crisis. The symmetry breaking analysis yields two asymmetric coexisting bifurcation branches (i.e., asymmetric bi-stability) each of which exhibits its own sequence of bifurcations to chaos when monitoring the main control parameter. In this special mode, the merging process never occurs; instead, one of the bifurcation branches vanishes when decreasing the control parameter beyond a critical value following a crisis event. The theoretical results are validated by carrying out laboratory experimental studies of the physical circuit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data Availability Statement

My manuscript has no associated data or the data will not be deposited.

References

  1. L. Pivka, C.W. Wu, A. Huang, Chua’s oscillator: a compendium of chaotic phenomena. J. Franklin Inst. 331B(6), 705–741 (1994)

    Article  MathSciNet  Google Scholar 

  2. H.B. Fotsin, P. Woafo, Adaptive synchronization of a modified and uncertain chaotic Van der Pol-Duffing oscillator based on parameter identification. Chaos Solitons Fractals 24, 1363–1371 (2005)

    Article  MathSciNet  ADS  Google Scholar 

  3. M. Shinriki, M. Yamato, S. Mori, Multimode oscillations in a modified van der Pol oscillator containing a positive nonlinear conductance. Proc. IEEE 69, 394–395 (1981)

    Article  Google Scholar 

  4. E. Freire, L.G. Franquelo, J. Aracil, Periodicity and chaos in an autonomous electrical system. IEEE Trans. Circ. Syst. Vol. CAS 31(3), 237–247 (1984)

    Article  ADS  Google Scholar 

  5. J. Kengne, Z.T. Njitacke, N.A. Nguomkam, M. Fouodji Tsotsop, H.B. Fotsin, Coexistence of multiple attractors and crisis route to chaos in a novel chaotic jerk circuit. Int. J. Bifurc. Chaos 25(4), 1550052 (2015)

    Article  Google Scholar 

  6. J. Kengne, N.A. Nguomkam, Z.T. Njitacke, Antimonotonicity, chaos and multiple attractors in a novel autonomous jerk circuit. Int. J. Bifurc. Chaos 27(4), 1–20 (2017)

    MathSciNet  MATH  Google Scholar 

  7. J. Kengne, F. Kenmogne, On the modeling and nonlinear dynamics of autonomous Silva–Young type chaotic oscillators with flat power spectrum. Chaos 24, 043134 (2014)

    Article  MathSciNet  ADS  Google Scholar 

  8. C. Kahllert, The effects of symmetry breaking in Chua’s circuit and related piecewise-linear dynamical systems. Int. J. Bifurc. Chaos 3(4), 963–979 (1993)

    Article  MathSciNet  Google Scholar 

  9. S.K. Dana, S. Chakraborty, G. Ananthakrishna, Homoclinic bifurcation in Chua’s circuit. Pramana J. Phys. 64(3), 44344 (2005)

    Article  Google Scholar 

  10. H. Cao, J.M. Seoane, M.A.F. Sanjuan, Symmetry-breaking analysis for the general Helmholz–Duffing oscillator. Chaos Solitons Fractals 34, 197–212 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  11. P. Zhou, H. Cao, The effects of symmetry breaking on the parameterically excited pendulum. Chaos Solitons Fractals 38, 590–597 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  12. A. Sofroniou, S.R. Bishop, Breaking the symmetry of the parametrically excited pendulum. Chaos Solitons Fractals 28, 673–81 (2006)

    Article  MathSciNet  ADS  Google Scholar 

  13. S.R. Bishop, A. Sofroniou, P. Shi, Symmetry-breaking in the response of the parameterically excited pendulum model. Chaos Solitons Fractals 25(2), 27–264 (2005)

    Article  Google Scholar 

  14. R. Rynio, A. Okninski, Symmetry breaking and Fractal dependence on initial conditions in dynamical systems: Ordinary differential equations of thermal convection. Chaos Solitons Fractals 9(10), 1723–1732 (1998)

    Article  MathSciNet  ADS  Google Scholar 

  15. M. Henrich, T. Dahms, V. Flunkert, S.W. Teitsworth, E. Scholl, Symmetry breaking transitions in networks of nonlinear circuits elements. New J. Phys. 12, 113030 (2010)

    Article  ADS  Google Scholar 

  16. H. Cao, Z. Jing, Chaotic dynamics of Josephson equation driven by constant and ac forcings. Chaos Solitons Fractals 12, 1887–1895 (2001)

    Article  MathSciNet  ADS  Google Scholar 

  17. J. Kengne, L.K. Kengne, Scenario to chaos and multistability in a modified Coullet system: effects of broken symmetry. J. Dyn. Control Int. (2018). https://doi.org/10.1007/s40435-018-0483-2

    Article  Google Scholar 

  18. M. Hua, S. Yang, Q. Xu, M. Chen, H. Wu, B. Bao, Forward and reverse asymmetric memristor-based jerk circuits. AEU-Int. J. Electron. Commun. 20, 153294 (2020)

    Article  Google Scholar 

  19. J. Kengne, Z.T. Njitacke, T.V. Kamdoum, N.A. Nguomkam, Periodicity chaos and multiple attractors in a memristor-based Shinriki’s oscillator. Chaos 25(10), 103126 (2015)

    Article  MathSciNet  ADS  Google Scholar 

  20. W. Liu, Y. Guo, M. Lu, C. Liu, Chaos attractor compressing and expanding in Chua circuit driven by a direct current voltage. In: Proceedings of the international conference on information science and engineering, pp 446–450 (2010). https://doi.org/10.1109/ISIE.2010.105

  21. M.P. Hanias, G. Giannaris, A.R. Spyridakis, Time series analysis in chaotic diode resonator circuit. Chaos Solitons Fractals 27, 569 (2006)

    Article  ADS  Google Scholar 

  22. D.W. Sukov, M.E. Bleich, J. Gauthier, J.E.S. Socolar, Controlling chaos in a fast diode resonator using extended time-delay auto-synchronization: Experimental observations and theoretical analysis. Chaos 7(4), 560–576 (1997)

    Article  ADS  Google Scholar 

  23. H. Wu, Y. Ye, M. Chen, Q. Xu, B. Bao, Extremely slow passages in low-pass filter-based memristive oscillator. Nonlinear Dyn. 97(4), 2339–2353 (2019)

    Article  Google Scholar 

  24. B.C. Bao, P.Y. Wu, H. Bao, Q. Xu, M. Chen, Numerical and experimental confirmations of quasi-periodic behavior and chaotic bursting in third-order autonomous memristive oscillator. Chaos Solitons Fractals 106, 161–170 (2018)

    Article  MathSciNet  ADS  Google Scholar 

  25. S.H. Strogatz, Nonlinear dynamics and chaos (Addison-Wesley, Reading, 1994)

    Google Scholar 

  26. X. Jiang, X. Chen, T. Huang, H. Yan, Bifurcation and control for a predator-prey system with two delays. Express Briefs, IEEE Transactions on Circuits and Systems II (2020)

  27. A.H. Nayfeh, B. Balachandran, Applied nonlinear dynamics: analytical, computational and experimental methods (Wiley, New York, 1995)

    Book  Google Scholar 

  28. Y.A. Kuznetsov, Elements of applied bifurcation theory (Springer, New York, 1995)

    Book  Google Scholar 

  29. X. Jiang, X. Chen, M. Chi, J. Chen, On Hopf bifurcation and control for a delay systems. Appl. Math. Comput. 370, 124906 (2020)

    MathSciNet  MATH  Google Scholar 

  30. X.W. Jiang, X.S. Zhan, Z.H. Guan, X.H. Zhang, L. Yu, Neimark–Sacker bifurcation analysis on a numerical discretization of Gause-type predator-prey model with delay. J. Franklin Inst. 352(1), 1–15 (2015)

    Article  MathSciNet  Google Scholar 

  31. N.V. Kuznetsov, G.A. Leonov, M.V. Yuldashev, R.V. Yuldashev, Hidden attractors in dynamical models of phase-locked loop circuits: limitations of simulation in MATLAB and SPICE. Commun. Nonlinear Sci. Numer. Simul. 51, 39–49 (2017)

    Article  ADS  Google Scholar 

  32. G. Leonov, N. Kuznetsov, V. Vagaitsev, Hidden attractor in smooth Chua systems. Phys. D 241(18), 1482–1486 (2012)

  33. G.A. Leonov, N.V. Kuznetsov, T.N. Mokaev, Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. Eur. Phys. J. Spec. Top. 224, 1421–1458 (2015)

  34. A. Jafari, E. Mliki, A. Akgul, V.T. Pham, S.T. Kingni, X. Wang, S. Jafari, Chameleon: the most hidden chaotic flow. Nonlinear Dyn. (2017). https://doi.org/10.1007/s11071-017-3378-4

    Article  MathSciNet  Google Scholar 

  35. S. Jafari, J.C. Sportt, F. Nazarimehr, Recent new examples of hidden attractors. Eur. Phys. J. Spec. Top 224, 1469–1476 (2015)

    Article  Google Scholar 

  36. A. Wolf, J.B. Swift, H.L. Swinney, J.A. Wastano, Determining Lyapunov exponents from time series. Phys. D 16, 285–317 (1985)

    Article  MathSciNet  Google Scholar 

  37. Y.F. Wang, S.T. Qiao, J.G. Jiang, Simulation of chaos in asymmetric nonlinear Chua’s circuit. Shanghai Jiaotong Univ. (Sci) 13(4), 453–456 (2008)

    Article  Google Scholar 

  38. J.J. Healey, D.S. Broomhead, K.A. Cliffe, R. Jones, T. Mulin, The origin of chaos in a modified Van der Pol oscillator. Phys. D 4, 322–339 (1991)

    Article  MathSciNet  Google Scholar 

  39. I. Makoto, Synthesis of electronic circuits for simulating nonlinear dynamics. Int. J. Bifurc. Chaos 11, 605–653 (2001)

    Article  Google Scholar 

Download references

Acknowledgements

All authors would like to thanks the anonymous reviewers for their constructive comments, critics, and suggestions that helped to improve the content of the present paper.

Author information

Authors and Affiliations

  1. Unité de Recherche de Matière Condensée, d’Electronique et de Traitement du Signal (UR-MACETS), Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Léandre Kamdjeu Kengne & Romanic Kengne

  2. Unité de Recherche d’Automatique et Informatique Appliquée (UR-AIA), Department of Electrical Engineering, IUT-FV Bandjoun, P.O. Box 134, Bandjoun, Cameroon

    Léandre Kamdjeu Kengne & Roger Mboupda Pone

  3. Department of Electrical and Electronic Engineering, College of Technology (COT), University of Buea, P.O. Box 63, Buea, Cameroon

    Zeric Tabekoueng Njitacke

  4. Department of Electrical and Electronic Engineering, Faculty of Engineering and Technology (FET), University of Buea, P.O. Box 63, Buea, Cameroon

    Theophile Fozin Fonzin

  5. Unité de Recherche de Mécanique et de Modélisation des Systèmes Physiques (UR-2MSP), Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Hervé Thierry Kamdem Tagne

Authors
  1. Léandre Kamdjeu Kengne
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Romanic Kengne
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zeric Tabekoueng Njitacke
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Theophile Fozin Fonzin
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Roger Mboupda Pone
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Hervé Thierry Kamdem Tagne
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors have contributed equally for the preparation of the manuscript.

Corresponding author

Correspondence to Léandre Kamdjeu Kengne.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kengne, L.K., Kengne, R., Njitacke, Z.T. et al. Effects of symmetry-breaking on the dynamics of the Shinriki’s oscillator. Eur. Phys. J. Spec. Top. 230, 1813–1827 (2021). https://doi.org/10.1140/epjs/s11734-021-00130-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjs/s11734-021-00130-z

Search

Navigation