Learning DFT

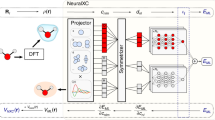
Abstract

We present an extension of reverse engineered Kohn-Sham potentials from a density matrix renormalization group calculation towards the construction of a density functional theory functional via deep learning. Instead of applying machine learning to the energy functional itself, we apply these techniques to the Kohn-Sham potentials. To this end, we develop a scheme to train a neural network to represent the mapping from local densities to Kohn-Sham potentials. Finally, we use the neural network to up-scale the simulation to larger system sizes.

Appendices

Appendix A: Neural networks for fitting functions

The main application of neural networks consists in the classification of input variables, i.e. one maps the input to a discrete set of output variable, with the standard internet example of “is it a cat or not?”. Here we provide an example for applying a neural network on fitting a function.

1.1 A.1: The network

The basic building block of a neural network (NN) consists of a neutron as depicted in Fig. 3a.

The neuron consist of an input $\{x_i\}$, weight factors $\{w_i\}$, an offset b, a so-called activation function $\sigma (z)$, see Fig. 3b, and the output z:

$$\begin{aligned} z \;=\; \sigma \left( b + \sum _\ell w_\ell x_\ell \right) \end{aligned}$$

(7)

Throughout this work we have always used an $\tanh$ activation function. One now combines many neurons, Fig. 3a, into a neural network in a layered fashion by connecting inputs of the neurons of one layer with the outputs of the neurons of the previous layer, see Fig. 4. Since from a user perspective the NN in Fig. 4 translates the input of the first layer into the output of the last layer one calls the first layer the input layer, the last one the output layer and the other layers are denoted as hidden layers. If each neuron is connected to each neuron of the previous layer one calls the network dense. The training of a NN is often referred to as machine learning, and in the presence of many hidden layer as deep learning.

Fig. 3

The building block of a NN: a a neutron, b typical weight function: a sigmoid and a $\tanh$

Fig. 4

A neural network build out of neurons shown in Fig. 3a

Fig. 5

Fits for the function f(x) Eq. (10) using a $\tanh$ activation function obtained using tensorflow/keras for a $1 \times 50 \times 50 \times 1$ network. a 25.000 samples, 10 repetitions of SGD; b 25.000 samples, 100 repetitions of SGD; c 25.000 samples, 1000 repetitions of SGD; d $2\times$ 25.000 samples, 250 repetitions ($1\times$ SGD & $1\times$ADAM)

In summary, the NN in Fig. 4 calculates an output z from the input $\{x_j\}$, where one has to specify the parameter in Eq. (7) for each neuron n in layer $\ell$,

$$\begin{aligned} z_{\ell ,n} \;=\; \sigma \left( b_{\ell ,n} + \sum _j w_{\ell ,n,j} x_j \right) \,. \end{aligned}$$

(8)

Of course, this can be extended to create multiple output variables $z_k$ in the output layer.

In order to apply a NN for fitting functions f(x) we use a NN with a single input x and a single output z. The free parameter $\{b_{\ell ,n}, w_{\ell ,n,j}\}$ are the set of fitting parameter. We would like to note that this approach is in contrast to the desired approach in physics, where on tries to fit a phenomenon with a suitable function using as few fitting parameter as possible. Instead, here we take the opposite approach by using a simple fitting function unrelated to the problem and fit the desired function with a large number of parameter and a few steps of recursion.

1.2 A.2: Training the neural network: minimize cost function

The idea to determine the fit parameter for fitting a function $f(\mathbf{x})$ consists in minimizing a cost function, typically

$$\begin{aligned} C(\mathbf{x}) \;=\; \frac{1}{N} \sum _{i=1}^{N} \left| \left| f(\mathbf{x}_i) - z_{\{b_{\ell ,n}, w_{\ell ,n,j}\}}(\mathbf{x}_i) \right| \right| _2 \end{aligned}$$

(9)

where N denotes the number of training samples. Eq. (9) could in principle be minimized by a standard steepest descent gradient search. However, due the vast amount of fit parameter this is not feasible in non-trivial examples, as the number of parameter, and therefore the dimensions of the associated matrices get too large. The breakthrough for neural networks was provided by the invention of the back propagating algorithm [14] combined with a stochastic evaluation of the gradients [36,37,38] combined the massive computational power of graphic cards, and for pattern recognition the use of convolutional layers [15], see below. In the example provided in this section we used tensorflow [17] software package combined with the keras [18] front end.

Fig. 6

Fits for the function f(x) Eq. (10) using a $\tanh$ activation function obtained using tensorflow/keras for a $1 \times 250 \times 50 \times 50 \times 1$ network, 250 repetitions, (SGD & ADAM)

1.3 A.3: An example

As an example we look at the function

$$\begin{aligned} f(x) \;=\ \sin (3x) \,-\, 0.8 \cos ^2(13x) {\mathrm {e}}^{0.5 x} \,+\, 4 {\mathrm {e}}^{-\frac{x^2}{0.0005}} \,+\, 6 {\mathrm {e}}^{ -\frac{(x+0.4)^2}{0.0001}} \end{aligned}$$

(10)

which has no deeper meaning, it was just handcrafted to represent a not too trivial function combining sharp and non-sharp features.

Since f is a single valued single argument function the input and output layer consists of a single neuron only. In Fig. 5 we show the results for fitting the function f(x) in Eq. (10) with two hidden layers consisting of fifty neurons each. In result we applied a dense NN with a $1 \times 50 \times 50 \times 1$ structure. In order to train the system we generated 25.000 random values $x_j$ with the corresponding $z_j = f(x_j)$. We then trained the NN by performing a stochastic gradient descent search (SGD) with ten repetitions over the complete set of $\{x_j, z_j\}$. We then evaluate the NN on an equidistantly spaced set of $\{x_\ell \}$. As one can see in Fig. 5a the result is a rather smooth function that misses the sharp features. The way to improve the NN consists in learning harder, that is, we increased the repetitions of the SGD to 100, Fig. 5b, and 1000, Fig. 5c, which finally leads to a good representation of the functions.

A different strategy consist in using different gradient search strategies, i.e. a different optimizer to minimize the cost function Eq. (9). In Fig. 5d we show the results where we used only 500 repetitions, however we switched between a SGD and an ADAM optimizer, which performs much better, that just an SGD alone. We would like to remark that a priory it is not clear which optimizer is the best, and the optimizer performance seems to be rather problem dependent, see [12].

Finally in Fig. 6 we present results obtained from a deeper network consisting of $1 \times 250 \times 50 \times 50 \times 1$ neurons. On the right axis we show the actual error of the fit which is below $5 \times 10^{-3}$ over the complete range. In result we obtained results a rather good approximation to the function at the expense of using more than 15.000 fit parameter $\{b_{\ell ,n}, w_{\ell ,n,j}\}$.

Fig. 7

Layout for the convolutional network. The input layer is connected to two convolutional layer, which are then combined with the input layer to serve for the input of seven hidden full layers

We would like to point out that the approach of using 15.000 fit parameter may appear odd as it renders an understanding of the network impossible. However, we are using the approach to construct a DFT functional. For the ladder it is also fair to state that most users of the modern sophisticated DFT functionals have no understanding on the details of their construction.

Appendix B: A convolutional network

We also tested the setup of a convolutional network. There, in addition to full layer, one constructs a small kernel layer that gets convoluted with the with the output of another layer. For details we refer to [12].

Specifically we implemented the a NN as displayed in Fig. 7, which resulted into 100.628 fit parameter. However, despite all the effort we could not improve on the results obtained from the (smaller) dense network.