Isobaric heat capacity of classical and quantum fluids: extending experimental data sets into the critical scaling regime

Abstract

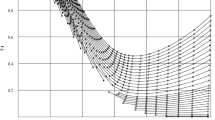
The singular isobaric heat capacity $C_{{\text{P}}} (T,P)$ of nitrogen, methane, water and hydrogen at critical pressure $P_{{\text{c}}}$ is studied over an extended temperature range, from the melting point to the high-temperature cutoff of the experimental data sets. The high- and low-temperature branches (above and below the critical temperature $T_{{\text{c}}}$) of $C_{{\text{P}}} (T,P_{{\text{c}}} )$ can accurately be modeled with broken power-law distributions in which the calculated universal scaling exponent $1 - 1/\delta$ of the isobaric heat capacity at critical pressure is implemented. (The enumerated fluids admit 3D Ising critical exponents). The parameters of these distributions are inferred by nonlinear least-squares regression from high-precision data sets. In each case, a non-perturbative analytic expression for $C_{{\text{P}}} (T,P_{{\text{c}}} )$ is obtained. The broken power laws have closed-form Index functions representing the Log–Log slope of the regressed branches of $C_{{\text{P}}} (T,P_{{\text{c}}} )$. These Index functions quantify the crossover from the experimentally more accessible high- and low-temperature regimes to the critical scaling regime. Ideal power-law scaling (without perturbative corrections and discounting impurities and gravitational rounding effects) of $C_{{\text{P}}} (T,P_{{\text{c}}} )$ occurs in a narrow interval, typically within $\left| {T/T_{{\text{c}}} - 1} \right| < 10^{ - 4}$ or even $10^{ - 5}$ depending on the fluid, and the regressed broken power-law densities provide closed-form analytic extensions of $C_{{\text{P}}} (T,P_{{\text{c}}} )$ to the melting point and up to dissociation temperatures.

Graphical Abstract

Appendices

Appendix 1

Nonlinear regression of multiply broken power laws subject to parameter constraints

The least-squares regression sketched in this appendix will be exemplified with the broken power law (2.1), which is parametrized with positive amplitudes $a_{0}$, $b_{k}$, positive exponents $\beta_{k}$, $\eta_{k}$ and real exponent $\alpha_{0}$. The amplitudes in (2.1) can be written as $b_{k} = 10^{{b_{10,k} }}$, with real exponent $b_{10,k}$ as fitting parameter, which is adapted to the decadic Log–Log representations of the heat capacity $C_{{\text{P}}} (\tau )$ in the figures.

When minimizing the least-squares functional (defined below), we use rescaled parameters $\hat{b}_{k}^{{}}$,$\hat{\beta }_{k}^{{}}$,$\hat{\eta }_{k}^{{}}$ related to $b_{k}^{{}}$,$\beta_{k}^{{}}$,$\eta_{k}^{{}}$ in (2.1) by

$$\hat{b}_{k}^{{}} = (10^{{b_{10,k} }} )^{{ - \beta_{k} /\eta_{k} }} ,\;\hat{\beta }_{k}^{{}} = \beta_{k} /\eta_{k} ,\;\hat{\eta }_{k}^{{}} = \eta_{k}^{{}} ,$$

(7.1)

and inversely,

$$b_{10,k} = {\text{Log}}(\hat{b}_{k}^{{ - 1/\hat{\beta }_{k} }} ),\;\beta_{k} = \hat{\beta }_{k}^{{}} \hat{\eta }_{k} ,\;\eta_{k}^{{}} = \hat{\eta }_{k}^{{}} .$$

(7.2)

(Log denotes the decadic logarithm, and $b_{k} = 10^{{b_{10,k} }}$.) The reparametrized $C_{{\text{P}}} (\tau )$ in (2.1) can be written as

$$C_{{\text{P}}} (\tau ) = a_{0} \tau^{{\alpha_{0} }} \frac{1}{{(1 + \hat{b}_{1}^{{}} \tau^{{\hat{\beta }_{1} }} )^{{ \, \hat{\eta }_{1} }} }}(1 + \hat{b}_{2}^{{}} \tau^{{\hat{\beta }_{2} }} )^{{ \, \hat{\eta }_{2} }} (1 + \hat{b}_{3}^{{}} \tau^{{\hat{\beta }_{3} }} )^{{ \, \hat{\eta }_{3} }} .$$

(7.3)

The exponents $\hat{\beta }_{k}^{{}}$,$\hat{\eta }_{k}^{{}}$ and amplitudes $\hat{b}_{k}^{{}}$ are positive like $\beta_{k}^{{}}$,$\eta_{k}^{{}}$,$b_{k}^{{}}$.

The asymptotic power-law scaling of $C_{{\text{P}}} (\tau )$ in (7.3) reads $C_{{\text{P}}} (\tau \to \infty )\sim A_{ + } \tau^{1 - 1/\delta }$, with exponent and amplitude related to the rescaled fitting parameters by

$$1 - 1/\delta = \alpha_{0} - \hat{\beta }_{1} \hat{\eta }_{1}^{{}} + \hat{\beta }_{2} \hat{\eta }_{2}^{{}} + \hat{\beta }_{3} \hat{\eta }_{3}^{{}} ,\;A_{ + } = a_{0} \hat{b}_{2}^{{\hat{\eta }_{2} }} \hat{b}_{3}^{{\hat{\eta }_{3} }} /\hat{b}_{1}^{{\hat{\eta }_{1} }} ,$$

(7.4)

which is the counterpart to Eqs. (2.2) in the new parametrization. By identifying $1 - 1/\delta$ with the calculated scaling exponent $0.7912$, the first identity in (7.4) becomes a constraint on the parameters, which can be used to eliminate the exponent $\alpha_{0}$ from $C_{{\text{P}}} (\tau )$ in (7.3), arriving at

$$C_{{\text{P}}} (\tau ) = A_{ + } \tau^{1 - 1/\delta } \frac{1}{{(1 + \hat{b}_{1}^{ - 1} \tau^{{ - \hat{\beta }_{1} }} )^{{ \, \hat{\eta }_{1} }} }}(1 + \hat{b}_{2}^{ - 1} \tau^{{ - \hat{\beta }_{2} }} )^{{ \, \hat{\eta }_{2} }} (1 + \hat{b}_{3}^{ - 1} \tau^{{ - \hat{\beta }_{3} }} )^{{ \, \hat{\eta }_{3} }} ,$$

(7.5)

with positive fitting parameters $A_{ + }$,$\hat{b}_{k}^{{}}$,$\hat{\beta }_{k}^{{}}$,$\hat{\eta }_{k}^{{}}$, $k = 1,2,3$. The exponent $1 - 1/\delta = 0.7912$ is predetermined input, and the amplitude $a_{0}$ in (7.3) is calculated from the regressed parameters via the second equation in (7.4).

The least-squares functional used for the regression reads

$$\chi ^{2} (A_{ + } ,(\hat{b}_{k} ,\hat{\beta }_{k} ,\hat{\eta }_{k} )_{{k = 1,2,3}} ) = \sum\limits_{{i = 1}}^{N} {\frac{{(C_{{\text{P}}} (\tau _{i} ) - C_{{{\text{P}},i}} )^{2} }}{{C_{{{\text{P}},i}}^{2} }}} ,$$

(7.6)

where $(\tau_{i} ,C_{{{\text{P}},i}} )_{i = 1,...,N}$ are the data points enumerated in Sect. 2.1 and $C_{{\text{P}}} (\tau )$ is the broken power law (7.5) depending on the fitting parameters $A_{ + }$,$(\hat{b}_{k}^{{}} ,\hat{\beta }_{k}^{{}} ,\hat{\eta }_{k}^{{}} )_{k = 1,2,3}$. Once these parameters are determined by minimization of the $\chi^{2}$ functional (7.6), we find the parameters $a_{0}$,$\alpha_{0}$ and $(b_{k}^{{}} ,\beta_{k}^{{}} ,\eta_{k}^{{}} )_{k = 1,2,3}$ of $C_{{\text{P}}} (\tau )$ in (2.1) by way of (7.2) and (7.4), cf. Table 2.

An efficient Mathematica® [44] routine to minimize a nonlinear $\chi^{2}$ functional such as (7.6) is FindMinimum[{chisquared[…],constraints},{initial values},MaxIterations → nmax]. The constraints are positivity constraints $\hat{b}_{k} > 0\quad \&\,\& \quad\hat{\beta }_{k}>0\quad \&\,\& \quad \hat{\eta }_{k}>0$, where the double ampersand denotes the logical AND. Alternatively, positivity constraints for the iteration can be avoided by replacing the parameters $(\hat{b}_{k}^{{}} ,\hat{\beta }_{k}^{{}} ,\hat{\eta }_{k}^{{}} )$ by $(\sqrt {\hat{b}_{k}^{2} } ,\sqrt {\hat{\beta }_{k}^{2} } ,\sqrt {\hat{\eta }_{k}^{2} } )$ in (7.5).

To find reasonably accurate initial values for the fitting parameters, which is essential in nonlinear multiparameter regression, one uses $C_{{\text{P}}} (\tau )$ in parametrization (2.1) rather than (7.5). The factors in (2.1) can be ordered by increasing amplitude, $b_{1} < b_{2} < ... < b_{n}$ (with $n = 3$ in (2.1)). In the range $\tau < < b_{k}$, the factors defined by the amplitudes $b_{k} , \, b_{k + 1} ,...,b_{n}$ are close to one and can be dropped. Therefore, an initial guess can be obtained by visually fitting the factors one by one, starting with the simple power law $a_{0} \tau^{{\alpha_{0} }}$ in (2.1) and increasing the $\tau$ range in each step by adding the respective data points and the respective factor. The amplitudes $b_{k}$ are the break points between the power-law segments (which are straight line segments in Log–Log plots) and the exponents $\eta_{k}$ determine the extent (curvature) of the transitional regions.