Computational model of calcium dynamics-dependent dopamine regulation and dysregulation in a dopaminergic neuron cell

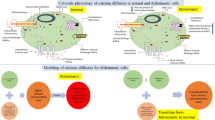
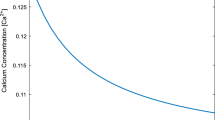
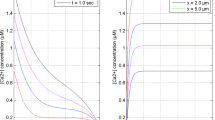
Abstract

Calcium (Ca²⁺) signaling is essential for regulating dopamine (DA) concentration levels in neurons. The alterations in the different mechanisms of [Ca²⁺] dynamics can cause the disturbances in the dopamine regulation in neuron cells. But, no attempt is reported on the spatiotemporal dependence of dopamine regulation on the [Ca²⁺] dynamics in neurons. A mathematical model is framed to explore the effects of alterations in different processes including source influx, ryanodine receptor, buffer process, serca pump, etc. on the spatiotemporal [Ca²⁺] and dopamine mechanisms in nerve cells. The Numerical findings have been acquired utilizing finite element techniques and the effects of dysregulation in diverse processes on the spatiotemporal [Ca²⁺] and dopamine mechanisms in dopaminergic neurons are analyzed. The outcomes provide the better understanding of the regulatory and dysregulatory processes, which can cause the alterations in the spatiotemporal [Ca²⁺] and dopamine dynamics leading to neuronal diseases such as Parkinson’s, attention deficit hyperactive disorder, depression, schizophrenia, etc. Thus, the present model gives novel information about the specific dysregulatory constitutive mechanisms of calcium and dopamine dynamics like source inflow, buffer, ryanodine receptor, and others, which are responsible for the elevated calcium and dopamine levels, consequently the death of dopaminergic neurons.

Appendices

Appendix 1

Model equations description

For [Ca²⁺] and dopamine mechanisms, the shape functions for each element are expressed as:

$$ u^{(e)} \, = \, q_{1}^{(e)} \, + \, q_{2}^{(e)} \, x $$

(17)

$$ v^{(e)} \, = \, r_{1}^{(e)} \, + \, r_{2}^{(e)} \, x $$

(18)

$$ {\text{u}}^{{\text{(e)}}} {\text{ = S}}^{{\text{T}}} {\text{q}}^{{\text{(e)}}} {\text{, v}}^{{\text{(e)}}} {\text{ = S}}^{{\text{T}}} {\text{r}}^{{\text{(e)}}} $$

(19)

$$ S^{T} \, = \, [\begin{array}{*{20}c} 1 & x \\ \end{array} ], \, q^{{(e)^{T} }} \, = \, [\begin{array}{*{20}c} {q_{1}^{(e)} } & {q_{2}^{(e)} } \\ \end{array} ], \, r^{{(e)^{T} }} \, = \, [\begin{array}{*{20}c} {r_{1}^{(e)} } & {r_{2}^{(e)} } \\ \end{array} ] $$

(20)

The nodal conditions in Eq. (19) yields,

$$ \overline{u}^{(e)} \, = \, S^{(e)} q^{(e)} , \, \overline{v}^{(e)} \, = \, S^{(e)} r^{(e)} , $$

(21)

where

$$ \overline{u}^{(e)} = \left[ {\begin{array}{*{20}c} {u_{i} } \\ {u_{j} } \\ \end{array} } \right],\;\overline{v}^{(e)} = \left[ {\begin{array}{*{20}c} {v_{i} } \\ {v_{j} } \\ \end{array} } \right]\;\;{\text{and}}\;\;S^{(e)} = \left[ {\begin{array}{*{20}c} 1 & {x_{i} } \\ 1 & {x_{j} } \\ \end{array} } \right] $$

(22)

By Eq. (21), we have

$$ q^{(e)} \, = \, R^{(e)} \, \overline{u}^{(e)} , \, r^{(e)} \, = \, R^{(e)} \, \overline{v}^{(e)} $$

(23)

And

$$ R^{(e)} = S^{{(e)^{ - 1} }} $$

(24)

Adding $q^{(e)}$ and $r^{(e)}$ from Eq. (23) in (19) yields,

$$ u^{(e)} \, = \, S^{T} \, R^{(e)} \, \overline{u}^{(e)} , \, v^{(e)} \, = \, S^{T} \, R^{(e)} \, \overline{v}^{(e)} $$

(25)

For Eqs. (1 and 8), the discretized form is provided as,

The integrals $I_{1}^{(e)}$ and $I_{2}^{(e)}$ can be expressed as,

$$ I_{1}^{(e)} \, = \, I_{a1}^{(e)} - \, I_{b1}^{(e)} \, + \, I_{c1}^{(e)} \, - \, I_{{{\text{d}}1}}^{(e)} \, + \, I_{e1}^{(e)} \, + \, I_{f1}^{(e)} - \, I_{g1}^{(e)} - \, I_{h1}^{(e)} $$

(26)

where

$$ I_{{{\text{a1}}}}^{{\text{(e)}}}\,\, =\,\, \int\limits_{{x_{i} }}^{{x_{j} }} {\left\{ {\left( {\frac{{\partial {\text{u}}^{{\text{(e)}}} }}{{\partial {\text{x}}}}} \right)^{2} } \right\}{\text{d}}x} $$

(27)

$$ {\text{I}}_{{{\text{b1}}}}^{{\text{(e)}}} \,\,= \,\,\frac{{\text{d}}}{{{\text{dt}}}}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {\frac{{{\text{(u}}^{{\text{(e)}}} {)}}}{{{\text{D}}_{{{\text{Ca}}}} }}} \right]{\text{ dx}}} $$

(28)

$$ {\text{I}}_{{{\text{c1}}}}^{{\text{(e)}}} \,\, = \,\,\frac{{{\text{V}}_{{{\text{IPR}}}} }}{{{\text{D}}_{{{\text{ca}}}} {\text{F}}_{{\text{c}}} }}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {{\alpha u}^{{\text{(e)}}} + {\upgamma }} \right]{\text{ dx}}} $$

(29)

$$ I_{{{\text{d}}1}}^{(e)}\,\, =\,\, \frac{{V_{{{\text{SERCA}}}} }}{{D_{{{\text{ca}}}} F_{c} }}\int\limits_{{x_{i} }}^{{x_{j} }} {\left[ {\kappa u^{(e)} + \, \eta } \right]{\text{ d}}x} $$

(30)

$$ {\text{I}}_{{{\text{e1}}}}^{{\text{(e)}}} \,\,= \,\,\frac{{{\text{V}}_{{{\text{LEAK}}}} }}{{{\text{D}}_{{{\text{ca}}}} {\text{F}}_{{\text{c}}} }}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {{\text{[Ca}}^{{2 + }} {]}_{{{\text{ER}}}} {\text{ - u}}^{{\text{(e)}}} } \right]{\text{ dx}}} $$

(31)

$$ {\text{I}}_{{{\text{f1}}}}^{{\text{(e)}}} \,\,= \,\,\frac{{{\text{V}}_{{{\text{RyR}}}} {\text{P}}_{{0}} }}{{{\text{D}}_{{{\text{ca}}}} {\text{F}}_{{\text{c}}} }}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {{\text{[Ca}}^{{2 + }} {]}_{{{\text{ER}}}} {\text{ - u}}^{{\text{(e)}}} } \right]{\text{ dx}}} $$

(32)

$$ {\text{I}}_{{{\text{g1}}}}^{{\text{(e)}}} \,\, = \,\,\frac{{{\text{K}}^{ + } }}{{{\text{D}}_{{{\text{ca}}}} }}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {{\text{u}}^{{\text{(e)}}} {\text{ - [Ca}}^{{2 + }} ]_{\infty } } \right]{\text{ dx}}} $$

(33)

$$ {\text{I}}_{{{\text{h1}}}}^{{\text{(e)}}} \,\, =\,\, {\text{f}}^{{\text{(e)}}} \frac{{\upsigma }}{{{\text{D}}_{{{\text{ca}}}} }}_{{\text{ x = 0}}} $$

(34)

_Now,

$$ {\rm I}_{2}^{\rm (e)} ={\rm I}_{\rm a2}^{\rm (e)} - {\rm I}_{\rm b2}^{\rm (e)} + {\rm I}_{\rm c2}^{\rm (e)} + {\rm I}_{\rm d2}^{\rm (e)} - {\rm I}_{\rm e2}^{\rm (e)} $$

(35)

$$ I_{{{\text{a2}}}}^{{\text{(e)}}} \,\,=\,\,\int\limits_{{x_{i} }}^{{x_{j} }} {\left\{ {\left( {\frac{{\partial v^{{\text{(e)}}} }}{\partial x}} \right)^{2} } \right\}{\text{ d}}x} $$

(36)

$$ I_{{{\text{b2}}}}^{{\text{(e)}}} \,\,= \,\,\frac{{\text{d}}}{{{\text{d}}t}}\int\limits_{{x_{i} }}^{{x_{j} }} {\left[ {\frac{{v^{(e)} }}{{{\text{D}}_{{{\text{DA}}}} }}} \right]{\text{ d}}x} $$

(37)

$$ {\text{I}}_{{{\text{c2}}}}^{{\text{(e)}}}\,\, = \,\,\frac{1}{{{\text{D}}_{{{\text{DA}}}} }}\int\limits_{{{\text{x}}_{{\text{i}}} }}^{{{\text{x}}_{{\text{j}}} }} {\left[ {[{\text{DA}}]_{{\text{P}}} {\text{f}}} \right]{\text{ dx}}} $$

(38)

$$ I_{{{\text{d2}}}}^{{\text{(e)}}} \,\,=\,\, \frac{{{\uppsi }{. }n_{{{\text{RRP}}}} {. }P_{{{\text{rel}}}} }}{{{\text{D}}_{{{\text{DA}}}} }}\int\limits_{{x_{i} }}^{{x_{j} }} {\left[ {\mu_{1} u^{(e)} + \mu_{2} } \right]{\text{ d}}x} $$

(39)

$$ I_{e2}^{(e)} = \frac{{V_{\max } }}{{D_{{{\text{DA}}}} }}\int\limits_{{x_{i} }}^{{x_{j} }} {\left[ {\beta_{1} v^{(e)} + \beta_{2} )} \right]{\text{ d}}x} $$

(40)

The various parameters are determined by linearization of nonlinear [Ca²⁺] and dopamine mechanisms $\alpha , \, \gamma , \, \kappa , \, \eta , \, \mu_{1} , \, \mu_{2} , \, \beta_{1} ,{\text{ and }}\beta_{2}$. The equations are analyzed, and boundary conditions are added to get the following system of equations.

$$ \frac{{{\text{d}}I_{1} }}{{{\text{d}}\overline{u}^{(e)} }} \,\,=\,\, \sum\limits_{e = 1}^{N} {\overline{Q}^{(e)} } \frac{{{\text{d}}I_{1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }}\overline{Q}^{{(e)^{T} }} = 0 $$

(41)

$$ \frac{{{\text{d}}I_{2} }}{{{\text{d}}\overline{v}^{(e)} }} \,\,=\,\, \sum\limits_{e = 1}^{N} {\overline{Q}^{(e)} } \frac{{{\text{d}}I_{2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }}\overline{Q}^{{(e)^{T} }} = 0 $$

(42)

where

$$ {\overline{\text{Q}}}^{{\text{(e)}}} \,\, = \,\, \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0} \\ {\begin{array}{*{20}c} {.} \\ {\begin{array}{*{20}c} {0} \\ {1} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0} \\ {0} \\ \end{array} } \\ {\begin{array}{*{20}c} {.} \\ {0} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {0} \\ {\begin{array}{*{20}c} {.} \\ {\begin{array}{*{20}c} {0} \\ {0} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1} \\ {0} \\ \end{array} } \\ {\begin{array}{*{20}c} {.} \\ {0} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\;{\text{and}}\;\overline{u} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \\ {u_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} . \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ {u_{19} } \\ \end{array} } \\ {u_{20} } \\ \end{array} } \\ {u_{21} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right],\overline{v} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{1} } \\ {v_{2} } \\ \end{array} } \\ {v_{3} } \\ \end{array} } \\ {\begin{array}{*{20}c} . \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ {v_{19} } \\ \end{array} } \\ {v_{20} } \\ \end{array} } \\ {v_{21} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$

(43)

$$ \frac{{{\text{d}}I_{1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }}\,\, =\,\, \frac{{{\text{d}}I_{a1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} + \frac{{\text{d}}}{{{\text{d}}t}}\frac{{{\text{d}}I_{b1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} + \frac{{{\text{d}}I_{c1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} + \frac{{{\text{d}}I_{{{\text{d}}1}}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} + \frac{{{\text{d}}I_{e1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} + \frac{{{\text{d}}I_{f1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} - \frac{{{\text{d}}I_{g1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} - \frac{{{\text{d}}I_{h1}^{(e)} }}{{{\text{d}}\overline{u}^{(e)} }} $$

(44)

$$ \frac{{{\text{d}}I_{2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} \,\,=\,\, \frac{{{\text{d}}I_{a2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} + \frac{{\text{d}}}{{{\text{d}}t}}\frac{{{\text{d}}I_{b2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} + \frac{{{\text{d}}I_{c2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} + \frac{{{\text{d}}I_{{{\text{d}}2}}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} - \frac{{{\text{d}}I_{e2}^{(e)} }}{{{\text{d}}\overline{v}^{(e)} }} $$

(45)

$$ \left[ A \right]_{42 \times 42} \left[ {\begin{array}{*{20}c} {\left[ {\frac{{\partial \overline{u}}}{\partial t}} \right]_{21 \times 1} } \\ {\left[ {\frac{{\partial \overline{v}}}{\partial t}} \right]_{21 \times 1} } \\ \end{array} } \right] + \left[ B \right]_{42 \times 42} \left[ {\begin{array}{*{20}c} {\left[ {\overline{u}} \right]_{21 \times 1} } \\ {\left[ {\overline{v}} \right]_{21 \times 1} } \\ \end{array} } \right] = [F]_{42 \times 1} $$

(46)

The time derivatives in the finite element techniques were solved by Crank–Nicolson scheme for system matrices (A and B) and system vectors (F).