Black holes in Einstein–Gauss–Bonnet gravity with a background of modified Chaplygin gas

Abstract

Supposing the existence of modified Chaplygin gas with the equation of state $p=A\rho -B/\rho ^\beta$ as a cosmic background, we obtain a static spherically symmetric solution to the Einstein–Gauss–Bonnet gravitational equations in 5D spacetime. The spacetime structure of the obtained black hole solution could be asymptotically anti-de Sitter or de Sitter, according to the specific values of modified Chaplygin gas parameters versus the cosmological constant. We analyze the parametric regions for both kinds of solutions. For asymptotically anti-de Sitter black hole, there exists the so-called small/large black hole phase transition, and we obtain critical values of pressure, volume and temperature and investigate the effects of both the Gauss–Bonnet gravity and the modified Chaplygin gas on these values. For asymptotically de Sitter black hole, no $P-r_{\mathrm{h}}$ criticality and phase transition appear, and we show that the thermodynamic systems related to various horizons of asymptotically de Sitter black hole are in fact entangled.

A Einstein–Gauss–Bonnet black holes in D-dimensional spacetime

The energy density of the modified Chaplygin gas shows

$$\begin{aligned} \rho (r)=\left[ \frac{1}{1+A}\left( B+\left[ \frac{Q}{r^{D-1}}\right] ^{(1+A)(1+\beta )}\right) \right] ^{\frac{1}{1+\beta }}. \end{aligned}$$

(38)

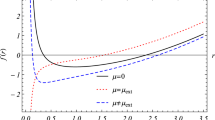
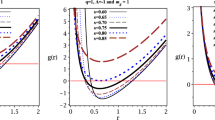
The solution for the metric function is obtained as

$$\begin{aligned} f_{\pm }(r) = \kappa +\frac{r^{2}}{2{\alpha }(D-3)(D-4)}\left( 1\pm \sqrt{{\mathcal {H}}}\right) \end{aligned}$$

(39)

with

$$\begin{aligned} {\mathcal {H}} & = 1+\frac{4\alpha (D-3)(D-4)}{D-2}\left[ \frac{2 M}{\Sigma _{D-2}r^{D-1}}+\frac{2\Lambda }{D-1} +\frac{2}{D-1}\Big (\frac{B}{1+A}\Big )^{\frac{1}{1+\beta }}{\mathcal {F}}\right] ,\nonumber \\ {\mathcal {F}} & = \, _{2}F_{1}\left( \left[ -\frac{1}{1+\beta },-\frac{1}{w}\right] ,1-\frac{1}{w}, -\frac{1}{B}\left( \frac{Q}{r^{D-1}}\right) ^{w}\right) ,\nonumber \\ w & = (1+A)(1+\beta ), \end{aligned}$$

(40)

where $\Sigma _{D-2}$ denotes the volume of the unit $(D-2)$ sphere. Again, only the minus branch solution $f_{-}(r)$ is considered as a black hole solution.

The black hole horizon $r_{\mathrm{h}}$ for asymptotically anti-de Sitter solutions satisfies $f_-(r_{\mathrm{h}})=0$, while the black hole horizon $r_{\text {b}}$, cosmological horizon $r_c$ and inner horizon $r_i$ for asymptotically de Sitter solutions satisfy the equation $f_-(r_{b,c,i})=0$. The ADM mass of the black hole in terms of the several horizons reads

$$\begin{aligned} \begin{aligned} M&=\frac{\Sigma _{D-2}}{2}\left[ (D-2)r_{h,b,c,i}^{D-3}\kappa +(D-2)(D-3)(D-4)r_{h,b,c,i} ^{D-5}\alpha \kappa ^2-\frac{2\Lambda }{D-1}r_{h,b,c,i}^{D-1} \right. \\& \quad \left. -\frac{2r_{h,b,c,i}^{D-1}}{D-1}\left( \frac{B}{1+A}\right) ^{\frac{1}{1+\alpha }} {\mathcal {F}}(r_{h,b,c,i})\right] . \end{aligned} \end{aligned}$$

(41)

According to Eq. (41), the three horizons of asymptotically de Sitter black hole are entangled. The Hawking temperatures associated with different horizons are calculated as

$$\begin{aligned}&T_{h,b}=\frac{r_{h,b}}{4\pi {\mathcal {N}}(r_{h,b})}\left[ (D-5)\kappa +(D-3)(D-4)(D-5)\frac{\alpha \kappa ^2}{r_{h,b}^2} +2\kappa -\frac{2}{D-2}r_{h,b}^2(\Lambda +\rho (r_{h,b}))\right] , \end{aligned}$$

(42)

$$\begin{aligned}&T_{c,i}=\frac{-r_{c,i}}{4\pi {\mathcal {N}}(r_{c,i})}\left[ (D-5)\kappa +(D-3)(D-4)(D-5) \frac{\alpha \kappa ^2}{r_{c,i}^2}+2\kappa -\frac{2}{D-2}r_{c,i}^2(\Lambda +\rho (r_{c,i}))\right] , \end{aligned}$$

(43)

with

$$\begin{aligned} {\mathcal {N}}(r_{h,b,c,i})=r_{h,b,c,i}^2+2(D-3)(D-4)\alpha \kappa . \end{aligned}$$

The entropies are given by

$$\begin{aligned} S_{h,b,c,i}=2\pi (D-2)\Sigma _{D-2}r_{h,b,c,i}^{D-4}\left[ \frac{r_{h,b,c,i}^2}{D-2}+2(D-3)\alpha \kappa \right] . \end{aligned}$$

(44)

The Gibbs free energies related to different horizons are identified as

$$\begin{aligned}&G_{h,b}=M-T_{h,b}S_{h,b}, \end{aligned}$$

(45)

$$\begin{aligned}&G_{c,i}=-M-T_{c,i}S_{c,i}. \end{aligned}$$

(46)