Light beam interacting with electron medium: exact solutions of the model and their possible applications to photon entanglement problem

Abstract

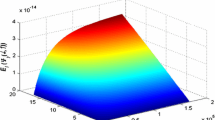
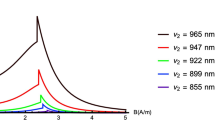
We consider a model for describing a QED system consisting of a photon beam interacting with quantized charged spinless particles. We restrict ourselves by a photon beam that consists of photons with two different momenta moving in the same direction. Photons with each moment may have two possible linear polarizations. The exact solutions correspond to two independent subsystems, one of which corresponds to the electron medium and another one is described by vectors in the photon Hilbert subspace and is representing a set of some quasi-photons that do not interact with each other. In addition, we find exact solution of the model that correspond to the same system placed in a constant magnetic field. As an example, of possible applications, we use the solutions of the model for calculating entanglement of the photon beam by quantized electron medium and by a constant magnetic field. Thus, we calculate the entanglement measures (the information and the Schmidt ones) of the photon beam as functions of the applied magnetic field and parameters of the electron medium.

Appendix A: Entanglement in two-qubit systems

We recall that a qubit is a two-level quantum-mechanical system with the Hilbert space ${\mathcal {H}}={\mathbb {C}}^{2}$. Vectors in the space ${\mathcal {H}}$ are two columns $\left| \psi \right\rangle =(\psi _{1},\psi _{2})^{T}$. The scalar product reads: $\langle \psi ^{\prime }\left| \psi \right\rangle =\psi _{1}^{\prime *}\psi _{1}+\psi _{2}^{\prime *}\psi _{2}$. An orthogonal basis $\left| a\right\rangle$, $a=0$, 1 in ${\mathcal {H}}$ can be chosen as: $\left| 0\right\rangle =(1,0)^{T}$, $\left| 1\right\rangle =(0,1)^{T}$, $\langle a\left| a^{\prime }\right\rangle =\delta _{aa^{\prime }}$, $\sum _{a=0,1}\left| a\right\rangle \langle a\mid \ = I$, where I is $2\times 2$ unit matrix.

Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two states can be taken to be the vertical polarization and the horizontal polarization.

Let us consider a system, composed of two qubit subsystems A and B with the Hilbert space ${\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}$ where ${\mathcal {H}}_{A}={\mathbb {C}}^{2}\$and ${\mathcal {H}}_{B}={\mathbb {C}}^{2}$. The composite system is a four level and is also called the two-qubit system. If $\left| a\right\rangle _{A}$ and $\left| b\right\rangle _{B}$, a, $b=0$, 1, are orthonormal bases in the spaces ${\mathcal {H}}_{A}$ and ${\mathcal {H}}_{B}$, respectively, then $\left| \alpha b\right\rangle =\left| a\right\rangle \otimes \left| b\right\rangle$ is a complete and orthonormalized bases in ${\mathcal {H}}_{AB}$, which is called computational bases,

$$\begin{aligned}&\ \left| \alpha b\right\rangle =\left| a\right\rangle \otimes \left| b\right\rangle =\left( a_{1}b_{1},a_{1}b_{2},a_{2} b_{1},a_{2}b_{2}\right) ^{T}\,, \\& \langle \alpha b\left| \alpha ^{\prime }b^{\prime }\right\rangle =\delta _{\alpha \alpha ^{\prime }}\delta _{bb^{\prime }}\ ,\ \sum _{\alpha ,b=0,1}\left| \alpha b\right\rangle \langle \alpha b\mid \ ={\mathbf {I}}\,. \end{aligned}$$

where ${\mathbf {I}}$ is $4\times 4$ unit matrix. The vectors of the computational bases are eigenstates of the operator $\sigma _{z}\otimes \sigma _{z}=\mathrm {diag}(1,-1,-1,1)$, namely $\left[ \sigma _{z}\otimes \sigma _{z}\right] \left| aa^{\prime }\right\rangle = (-1)^{(a+a^{\prime })}\left| aa^{\prime }\right\rangle$. The basis is often denoted as $\left| \Theta \right\rangle _{s}$,$\ s=1,2,3,4$,

$$\begin{aligned} \left| \Theta \right\rangle _{1}&=\left| 00\right\rangle =\left( \begin{array}{cccc} 1&0&0&0 \end{array} \right) ^{T},\ \ \left| \Theta \right\rangle _{2}=\left| 01\right\rangle =\left( \begin{array}{cccc} 0&1&0&0 \end{array} \right) ^{T}\ ,\nonumber \\ \left| \Theta \right\rangle _{3}&=\left| 10\right\rangle =\left( \begin{array}{cccc} 0&0&1&0 \end{array} \right) ^{T},\ \ \left| \Theta \right\rangle _{4}=\left| 11\right\rangle =\left( \begin{array}{cccc} 0&0&0&1 \end{array} \right) ^{T}\,. \end{aligned}$$

(A1)

A pure state $\left| \Psi \right\rangle _{AB}\in {\mathcal {H}}_{AB}$ is called separable if and only it can be represented as $\left| \Psi \right\rangle _{AB}=\left| \Psi \right\rangle _{A}\otimes \left| \Psi \right\rangle _{B}$, $\left| \Psi \right\rangle _{A}\in {\mathcal {H}}_{A}$,$\ \left| \Psi \right\rangle _{B}\in {\mathcal {H}}_{B}$. Respectively, a state $\left| \Psi \right\rangle _{AB}$ is entangled if it is not separable.

A measure of the entanglement is a real positive number $E(\left| \Psi \right\rangle _{AB})\in {\mathbb {R}}_{+}$ which is assigned to each state $\left| \Psi \right\rangle _{AB}$. The measure of entanglement is zero for separable states and assumes its maximum 1 for maximally entangled states.

An entanglement measure $E(\left| \Psi \right\rangle _{AB})$ of a state $\left| \Psi \right\rangle _{AB}$ of a two-qubit system was proposed by Bennett in Ref. [28]. It reads³:

$$\begin{aligned}&E\left( \left| \Psi \right\rangle _{AB}\right) =S\left( \hat{\rho }_{A}\right) =S\left( {\hat{\rho }}_{B}\right) \ ,\nonumber \\&S\left( {\hat{\rho }}_{A}\right) =-\mathrm {tr}\left( {\hat{\rho }}_{A}\log {\hat{\rho }}_{A}\right) ,\ \ S\left( {\hat{\rho }}_{B}\right) =-\mathrm {tr} \left( {\hat{\rho }}_{B}\log {\hat{\rho }}_{B}\right) \,, \end{aligned}$$

(A2)

where $S({\hat{\rho }}_{A})$ is von Neumann entropy of a statistical operator ${\hat{\rho }}_{A}$ of the subsystem A, whereas $S({\hat{\rho }}_{B})$ is von Neumann entropy of the statistical operator ${\hat{\rho }}_{B}$ of the subsystem B (one can see that $S(\rho _{A})=S(\rho _{B})$). For a pure state $\left| \Psi \right\rangle _{AB}$, we have:

$$\begin{aligned}&{\hat{\rho }}_{A}=\mathrm {tr}_{B}{\hat{\rho }}_{AB}=\sum _{b}\langle b\left| {\hat{\rho }}_{AB}\mid b\right\rangle \,,\\&{\hat{\rho }}_{B}=\mathrm {tr}_{A}{\hat{\rho }}_{AB}= \sum _{a}\langle a\left| {\hat{\rho }}_{AB}\mid a\right\rangle ,\quad {\hat{\rho }}_{AB}=\ _{AB}\mid \Psi \rangle \langle \Psi \mid _{AB}. \end{aligned}$$

In the case of a pure state, its reduced statistical operators have nonzero quantum entropy, whereas the entropy of the initial pure state is always zero. By definition, a pure state of a two-qubit system is maximally entangled if its reduced statistical operators are proportional to the identity operators.

Let us decompose the state $\left| \Psi \right\rangle _{AB}$ and the operator ${\hat{\rho }}_{AB}$ in the computational bases,

$$\begin{aligned} \left| \Psi \right\rangle _{AB}&=\sum _{s=1}^{4}\upsilon _{s}\left| \Theta \right\rangle _{s}\\&\Longrightarrow {\hat{\rho }}_{AB}=\left[ \upsilon _{1}\left| 00\right\rangle +\upsilon _{2}\left| 01\right\rangle +\upsilon _{3}\left| 10\right\rangle +\upsilon _{4}\left| 11\right\rangle \right] \\&\quad \quad \times \left[ \upsilon _{1}^{*}\langle 00\mid +\upsilon _{2}^{*}\langle 01\mid +\upsilon _{3}^{*}\langle 10\mid +\upsilon _{4}^{*} \langle 11\mid \right] \,. \end{aligned}$$

Then, with account taken of the relations

$$\begin{aligned}&\left| 0\right\rangle \langle 0\mid \ =\mathrm {diag}\left( 1,0\right) ,\qquad \,\,\,\, \left| 1\right\rangle \langle 1\mid \ =\mathrm {diag}\left( 0,1\right) \,,\\&\left| 0\right\rangle \langle 1\mid \ =\mathrm {antidiag}\left( 1,0\right) ,\quad \left| 1\right\rangle \langle 0\mid =\mathrm {antidiag}\left( 0,1\right) \,, \end{aligned}$$

where states $\left| a\right\rangle$ basis vectors in the Hilbert space ${\mathcal {H}}_{A}$, we obtain:

$$\begin{aligned} {\hat{\rho }}_{A}&=\, _{B}\langle 0\mid {\hat{\rho }}_{AB}\left| 0\right\rangle _{B}+\ _{B}\langle 1\mid {\hat{\rho }}_{AB}\left| 1\right\rangle _{B} \\&= \mid \upsilon _{1}\mid ^{2}\left| 0\right\rangle \langle 0\mid +\upsilon _{1} \upsilon _{3}^{*}\left| 0\right\rangle \langle 1\mid +\mid \upsilon _{2} \mid ^{2}\left| 0\right\rangle \langle 0\mid +\upsilon _{2}\upsilon _{4}^{*}\left| 0\right\rangle \langle 1\mid \\&\quad +\upsilon _{3}\upsilon _{1}^{*}\left| 1\right\rangle \langle 0\mid +\mid \upsilon _{3}\mid ^{2}\left| 1\right\rangle \langle 1\mid +\upsilon _{4} \upsilon _{2}^{*}\left| 1\right\rangle \langle 0\mid +\mid \upsilon _{4} \mid ^{2}\left| 1\right\rangle \langle 1\mid \ =\left( \begin{array}{ll} \rho _{11}^{\left( A\right) } & \rho _{12}^{\left( A\right) }\\ \rho _{21}^{\left( A\right) } &{} \rho _{22}^{\left( A\right) } \end{array} \right) ,\\ \rho _{11}^{\left( A\right) }&=\mid \upsilon _{1}\mid ^{2}+\mid \upsilon _{2}\mid ^{2} ,\ \rho _{12}^{\left( A\right) }=\upsilon _{1}\upsilon _{3}^{*}+\upsilon _{2}\upsilon _{4}^{*}\ ,\\ \rho _{21}^{\left( A\right) }&=\upsilon _{3}\upsilon _{1}^{*}+\upsilon _{4}\upsilon _{2}^{*},\ \ \rho _{22}^{\left( A\right) }=\mid \upsilon _{3}\mid ^{2}+\mid \upsilon _{4}\mid ^{2}\,. \end{aligned}$$

Calculating the entanglement measure, we can use eigenvalues of the matrix ${\hat{\rho }}_{A}$,

$$\begin{aligned}&{\hat{\rho }}^{\left( A\right) }P_{a}=\lambda _{a}P_{a},\ \ \lambda _{a} =\frac{1}{2}\left[ \rho _{11}^{\left( A\right) }+\rho _{22}^{\left( A\right) }+\left( -1\right) ^{a}y\right] ,\ a=1,2;\nonumber \\&P_{a}=\left( \begin{array}{c} \frac{\rho _{11}^{\left( A\right) }-\rho _{22}^{\left( A\right) }+\left( -1\right) ^{a}y}{2\rho _{21}^{\left( A\right) }}\\ 1 \end{array} \right) ,\ y=\root + \of {\left( \rho _{11}^{\left( A\right) }-\rho _{22}^{\left( A\right) }\right) ^{2}+4\left| \rho _{12}^{\left( A\right) }\right| ^{2}}\nonumber \\&\quad =\sqrt{\left( \mid \upsilon _{1}\mid ^{2}+\mid \upsilon _{2}\mid ^{2}-\mid \upsilon _{4} \mid ^{2}-\mid \upsilon _{3}\mid ^{2}\right) ^{2}+4\left| \upsilon _{1}\upsilon _{3}^{*}+\upsilon _{2}\upsilon _{4}^{*}\right| ^{2}}\,. \end{aligned}$$

(A3)

Thus, we obtain

$$\begin{aligned} E\left( \Psi \right) =-\sum _{a=1,2}\lambda _{a}\log _{2}\lambda _{a}=-\left[ z\log _{2}z+\left( 1-z\right) \log _{2}(1-z)\right] ,\ \ z=\frac{1+y}{2}, \end{aligned}$$

and by convention we adopt that $0\log _{2}0\equiv 0$ (see, e.g., Ref. [11]).

It is also known that for a pure two-qubit state one can recognize entanglement by evaluating the so-called Schmidt measure $E_{\mathrm {S}}(\Psi )$, which is the trace of the squared reduced density operators,

$$\begin{aligned} E_{\mathrm {S}}(\Psi )&=1-\mathrm {tr}\left[ \left( {\hat{\rho }}^{(1)}\right) ^{2}\right] =1-\sum _{a=1,2}^{2}\lambda _{a}^{2}\nonumber \\&= 1-\left[ \left( \rho _{11}^{\left( A\right) }\right) ^{2}+\left( \rho _{22}^{\left( A\right) }\right) ^{2}+2\left| \rho _{12}^{\left( A\right) }\right| ^{2}\right] \,. \end{aligned}$$

(A4)

The Schmidt measure can be considered as an alternative to the information entanglement measure.