Skip to main content
SpringerLink
Log in

Protection of qubits by nonlinear resonances

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

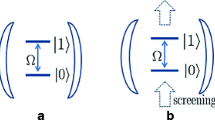
We show that quantized superconducting circuits are non-integrable at the classical level of description, adorned by nonlinear resonances amidst stochastic sea. The stable (elliptic) and unstable (hyperbolic) points occur in a way that by choosing the parameters of a system close to elliptic points, the dynamics is stable. Quantum mechanically, any disturbance has to tunnel the separatrix to reach the elliptic point. Thus, nonlinearity of the system provides protection. Based on these fundamental considerations from the Kolmogorov–Arnold–Moser theorem, we propose criteria for protection of qubits from any disturbance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Article Open access 12 November 2022

Eric Hyyppä, Suman Kundu, … Mikko Möttönen

Data Availability

This manuscript has associated data in a data repository. [Authors’ comment: All data included in this manuscript are available upon reasonable request by contacting with the corresponding author].

References

  1. P. Krantz, M. Kjaergaard, F. Yan, T.P. Orlando, S. Gustavsson, W.D. Oliver, Appl. Phys. Rev. 6, 021218 (2019)

    Article  Google Scholar 

  2. S. Haroche, M. Brune, J.M. Raimond, Nat. Phys. 16, 243 (2020)

    Article  Google Scholar 

  3. A.Y. Kitaev, A. Shen, M.N. Bravyi, Classical and Quantum Computation (American Mathematical Society, Providence, 2002)

    Book  Google Scholar 

  4. Y. Nakamura, Y.A. Pashkin, J.-S. Tsai, Nature 398, 786 (1999)

    Article  ADS  Google Scholar 

  5. J.M. Martinis, M.H. Devoret, J. Clarke, Nat. Phys. 16, 234 (2020)

    Article  Google Scholar 

  6. S.M. Girvin, Quantum Machines: Measurement and Control of Engineered Quantum Systems (Les Houches Summer School, Session XCVI). pp. 113–255 (2014)

  7. Y. Nakamura, Y.A. Pashkin, J.-S. Tsai, Phys. Rev. Lett. 87, 246601 (2001)

    Article  ADS  Google Scholar 

  8. M.V. Berry, Regular and Irregular Motion, ed. by S. Jorna AIP Conference Proceedings, pp. 16–120 (1978)

  9. F. Haake, Quantum Signatures of Chaos (Springer, Heidelberg, 1991)

    MATH  Google Scholar 

  10. H.-J. Stöckmann, Quantum Chaos: An Introduction (Cambridge University Press, New Delhi, 2000)

    MATH  Google Scholar 

  11. N. Jha, S.R. Jain, in AIP Conference Proceedings. American Institute of Physics, vol. 1619, no. 1 (2014)

  12. M.L. Mehta, Random Matrices, 3rd edn. (Academic Press, Amsterdam, 2004)

    MATH  Google Scholar 

  13. V.I. Arnold, Mathematical Methods of Classical Mechanics (Springer, Heidelberg, 1978)

    Book  Google Scholar 

  14. A.J. Lichtenberg, M.A. Lieberman, Regular and Stochastic Motion (Springer, Heidelberg, 1983)

    Book  Google Scholar 

  15. J. Wisdom, Icarus 56, 51 (1983)

    Article  ADS  Google Scholar 

  16. J. Wisdom, Icarus 63, 272 (1985)

    Article  ADS  Google Scholar 

  17. M.A. Nielsen, I. Chuang, Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, 2016)

    MATH  Google Scholar 

  18. J. Preskill, Quantum 2, 79 (2018)

    Article  Google Scholar 

  19. S.R. Jain, R. Samajdar, Rev. Mod. Phys. 89, 045005 (2017)

    Article  ADS  Google Scholar 

  20. S.R. Jain, Phys. Rev. Lett. 70, 3553 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  21. M.C. Gutzwiller, Chaos in Classical and Quantum Mechanics (Springer-Verlag, New York, 1990)

    Book  Google Scholar 

  22. C. Berke et al., Transmon platform for quantum computing challenged by chaotic fluctuations. arXiv preprint arXiv:2012.05923 (2020)

  23. S. Richer et al., Phys. Rev. B 96, 174520 (2017)

    Article  ADS  Google Scholar 

  24. P. Brooks, A.Y. Kitaev, J. Preskill, Phys. Rev. A 87, 052306 (2013)

    Article  ADS  Google Scholar 

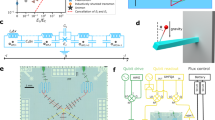
  25. Two capacitively, nonlinearly coupled transmons have two degrees of freedom, possessing two frequencies. The frequencies are functions of action variables, their rational ratios present nonlinear resonances. Presence of such a resonance modifies the phase space in an interesting way, with a chain of stable (elliptic) and unstable (hyperbolic) fixed points, owing to the celebrated Poincaré-Birkhoff theorem [14]

  26. A.I. Neishtadt, J. Appl. Math. Mech. 39, 594 (1975)

  27. J.L. Tennyson, J.R. Cary, D.F. Escande, Phys. Rev. Lett. 56, 2117 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  28. S. Löck, A. Bäcker, R. Ketzmerick, P. Schlagheck, Phys. Rev. Lett. 104, 114101 (2010)

    Article  ADS  Google Scholar 

  29. A. Bäcker, R. Ketzmerick, A.G. Monastra, Phys. Rev. Lett. 94, 054102 (2005)

    Article  ADS  Google Scholar 

  30. A. Gyenis, P.S. Mundada, A. Di Paolo, T.M. Hazard, X. You, D.I. Schuster, J. Koch, A. Blais, A. Houck, PRX Quantum 2, 010339 (2021)

    Article  Google Scholar 

  31. N. Didier, E.A. Sete, M.P. da Silva, C. Rigetti, Phys. Rev. A 97, 022330 (2018)

    Article  ADS  Google Scholar 

  32. G. Rajpoot, K. Kumari, S. Joshi, S.R. Jain, The tunable \(0-\pi \) qubit: dynamics and Relaxation. Int. J. Quantum Inf. 20, 2150032 (2021)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors thank Nishchal R. Dwivedi and Sandeep Joshi for stimulating discussions.

Author information

Authors and Affiliations

  1. Department of Physics and Astronomy, Macquarie University, Sydney, NSW, 2122, Australia

    Rakesh Kumar Saini

  2. Nuclear Physics Division, Bhabha Atomic Research Centre, Mumbai, 400085, India

    Raman Sehgal

  3. Theoretical Nuclear Physics & Quantum Computing Section, Nuclear Physics Division, Bhabha Atomic Research Centre, Mumbai, 400085, India

    Sudhir R. Jain

  4. Homi Bhabha National Institute, Mumbai, 400094, India

    Sudhir R. Jain

  5. UM-DAE Centre for Excellence in Basic Sciences, Vidyanagari Campus, Mumbai, 400098, India

    Sudhir R. Jain

Authors
  1. Rakesh Kumar Saini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Raman Sehgal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sudhir R. Jain
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sudhir R. Jain.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saini, R.K., Sehgal, R. & Jain, S.R. Protection of qubits by nonlinear resonances. Eur. Phys. J. Plus 137, 356 (2022). https://doi.org/10.1140/epjp/s13360-022-02561-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-022-02561-6

Search

Navigation