Extreme events in a class of nonlinear Duffing-type oscillators with a parametric periodic force

Abstract

Extreme events happen when a system is far from the expectation and normal region, which are common in many practical problems, such as climate and engineering systems. It will affect the accuracy and damage the reliability, or even lead to a collapse of the system. In this work, extreme events are studied in a class of generalized nonlinear Duffing-type oscillators with a parametric periodic force. The occurrence mechanism, description methods and risk of extreme events are discussed. We find that the tail probability of the state response is large when extreme events occur frequently. This indicates that the dynamic structure enables the system to reach a rather far position, for which the varying of the potential function provides a possible underlying explanation for this phenomenon. In addition, the effects of the amplitude and the frequency are investigated to quantify the extreme events. With the metrics of inter-event interval (IEI), mean of IEI, survival probability function, and hazard rate function, the risk of extreme events is characterized. The obtained results not only quantitatively give the characteristics of extreme events in a class of generalized Duffing-type oscillators, but also assess the risk of extreme events, which can provide theoretical guidance for the design and fabrication of micro-electromechanical components.

1 Introduction

Extreme events are common in complex nonlinear systems, such as extreme weather caused by EI Ni$\widetilde{\mathrm{n}}$o/Southern oscillation [1], rogue waves in fluid flows or optical cavity systems [2,3,4,5,6]. They deviate far from the expectation of state responses and beyond the acceptable safety range of systems, i.e., accompanied by abrupt change. Generally, extreme events are featured with rarity, irregularity, heavy tail, self-generation, and self-termination [7, 8], which are mostly caused by transient instabilities. In particular, in micro-electromechanical systems (MEMS), extreme large deformations occasionally occur due to an instability [9, 10], which can result in serious damage of MEMS. It was observed that extreme events may put systems at huge risk. Consequently, risk assessment of extreme events is very important, because it reflects the reliability of systems in some sense. It is of great significance to explore the occurrence mechanisms of extreme events and further assess their risk.

Known routes to extreme events include blowout bifurcation, on-off intermittency [11], riddled basin [12], interior crisis [13,14,15,16], channel-like structures [14], and attractor bubbling [17]. In general, extreme events are strongly associated with the bifurcation and chaos of systems, especially in the critical regime [18,19,20,21,22]. For example, single-sided parallel-plate capacitors exhibit stick-slip dynamics because of discontinuous boundaries, which lead to extreme events [9, 23]. Kingston et al. [13] found that Liénard-type oscillators with a periodic excitation display extreme events due to interior crisis and intermittency. In addition, when extreme events occur, systems are accompanied by some features, which can be used to quantitatively characterize extreme events, such as an increased variance, an enhanced skewness, an increased temporal correlation, and a decreased recovery rate [24]. Sapsis et al. [25] proposed spectral analysis and amplitude to describe extreme events. For dissipative systems, kinetic energy and energy dissipation rate can be used as indicators to portray extreme events. Biggs et al. [26] used the spectral density ratio as an indicator for the regime shift. Xu et al. [27] found that phase lag and amplitude difference of the system’s response can be used to detect a regime shift. Besides, the potential function can always characterize the change in the energy of systems and offers an effective way to understand the transition behavior of systems [28,29,30].

To determine the risk of extreme events, the probability measure of systems based on damage models is usually derived. Because of their rareness and irregularity [7, 8], coupled with chaos of systems in general, the probability measure of the state response is difficult to analyze [31, 32]. Fortunately, the extreme value theory provides a feasible probability measure for extreme events. It gives the limit laws of extreme values of independent identically distributed sequential samples, and statistical models of the tails can be estimated by the maximum likelihood method [33]. But the extreme value theory is generally available only for stationary stochastic processes [34]. So it is necessary to find a new indicator for statistical modeling or a new statistical modeling method for a large number of complex systems containing intermittent features. The inter-event interval (IEI) is proposed as an important metric that reflects the intrinsic evolutionary pattern of extreme events in the system and is also called the return time [35]. The advantage of this metric is that it is one of the most important indicators reflecting the risks of occurring extreme events in a system. For instance, to describe the risk associated with an earthquake, Hristopulos et al. [35] applied three metrics to assess risk, including the mean of IEI, the survival probability function, and the hazard rate function. Due to the stationarity of the IEI, it is simpler to use IEI for statistical modeling and also to apply its statistical model for risk assessment.

In the present study, we attempt to investigate the risk assessment of extreme events in a class of typical Duffing-type oscillators subjected to a parametric periodic excitation. The rest of this study is organized as follows. Section 2 introduces a class of Duffing-type oscillators and analyzes its state responses. Section 3 observes extreme events and explores their possible mechanisms by means of the potential function. Extreme events in terms of the probability density function (PDF) are portrayed in Sect. 4. Section 5 evaluates the risk of the system based on the IEI. Section 6 concludes the paper.

2 Model

In this section, we consider the following generalized nonlinear Duffing-type oscillator subjected to a parametric periodic excitation

$$\begin{aligned} \ddot{x}+\mu {\dot{x}}+g(x)=A\text {sin}(\omega t) \cdot f(x), \end{aligned}$$

(1)

where $\mu$ is damping coefficient and g(x) is nonlinear stiffness. A and $\omega$ are the amplitude and the frequency of the periodic excitation, respectively. g(x) and f(x) are polynomial functions, where $g(x)=\kappa _{1} x+\kappa _{2} x^{3}$. $f(x)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}$ is used which results from an alternating current voltage in the motion of MEMS [36]. For the convenience of analyzing the model, we rewrite the model as follows.

$$\begin{aligned}&{\dot{x}}=y, \end{aligned}$$

(2a)

$$\begin{aligned}&{\dot{y}}=-\mu y-g(x)+A\text {sin}(\omega t) \cdot f(x). \end{aligned}$$

(2b)

In this work, we focus on the analysis and utilization of extreme events in system (2) when A and $\omega$ vary. As for the first step, the bifurcation diagram is shown in Fig. 1 from the integration of Eq. (2) by the fourth-order Runge–Kutta method. The parameter sets are $\mu =0.03$, $\kappa _{1}=0.108$, $\kappa _{2}=10.216$, $a_{0}=1$, $a_{1}=2$, $a_{2}=3$ and $a_{3}=4$, which keep unchanged unless otherwise stated.

Fig. 1

Bifurcation diagram of system (2), where $A\in [0, 2.55]$, $\mu =0.03$, $\kappa _{1}=0.108$, $\kappa _{2}=10.216$, $\omega =1.0$ and the initial conditions $x_{0}$ = 0.0001 and ${\dot{x}}_{0}$ = 0.0006. Unless otherwise indicated, no change in the initial conditions are done. The blue points and the gray points are the maxima and minima, respectively. The insert is the bifurcation diagram when $A\in [0,2]$. The red dashed lines marked L1, L2, L3 and L4 represent A = 0.1, A = 0.3, A = 1.5 and A = 2.5

As shown, system (2) exhibits a period-doubling bifurcation. Specifically, as A changes from 0 to 3, the system (2) starts from a period-one oscillation, undergoes a period-doubling bifurcation, transforms to multi-period oscillations, and then leads to chaos. It is shown that when A is larger than 2.54, x tends to be infinite, i.e., system (2) diverges. In MEMS, such a phenomenon corresponds to the resonant pull-in instability which may result in a breakdown of the system [37]. Therefore, it is crucial to explore how will the system behave near such a set of parameters. To begin with, the stability can be analyzed by the maximum Lyapunov exponent $\lambda _{1}$ for system (2), which has been calculated in Fig. 2 with respect to A. It shows that $\lambda _{1}$ is negative when A is very small. As A increases, most $\lambda _{1}$ becomes positive, while some $\lambda _{1}$ keeps negative occasionally. As known, when $\lambda _{1}<0$, the system is stable. Chaos occurs with $\lambda _{1}>0$. This is verified by the bifurcation diagram in Fig. 1. Namely, the system (2) performs periodic oscillation for small A when $\lambda _{1}<0$, and chaos for large A when $\lambda _{1}>0$. In the following, we focus on the extreme dynamical behaviors of the system (2) when A closes to 2.54 but remains smaller.

Fig. 2

Maximum Lyapunov exponent $\lambda _{1}$ versus the amplitude A of system (2). The horizontal red dashed line is $\lambda _{1}=0$

3 Extreme events in the oscillator

3.1 Occurrence of extreme events

In this part, based on system (2), we show the state response x under different A. Figure 3 provides the curves of time history and phase diagram under different A. According to Figs. 1 and 2, the system (2) is in a periodic regime when $\lambda _{1}$ is negative for $A<0.6$, while it is chaotic when $\lambda _{1}>0$ for most $A>0.6$. Therefore, for periodic motion, $A=0.1$ and $A=0.3$ are taken as examples, while for chaotic motion, $A=1.5$ and $A=2.5$ are taken as examples.

Fig. 3

Time series x(t) and y(t) of system (2) under different A. (a1) The x and the insert is the x(t) in $t\in [9870, 9900]$. (a2) The y and the insert is the y(t) in $t\in [9870,9900]$. (a3) The phase diagram and the insert is zoomed in. The parameters are (a1)–(a3) A = 0.1, (b1)–(b3) A = 0.3, (c1)–(c3) A = 1.5 and (d1)–(d3) A = 2.5, respectively. The yellow areas in (c1) and (d1) show the marked large-amplitude oscillations. In (a1)–(a3), the system (2) shows a phenomenon of period-one oscillation. In (b1)–(b3), multi-period oscillations occurs in system (2). In (c1)–(c3) and (d1)–(d3), chaos occurs

When A = 0.1, the system (2) exhibits a period-one motion and $\lambda _{1}<0$ in Figs. 2 and 3(a1)–(a3), corresponding to the vertical red dashed line marked L1 in Fig. 1. As A increases, the system (2) changes to multi-period oscillations. Figure 3 (b1)–(b3) shows the curves at A = 0.3, and Fig. 2 shows $\lambda _{1}<0$. The red vertical dashed line marked L2 in Fig. 1. When A = 1.5 and A = 2.5, it is found that chaos occurs and $\lambda _{1}>0$, namely the period-doubling bifurcation moves toward chaos. The vertical red dashed lines marked L3 and L4 in Fig. 1 are A = 1.5 and A = 2.5, respectively. The amplitude of x increases and large-amplitude oscillations occur with the increase in A. The large-amplitude responses are framed in the yellow area in Fig. 3. Such extreme oscillations are generally detrimental to a safe operation of systems. Therefore, it is essential to quantitatively study these extreme behaviors, and introduce indicators to measure their degrees of deviation from the normal state.

Within a certain time interval T, the time set is recorded as $T=\{t_{0},t_{1},\ldots ,t_{N}\}$, and the corresponding state response is recorded as $X=\{x(t_{0}),x(t_{1}),\ldots ,x(t_{N})\}$, where N is the number of sampling points generated in the simulation time T. We introduce two indicators, namely $d_\mathrm{max}$ and $d_\mathrm{min}$ [38,39,40],

$$\begin{aligned} d_\mathrm{max}=\frac{\mathrm{max}(x)-{\bar{x}}}{\sigma }, d_\mathrm{min}=\frac{\mathrm{min}(x)-{\bar{x}}}{\sigma }, \end{aligned}$$

(3)

where $\mathrm{max}(\cdot )$ and $\mathrm{min}(\cdot )$ are the maximum and minimum of the x over the simulation time T, respectively. ${\bar{x}}=\dfrac{1}{N}\sum _{i=1}^Nx(t_{i})$ is the sample mean and $\sigma =\sqrt{\dfrac{1}{N}\sum _{i=1}^N[x(t_{i})-{\bar{x}}]^{2}}$ is the sample standard deviation. The two indicators are mainly used to characterize the magnitude how the amplitude deviates from the mean at the level of $\sigma$. In general, data fluctuates within a small region near the mean. For large amounts of data, according to the Central Limit Theorem and the $3 \sigma$ criteria for Gaussian distribution, about 99.73$\%$ of the data fall within (${\bar{x}}-3 \sigma$, ${\bar{x}}+3 \sigma$). The rest fall outside (${\bar{x}}-3 \sigma$, ${\bar{x}}+3 \sigma$), which is regarded as anomalous data. When data is in the (${\bar{x}}-3 \sigma$, ${\bar{x}}+3 \sigma$), $|d_\mathrm{max}|$ and $|d_\mathrm{min}|$ do not exceed 3. Otherwise, $|d_\mathrm{max}|$ and $|d_\mathrm{min}|$ are greater than 3. For the system (2), $d_\mathrm{max}$ and $d_\mathrm{min}$ are calculated (Fig. 4). We can see that when $A< 2$, the $|d_\mathrm{max}|$ and $|d_\mathrm{min}|$ vary slowly on the whole. When $A\ge 2$, $|d_\mathrm{max}|$ and $|d_\mathrm{min}|$ change abruptly. Eventually, $|d_\mathrm{max}|$ and $|d_\mathrm{min}|$ exceed 3 for large A. It means that the increase in A will result in abnormal data or behaviors. In this work, we assume that when $3\le |d_\mathrm{max}|< 4$ and $3\le |d_\mathrm{min}|< 4$, the system (2) may have some exceptional amplitudes but still operates. However, when $|d_\mathrm{max}|> 4$ and $|d_\mathrm{min}|> 4$, the amplitude is large enough to put the system (2) into a dangerous situation, i.e., having risk of being damaged.

Fig. 4

$d_\mathrm{max}$ and $d_\mathrm{min}$ of the system (2)

Therefore, we define the portions beyond $4\sigma$ as the criteria of extreme events in this work, which is determined by the dynamics of our system. Of course, extreme events are also judged by exceeding $8\sigma$ even $12\sigma$ in other systems [38], which depends on practical analysis of requirements. The thresholds include forward offset and reverse offset, defined as $TS_\mathrm{max}={\bar{x}}+4\sigma$ and $TS_\mathrm{min}={\bar{x}}-4\sigma$, respectively [9, 10, 14]. Therefore, we regard here extreme events occur when $|d_\mathrm{max}|> 4$ and $|d_\mathrm{min}|< 4$ based on our assumption. It follows that the state response x of Fig. 3 does not show extreme events in Fig. 3(c1), while extreme events occur in Fig. 3(d1).

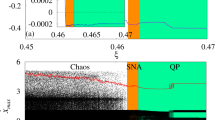
Subsequently, we determine the range of A based on $d_\mathrm{max}$ and $d_\mathrm{min}$. When $A\in$ [0, 2.54], we calculate the thresholds $TS_\mathrm{max}$ and $TS_\mathrm{min}$ under different A and focus on the response beyond the thresholds $TS_\mathrm{max}$ and $TS_\mathrm{min}$. Extreme events are assumed to occur if the maximums exceed the $TS_\mathrm{max}$ or the minimums exceed the $TS_\mathrm{min}$. Therefore, the low value of the maximum value is not used as a reference. Figure 5 shows that the threshold $TS_\mathrm{max}$ and the blue dots in the bifurcation diagram do not intersect at first, and then slowly overlap. When this happens, x has a high probability to exceed the threshold $TS_\mathrm{max}$, i.e., the system (2) may experience extreme events, where A is denoted as $A_\mathrm{critical}$ = 2.41. However, the threshold $TS_\mathrm{min}$ and the gray dots in the bifurcation diagram never intersect, i.e., the system (2) does not exceed $TS_\mathrm{min}$. These results are consistent with Fig. 3, where x is asymmetrical. Thus, the system (2) experiences extreme events when $A\in$ [2.41, 2.54] at $\omega$ = 1.0. We have also chosen multiple sets of initial conditions and found that initial condition had little effect on the statistical properties of extreme events.

Fig. 5

Bifurcation diagram and thresholds $TS_\mathrm{max}$ and $TS_\mathrm{min}$ of the system (2) when $A\in$ [2.3, 2.54]. The blue points are the maximums and the gray points are the minimums. The red curve is $TS_\mathrm{max}$ and the blue curve is $TS_\mathrm{min}$

3.2 Mechanisms of extreme events

In the following, we try to analyze the possible reasons for the generation of extreme events. The potential function plays a crucial role for the dynamics of systems [41, 42]. We first consider the potential function of system (2) in the absence of an external force, which is

$$\begin{aligned} V(x)=\frac{\kappa _{1}}{2}x^2+\frac{\kappa _{2}}{4}x^4. \end{aligned}$$

When $\kappa _{1}>$ 0 and $\kappa _{2}>$ 0, the function V(x) has one equilibrium point at $x=0$, which is the center of the system (2) and is Lyapunov stable. When $\kappa _{1}>$ 0 and $\kappa _{2}<$ 0, $x=0$ is the center and is Lyapunov stable. When $\kappa _{1}<$ 0 and $\kappa _{2}<$ 0, $x=0$ is the saddle point and is Lyapunov unstable. When $\kappa _{1}<$ 0 and $\kappa _{2}>$ 0, $x=0$ is the saddle point and is Lyapunov unstable. For $\kappa _{2}<0$, the potential V(x) is downward and mainly concentrated on the negative potential energy for large |x|. Therefore, x is likely to be infinite under small perturbations of x, which is not stable enough. While for $\kappa _{2}>0$, the potential V(x) is upward, and the potential energy is large for large |x|. Thus, this work only considers $\kappa _{2}>0$. Although $\kappa _{1}$ and $\kappa _{2}$ can lead to monostability or multistability, it can be found that different but interesting phenomena exist [41, 42] for both cases. In fact, monostability or multistability of the system (2) has little effect on extreme events. Therefore, we does not consider the multistability. To be specific, we choose $\kappa _{1}=0.108$ and $\kappa _{2}=10.216$ corresponding to Sect. 2.

In the absence of an external force, the corresponding potential function V(x) is given in Fig. 6(a). It shows that system (2) is constrained by increasing potential energy for large |x|. Consequently, a perturbation on x can only lead a short oscillation around the stable equilibrium point and the system will finally stay still, i.e., the amplitude goes to death. This means that large-amplitude oscillations cannot occur in this situation. However, when the parametric periodic excitation is introduced, the potential function becomes time-varying

$$\begin{aligned} V_{1}(x)=V(x)+A(x+x^2+x^3+x^4)\mathrm{sin}(\omega t). \end{aligned}$$

Fig. 6

Potential function $V_{1}(x)$ of the system (2). (a) When $A=0$, $V_{1}(x)=V(x)$ has a equilibrium point (0, 0); (b) $V_{1}(x)$ when a periodic excitation is considered, in which t = $3\pi /2$ and A takes different values; (c) $V_{1}(x)$ when a periodic excitation is considered, in which A = 2.5 and t take different values

As discussed above, A plays a key role in the occurrence of extreme event. When $A=0$, $V_{1}(x)=V(x)$. Next, we find how A functions in the potential, which provides an intuitional sense how x evolves. Figure 6(b) and (c) shows the potential function $V_{1}(x)$ with respect to different A and t. In Fig. 6(b), for a fixed time t = $3\pi /2$, the variations of $V_{1}(x)$ are shown when A is taken as 0, 2.3, 2.4 and 2.5, respectively. As A increases, the periodic excitation continuously modulates the potential function $V_{1}(x)$. When A is small, $V_{1}(x)$ is always positive and increasing for large x. While for large A, the external excitation is able to induce a decreasing trend at the positive x-axis. Namely, the system will prefer sliding to the positive direction rather than to the negative one. Besides, a larger A produces a smaller $V_{1}(x)$ for the same |x|, which indicates that the system may reach a further place for large A. This corresponds to the bifurcation diagram in Fig. 1 that the larger A , the large is |x|. In Fig. 6(c), for fixed $A = 2.5$, $V_{1}(x)$ are plotted when t is taken as 0, $\pi /6$, $\pi /3$, $\pi /2$, $3\pi /2$, $5\pi /3$ and $11\pi /6$, respectively. It shows that with changing t, $V_{1}(x)$ for $x>0$ oscillates between positive and negative values, while for $x<0$, it is always positive. Thus, it is easy for the system to go far away in the positive direction than in the negative one. This is the reason that the amplitude of the negative x is smaller than the positive one in Figs. 1 and 5. Consequently, we can conclude that for a large A at specific time t when $V_{1}(x)<0$, the system will probably slide to a far place in the positive direction. While with t increasing, $V_{1}(x)$ will increase and push the system back, resulting in the decrease in x. However, because $V_{1}(x)>0$ holds for small negative x, the system will not reach far in the negative direction. This explains the fact that system (2) has extreme events exceeding the $TS_\mathrm{max}$, but not beyond the $TS_\mathrm{min}$.

4 Description of extreme events

To quantitatively measure the properties of extreme event, we investigate the PDF and the probability of extreme events with varying A and $\omega$. As defined, the probability of extreme event corresponds to the tail of the PDF of x exceeding the thresholds $TS_\mathrm{max}$ and $TS_\mathrm{min}$. Therefore, the probability of extreme event is taken as

$$\begin{aligned} P_\mathrm{EE}=\mathrm{Prob}(x\le TS_\mathrm{min} \cup x\ge TS_\mathrm{max}), \end{aligned}$$

which calculates the probability sum of the portions of x exceeding one of the thresholds.

Figure 7 shows the PDFs under different A and $\omega$ = 1.0, corresponding to the red dashed line in Fig. 8. The PDFs in the log–log scale are given in each insert of Fig. 7. The orange and yellow lines are the $TS_\mathrm{max}$ and $TS_\mathrm{min}$, respectively. As shown in Fig. 7, the tail probabilities of the state response x are large, and increases with A. Compared with a specific power-law distribution, the PDFs exhibit roughly a linear scale before the red line, and decrease rapidly for $x>TS_\mathrm{max}$ in Fig. 7(a)–(d). In Fig. 7(e)–(f), when $x>TS_\mathrm{max}$, the PDFs abnormally increase a little and then decrease, which is also found in other systems and called the Dragon Kings phenomenon [43, 44]. This indicates a relatively large fluctuation at the tail of the PDF, which coexists with the power-law distribution and occurs when the power-law is extended to infinity. It is related to the presence of a phase transition and catastrophe at the periphery.

Fig. 7

PDFs of the state response x. The orange and yellow lines represent $TS_\mathrm{max}$ and $TS_\mathrm{min}$, respectively. In each insert, the black dashed line is the PDF in log–log scale, the yellow solid line is the PDF of a specific power-law distribution, and the red solid line is the $TS_\mathrm{max}$

In addition, as for the probability of extreme events, the inset of Fig. 9(a) shows the probability $P_\mathrm{EE}$ when $\omega$ = 1. The larger the A, the higher the probability $P_\mathrm{EE}$ of extreme events, which coincides with the PDFs of Fig. 7. This fact can also be reflected in the state response x, that is, as A increases, the large-amplitude oscillations become more frequent, especially for the amplitudes beyond the thresholds.

When the system is subjected to a periodic excitation, the frequency and amplitude of the excitation are important for the characteristics of extreme events [45, 46]. We explore the effects of the amplitude A and the frequency $\omega$ on extreme events in terms of theirs existence and probability. Regardless of the magnitude of the frequency $\omega$, x always tends to be infinite when A > 2.55. When A = 2.55, the system (2) experiences extreme events only for $\omega \le 0.4$ and the state response x is extremely large. Thus, we restrict the ranges of A and $\omega$ as [0.1, 2.54] and [0.1, 2.0] in this work, respectively. Based on the definition of extreme events in Sect. 3, we give the regions of extreme events in Fig. 8, in which the dark gray regions means that extreme events may occur, while in the light gray regions, no extreme event occurs. It follows that extreme events occur in system (2) when $A>$ 2.35, i.e., the condition for extreme events is that the periodic excitation has a sufficiently large amplitude. Moreover, as A increases, the range of $\omega$ also increases. Besides, when $\omega$ = 0.2, no extreme event happens before A reaching 2. When $\omega$ = 0.4, $A>2.35$ is needed to induce extreme events in the system (2). When $\omega>$ 0.4, it requires a larger and larger A as $\omega$ increases. Since $x<TS_\mathrm{min}$ never happens, we only consider the extreme events of $x>TS_\mathrm{max}$ in the following.

Fig. 8

Dark gray region indicates that some state responses exceed the threshold $TS_\mathrm{max}$, and light gray region indicates that all state responses are within the safe range. That is, extreme events occur in the dark gray region and no one in the light gray region. The region where extreme events occur are mainly in $A>2.41$. The ranges of A and $\omega$ considered in this paper are [2.41, 2.54] and [0.1, 2.0], respectively

According to Fig. 8, the area of extreme events is confirmed. In the following, we quantitatively study the effects of A and $\omega$ on extreme events based on the probability of extreme event $P_\mathrm{EE}$. Figure 9(a) shows $P_\mathrm{EE}$ with respect to A and $\omega$, and Fig. 9(b) shows the contour map. It can be seen that when $\omega$ is fixed, $P_\mathrm{EE}$ increases with the increase in A. When A is fixed, $P_\mathrm{EE}$ increases and then decreases as $\omega$ increases. $P_\mathrm{EE}$ reaches its maximum around $\omega$ = 0.2. Combined with the state response x of system (2), we find that mixed-mode oscillations [14, 16, 47] occur, namely large-amplitude oscillations and small-amplitude oscillations coexist. However, it is surprising that the mean ${\bar{x}}$ and standard deviation $\sigma$ do not change obviously. As a result, the part exceeding the thresholds $TS_\mathrm{max}$ increases, and $P_\mathrm{EE}$ increases. Besides, we find an interesting phenomenon that when $\omega$ = 1.6 and A = 2.53, the system (2) does not experience extreme events, which is unusual.

It follows that the amplitude A and frequency $\omega$ control the existence and characteristics of extreme events. A large A and a small $\omega$ will be helpful for the occurrence of extreme events.

Fig. 9

(a) Probability $P_\mathrm{EE}$ and insert is the probability under $\omega$ = 1.0. (b) Contour map

5 Risk assessment based on extreme events

Extreme event may lead system (2) to be at risk of not working properly or even break down. Therefore, it is necessary to accurately assess the risk of extreme events, i.e., estimate the probability of the state response. For extreme events with rarity and irregularity, the extreme value theory can be used to obtain a probability measure. However, the extreme value theory is only applicable to stationary stochastic processes, which is not satisfied for extreme events with intermittent characteristics [34]. To solve this problem, we apply the inter-event interval for statistical modeling. Rather than the direct analysis of the state response x, IEI focuses on the moment of extreme events, i.e., the temporal behavior. It reflects the inherent evolutionary pattern [14] and is a stationary stochastic process. This is an important property for statistical modeling of systems containing extreme events such as earthquakes [35]. Therefore, in this section, we present the IEI to accurately estimate the probability of extreme events and assess the risk of extreme events. The Weibull distribution for IEI is estimated by the maximum likelihood estimation method, and then indicators are applied to assess the risk.

We first give the definition of the IEI. The set of local extreme values beyond the thresholds is $\{x^{*}_{\tau _{0}},x^{*}_{\tau _{1}},\ldots ,x^{*}_{\tau _{n}}\}, x^{*}_{\tau _{i}}\ge TS_\mathrm{max} \cup x^{*}_{\tau _{i}}\le TS_\mathrm{min}, i = {0,1,\ldots ,n}$, where n is the number of points with local extreme values beyond $TS_\mathrm{max}$ and $TS_\mathrm{min}$, and $\tau _{i}$ is the time corresponding to the ith local extreme event. The IEI sequence of extreme events, i.e., the interval of two adjacent extreme values, is namely $t_\mathrm{IEI}=\{t_{\text {IEI}_{0}},t_{\text {IEI}_{1}},\ldots ,t_{\text {IEI}_{n-1}}\}, t_{\text {IEI}_{i}}=\tau _{i+1}-\tau _{i}, i=0,1,\ldots ,n-1$. It can characterize the frequency of extreme events and provides a possibility for further evaluation of its predictability.

Next, to perform risk assessment, it is necessary to fit the PDF of IEI. This problem is solved by applying the maximum likelihood estimate. The Weibull distribution is often used to statistically model the return times of events such as earthquake, which is an effective model for finite-size systems [35]. Therefore, we assume that the IEI sequence of the system (2) obeys the Weibull distribution $W(\xi ,\eta )$ with the two unknown parameters $\xi$ and $\eta$, and the PDF $\varphi (\cdot )$ and distribution function $F(\cdot )$ are given as

$$\begin{aligned} \varphi (t_\mathrm{IEI};\xi ,\eta )=\left\{ \begin{array}{lr} \frac{\xi }{\eta }\left( \frac{t_\mathrm{IEI}}{\eta }\right) ^{\xi -1}\mathrm{exp} \left[ -\left( \frac{t_\mathrm{IEI}}{\eta }\right) ^{\xi }\right] , &{} t_\mathrm{IEI} \ge 0, \\ 0, &{} t_\mathrm{IEI}<0, \end{array} \right. \end{aligned}$$

(4a)

$$\begin{aligned} F(t_\mathrm{IEI};\xi ,\eta )=\left\{ \begin{array}{lr} 1-\mathrm{exp}\left[ -\left( \frac{t_\mathrm{IEI}}{\eta }\right) ^{\xi }\right] , &{} t_\mathrm{IEI} \ge 0, \\ 0, &{} t_\mathrm{IEI}<0. \end{array} \right. \end{aligned}$$

(4b)

Therefore, the likelihood function is obtained as follows:

$$\begin{aligned} L(t_\mathrm{IEI}; \xi ,\eta )=\prod \limits _{i=0}^{n-1} \frac{\xi }{\eta }\left( \frac{t_\mathrm{IEI_{i}}}{\eta }\right) ^{\xi -1}\mathrm{exp}\left[ -\left( \frac{t_\mathrm{IEI_{i}}}{\eta }\right) ^{\xi }\right] . \end{aligned}$$

(5)

Applying the maximum likelihood estimation method, the parameters $\xi$ and $\eta$ for the Weibull distribution are estimated as ${\hat{\xi }}$ and ${\hat{\eta }}$, respectively.

Subsequently, we assess the risk of occurring extreme events with the aid of the metrics, which includes the mean of IEI, the survival probability function, and the hazard rate function. The mean of IEI is defined as the ratio of the total operating time of the system to the total number of occurring extreme events under a given condition, i.e., the average time between two adjacent extreme events. Based on the Weibull distribution, the formula is obtained as follows:

$$\begin{aligned} \left\langle t_\mathrm{IEI} \right\rangle ={\hat{\eta }} \Gamma (1+1/ {\hat{\xi }}), \end{aligned}$$

(6)

where $\left\langle \cdot \right\rangle$ is the mathematical expectation operator and $\Gamma$ is the Gamma function.

The survival probability function of the system is defined as the probability of the system operating without damage in some time interval $t_\mathrm{IEI}$, i.e., the probability of the system operating normally [35]

$$\begin{aligned} R(t_\mathrm{IEI};A,\omega )=1-F(t_\mathrm{IEI})=\mathrm{exp}\left[ -\left( \frac{t_\mathrm{IEI}}{{\hat{\eta }}}\right) ^{{\hat{\xi }}} \right] . \end{aligned}$$

(7)

And the hazard rate function is defined as

$$\begin{aligned} \begin{aligned} h(t_\mathrm{IEI};A,\omega )&=-\frac{R^{'}(t_\mathrm{IEI};A,\omega )}{R(t_\mathrm{IEI};A,\omega )}=\dfrac{{\hat{\xi }}}{{\hat{\eta }}}\left( \dfrac{t_\mathrm{IEI}}{{\hat{\eta }}}\right) ^{{\hat{\xi }}-1}, \end{aligned} \end{aligned}$$

(8)

which represents the probability that extreme events occur within a unit time after a certain moment when the system have no extreme events before a certain moment [35]. Note that ${\hat{\xi }}$ and ${\hat{\eta }}$ in Eqs. (6)–(8) are dependent on A and $\omega$. Therefore, the risk assessment is performed based on fixed A and $\omega$.

We study the risk of occurring extreme events when $A\in$ [2.45, 2.54] and $\omega$ = 1.0. When $A<$ 2.45, the sample of the IEI series is small, and the error of the maximum likelihood estimate is large. We calculate the IEI sequences of system (2) under different A. According to the maximum likelihood estimate, the resulting PDF and the distribution function are obtained, respectively. Figure 10(a) shows the IEI sequence obtained under $A=2.5$, and we compare the histogram of the IEI series with $\varphi (t_\mathrm{IEI};{\hat{\xi }},{\hat{\eta }})$ in Fig. 10(b), which fits well. Therefore, it can be concluded that the IEI series obeys the Weibull distribution. The metrics are calculated by applying Eqs. (6)–(8).

Fig. 10

(a) IEI sequence obtained under A = 2.5, $\omega$ =1.0, $\kappa _{1}$ = 0.108 and $\kappa _{2}$ = 10.216; (b) histogram and the estimated PDF of the Weibull distribution $W(\xi ,\eta )$; (c) mean of IEI $\left\langle t_\mathrm{IEI} \right\rangle$ under different A

Fig. 11

(a) Survival probability function $R(t_\mathrm{IEI};A,\omega )$. $\omega$ = 1.0, $\kappa _{1}$ = 0.108 and $\kappa _{2}$ = 10.216 in a $t_\mathrm{IEI}-A$ plot. The color indicates the survival probability $R(t_\mathrm{IEI};A,\omega )$. (b) Hazard rate function $h(t_\mathrm{IEI};A,\omega )$

Compared with Fig. 9, we find that as A increases, the probability of extreme events $P_\mathrm{EE}$ gradually increases, and the mean of IEI $\left\langle t_\mathrm{IEI} \right\rangle$ decreases, i.e., the average interval of extreme events gradually decreases in Fig. 10(c). It means that extreme events are more and more frequent, i.e., as A increases, system (2) is at a higher risk of experiencing extreme events. As shown in Fig. 11(a), when A is fixed, the survival probability $R(t_\mathrm{IEI};A,\omega )$ gradually decreases as $t_\mathrm{IEI}$ increases. That is, the longer the waiting time for extreme events, the longer the system (2) runs, and the lower the survival probability $R(t_\mathrm{IEI};A,\omega )$. Meanwhile, the larger the A is, the faster the survival probability function $R(t_\mathrm{IEI};A,\omega )$ decreases, which is consistent with the conclusion in Fig. 9 that the larger the A is, the higher the probability $P_\mathrm{EE}$.

The hazard rate functions $h(t_\mathrm{IEI};A,\omega )$ are plotted under different A in Fig. 11(b). We uncover that when A is fixed, the larger the $t_\mathrm{IEI}$, the higher the hazard rate $h(t_\mathrm{IEI};A,\omega )$. That is, the longer the waiting time for extreme events, the longer the system (2) runs, and the greater the hazard rate $h(t_\mathrm{IEI};A,\omega )$ of the system (2). Moreover, the larger A is, the faster $h(t_\mathrm{IEI};A,\omega )$ increases, which is consistent with the fact that the larger the A is, the higher the probability $P_\mathrm{EE}$ in Fig. 9.

From the above three indicators, we can conclude that when A increases, system (2) is more likely to undergo extreme events. Moreover, the longer the system (2) runs, the lower the survival probability of system (2) and the greater its the hazard rate.

6 Conclusions

We have explored extreme events in a class of generalized Duffing-type oscillators with a parametric periodic excitation. First, the bifurcation diagram and the time histories are employed to determine the range of extreme event for amplitude. Thereafter, the potential function with varying amplitude and time is analyzed to uncover the occurrence mechanism of extreme events. Subsequently, the area of extreme events with respect to the periodic parameters amplitude and frequency are given, showing that the area enlarges with increasing amplitude. The pattern of the probability of extreme events is performed in detail. We find that as amplitude increases, the probability of extreme events increases, whereas the probability increases and then decreases when frequency increases. Namely, a large amplitude and a small frequency are beneficial for the occurrence of extreme events. Finally, the risk of occurring extreme events is assessed. As amplitude increases, there is an increased risk in system (2).

These results give us a clear understanding of extreme events and the risk of extreme events in a generalized Duffing-type oscillator. Due to the heavy tail and intermittent characteristics of extreme events, the prediction of extreme events is a major challenge. It is difficult to predict possible extreme events directly based on the state response. Therefore, what metrics to look for and what measures of the system to apply are issues that will be considered in the future.