Skip to main content
SpringerLink
Log in

Propagation of non-stationary kinematic disturbances from a spherical cavity in the pseudo-elastic cosserat medium

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

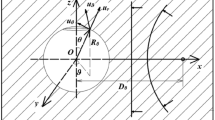
In this work, the Cosserat model is used to simulate non-stationary processes in various structures of composite materials. A non-stationary axisymmetric problem of the propagation of kinematic perturbations from a spherical cavity in a space filled with a homogeneous isotropic pseudo-elastic Cosserat medium is considered. The motion of the medium is represented by a set of three equations written in a spherical coordinate system with the origin at the center of the cavity and nonzero components of the displacement vector and rotation field potentials. At first, it is supposed that the plane wave or spherical wave’s front makes contact with the hollow surface. The initial-boundary value issue is mathematically formulated in dimensionless form. A serial expansion of Legendre and Gegenbauer polynomials, as well as the Laplace transform in time, is utilized to obtain the solution. The issue is simplified to a set of independent ordinary differential equations with the Laplace operator applied to the series coefficients. Due to the complexity of images of the series coefficients, to determine the originals in the linear approximation, the Laurent series for images in the vicinity of the start time is employed. The findings indicate that the solutions found using limit techniques are consistent with previously published results for the classical elastic medium. For the granular composite material of aluminum fractions in the epoxy matrix, examples of computations are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. B. K. Panigrahi, S. K. Sinha, Detection and classification of non-stationary power disturbances in noisy conditions, in 2006 International Conference on Power Electronic, Drives and Energy Systems (2006), pp. 1–5, doi:https://doi.org/10.1109/PEDES.2006.344258

  2. I. Aljamaan, D. Westwick, M. Foley, Non-linear closed-loop identification of CSTR in the presence of a non-stationary disturbances. IFAC-PapersOnLine 48, 1029–1034 (2015). https://doi.org/10.1016/j.ifacol.2015.12.266

    Article  Google Scholar 

  3. E. Cosserat, F. Cosserat, Théorie des corps déformables. Nature 81(2072), 67 (1909). https://doi.org/10.1038/081067a0

    Article  MATH  Google Scholar 

  4. M. Epstein, M. de Leon, Geometrical theory of uniform cosserat media. J. Geom. Phys. 26(1), 127–170 (1998). https://doi.org/10.1016/S0393-0440(97)00042-9

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. H. Ramézani, J. Jeong, Z.-Q. Feng, On parallel simulation of a new linear Cosserat elasticity model with grid framework model assumptions. Appl. Math. Model. 35(10), 4738–4758 (2011). https://doi.org/10.1016/j.apm.2011.03.054

    Article  MathSciNet  MATH  Google Scholar 

  6. J. Till, V. Aloi, D. Rucker, Real-time dynamics of soft and continuum robots based on cosserat-rod models. Int. J. Rob. Res. 38, 723–746 (2019). https://doi.org/10.1177/0278364919842269

    Article  Google Scholar 

  7. P. Neff, A geometrically exact cosserat shell-model including size effects, avoiding degeneracy in the thin shell limit. Part I: formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin. Mech. Thermodyn. 16(6), 577–628 (2004). https://doi.org/10.1007/s00161-004-0182-4

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. J. Altenbach, H. Altenbach, V.A. Eremeyev, On generalized Cosserat-type theories of plates and shells: a short review and bibliography. Arch. Appl. Mech. 80(1), 73–92 (2010). https://doi.org/10.1007/s00419-009-0365-3

    Article  ADS  MATH  Google Scholar 

  9. M. Ostoja-Starzewski, I. Jasiuk, Stress invariance in planar cosserat elasticity. Proc. Math. Phys. Sci. 451(1942), 453–470 (1995). Available: http://www.jstor.org/stable/52637

  10. I. Smolin, R. Bakeev, and P. Makarov, Numerical solution of some two-dimensional problems for an elastoplastic micropolar medium. Vesn. PSTU Math. Model. Syst. Process. 15, 142–155 (2007). Available: https://cyberleninka.ru/article/n/chislennoe-reshenie-nekotoryh-dvumernyh-zadach-dlya-uprugoplasticheskoy-mikropolyarnoy-sredy

  11. V.I. Nikolau, Moment theory of elasticity: development, analysis, and applications (AstroPrint, Odessa, 2006)

    Google Scholar 

  12. V. Erofeev, A. Potapov, Nonlinear longitudinal waves in elastic media with moment stresses. Akust. Zhurnal 37(3), 477–483 (1991). Available: https://ui.adsabs.harvard.edu/abs/1991AkZh...37..477E/abstract

  13. V.I. Erofeev, Propagation of nonlinear shear waves in a solid with microstructure. Int. Appl. Mech. 29(4), 262–266 (1993). https://doi.org/10.1007/BF00847023

    Article  ADS  Google Scholar 

  14. D.Q. Cao, R.W. Tucker, Nonlinear dynamics of elastic rods using the cosserat theory: modelling and simulation. Int. J. Solids Struct. 45(2), 460–477 (2008). https://doi.org/10.1016/j.ijsolstr.2007.08.016

    Article  MATH  Google Scholar 

  15. M. Bîrsan, Several results in the dynamic theory of thermoelastic cosserat shells with voids. Mech. Res. Commun. 33(2), 157–176 (2006). https://doi.org/10.1016/j.mechrescom.2005.08.008

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. R. Kumar, R.R. Gupta, Propagation of waves in transversely isotropic micropolar generalized thermoelastic half space. Int. Commun. Heat Mass Transf. 37(10), 1452–1458 (2010). https://doi.org/10.1016/j.icheatmasstransfer.2010.08.001

    Article  Google Scholar 

  17. I. Nistor, Generalized theory of cosserat thermoelastic media. Bull. Polytech. Inst. Jassy 37, 89–96 (1991). Available: https://scholar.google.com/scholar?cites=10332940448149240274&as_sdt=2005&sciodt=0,5&hl=vi

  18. J. Liu, M. Huang, X.-R. Ge, Solution of stress concentration problem considering influence of couple-stress. J. Shanghai Jiaotong Univ. Chin. Ed 35, 1481–1485 (2001)

    Google Scholar 

  19. R. Kumar, J. Sharma, Reflection of plane waves from the boundaries of a micropolar thermoelastic half-space without energy dissipation. Int. J. Appl. Mech. Eng. 10, 631–645 (2005)

    MATH  Google Scholar 

  20. S.Y. Han, M.N.L. Narasimhan, T.C. Kennedy, Finite crack propagation in a micropolar elastic solid. KSME J. 3(2), 103 (1989). https://doi.org/10.1007/BF02953595

    Article  Google Scholar 

  21. R. Kumar, R. Singh, T.K. Chadha, Eigen value approach to second dynamic problem of micropolar elastic solid. Indian J. Pure Appl. Math. 34, 743–754 (2003)

    MathSciNet  MATH  Google Scholar 

  22. H.S. Saxena and R.S. Dhaliwal, Eigenvalue approach to axially-symmetric coupled micropolar thermoelasticity. Bull. Polish Acad. Sci. Tech. Sci. 38(1), 7–18 (1990). Available: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=4952845

  23. H.N. Nguyen, T.C. Tan, D.T. Luat, V.D. Phan, D. Van Thom, P. Van Minh, Research on the buckling behavior of functionally graded plates with stiffeners based on the third-order shear deformation theory. Materials (Basel) (2019). https://doi.org/10.3390/ma12081262

    Article  Google Scholar 

  24. T.T. Tran, V.K. Tran, P.B. Le, V.M. Phung, V.T. Do, H.N. Nguyen, Forced vibration analysis of laminated composite shells reinforced with graphene nanoplatelets using finite element method. Adv. Civ. Eng. (2020). https://doi.org/10.1155/2020/1471037

    Article  Google Scholar 

  25. V.H. Nam, N.H. Nam, P.V. Vinh, D.N. Khoa, D.V. Thom, P.V. Minh, A new efficient modified first-order shear model for static bending and vibration behaviors of two-layer composite plate. Adv. Civ. Eng. (2019). https://doi.org/10.1155/2019/6814367

    Article  Google Scholar 

  26. D. Van Thom, D.H. Duc, P. Van Minh, N.S. Tung, Finite element modelling for free vibration response of cracked stiffened fgm plates. Vietnam J. Sci. Technol. 58(1), 119 (2020). https://doi.org/10.15625/2525-2518/58/1/14278

    Article  Google Scholar 

  27. N.C. Tho, N.T. Thanh, T.D. Tho, P. Van Minh, L.K. Hoa, Modelling of the flexoelectric effect on rotating nanobeams with geometrical imperfection. J. Braz. Soc. Mech. Sci. Eng. (2021). https://doi.org/10.1007/s40430-021-03189-w

    Article  Google Scholar 

  28. N.T. Dung, P. Van Minh, H.M. Hung, D.M. Tien, The third-order shear deformation theory for modeling the static bending and dynamic responses of piezoelectric bidirectional functionally graded plates. Adv. Mater. Sci. Eng. (2021). https://doi.org/10.1155/2021/5520240

    Article  Google Scholar 

  29. D. Nguyen Thai, P. Van Minh, C. Phan Hoang, T. Ta Duc, N. Nguyen Thi Cam, D. Nguyen Thi, Bending of symmetric sandwich FGM beams with shear connectors. Math. Probl. Eng. (2021). https://doi.org/10.1155/2021/7596300

    Article  MathSciNet  Google Scholar 

  30. V.I. Erofeyev, Wave Processes in Solids with Microstructure (World Scientific, Singabore, 2003)

    Book  Google Scholar 

  31. V. Novatsky, Theory of elasticity (Mir, Moscow, 1975)

    Google Scholar 

  32. E. Aero, E. Kuvshinskii, Basic equations in the theory of elasticity of media with rotation interaction of particles. Fiz. Tverd. Tela 7(2), 1399–1409 (1960). Available: https://scholar.google.com/scholar?hl=vi&as_sdt=2005&sciodt=0,5&cites=16691621741707340366&scipsc=&q=Aero. E.L., Kuvshinskii E.V., Basic equations in the theory of elasticity of media with rotation interaction of particles, Fiz. Tverd. Tela&btnG=

  33. J. Boyd, R. Petschek, The relationships between chebyshev, legendre and jacobi polynomials: the generic superiority of chebyshev polynomials and three important exceptions. J. Sci. Comput. (2014). https://doi.org/10.1007/s10915-013-9751-7

    Article  MathSciNet  MATH  Google Scholar 

  34. G. Lohöfer, Inequalities for Legendre functions and gegenbauer functions. J. Approx. Theory 64(2), 226–234 (1991). https://doi.org/10.1016/0021-9045(91)90077-N

    Article  MathSciNet  MATH  Google Scholar 

  35. G. Bagdasaryan, D. Asanyan, Basic equations and relations of the theory of asymmetric magnetoelasticity of a ferromagnetic body, Problems of the mechanics of thin deformable bodies, in Dedicated to the 80th Anniversary of Academician of the National Academy of Sciences of Armenia SA Ambartsumyan, pp. 37–47 (2002). Available: https://scholar.google.com/scholar?hl=vi&as_sdt=0,5&q=. Nistor, Generalized theory of Cosserat thermoelastic media, Bul. Inst. Politech., Jassy 37, pp. 89–96, 1991.&btnG=

  36. V. Baskakov, N. Bestuzheva, N. Konchakova, Linear dynamic theory of thermoelastic media with a microstructure. Vor. State Tech. Univ. 5–15 (1998). Available: https://scholar.google.com/scholar?q=BaskakovVA%2CBestuzhevaNP%2CKonchakovaNA%282001%29LinearDynamicTheoryofThermoelasticMediawithaMicrostructure%28inRuss.%29

Download references

Acknowledgements

Assoc. Prof. Dr. Nguyen Thai Dung gratefully acknowledges the support of the ministry-level project “Research, design and manufacture torpedo decoy shells for Navy ships.”

Author information

Authors and Affiliations

  1. Faculty of Special Equipment, Le Quy Don Technical University, Hanoi City, 100000, Vietnam

    Lai Thanh Tuan & Nguyen Thai Dung

  2. Faculty of Mechanical Engineering, Le Quy Don Technical University, Hanoi City, 100000, Vietnam

    Do Van Thom & Phung Van Minh

  3. Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O. Box 80203, Jeddah, 21589, Saudi Arabia

    Ashraf M. Zenkour

Authors
  1. Lai Thanh Tuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nguyen Thai Dung
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Do Van Thom
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Phung Van Minh
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ashraf M. Zenkour
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Do Van Thom.

Ethics declarations

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tuan, L.T., Dung, N.T., Van Thom, D. et al. Propagation of non-stationary kinematic disturbances from a spherical cavity in the pseudo-elastic cosserat medium. Eur. Phys. J. Plus 136, 1199 (2021). https://doi.org/10.1140/epjp/s13360-021-02191-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-02191-4

Search

Navigation