Solitons and soliton interactions in repulsive spinor Bose–Einstein condensates with nonzero background

Abstract

We characterize the soliton solutions and their interactions for a system of coupled evolution equations of nonlinear Schrödinger (NLS) type that models the dynamics in one-dimensional repulsive Bose–Einstein condensates with spin one, taking advantage of the representation of such model as a special reduction of a $2\times 2$ matrix NLS system. Specifically, we study in detail the case in which solutions tend to a nonzero background at space infinities. First we derive a compact representation for the multi-soliton solutions in the system using the Inverse Scattering Transform (IST). We introduce the notion of canonical form of a solution, corresponding to the case when the background as $x\rightarrow \infty$ is proportional to the identity. We show that solutions for which the asymptotic behavior at infinity is not proportional to the identity, referred to as being in non-canonical form, can be reduced to canonical form by unitary transformations that preserve the symmetric nature of the solution (physically corresponding to complex rotations of the quantization axes). Then we give a complete characterization of the two families of one-soliton solutions arising in this problem, corresponding to ferromagnetic and to polar states of the system, and we discuss how the physical parameters of the solitons for each family are related to the spectral data in the IST. We also show that any ferromagnetic one-soliton solution in canonical form can be reduced to a single dark soliton of the scalar NLS equation, and any polar one-soliton solution in canonical form is unitarily equivalent to a pair of oppositely polarized displaced scalar dark solitons up to a rotation of the quantization axes. Finally, we discuss two-soliton interactions and we present a complete classification of the possible scenarios that can arise depending on whether either soliton is of ferromagnetic or polar type.

Appendix

1.1 A.1 Unitary transformations, symmetric matrices and rotation of the quantization axes

Recall that the matrix NLS equation (3) is invariant under unitary transformations from the left or from the right. That is, if Q(x, t) solves (3), so does

$$\begin{aligned} {\tilde{Q}}(x,t) = U Q(x,t) V\,, \end{aligned}$$

(A.1)

for all constant U and V such that $U^\dag = U^{-1}$ and $V^\dag = V^{-1}$. On the other hand, in order for ${\tilde{Q}}(x,t)$ to also represent a spinor wave function, the transformation (A.1) must preserve matrix symmetry. That is, one must have ${\tilde{Q}}^\mathrm{T}(x,t) = {\tilde{Q}}(x,t)$ whenever $Q^\mathrm{T}(x,t) = Q(x,t)$. In this appendix we characterize the set of unitary transformations that preserve the symmetry constraint. We also show that all such transformations correspond to a rotation of the quantization axes.

We begin by representing arbitrary unitary matrices U and V without loss of generality in terms of the Pauli matrices as

$$\begin{aligned} U= & {} \exp [ iu_0 I_2 + i{\mathbf {u}}\cdot {\varvec{\sigma }}] = \mathrm{e}^{iu_0} \begin{pmatrix} \cos u + i{\hat{u}}_3\,\sin u &{} i({\hat{u}}_1 - i{\hat{u}}_2)\,\sin u \\ i({\hat{u}}_1 + i{\hat{u}}_2)\,\sin u &{} \cos u - i{\hat{u}}_3\sin u \end{pmatrix}, \end{aligned}$$

(A.2a)

$$\begin{aligned} V= & {} \exp [ iv_0 I_2 + i{\mathbf {v}}\cdot {\varvec{\sigma }}] = \mathrm{e}^{iv_0} \begin{pmatrix} \cos v + i{\hat{v}}_3\,\sin v &{} i({\hat{v}}_1 - i{\hat{v}}_2)\,\sin v \\ i({\hat{v}}_1 + i{\hat{v}}_2)\,\sin v &{} \cos v - i{\hat{v}}_3\sin v \end{pmatrix}, \end{aligned}$$

(A.2b)

where ${\varvec{\sigma }}= (\sigma _1,\sigma _2,\sigma _3)^\mathrm{T}$ is the vector of Pauli matrices, here chosen as

$$\begin{aligned} \sigma _1 = \begin{pmatrix} 0 &{} 1 \\ 1 &{} 0 \end{pmatrix},\quad \sigma _1 = \begin{pmatrix} 0 &{} -i \\ i &{} 0 \end{pmatrix},\quad \sigma _1 = \begin{pmatrix} 1 &{} 0 \\ 0 &{} -1 \end{pmatrix}, \end{aligned}$$

(A.3)

where $u_0$, $v_0$, ${\mathbf {u}} = (u_1,u_2,u_3)^\mathrm{T}$ and ${\mathbf {v}} = (v_1,v_2,v_3)^\mathrm{T}$ are all real, with $\hat{{\mathbf {u}}} = {\mathbf {u}}/u$ and $\hat{{\mathbf {v}}} = {\mathbf {v}}/v$, and where

$$\begin{aligned} u = \sqrt{{\mathbf {u}}\cdot {\mathbf {u}}} = \sqrt{u_1^2 + u_2^2 + u_3^2}\,,\quad v = \sqrt{{\mathbf {v}}\cdot {\mathbf {v}}} = \sqrt{v_1^2 + v_2^2 + v_3^2}\,. \end{aligned}$$

(A.4)

Since $u_0$ and $v_0$ just produce overall phase rotations, without loss of generality we can set $u_0=v_0=0$ owing to the phase invariance of the MNLS equation. Without loss of generality, we can also take u and v in $[0,2\pi ]$.

Inserting (A.2) in (A.1) and requiring the equality of the off-diagonal entries of ${\tilde{Q}}(x,t)$ then yields the following three real constraints:

$$\begin{aligned}&{[} ({\hat{u}}_2{\hat{v}}_3 + {\hat{u}}_3{\hat{v}}_2)\sin u + {\hat{v}}_1 \cos u ]\,\sin v - {\hat{u}}_1\,\sin u \,\cos v = 0\,, \end{aligned}$$

(A.5a)

$$\begin{aligned}&{[} ({\hat{u}}_1{\hat{v}}_3 - {\hat{u}}_3{\hat{v}}_1)\sin u + {\hat{v}}_2 \cos u ]\,\sin v + {\hat{u}}_2\,\sin u\,\cos v = 0\,, \end{aligned}$$

(A.5b)

$$\begin{aligned}&{[} ({\hat{u}}_1{\hat{v}}_2 + {\hat{u}}_2{\hat{v}}_1)\sin u - {\hat{v}}_3 \cos u ]\,\sin v + {\hat{u}}_3\,\sin u\,\cos v = 0\,. \end{aligned}$$

(A.5c)

It is relatively straightforward to see that (A.5) are solved by

$$\begin{aligned} ({\hat{v}}_1,{\hat{v}}_2,{\hat{v}}_3)\,\tan v = ({\hat{u}}_1,-{\hat{u}}_2,{\hat{u}}_3)\,\tan u\,. \end{aligned}$$

(A.6)

In turn, (A.6) implies that (A.5) admit the following inequivalent classes of solutions, obtained respectively when $v = u$ and $v = 2\pi - u$:

$$\begin{aligned} S_+:~({\hat{v}}_1,{\hat{v}}_2,{\hat{v}}_3) = ({\hat{u}}_1, - {\hat{u}}_2, {\hat{u}}_3)\,,\quad S_-:~({\hat{v}}_1,{\hat{v}}_2,{\hat{v}}_3) = (- {\hat{u}}_1, {\hat{u}}_2, - {\hat{u}}_3)\,. \end{aligned}$$

(A.7)

One can now check that $S_+$ implies $V=U^\mathrm{T}$ while $S_-$ implies $V = -U^\mathrm{T}$. Since an overall minus sign can always be rescaled using the phase invariance of the MNLS equation, however, without loss of generality we can limit ourselves to considering only those transformations produced by $S_+$.

Next we show that the unitary transformation (A.1) is equivalent to a complex rotation of the quantization axes. Let ${\mathbf {q}}(x,t) = (q_1, \sqrt{2}\,q_0 , q_{-1})^\mathrm{T}$ be the vector wave functions associated with Q(x, t), and let $\tilde{{\mathbf {q}}}(x,t) = ({\tilde{q}}_1, \sqrt{2}\,{\tilde{q}}_0 , {\tilde{q}}_{-1})^\mathrm{T}$ be the one associated with ${\tilde{Q}}(x,t)$. Observe that a sign change of Q(x, t) obviously translates into a sign change in ${\mathbf {q}}(x,t)$ and recall that, in the quantum-mechanical context, an overall phase of the wave function is immaterial. Therefore, we can again limit ourselves to considering transformations produced by $S_+$. It is straightforward to show that

$$\begin{aligned} \tilde{{\mathbf {q}}}(x,t)= & {} R\,{\mathbf {q}}(x,t)\,, \end{aligned}$$

(A.8a)

where

$$\begin{aligned} R= & {} \begin{pmatrix} c_+^2 &{} \sqrt{2}i({\hat{u}}_1-i{\hat{u}}_2)c_+\sin u &{} - ({\hat{u}}_1-i {\hat{u}}_2)^2\sin ^2u \\ \sqrt{2}i({\hat{u}}_1+i{\hat{u}}_2)c_+\sin u &{}\quad \cos ^2u-(1-2{\hat{u}}_3^2)\sin ^2u &{}\quad \sqrt{2}i({\hat{u}}_1-i{\hat{u}}_2)c_-\sin u \\ - ({\hat{u}}_1+i{\hat{u}}_2)^2\sin ^2u &{}\quad \sqrt{2}i({\hat{u}}_1+i {\hat{u}}_2)c_-\sin u &{}\quad c_-^2 \end{pmatrix},\nonumber \\ \end{aligned}$$

(A.8b)

and where for brevity we defined

$$\begin{aligned} c_\pm= & {} \cos u \pm i {\hat{u}}_3\sin u\,. \end{aligned}$$

(A.8c)

It is also straightforward to check that R is a unitary matrix, i.e., $RR^\dag = R^\dag R = I_3$, and that $\det R = 1$, implying $R\in \mathrm {SU}(3)$. Finally, it is also important to realize that R corresponds to a rotation of the quantization axes. Consider again the transformation (A.1) with $V = U^\mathrm{T}$, and again let $u_0 = 0$ without loss of generality. It is straightforward to show that

$$\begin{aligned} \displaystyle R = \mathrm{e}^{2i{\mathbf {u}}\cdot {\mathbf {f}}}\,, \end{aligned}$$

(A.9)

where ${\mathbf {f}} = (f_1,f_2,f_3)^\mathrm{T}$, and $f_1,f_2,f_3$ are representation of the angular momentum operators in $\mathrm {SU}(3)$, namely:

$$\begin{aligned} f_1 = \frac{1}{\sqrt{2}}\begin{pmatrix}0&{}\quad 1&{}\quad 0\\ 1&{}\quad 0&{}\quad 1\\ 0&{}\quad 1&{}\quad 0 \end{pmatrix},\quad f_2 = \frac{i}{\sqrt{2}}\begin{pmatrix}0&{}\quad -1&{}\quad 0\\ 1&{}\quad 0&{}\quad -1\\ 0&{}\quad 1&{}\quad 0 \end{pmatrix},\quad f_3 = \begin{pmatrix}1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -1 \end{pmatrix} \end{aligned}$$

(A.10)

In closing, we also point out that the above relations are purely local symmetries, and are therefore completely independent of the boundary conditions satisfied by Q(x, t) as $x\rightarrow \pm \infty$.

1.2 A.2 Asymptotics of two-soliton interactions

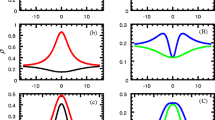
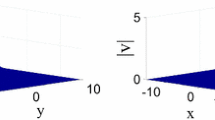
In this appendix we present a collection of figures to corroborate the asymptotics analysis of the two-soliton solutions discussed in Sect. 4. Figures 11, 12 and 13 display the difference between the exact two-soliton solution obtained from (51) with $J=2$ and the asymptotic expressions, presented in Sect. 4, computed along the direction of soliton 1 as $t\rightarrow -\infty$ (top row of each figure) and as $t\rightarrow \infty$ (bottom row). Specifically, Fig. 11 shows the case of a polar–polar two-soliton interaction, Fig. 12 that of a ferromagnetic–ferromagnetic soliton interaction, and Fig. 13 that of a polar–ferromagnetic interaction. For completeness, Fig. 14 also shows the same polar–ferromagnetic interaction but where the asymptotic behavior being subtracted is along the direction of soliton 2, since in this case the two solitons are of different type. The fact that the soliton leg vanishes in the appropriate limit in each case serves as a clear visual demonstration of the fact that the asymptotic expressions do indeed capture the correct behavior of the soliton in both of these limits, including both the redistribution of mass among the three spin components as well as the position and phase shift.

Fig. 11

Plot of the difference between a polar–polar two-soliton solution and its asymptotic expression along the direction of soliton 1, presented in Sect. 4.2. Top row: $t\rightarrow -\infty$. Bottom row: $t\rightarrow \infty$. The soliton parameters are the same as in Fig. 8

Fig. 12

Same as Fig. 11, but for a ferromagnetic–ferromagnetic two-soliton solution, whose asymptotics was presented in Sect. 4.3. The soliton parameters are as in Fig. 9

Fig. 13

Same as Fig. 11, but for a polar–ferromagnetic two-soliton solution, whose asymptotics was presented in Sect. 4.4. The soliton parameters are as in Fig. 10

Fig. 14

Same as Fig. 13, except that the asymptotic is now calculated along the direction of the ferromagnetic soliton. The soliton parameters are as in Fig. 10