Skip to main content
SpringerLink
Log in

Comparative study of the dynamics of entanglement and purity in two hybrid quantum systems under the effect of static noise

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

A comparative study of the dynamics of entanglement and purity in two hybrid quantum systems under the effect of a static noise is presented. The first system contains two qubits and one qutrit, while the second system contains one qubit and two qutrits. In addition, each system presents three configurations: the different, the common and the bipartite environment. In the bipartite environment, we have three cases depending on whether two subsystems are in the same environment and one subsystem in its environment alone. We found that in all these configurations, the same behavior is observed for negativity, purities and degrees of purity. The lower the purity, the more the degree of purity becomes and the system is less influenced by environmental corruption. Purity decreases more in the second system than in the first system and we can conclude that the second system preserves quantum properties better than the first.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. M. Born, P. Jordan, Zur Quantenmechanik. Z. Phys. 34, 858–888 (1925). https://doi.org/10.1007/BF01328531

    Article  ADS  MATH  Google Scholar 

  2. W. Bechtel, Using computational models to discover and understand mechanisms. Stud. Hist. Philos. Sci. Part A 56, 113–121 (2016)

    Article  Google Scholar 

  3. A. Einstein, B. Podolsky, N. Rosen, can quantum mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935)

    Article  ADS  Google Scholar 

  4. M. A. Nielsen, I. Chuang, Quantum computation and quantum information. 558–559 (2002)

  5. C.H. Bennett, S.J. Wiesner, Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69(20), 2881 (1992)

    Article  ADS  MathSciNet  Google Scholar 

  6. P.W. Shor, Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41(2), 303–332 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  7. L.T. Kenfack et al., Decoherence and tripartite entanglement dynamics in the presence of Gaussian and non-Gaussian classical noise. Phys. B Condens. Matter 511, 123–133 (2017)

    Article  ADS  Google Scholar 

  8. F. Buscemi, P. Bordone, Time evolution of tripartite quantum discord and entanglement under local and nonlocal random telegraph noise. Phys. Rev. A 87(4), 042310 (2013)

    Article  ADS  Google Scholar 

  9. L. Amico et al., Entanglement in many-body systems. Rev. Modern Phys. 80(2), 517 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  10. M. Li, S.-M. Fei, X. Li-Jost, Quantum entanglement: separability, measure, fidelity of teleportation, and distillation. Adv. Math. Phys. 2010 (2010)

  11. C.H. Bennett et al., Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70(13), 1895 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  12. S. Albeverio, S.-M. Fei, Teleportation of general finite-dimensional quantum systems. Phys. Lett. A 276(1–4), 8–11 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  13. Y. Yang, G. Chiribella, Is global asymptotic cloning state estimation?. arXiv preprint arXiv:1306.6427 (2013)

  14. M. Horodecki, P. Horodecki, R. Horodecki, General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 60(3), 1888 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  15. S. Albeverio, S.-M. Fei, W.L. Yang, Optimal teleportation based on bell measurements. Phys. Rev. A 66(1), 012301 (2002)

    Article  ADS  Google Scholar 

  16. A.K. Ekert, Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67(6), 661 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  17. D. Deutsch et al., Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77(13), 2818 (1996)

    Article  ADS  Google Scholar 

  18. C.A. Fuchs et al., Optimal eavesdropping in quantum cryptography. I. Information bound and optimal strategy. Phys. Rev. A 56(2), 1163 (1997)

    Article  ADS  MathSciNet  Google Scholar 

  19. K. Bakke, C. Furtado, Holonomic Quantum Computation with the Aharonov-Casher setup associated with topological defects. Quantum Inf. Comput. 11(5), 444–455 (2011)

    MathSciNet  MATH  Google Scholar 

  20. M. Zukowski et al., Event-ready-detectors Bell experiment via entanglement swapping. Phys. Rev. Lett. 71(26), 4287 (1993)

    Article  ADS  Google Scholar 

  21. S. Bose, V. Vedral, P.L. Knight, Multiparticle generalization of ntanglement swapping. Phys. Rev. A 57(2), 822 (1998)

    Article  ADS  Google Scholar 

  22. S. Bose, V. Vedral, P.L. Knight, Purification via entanglement swapping and conserved entanglement. Phys. Rev. A 60(1), 194 (1999)

    Article  ADS  Google Scholar 

  23. B.-S. Shi, Y.-K. Jiang, G.-C. Guo, Optimal entanglement purification via entanglement swapping. Phys. Rev. A 62(5), 054301 (2000)

    Article  ADS  Google Scholar 

  24. L. Hardy, D.D. Song, Entanglement-swapping chains for general pure states. Phys. Rev. A 62(5), 052315 (2000)

    Article  ADS  Google Scholar 

  25. C. Benedetti et al., Effects of classical environmental noise on entanglement and quantum discord dynamics. Int. J. Quantum Inf. 10(08), 1241005 (2012)

    Article  MathSciNet  Google Scholar 

  26. R. Lo Franco et al., Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Modern Phys. B 27, 1345053 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  27. A. Serafini et al., Entanglement and purity of two-mode Gaussian states in noisy channels. Phys. Rev. A 69(2), 022318 (2004)

    Article  ADS  Google Scholar 

  28. G. Vidal et al., Computable mesure of entanglement. Phys. Rev. A 65(3), 032314 (2002)

    Article  ADS  Google Scholar 

  29. A. Peres, Separability criterion for density matrices. Phys. Rev. Lett. 77(8), 1413 (1996)

    Article  ADS  MathSciNet  Google Scholar 

  30. G. Waldherr et al., Quantum error correction in a solid-state hybrid spin register. Nature 506(7487), 204 (2014)

    Article  ADS  Google Scholar 

  31. M. Tchoffo et al., Frozen entanglement and quantum correlations of one-parameter qubit− qutrit states under classical noise effects. Phys. Lett. A 383(16), 1856–1864 (2019)

    Article  ADS  Google Scholar 

  32. T.K. Lionel et al., Effects of static noise on the dynamics of quantum correlations for a system of three qubits. Int. J. Modern Phys. B 31(8), 1750046 (2017)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Unité de Recherche de Matière Condensée, d´Electronique Et de Traitement du Signal (URMACETS), Department of Physics, Dschang School of Sciences and Technology, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Lionel Tenemeza Kenfack, Martin Tchoffo & Lukong Cornelius Fai

  2. Department of Physics, Faculty of Science, University of Maroua, P.O. Box 814, Maroua, Cameroon

    Odette Melachio Tiokang, Fridolin Nya Tchangnwa & Jaures Diffo Tchinda

  3. Faculté D’agronomie Et Des Sciences Agricoles, Centre d’Etudes Et de Recherches en Agronomie Et en Biodiversité (CERAB), University of Dschang, P.O. 222, Dschang, Cameroon

    Martin Tchoffo

Authors
  1. Odette Melachio Tiokang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fridolin Nya Tchangnwa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jaures Diffo Tchinda
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lionel Tenemeza Kenfack
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Martin Tchoffo
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Lukong Cornelius Fai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin Tchoffo.

Appendices

Appendix A Explicit derivation of the density matrix of the two systems in the different environment, common and bipartite environments

  1. A

    First system: two qubits and one qutrit

  1. (A1)

    Independent environments (de)

For the case of local coupling to different environments the density matrix \(\rho_{1de} (t),\) of the system at time t, reads:

$$ \rho_{1de} (t) = \left( {\begin{array}{*{20}c} {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{121d}^{ + } } \\ 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{112d}^{ + } } & 0 \\ 0 & 0 & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{103d}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & {\rho_{94d}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & {\rho_{85d}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & {\rho_{76d}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{76d} } & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{85d} } & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{94d} } & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{103d} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & 0 & 0 \\ 0 & {\rho_{112d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 \\ {\rho_{121d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } \\ \end{array} } \right) $$
$$ \rho_{11d} = \frac{p}{4};k3\rho_{33d} = \frac{1}{4}\left( {1 - 2p} \right); $$
$$ \begin{aligned} \rho_{121d} = & \frac{p}{{4\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} + c_{0} J_{2} + c_{0} J_{3} } \right)t} \right\} \\ & \quad \sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) \\ \end{aligned} $$
$$ \rho_{112d} = \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} J_{1} J_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J_{1} + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \begin{aligned} \rho_{103d} =\, & \frac{{\left( {1 - 2p} \right)}}{{4\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} + c_{0} J_{2} - c_{0} J_{3} } \right)t} \right\} \\ & \quad \sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) \\ \end{aligned} $$
$$ \begin{aligned} \rho_{94d} =\, & \frac{p}{{4\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} - c_{0} J_{2} + c_{0} J_{3} } \right)t} \right\} \\ & \quad \sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) \\ \end{aligned} $$
$$ \rho_{85d} =\, \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} J_{1} J_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J_{1} - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \begin{aligned} \rho_{76d} =\, & \frac{{\left( {1 - 2p} \right)}}{{4\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} - c_{0} J_{2} - c_{0} J_{3} } \right)t} \right\} \\ & \quad \sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) \\ \end{aligned} $$
  1. (A2)

    Common environment (Ce)

$$ \rho_{1ce} (t) = \left( {\begin{array}{*{20}c} {\rho_{11c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{121c}^{ + } } \\ 0 & {\rho_{11c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{112c}^{ + } } & 0 \\ 0 & 0 & {\rho_{33c} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{103c}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11c} } & 0 & 0 & 0 & 0 & {\rho_{94c}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11c} } & 0 & 0 & {\rho_{85c}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33c} } & {\rho_{76c}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{76c} } & {\rho_{33c} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{85c} } & 0 & 0 & {\rho_{11c} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{94c} } & 0 & 0 & 0 & 0 & {\rho_{11c} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{103c} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33c} } & 0 & 0 \\ 0 & {\rho_{112c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11c} } & 0 \\ {\rho_{121c} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11c} } \\ \end{array} } \right) $$

With:

$$ \rho_{11c} = \frac{p}{4};\quad \rho_{33c} = \frac{1}{4}\left( {1 - 2p} \right) $$
$$ \rho_{121c} = \frac{p}{{\left( {12J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 3Jc_{0} } \right)t} \right\}\sin \left( {3Jt\Delta_{c} } \right) $$
$$ \rho_{112c} = \frac{p}{{\left( {8J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + 2Jc_{0} } \right)t} \right\}\sin \left( {2Jt\Delta_{c} } \right) $$
$$ \rho_{103c} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
$$ \rho_{94c} = \frac{p}{{\left( {4J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
$$ \rho_{85c} = \frac{p}{4}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} } \right)t} \right\} $$
$$ \rho_{76c} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
  1. (A3)

    Bipartite environments coupling (be)

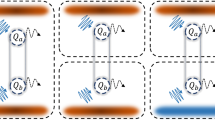
In the case of bipartite environments, two subsystems interact with a common environment. We have envisaged three possibilities:

  1. a—

    The case where \(\left( {Q_{1} } \right)\) and \(\left( {Q_{2} } \right)\) are in common environment.

$$ \rho_{1Bea} (t) = \left( {\begin{array}{*{20}c} {\rho_{11Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{121Ba}^{ + } } \\ 0 & {\rho_{11Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{112Ba}^{ + } } & 0 \\ 0 & 0 & {\rho_{33Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{103Ba}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11Ba} } & 0 & 0 & 0 & 0 & {\rho_{94Ba}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11Ba} } & 0 & 0 & {\rho_{85Ba}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33Ba} } & {\rho_{76Ba}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{76Ba} } & {\rho_{33Ba} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{85Ba} } & 0 & 0 & {\rho_{11Ba} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{94Ba} } & 0 & 0 & 0 & 0 & {\rho_{11Ba} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{103Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33Ba} } & 0 & 0 \\ 0 & {\rho_{112Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Ba} } & 0 \\ {\rho_{121Ba} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Ba} } \\ \end{array} } \right) $$

With:

$$ \rho_{11Ba} = \frac{p}{4};\quad \rho_{33Ba} = \frac{1}{4}\left( {1 - 2p} \right) $$
$$ \rho_{121Ba} = \frac{p}{{8\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J + c_{0} J_{3} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{112Ba} = \frac{p}{{\left( {8\Delta_{c} Jt} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + 2c_{0} J} \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right) $$
$$ \rho_{103Ba} = \frac{{\left( {1 - 2p} \right)}}{{8\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + 2c_{0} J - c_{0} J_{3} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{94Ba} = \frac{p}{{\left( {4\Delta_{c} tJ_{3} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{85Ba} = \frac{p}{4}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} } \right)t} \right\} $$
$$ \rho_{76Ba} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4\Delta_{c} tJ_{3} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{3} } \right) $$
  1. b—

    The case where \(\left( {Q_{1} } \right)\) and \(\left( {Q_{3} } \right)\) are in common environment.

$$ \rho_{1Beb} (t) = \left( {\begin{array}{*{20}c} {\rho_{11Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{121Bb}^{ + } } \\ 0 & {\rho_{11Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{112Bb}^{ + } } & 0 \\ 0 & 0 & {\rho_{33Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{103Bb}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11Bb} } & 0 & 0 & 0 & 0 & {\rho_{94Bb}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11Bb} } & 0 & 0 & {\rho_{85Bb}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33Bb} } & {\rho_{76Bb}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{76Bb} } & {\rho_{33Bb} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{85Bb} } & 0 & 0 & {\rho_{11Bb} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{94Bb} } & 0 & 0 & 0 & 0 & {\rho_{11Bb} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{103Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33Bb} } & 0 & 0 \\ 0 & {\rho_{112Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Bb} } & 0 \\ {\rho_{121Bb} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Bb} } \\ \end{array} } \right) $$

With:

$$ \rho_{11Bb} = \frac{p}{4};\quad \rho_{33Bb} = \frac{1}{4}\left( {1 - 2p} \right) $$
$$ \rho_{121Bb} = \frac{p}{{8\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J + c_{0} J_{2} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{112Bb} = \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{103Bb} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4\Delta_{c} tJ_{2} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{94Bb} = \frac{p}{{8\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J - c_{0} J_{2} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{85Bb} = \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{76Bb} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4\Delta_{c} tJ_{2} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{2} } \right) $$
  1. c—

    The case where \(\left( {Q_{2} } \right)\) and \(\left( {Q_{3} } \right)\) are in common environment.

$$ \rho_{1Bec} (t) = \left( {\begin{array}{*{20}c} {\rho_{11Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{121Bc}^{ + } } \\ 0 & {\rho_{11Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{112Bc}^{ + } } & 0 \\ 0 & 0 & {\rho_{33Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{103Bc}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11Bc} } & 0 & 0 & 0 & 0 & {\rho_{94Bc}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11Bc} } & 0 & 0 & {\rho_{85Bc}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33Bc} } & {\rho_{76Bc}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{76Bc} } & {\rho_{33Bc} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{85Bc} } & 0 & 0 & {\rho_{11Bc} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{94Bc} } & 0 & 0 & 0 & 0 & {\rho_{11Bc} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{103Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33Bc} } & 0 & 0 \\ 0 & {\rho_{112Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Bc} } & 0 \\ {\rho_{121Bc} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11Bc} } \\ \end{array} } \right) $$

With:

$$ \rho_{11Bc} = \frac{p}{4};\quad \rho_{33Bc} = \frac{1}{4}\left( {1 - 2p} \right) $$
$$ \rho_{121Bc} = \frac{p}{{8\left( {\Delta_{c} t} \right)^{2} JJ_{1} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} + 2c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {2\Delta_{c} tJ} \right) $$
$$ \rho_{112Bc} = \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J_{1} + c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
$$ \rho_{103Bc} = \frac{{\left( {1 - 2p} \right)}}{{\left( {4\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
$$ \rho_{94Bc} = \frac{p}{{\left( {4\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
$$ \rho_{85Bc} = \frac{p}{{4\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J_{1} - c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
$$ \rho_{76Bc} = \frac{{\left( {1 - 2p} \right)}}{{8\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} - 2c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {2\Delta_{c} tJ} \right) $$
  1. B—

    Second system: one qubit and two qutrits

  1. (B1)

    independent environments (de)

$$ \rho_{2de} (t) = \left( {\begin{array}{*{20}c} {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{181d}^{ + } } \\ 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{172d}^{ + } } & 0 \\ 0 & 0 & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{163d}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{154d}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{145d}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{136d}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & {\rho_{127d}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & {\rho_{118d}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & {\rho_{109d}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{109d} } & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{118d} } & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{127d} } & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{136d} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{145d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{154d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{163d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33d} } & 0 & 0 \\ 0 & {\rho_{172d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } & 0 \\ {\rho_{181d} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11d} } \\ \end{array} } \right) $$
$$ \rho_{11d} = \frac{p}{6};\quad \rho_{33d} = \frac{1}{6}\left( {1 - 2p} \right) $$
$$ \rho_{181d} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} + c_{0} J_{2} + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{172d} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J_{1} + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
$$ \rho_{163d} = \frac{{\left( {1 - 2p} \right)}}{{6\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} + c_{0} J_{2} - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{154d} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{3} + c_{0} J_{1} + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{145d} = \frac{p}{{\left( {6\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
$$ \rho_{136d} = \frac{1 - 2p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{3} + c_{0} J_{1} - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{127d} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} - c_{0} J_{2} + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{118d} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J_{1} - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$

\(\rho_{109d} = \frac{{\left( {1 - 2p} \right)}}{{6\left( {\Delta_{c} t} \right)^{3} J_{1} J_{2} J_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} - c_{0} J_{2} - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ_{2} } \right)\sin \left( {\Delta_{c} tJ_{3} } \right)\)

  1. (B2)

    Common environments (ce)

$$ \rho_{11c} = \frac{p}{6};\quad \rho_{33c} = \frac{1}{6}\left( {1 - 2p} \right) $$
$$ \rho_{181c} = \frac{p}{{\left( {18J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 3Jc_{0} } \right)t} \right\}\sin \left( {3Jt\Delta_{c} } \right) $$
$$ \rho_{172c} = \frac{p}{{\left( {12J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + 2Jc_{0} } \right)t} \right\}\sin \left( {2Jt\Delta_{c} } \right) $$
$$ \rho_{163c} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
$$ \rho_{154c} = \frac{p}{{\left( {12J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{3} + 2Jc_{0} } \right)t} \right\}\sin \left( {2Jt\Delta_{c} } \right) $$
$$ \rho_{145c} = \frac{p}{{\left( {6J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
$$ \rho_{136c} = \frac{1 - 2p}{6}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{3} } \right)t} \right\} $$
$$ \rho_{127c} = \frac{p}{{\left( {6J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
$$ \rho_{118c} = \frac{p}{6}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} } \right)t} \right\} $$
$$ \rho_{109c} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6J\Delta_{c} t} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - Jc_{0} } \right)t} \right\}\sin \left( {Jt\Delta_{c} } \right) $$
  1. (B3)

    Bipartite environments (be)

  1. a—

    The case where \(\left( {Q_{1} } \right)\) and \(\left( {Q_{2} } \right)\) are in common environment.

$$ \rho_{11Bea} = \frac{p}{6};\quad \rho_{33Bea} = \frac{1}{6}\left( {1 - 2p} \right) $$
$$ \rho_{181Bea} = \frac{p}{{12\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J + c_{0} J_{3} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{172Bea} = \frac{p}{{\left( {12\Delta_{c} Jt} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + 2c_{0} J} \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right) $$
$$ \rho_{163Ba} = \frac{{\left( {1 - 2p} \right)}}{{12\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + 2c_{0} J - c_{0} J_{3} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{154Bea} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{3} + c_{0} J + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{145Bea} = \frac{p}{{\left( {6\Delta_{c} tJ} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right) $$
$$ \rho_{136Bea} = \frac{{\left( {1 - 2p} \right)}}{{6\left( {\Delta_{c} t} \right)^{2} JJ_{3} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{3} + c_{0} J - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{127Bea} = \frac{p}{{\left( {6\Delta_{c} tJ_{3} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{3} } \right) $$
$$ \rho_{118Bea} = \frac{p}{6}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} } \right)t} \right\} $$
$$ \rho_{109Bea} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6\Delta_{c} tJ_{3} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - c_{0} J_{3} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{3} } \right) $$
  1. b—

    The case where \(\left( {Q_{1} } \right)\) and \(\left( {Q_{3} } \right)\) are in common environment.

    $$ \rho_{11Beb} = \frac{p}{6};\quad \rho_{33Beb} = \frac{1}{6}\left( {1 - 2p} \right) $$
    $$ \rho_{181Beb} = \frac{p}{{12\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J + c_{0} J_{2} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
    $$ \rho_{172Beb} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
    $$ \rho_{163Beb} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6\Delta_{c} tJ_{2} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{2} } \right) $$
    $$ \rho_{154Beb} = \frac{p}{{\left( {12\Delta_{c} tJ} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{3} + 2c_{0} J} \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right) $$
    $$ \rho_{145Beb} = \frac{p}{{\left( {6\Delta_{c} tJ} \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right) $$
    $$ \rho_{136Beb} = \frac{1 - 2p}{6}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{3} } \right)t} \right\} $$
    $$ \rho_{127Beb} = \frac{p}{{12\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + 2c_{0} J - c_{0} J_{2} } \right)t} \right\}\sin \left( {2\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
    $$ \rho_{118Beb} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} JJ_{2} }}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ} \right)\sin \left( {\Delta_{c} tJ_{2} } \right) $$
    $$ \rho_{109Beb} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6\Delta_{c} tJ_{2} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} - c_{0} J_{2} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{2} } \right) $$
  1. c—

    The case where \(\left( {Q_{2} } \right)\) and \(\left( {Q_{3} } \right)\) are in common environment.

    $$ \rho_{11Bec} = \frac{p}{6};\quad \rho_{33Bec} = \frac{1}{6}\left( {1 - 2p} \right) $$
    $$ \rho_{181Bec} = \frac{p}{{12\left( {\Delta_{c} t} \right)^{2} JJ_{1} }}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} + 2c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {2\Delta_{c} tJ} \right) $$
    $$ \rho_{172Bec} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} + c_{0} J_{1} + c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
    $$ \rho_{163Bec} = \frac{{\left( {1 - 2p} \right)}}{{\left( {6\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
    $$ \rho_{154Bec} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} + \varepsilon_{3} + c_{0} J_{1} + c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
    $$ \rho_{145Bec} = \frac{p}{{\left( {6\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
    $$ \rho_{136Bec} = \frac{1 - 2p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{3} + c_{0} J_{1} - c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
    $$ \rho_{127Bec} = \frac{p}{{\left( {6\Delta_{c} tJ_{1} } \right)}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + \varepsilon_{3} + c_{0} J_{1} } \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right) $$
    $$ \rho_{118Bec} = \frac{p}{{6\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} + c_{0} J_{1} - c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {\Delta_{c} tJ} \right) $$
    $$ \rho_{109Bec} = \frac{{\left( {1 - 2p} \right)}}{{12\left( {\Delta_{c} t} \right)^{2} J_{1} J}}\exp \left\{ {2i\left( {\varepsilon_{1} - \varepsilon_{2} - \varepsilon_{3} + c_{0} J_{1} - 2c_{0} J} \right)t} \right\}\sin \left( {\Delta_{c} tJ_{1} } \right)\sin \left( {2\Delta_{c} tJ} \right) $$

Appendix B Explicit derivation of the partial transposed of these matrices

  • First system

The transpose with respect to \(Q_{1}\) is equal to The transpose with respect to \(Q_{3}\).

$$ \rho_{1Q1} = \rho_{1}^{T1} = \left( {\begin{array}{*{20}c} {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{76} } \\ 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{85} } & 0 \\ 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{94} } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & {\rho_{103} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & {\rho_{112} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & {\rho_{121} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{121}^{ + } } & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{112}^{ + } } & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{103}^{ + } } & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{94}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 \\ 0 & {\rho_{85}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 \\ {\rho_{76}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } \\ \end{array} } \right) $$

The transpose with respect to the second Qubit is:

$$ \rho_{1Q2} = \rho_{1}^{T2} = \left( {\begin{array}{*{20}c} {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{94}^{ + } } \\ 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{85}^{ + } } & 0 \\ 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{76}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & {\rho_{121}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & {\rho_{112}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & {\rho_{103}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{103} } & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{112} } & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{121} } & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{76} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 \\ 0 & {\rho_{85} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 \\ {\rho_{94} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } \\ \end{array} } \right) $$

  • Second system

$$ \rho_{2Q1} = \rho_{2}^{T1} = \rho_{2Q3} = \left( {\begin{array}{*{20}c} {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{109} } \\ 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{118} } & 0 \\ 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{127} } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{136} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{145} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{154} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & {\rho_{163} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & {\rho_{172} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & {\rho_{181} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{181}^{ + } } & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{172}^{ + } } & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{163}^{ + } } & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{154}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{145}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{136}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{127}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 \\ 0 & {\rho_{118}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 \\ {\rho_{109}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } \\ \end{array} } \right) $$
$$ \rho_{2Q2} = \rho_{2}^{T2} = \left( {\begin{array}{*{20}c} {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{127}^{ + } } \\ 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{118}^{ + } } & 0 \\ 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{109}^{ + } } & 0 & 0 \\ 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{154}^{ + } } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{145}^{ + } } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{136}^{ + } } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & {\rho_{181}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & {\rho_{172}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & {\rho_{163}^{ + } } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{163} } & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{172} } & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{181} } & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho_{136} } & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho_{145} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho_{154} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 & 0 & 0 \\ 0 & 0 & {\rho_{109} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{33} } & 0 & 0 \\ 0 & {\rho_{118} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } & 0 \\ {\rho_{127} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\rho_{11} } \\ \end{array} } \right) $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tiokang, O.M., Tchangnwa, F.N., Tchinda, J.D. et al. Comparative study of the dynamics of entanglement and purity in two hybrid quantum systems under the effect of static noise. Eur. Phys. J. Plus 136, 957 (2021). https://doi.org/10.1140/epjp/s13360-021-01950-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01950-7

Search

Navigation