Skip to main content
SpringerLink
Log in

Weakly nonlinear thermohaline convection in a sparsely packed porous medium due to horizontal magnetic field

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

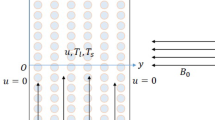
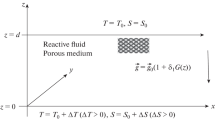
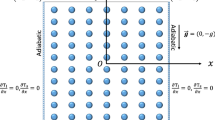
Thermohaline convection in a sparsely packed porous medium is studied due to horizontal magnetic field, using both linear and weakly nonlinear stability analyses. The Darcy–Lapwood–Brinkman (DLB) model is employed as the momentum equation. In the linear stability analysis, the normal mode technique is used to find the thermal critical Rayleigh number which is a function of q, Da, \(\Lambda \), \(R_2\) and L. In the weakly nonlinear analysis, a nonlinear two-dimensional Landau–Ginzburg (LG) equation is derived at the onset of stationary convection and the secondary instabilities and heat transport by convection are studied. Coupled one-dimensional LG equations are derived at the onset of oscillatory convection, and the stability regions of steady state, standing waves and travelling waves are studied.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Availability Statement

This manuscript has associated data in a data repository. [Authors’ comment: The data used to support the findings of this study are included within the article (https://doi.org/10.1615/JPorMedia.v10.i8.70)].

Abbreviations

\(\overline{V}\) :

Vector fluid velocity

u,  v,  w :

Velocity components

\(\overline{H}\) :

Vector magnetic field

\(H_x,H_y,H_z\) :

Magnetic field components

\(\Delta T\) :

Temperature difference

\(\Delta S\) :

Salinity difference

P :

Pressure

g :

Acceleration due gravity

\(k_T\) :

Thermal diffusivity

\(k_S\) :

Saline diffusivity

k :

Permeability

\(A_{1L}\) :

Amplitude of left travelling waves

\(A_{1R}\) :

Amplitude of right travelling waves

A :

Complex amplitude

Da :

Darcy number

L :

Lewis number

\(\Lambda \) :

Brinkman number

M :

Non-dimensional heat capacity

Nu :

Nusselt number

\(Pr_1\) :

Thermal Prandtl number

\(Pr_2\) :

Magnetic Prandtl number

q :

Wavenumber

Q :

Chandrasekhar number

\(R_1\) :

Thermal Rayleigh number

\(R_2\) :

Magnetic Rayleigh number

\(\alpha \) :

Thermal expansion coefficient

\(\beta \) :

Solute expansion coefficient

\(\eta \) :

Magnetic diffusivity

\(\mu \) :

Fluid viscosity

\(\mu _e\) :

Effective fluid viscosity

\(\mu _m \) :

Magnetic permeability

\(\phi \) :

Porosity

\(\rho \) :

Fluid density

\(\nu \) :

Kinematic viscosity

\(\omega \) :

Vorticity

References

  1. D.A. Nield, Onset of thermohaline convection in a porous medium. Water Resour. Res. 4, 553–560 (1968)

    Article  ADS  Google Scholar 

  2. N. Rudraiah, P.K. Srimani, R. Friedrich, Finite amplitude convection in a two component fluid saturated porous layer. Int. J. Heat Mass Transf. 25, 715–722 (1982)

    Article  Google Scholar 

  3. B.S. Bhadauria, Double diffusive convection in a porous medium with modulated temperature on the boundaries. Transp. Porous Media 70, 191–211 (2007)

    Article  MathSciNet  Google Scholar 

  4. M.S. Malashetty, M. Swamy, R. Heera, Double diffusive convection in a porous layer using a thermal non-equilibrium model. Int. J. Thermal Sci. 47(9), 1131–1147 (2008)

    Article  Google Scholar 

  5. M.S. Malashetty, I. Pop, R. Heera, Linear and nonlinear double diffusive convection in a rotating sparsely packed porous layer using a thermal non-equilibrium model. Continuum Mech. Thermodyn. 21, 317–339 (2009)

    Article  ADS  MathSciNet  Google Scholar 

  6. P. Kumar, Thermosolutalmagnetorotatory convection in couple stress fluid through porous medium. J. App. Fluid Mechanics 5, 45–52 (2012)

    Google Scholar 

  7. D.A. Nield, A. Bejan, Convection in a Porous Media, 3rd edn. (Springer Verlag, Berlin, 2006)

    MATH  Google Scholar 

  8. E.R. Lapwood, Convection of a fluid in a porous medium. Proc Camb Phil Soc 44, 508–521 (1948)

    Article  ADS  MathSciNet  Google Scholar 

  9. A. Benerji Babu, R. Ravi, S.G. Tagare, Nonlinear rotating convection in a sparsely packed porous medium. Commun. Nonlinear Sci. Numer. Simul. 17(12), 5042–5063 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  10. W.B. Thompson, Thermal convection in a magnetic field. Phil. Mag. 42(335), 1417–1432 (1951)

    Article  MathSciNet  Google Scholar 

  11. S. Chandrasekhar, Hydrodynamic and Hydromagnetic Stability (Clarendon Press, Oxford, 1961)

    MATH  Google Scholar 

  12. P.G. Drazin, W.H. Reid, Hydrodynamic Stability (Cambridge University Press, London, 2004)

    Book  Google Scholar 

  13. S.A. Balbus, J.F. Hawley, A powerful local shear instability in weakly magnetized disks. IV. Nonaxisymmetric perturbations. Astrophys. J. 400, 610–621 (1992)

    Article  ADS  Google Scholar 

  14. V. Steinberg, H.R. Brand, Crossover from critical to tricritical behavior in a nonequilibrium system: the convective instability in a binary fluid mixture. Phys. Rev. 30A, 3366–3368 (1984)

    Article  ADS  Google Scholar 

  15. S.G. Tagare, A. Benerji Babu, Nonlinear convection in a Sparsely packed porous medium due to compositional and thermal buoyancy. J. Porous Medium 10, 823–839 (2007)

    Article  Google Scholar 

  16. S.G. Tagare, A. Benerji Babu, Y. Rameshwar, Rayleigh Benard convection in rotating fluids. Int. J. Heat Mass Transf. 51(5), 1168–1178 (2008)

    Article  Google Scholar 

  17. A. Benerji Babu, B. Shanker, S.G. Tagare, Non-linear convection due to compositional and thermal buoyancy in Earths outer core. Int. J. Non-linear Mech. 46, 919–930 (2011)

    Article  ADS  Google Scholar 

  18. A. Benerji Babu, R. Ragoju Ravi, S.G. Tagare, Nonlinear thermohaline magnetoconvection in a sparcely packed porous medium. J. Porous Media 17(1), 31–57 (2014)

    Article  Google Scholar 

  19. A.C. Newell, J.A. Whitehead, Finite bandwidth, finite amplitude convection. J. Fluid Mech. 38, 279–303 (1969)

    Article  ADS  MathSciNet  Google Scholar 

  20. E. Knobloch, J. De Luca, Amplitude equations for travelling wave convection. Nonlinearty 3, 975–980 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  21. P. Coullet, S. Fauve, E. Tirapegui, Large scale instability of non-linear standing waves. J. de Phys. Lett. 46, 787–791 (1985)

    Article  Google Scholar 

  22. P.C. Matthews, A.M. Rucklidge, Travelling and standing waves in magnetoconvection. Proc. R. Soc. Lond. A 441, 649–658 (1993)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Warangal, Warangal, 506004, India

    A. Benerji Babu & S. G. Tagare

  2. Department of HBS, Godavari Institute of Engineering and Technology, Rajahmundry, Andhra Pradesh, 533296, India

    N. Venkata Koteswara Rao

Authors
  1. A. Benerji Babu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Venkata Koteswara Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. G. Tagare
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Benerji Babu.

Appendix

Appendix

In linear stability analysis, the thermal Rayleigh number \(R_1\) coefficients are

$$\begin{aligned} \mathcal{K}&=\left( \delta ^4 +\frac{\phi ^2}{L^2}\omega ^2\right) ^{-1}\left( M^2 \delta ^4 +\phi ^2 \frac{Pr_2^2}{Pr_1^2}\omega ^2\right) ^{-1}, \nonumber \\ c_0&=M \delta ^8\left( Q m^2 \delta ^2+\frac{1}{Da}+\Lambda \delta ^6 +\frac{R_2}{L}q^2\right) ,\nonumber \\ c_1&=\Big [M(m^2 Q \delta ^2 + \frac{\delta ^4}{Da}+\Lambda \delta ^6)+\frac{\delta ^6}{Pr_1}\left( \frac{1}{\phi }-m^2 Q\phi Pr_2 \delta ^2\right) +\frac{M q^2 R_2}{L^2}(L-\phi )\Big ]\delta ^6,\nonumber \\ c_2&= \frac{\delta ^{10}}{\phi Pr_1}-\frac{q^2 \delta ^4 \phi R_2}{L}\left( \frac{M}{L}+\frac{\phi }{M}\frac{Pr_2^2}{Pr_1^2}\right) -\delta ^8 \phi ^2 M \left( \frac{1}{L^2}+\frac{1}{M^2}\frac{Pr_2^2}{Pr_1^2}\right) \left( \frac{1}{Da}+\delta ^2 \Lambda \right) \nonumber \\&\quad - m^2 Q \delta ^6 \phi (\frac{M\phi }{L^2}+\frac{Pr_2}{Pr_1}), \nonumber \\ c_3&=\frac{q^2 \delta ^2 \phi ^2}{L^2 M}\frac{Pr_2^2}{Pr_1^2}R_2 (\phi -L)-\Big [ M \delta ^6 \phi ^2 \left( \frac{1}{Da}+\delta ^2 \Lambda \right) -\frac{\phi \delta ^8}{Pr_1}\Big ]\left( \frac{1}{M^2}\frac{Pr_2^2}{Pr_1^2}+\frac{1}{L^2}\right) \nonumber \\&\quad -\frac{m^2 Q\delta ^4 \phi ^2}{L^2}(M-\phi \frac{Pr_2}{Pr_1}), \nonumber \\ c_4=&\frac{\delta ^4 \phi ^4}{L^2 M}\frac{Pr_2^2}{Pr_1^2}\left( \frac{1}{Da}+\Lambda \delta ^2\right) +\frac{q^2 \phi ^3}{L^2M}\frac{Pr_2^2}{Pr_1^2} R_2-\frac{\delta ^6 \phi }{Pr_1}\left( \frac{1}{L^2}+\frac{1}{M^2}\frac{Pr_2^2}{Pr_1^2}\right) +\frac{m^2 Q\delta ^6 \phi ^3}{L^3}\frac{Pr_2}{Pr_1}, \nonumber \\ c_5&=\frac{\delta ^2 \phi ^4}{L^2 M}\frac{Pr_2^2}{Pr_1^2}\left( \frac{1}{Da}+\Lambda \delta ^2+\frac{\delta ^2}{M\phi Pr_1}\right) , \nonumber \\ c_6&=\frac{\delta ^2 \phi ^3 Pr_2^2}{L^2 M^2 Pr_1^3}. \end{aligned}$$
(66)

At marginal stability analysis, when \(R_1\) is an independent variable, the following are the coefficients of polynomial in p,

$$\begin{aligned} A&=\frac{\delta ^4 \phi Pr_2}{L M^2 Pr_1^2} ,\nonumber \\ B&= \frac{\delta ^4 Pr_2}{M^2 Pr_1^2}\left( 1+\frac{\phi }{L}\right) +\frac{\delta ^2 \phi ^2 Pr_2}{L M Pr_1}\left( \Lambda +\frac{1}{Da}\right) +\frac{\delta ^4}{L M Pr_1} ,\nonumber \\ C&=\frac{\phi \delta ^2}{L}\left( m^2 Q+\frac{\delta ^2}{Da}\right) +\frac{\delta ^4 \phi Pr_2}{M Pr_1}\left( 1+\frac{\phi }{L}\right) \left( \Lambda \phi \delta ^2 + \frac{1}{Da}\right) +\frac{\delta ^6}{M Pr_1}\left( \frac{1}{\phi }+\frac{Pr_2}{M Pr_1}\right) \nonumber \\&\quad +\frac{\delta ^6}{L}\left( \Lambda \phi +\frac{1}{MPr_1}\right) +\frac{q^2 \phi Pr_2}{L M Pr_1}(R_1 - R_1 \phi ) ,\nonumber \\ D&=q^2 \delta ^2 \left[ \frac{\phi Pr_2}{M Pr_1}\left( R_1 +\frac{R_2}{L}\right) +\frac{1}{L}(R_1 -\phi R_1) \right] +m^2 Q \delta ^4 \left( 1+\frac{\phi }{L}\right) +\frac{\delta 6}{Da}(1+\frac{\phi }{L} \nonumber \\&\quad +\frac{\phi Pr_2}{M Pr_1})+ \delta ^8 \left[ \Lambda \left( 1+\frac{\phi }{L}\right) +\frac{1}{MPr_1}\left( \Lambda \phi Pr_2 +\frac{1}{\phi }\right) \right] ,\nonumber \\ E&=\delta ^4 \left[ m^2 Q\delta ^2 +\delta ^4 (\Lambda \delta ^2 )+\frac{1}{Da}-q^2 \left( R_1-\frac{R_2}{L})\right) \right] . \end{aligned}$$
(67)

These are coefficients of coupled LG equation derived at the onset of oscillatory convection.

$$\begin{aligned} \Lambda _{0}&=\left[ \delta ^4 \left( 1+\frac{\phi }{L}\right) \left( m^2Q+\frac{\delta ^2}{Da}+\Lambda \delta ^2\right) -(\phi R_1-R_2)\frac{q^2 \delta ^2}{L}-\frac{q^2 \delta ^2 \phi R_{12}Pr_2}{M Pr_1} \right. \nonumber \\&\quad -\frac{3 \delta ^4 \omega ^2 Pr_2}{M^2 Pr_1^2}\left( 1+\frac{\phi }{L}\right) +\frac{\delta ^2 \phi Pr_2}{M Pr_1}(\frac{1}{+}{Da}+\Lambda \delta ^2)\left( \delta ^4-\frac{3 \phi ^2 \omega ^2}{L}\right) +\frac{\delta ^4}{M Pr_1}\nonumber \\&\quad \left( \frac{\delta ^4}{\phi }-\frac{3 \omega ^2}{L}\right) \Big ]+i \Big [\frac{2 \delta ^6 \omega }{L}\left( \Lambda \phi +\frac{1}{M Pr_1}\right) +\frac{2 \delta ^6 \omega }{M Pr_1}\left( \frac{1}{\phi }+\frac{Pr_2}{M Pr_1}\right) +\frac{2 \delta ^2 \phi \omega }{L}\nonumber \\&\quad \left( m^2Q+\frac{\delta ^2}{Da}\right) +\frac{2 \delta ^4 \phi \omega Pr_2}{M Pr_1}\left( \frac{1}{Da}+\Lambda \delta ^2\right) \left( 1+\frac{\phi }{L}\right) -\frac{4\delta ^2 \phi \omega ^3 Pr_2}{L M^2 Pr_1^2}\Big ], \nonumber \\ \Lambda _{1}&=\Big [\frac{q^2 \phi Pr_2}{L M Pr_1}(R_2 -\phi R_1)+\frac{\delta 6}{M Pr_1}\left( \frac{1}{L}+\frac{1}{\phi }+\frac{Pr_2}{Pr_1}\right) +\frac{\delta ^2 \phi }{L}\left( m^2 Q-\frac{6 \omega ^2Pr_2}{M^2 Pr_1^2}\right) \nonumber \\&\quad +\delta ^4 \phi \left( \frac{1}{Da}+\delta ^2 \Lambda \right) \left( \frac{1}{L}+\frac{Pr_2}{Pr_1}+\frac{\phi Pr_2}{L M Pr_1}\right) \Big ]+i \Big [\frac{3\delta ^2 \phi ^2 \omega Pr_2}{L M Pr_1}\left( \frac{1}{Da}+\delta ^2 \Lambda \right) \nonumber \\&\quad +\left. \frac{3\delta ^2 \omega }{M Pr_1}\left( \frac{1}{L}+\frac{Pr_2}{M Pr_1}+\frac{\phi Pr_2}{L M Pr_1}\right) \right] , \nonumber \\ \Lambda _2&=\Bigg [\frac{\delta ^2 \phi \omega ^2 Pr_2}{M Pr_1}\left( 1+\frac{\phi }{L}\right) \left( \frac{2}{Da}+3 \Lambda \delta ^2\right) + \frac{3 \delta ^4 \omega ^2}{M Pr_1}\left( \frac{1}{L}+\frac{1}{\phi }+\frac{Pr_2}{M Pr_1}\right) \nonumber \\&\quad -\left( \frac{\omega ^2}{M Pr_1}+\phi R_1 - R_2\right) +\delta ^2 \left( R_1 - \frac{R_2}{L}\right) (2 Qq^2 +\delta ^2)+\frac{\phi \omega ^2}{L}\left( m^2 Q+\frac{2\delta ^2}{Da}\right) \nonumber \\&\quad +\delta ^4\left( 3m^2Q+\frac{4 \delta ^2}{Da}+5 \Lambda \delta ^4-\frac{3 \omega ^2 \Lambda \delta ^4}{L}\right) \Bigg ]+i\Bigg [\frac{\phi ^2 \omega ^3 Pr_2}{L M Pr_1}\left( \frac{1}{Da}+2\delta ^2\right) \nonumber \\&\quad -2 \omega \delta ^2 \left( 1+\frac{\phi }{L}\right) \left( m^2 Q- \frac{\omega ^2Pr_2}{M^2 Pr_1^2}\right) -4 \delta ^6 \omega \left( \frac{\Lambda \phi }{ L}+\frac{1}{M \phi Pr_1}+\frac{\Lambda \phi Pr_2}{M Pr_1}\right) \nonumber \\&\quad + \delta ^2 \omega \left( \frac{2 \omega 62}{L M Pr_1}-\frac{3 \delta ^2 \phi }{Da L}-4 \delta ^4 \Lambda \right) +\phi \omega R_1 (q^2+\delta ^2)\left( \frac{1}{L}+\frac{Pr_2}{M Pr_1}\right) \nonumber \\&\quad + \omega \left( 1+\frac{\phi Pr_2}{M Pr_1}\right) \left( \frac{(q^2+\delta ^2)R_2}{L}+\frac{3\delta ^4}{Da}\right) , \nonumber \\ \Lambda _{3}&=q^2\left( \delta ^4-\frac{\phi ^2 \omega ^2 Pr_2}{L M Pr_1}\right) +i q^2 \delta ^2 \phi \omega \left( \frac{1}{L}+\frac{Pr_2}{M Pr_1}\right) , \nonumber \\ \Lambda _{4}&=-\frac{Q Pr_2}{4 M \pi ^2 Pr_1}e_1e_2e_3\left[ \frac{s_1}{e_3}\left( \frac{1}{e_6}\right) +\left( \frac{s_1}{2}+s_2\right) \left( \frac{1}{e_3^3}+\frac{1}{|e_3|^2}\right) \right] +\frac{R_1 q^2 }{4M^3}e_2e_3\left( \frac{1}{e_1}+\frac{1}{e_1^*}\right) \nonumber \\&\quad - \frac{R_2 q^2}{4 M^3L^3}e_1e_3\left( \frac{1}{e_2}+\frac{1}{e_2^*}\right) -\frac{Qm^2 \delta ^2}{4M}\left( \frac{Pr_2}{Pr_1}\right) ^2e_1e_2\left( \frac{1}{e_3}+\frac{1}{e_3^*}\right) , \nonumber \\ \Lambda _{5}&=-\frac{Q Pr_2}{Pr_1}e_1e_2e_3\left\{ \frac{1}{4 M \pi ^2}\left[ \frac{s_1}{e_3}\left( \frac{1}{e_3}+\frac{1}{e_3^*}\right) +(s_1+s_2)\left( \frac{1}{e_3^2}+\frac{1}{|e_3|^2}\right) \right] +\frac{1}{|e_3|^2e_6}\left( \frac{3s_1}{2}+s_2\right) \right\} \nonumber \\&\quad +\frac{R_1 q^2}{M}e_2e_3\left[ \frac{1}{4M^2}\left( \frac{1}{e_1}+\frac{1}{e_1^*}\right) +\frac{\pi ^2}{M^2e_1e_4}\right] -\frac{R_2 q^2}{M L}e_1e_3\left[ \frac{1}{4M^2 L^2}\left( \frac{1}{e_2}+\frac{1}{e_2^*}\right) +\frac{\pi ^2}{M^2 L^2 e_2e_5} \right] \nonumber \\&\quad -\frac{Q \delta ^2 Pr_2}{Pr_1}e_1e_2 \left[ \frac{m^2 Pr_2}{4 M Pr_1}\left( \frac{1}{e_3}+\frac{1}{e_3^*}\right) +\frac{m^2\pi ^2Pr_2}{Pr_1e_3e_6}\right] , \end{aligned}$$
(68)

where

$$\begin{aligned} e_1&=i \omega +\delta ^2, \quad e_4=i\omega +2\pi ^2, \quad s_1=-2m^2\pi ^4\frac{Pr_2}{Pr_1}, \\ e_2&=\frac{\phi }{L}\omega +\delta ^2, \quad e_5=\frac{\phi }{L}i\omega +2\pi ^2, \quad s_2=-l^2m^2\pi ^2\frac{Pr_2}{Pr_1}, \\ e_3&=\phi \frac{Pr_2}{Pr_1}i \omega +\delta ^2, \quad e_6=\phi \frac{Pr_2}{Pr_1}i \omega +2 M \pi ^2. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Babu, A.B., Rao, N.V.K. & Tagare, S.G. Weakly nonlinear thermohaline convection in a sparsely packed porous medium due to horizontal magnetic field. Eur. Phys. J. Plus 136, 795 (2021). https://doi.org/10.1140/epjp/s13360-021-01736-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01736-x

Keywords

Search

Navigation