A VDQ-transformed approach to the 3D compressible and incompressible finite hyperelasticity

Abstract

Based on the ideas of variational differential quadrature (VDQ) method and position transformation, an efficient numerical variational strategy is proposed in this paper to analyze the large deformations of hyperelastic structures in the context of three-dimensional (3D) compressible and incompressible nonlinear elasticity theories. Based on the minimum total potential energy principle together with the Neo-Hookean model, the governing equations are derived. The relations of paper are presented in novel vector–matrix format. Replacing the tensor form of formulations with matricized ones is a novelty of present work since the matricized formulations can be readily employed for the programming in numerical approaches. Discretizing is also carried out via VDQ operators. For applying the VDQ technique, the irregular domain of elements is transformed into a regular one by the method of mapping of position field based on the finite element shape functions. This feature enables the proposed VDQ-transformed approach to solve problems with irregular domains. Moreover, the developed formulation is simple, compact and easy to implement. Considering structures with various shapes, several illustrative convergence and comparative investigations are given to assess the performance of the approach in both compressible and incompressible regimes. Good accuracy and computational efficiency can be reported as the features of developed VDQ-based approach.

1 Introduction

The response of solids experiencing large deformations considering the influences of material nonlinearity has been always among important research topics in various fields. For describing the behavior of many materials, using linear elastic models leads to inaccurate results [1]. An important example is rubber for which the constitutive relation is given as nonlinearly elastic, isotropic, incompressible and generally independent of strain rate. Hyperelasticity offers an approach for modeling the stress–strain response of mentioned materials [2]. Also, modeling biological tissues (e.g. brain tissue) can be done by the hyperelasticity [3,4,5,6].

A literature review indicates that finding efficient numerical strategies to solve the problems of nonlinear elasticity is of great importance in the scope of computational mechanics. Several solution techniques were developed so far for addressing the problems in the context of compressible, nearly-incompressible and incompressible nonlinear elasticity. In particular, mixed finite element methods (FEMs) [7, 8] have been widely proposed by many researchers to this end. For example, Zdunek and Rachowicz [9] proposed a higher-order mixed finite element method for compressible transversely isotropic nonlinear hyperelasticity. In their three-field approach, displacement, fibre tension and fibre stretch were considered as independent variables. In another paper [10], they developed a Hu–Washizu-type three-field virtual work principle for strongly transversely isotropic compressible nonlinear hyperelasticity considering displacement, stretch and its energy conjugate uniaxial tension as independent variables. Typical applications in soft tissue biomechanics were also mentioned in that paper. Furthermore, these authors [11] developed a mixed hp-adaptive finite element method for anisotropic compressible nonlinear hyperelasticity considering reinforcement by two possibly oblique fibre groups. According to the Hellinger–Reissner principle, Viebahn et al. [12] proposed a mixed FE formulation for the linear elasticity which was validated for 2D and 3D cases. It has been revealed that the numerical inf–sup test is satisfied for both cases. In [13,14,15], by means of the Hilbert complexes of finite elasticity, compatible-strain mixed FEMs were proposed for some problems in the nonlinear elasticity. Angoshtari and his associates [13] considered a Hu–Washizu-type mixed formulation with the displacement, the displacement gradient, and the first Piola–Kirchhoff stress tensor as independent unknowns for the 2D compressible nonlinear elasticity. In another work, Faghih Shojaei and Yavari [14] developed a four-field mixed FE formulation within the framework of 2D incompressible nonlinear elasticity. Also, they extended their previous works to the 3D compressible and incompressible nonlinear elasticity in [15].

Moreover, the behavior of hyperelastic beams, plates and shells has been investigated in several research works. Amabili and his co-workers [4] developed a geometrically nonlinear theory for circular cylindrical shells made of incompressible hyperelastic materials. Also, the recent advances on the mechanics of soft shells including advanced problems of modeling human vessels (aorta) with fluid–structure interaction can be found in [5]. In another work, Amabili et al. [16] conducted experimental and numerical studies on the linear vibrations and nonlinear bending of a thin square silicon rubber plate. The theoretical part of study was based on the Mooney–Rivlin hyperelastic model. Wang and Wang [17] derived a relation for the critical stress values of a compressible slab made of a Murnaghan material by means of the combined series-asymptotic expansions method. It was concluded that the bifurcation type is dependent on the material constants and slab’s geometry. Anani and Rahimi [18] presented the stress analysis of rotating cylindrical shells made of isotropic FG rubber-like material, and derived exact analytical solution for stress components and displacements in the plane strain condition. Based on the finite elasticity and by a variational approach, a consistent finite-strain plate theory for incompressible hyperelastic materials was developed by Wang et al. [19]. For the nonlinear bending of hyperelastic incompressible plates, it was shown that the accuracy of solutions is O(h²). Also, Li and Dai [20] developed a dynamic finite-strain plate theory for incompressible hyperelastic materials. In another study, Li et al. [21] formulated a consistent finite-strain shell theory for incompressible hyperelastic materials.

Within a matrix formulation, Faghih Shojaei and Ansari [22] introduced a numerical method called as variational differential quadrature (VDQ) through which the discretized governing equations can be derived directly without analytical derivation of the strong form of governing equations. In [22], based on the first-order shear deformation plate theory, the geometrically nonlinear bending problem of plates was investigated, and it was indicated that VDQ has a faster convergence rate in comparison with FEM. Additionally, there is no locking problem in VDQ as it does not require any shape function. No need to assemblage process is another advantage of VDQ which results in its simple application. Based upon these features, the VDQ method has been extensively employed in several papers up to now (e.g. [23,24,25,26,27]). Also, within the framework of hyperelasticity, the application of this technique has been recently proposed by Hassani et al. [28,29,30,31]. In [28], a VDQ-based three-field approach was developed to analyze the large deformations of hyperelastic bodies in the context of 2D finite elasticity. Based on the same technique, a single-field approach was also developed in [29] based on the compressible nonlinear elasticity. In [30], they extended the approach to the micromorphic hyperelasticity.

In the current paper, using the combination of VDQ and position transformation ideas, a numerical method is developed to analyze the large deformations of 3D arbitrary-shaped hyperelastic bodies based on both compressible and incompressible nonlinear elasticity. The tensor form of equations is replaced by a novel matrix–vector format. Based on this feature, the formulation can be readily used in the coding process of numerical methods. By combining the VDQ method with the mapping idea of finite element method, an approach is proposed which is able to consider hyperelastic problems with irregular and 3D domains. Moreover, the Neo-Hookean model is utilized to describe the hyperelastic character of material. In order to apply the VDQ method for irregular-shaped structures, the irregular domain is transformed into a regular one using the interpolation of position field (mapping). Several benchmark examples are presented to test the proposed formulation in both compressible and incompressible regimes.

2 Numerical solution strategy

Here, the equations in tensor form are written in vector–matrix form for computational goals. Then, the vector–matrix relations are discretized on space domain. Accordingly, compact relations are achieved which can be utilized in programming in an efficient way. The details of discretization have been given in [22, 28,29,30,31]. Moreover, the processes of discretization, VDQ derivation and integration are explained in Appendix.

2.1 Kinematic relations

The discretized from of displacement vector is given by

$$ {\mathbb{U}} = \left[\hspace{-4pt}\left[ {{\mathbf{U}} } \right]\hspace{-4pt}\right]_{{{\mathfrak{C}}_{0} }} = \left\lbrack\hspace{-4pt}\left\lbrack\left[{\begin{array}{*{20}c} {U_{1} } \\ {U_{2} } \\ {U_{3} } \\ \end{array} } \right]\right\rbrack\hspace{-4pt}\right\rbrack_{{{\mathfrak{C}}_{0} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{1} } \\ {{\mathbf{U}}_{2} } \\ {{\mathbf{U}}_{3} } \\ \end{array} } \right] $$

(1)

The unknown vector is also introduced as follows

$${\mathbb{d}}={\mathbb{U}}$$

(2)

The displacement gradient tensor in vector–matrix form is written as

$$ {\mathbf{H}} = \nabla_{{\mathbf{X}}} \left( {\mathbf{U}} \right) = \frac{{\partial {\mathbf{U}}}}{{\partial {\mathbf{X}}}} = \frac{{\partial U_{i} }}{{\partial X_{I} }}{\mathbf{e}}_{i} \otimes {\mathbf{e}}_{I} , H_{iI} = \frac{{\partial U_{i} }}{{\partial X_{I} }} = U_{i,I} , $$

(3a)

$$ \begin{aligned} {\hat{\mathbf{H}}} & = \left\lceil {\mathbf{H}} \right\rceil_{1} = \left[ {\begin{array}{*{20}c} {H_{11} } & {H_{21} } & {H_{31} } & {H_{12} } & {H_{22} } & {H_{32} } & {H_{13} } & {H_{23} } & {H_{33} } \\ \end{array} } \right]^{{\text{T}}} \\ & = \left[ {\begin{array}{*{20}c} {U_{1,1} } & {U_{2,1} } & {U_{3,1} } & {U_{1,2} } & {U_{2,2} } & {U_{3,2} } & {U_{1,3} } & {U_{2,3} } & {U_{3,3} } \\ \end{array} } \right]^{{\text{T}}} = \left[ {\begin{array}{*{20}l} {{\mathbf{I}}_{3} \,{ \circledast }\,\partial_{{X_{1} }} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,\partial_{{X_{2} }} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,\partial_{{X_{3} }} } \\ \end{array} } \right]{\mathbf{U}} = {\mathbf{E}}_{{\mathbf{H}}} {\mathbf{U}}, \\ \end{aligned} $$

(3b)

$$ {\mathbf{E}}_{{\mathbf{H}}} = \left[ {\begin{array}{*{20}l} {{\mathbf{I}}_{3}\, { \circledast }\,\partial_{{X_{1} }} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,\partial_{{X_{2} }} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,\partial_{{X_{3} }} } \\ \end{array} } \right] $$

(3c)

After discretization one has

$$\widehat{\mathbb{H}}={\left[\kern-0.15em\left[\widehat{\mathbf{H}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}={\mathbb{E}}_{\mathbf{H}}{\mathbb{d}}_{\mathbf{U}}$$

(4a)

$${\mathbb{E}}_{{\mathbf{H}}} = \left[\kern-0.15em\left[{{\mathbf{E}}_{{\mathbf{H}}}}\right]\kern-0.15em\right]_{{{\mathfrak{C}}_{0} }}= \left[ {\begin{array}{*{20}l}{{\mathbf{I}}_{3}\, { \circledast }\,{\mathop{\mathop{\varvec{\mathcal{D}}}\limits^{3d}}\nolimits_{X_{1}}} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,{\mathop{\mathop{\varvec{\mathcal{D}}}\limits^{3d}}\nolimits_{X_{2}}} } \\ {{\mathbf{I}}_{3}\, { \circledast }\,{\mathop{\mathop{\varvec{\mathcal{D}}}\limits^{3d}}\nolimits_{X_{3}}} } \\ \end{array} } \right]$$

(4b)

Where ${\lceil{\blacksquare}_{1}\rceil}_{{\blacksquare}_{2}}$ signifies an operator which reduces a tensor with arbitrary order of ${\blacksquare}_{1}$ to a tensor with the order of ${\blacksquare}_{2}$. Besides, ${\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{1}}$, ${\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{2}}\boldsymbol{ }\,\,\mathrm{and }\,\,{\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{3}}$ are the VDQ first-order derivative operators with respect to ${X}_{1}$, ${X}_{2}$ and ${X}_{3}$ for a 3D domain [28,29,30,31]. The deformation gradient tensor is defined as

$$ {\mathbf{F}} = {\text{Grad}}\left( {\mathbf{x}} \right) = \nabla_{{\mathbf{X}}} \left( {\mathbf{x}} \right) = \nabla_{{\mathbf{X}}} \left( {\mathbf{X}} \right) + \nabla_{{\mathbf{X}}} \left( {\mathbf{U}} \right) = {\mathbf{I}}_{3} + {\mathbf{H}} $$

(5a)

whose vector–matrix representation is

$$ \begin{aligned} {\hat{\mathbf{F}}} = \left\lceil {\mathbf{F}} \right\rceil_{1} & = \left[ {\begin{array}{*{20}c} {F_{11} } & {F_{21} } & {F_{31} } & {F_{12} } & {F_{22} } & {F_{32} } & {F_{13} } & {F_{23} } & {F_{33} } \\ \end{array} } \right]^{T} \\ & = \left\lceil {{\mathbf{I}}_{3} + {\mathbf{H}} } \right\rceil_{1} = {\hat{\mathbf{I}}}_{3} + {\hat{\mathbf{H}}} \\ \end{aligned} $$

(5b)

$$ {\mathbf{I}}_{3} = \left\lceil {{\mathbf{I}}_{3} } \right\rceil_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ \end{array} } \right]^{{\text{T}}} $$

(5c)

Using the discretization operator leads to

$$ \hat{\mathbb{F}} = \left[\kern-0.15em\left[ {{\hat{\mathbf{F}}}} \right]\kern-0.15em\right]_{{{\mathfrak{C}}_{0} }} = \left[\kern-0.15em\left[ {{\hat{\mathbf{I}}}_{3} + {\hat{\mathbf{H}}}} \right]\kern-0.15em\right]_{{{\mathfrak{C}}_{0} }} = \hat{\mathbb{I}}_{3} + \hat{\mathbb{H}} $$

(6a)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\widehat{\mathbb{F}}}={\langle {\left[\kern-0.15em\left[ {\widehat{\mathbf{F}}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}={\left[\begin{array}{ccccccccc}\langle {\widehat{\mathbf{F}}}_{1}\rangle & \langle {\widehat{\mathbf{F}}}_{2}\rangle & \langle {\widehat{\mathbf{F}}}_{3}\rangle & \langle {\widehat{\mathbf{F}}}_{4}\rangle & \langle {\widehat{\mathbf{F}}}_{5}\rangle & \langle {\widehat{\mathbf{F}}}_{6}\rangle & \langle {\widehat{\mathbf{F}}}_{7}\rangle & \langle {\widehat{\mathbf{F}}}_{8}\rangle & \langle {\widehat{\mathbf{F}}}_{9}\rangle \end{array}\right]}^{\mathrm{T}}$$

(6b)

$$\hat{\mathbb{I}}_{3} = \left[\kern-0.15em\left[ {{\hat{\mathbf{I}}}_{3} } \right]\kern-0.15em\right]_{{{\mathfrak{C}}_{0} }} = {\hat{\mathbf{I}}}_{3} { \circledast }1_{n*1} $$

(6c)

where $\langle \mathbf{A}\rangle$ shows the diagonal of vector $\mathbf{A}$. Furthermore, ${\langle {\mathbb{B}}\rangle }_{\mathbb{b}}$ shows each block diagonal of block matrix ${\mathbb{B}}$.

2.2 Compressible regime relations

2.2.1 Basic relations

Based on the compressible Neo-Hookean model, the strain energy density function is expressed as

$$ w_{0} \left( {I_{1} ,I_{3} } \right) = \frac{\mu }{2}\left( {I_{1} - 3} \right) - \frac{\mu }{2}\ln I_{3} + \frac{\kappa }{2}\left( {I_{3}^{1/2} - 1} \right)^{2} $$

(7a)

where ${I}_{1}$ and ${I}_{3}$ are the first and third invariants of right Cauchy–Green tensor given by

$$ I_{1} = {\text{tr}}\left( {\mathbf{C}} \right) = {\text{tr}}\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{F}}} \right) = {\mathbf{F}} :{\mathbf{F}} = {\hat{\mathbf{F}}} \cdot {\hat{\mathbf{F}}} = {\hat{\mathbf{F}}}^{{\text{T}}} {\hat{\mathbf{F}}} $$

(7b)

$$ I_{3} = \det \left( {\mathbf{C}} \right) = \det \left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{F}}} \right) = \det \left( {{\mathbf{F}}^{{\text{T}}} } \right)\det \left( {\mathbf{F}} \right) = J^{2} $$

(7c)

Also, for the deformation Jacobian and its derivative, which are used in the calculations of stress tensor and elasticity modulus, one has

$$ J = \det \left( {\mathbf{F}} \right) = F_{11} \left( {F_{22} F_{33} - F_{23} F_{32} } \right) - F_{12} \left( {F_{21} F_{33} - F_{23} F_{31} } \right) + F_{13} \left( {F_{21} F_{32} - F_{22} F_{31} } \right) $$

(7d)

$$ J_{{,{\mathbf{F}}}} = \frac{\partial J}{{\partial {\mathbf{F}}}} = J{\mathbf{F}}^{{ - {\text{T}}}} , $$

(7e)

$$ J_{{,{\mathbf{FF}}}} = \frac{{\partial J_{{,{\mathbf{F}}}} }}{{\partial {\mathbf{F}}}} = J{\mathbf{F}}^{{ - {\text{T}}}} \otimes {\mathbf{F}}^{{ - {\text{T}}}} - J{\mathbf{F}}^{ - 1} \,\, \underline { \otimes } \,\, {\mathbf{F}}^{{ - {\text{T}}}} $$

(7g)

in which

$$ \left\{ {\begin{array}{*{20}c} {A \, \otimes \, B = A_{ij} B_{kl} {\mathbf{e}}_{i} \otimes {\mathbf{e}}_{j} \otimes {\mathbf{e}}_{k} \otimes {\mathbf{e}}_{l} } \\ {A \, \overline{ \otimes } \, B = A_{ik} B_{jl} {\mathbf{e}}_{i} \otimes {\mathbf{e}}_{j} \otimes {\mathbf{e}}_{k} \otimes {\mathbf{e}}_{l} } \\ {A \, \underline { \otimes } \, B = A_{il} B_{jk} {\mathbf{e}}_{i} \otimes {\mathbf{e}}_{j} \otimes {\mathbf{e}}_{k} \otimes {\mathbf{e}}_{l} } \\ \end{array} } \right., $$

(7h)

It should be noted that the vector–matrix and discretized forms of Eq. (7) ($J,{J}_{,\widehat{\mathbf{F}}},{J}_{,\widehat{\mathbf{F}}\widehat{\mathbf{F}}}$ and ${\mathbb{J}},{\mathbb{J}}_{,\widehat{\mathbb{F}}},{\mathbb{J}}_{,\widehat{\mathbb{F}}\widehat{\mathbb{F}}}$), which will be used in the following calculations of stress and elasticity modulus, are given in Appendix.

The stress tensor is accordingly defined as follows

$$ {\mathbf{P}} = \frac{{\partial w_{0} }}{{\partial {\mathbf{F}}}} = \mu \left( {{\mathbf{F}} - {\mathbf{F}}^{{ - {\text{T}}}} } \right) + \kappa \left( {J^{2} - J} \right){\mathbf{F}}^{{ - {\text{T}}}} , $$

(8a)

with the following vector–matrix format

$$ \begin{aligned} {\hat{\mathbf{P}}} = \left\lceil {\mathbf{P}} \right\rceil _{1} & = \left[ {\begin{array}{*{20}c} {P_{11} } & {P_{21} } & {P_{31} } & {P_{12} } & {P_{22} } & {P_{32} } & {P_{13} } & {P_{23} } & {P_{33} } \\ \end{array} } \right]^{{\text{T}}} = \left\lceil {\frac{{\partial w_{0} }}{{\partial {\mathbf{F}}}}} \right\rceil_{1} = \frac{{\partial w_{0} }}{{\partial {\hat{\mathbf{F}}}}} \\ & = \frac{{\partial w_{0} }}{{\partial I_{1} }}\frac{{\partial I_{1} }}{{\partial {\hat{\mathbf{F}}}}} + \frac{{\partial w_{0} }}{{\partial I_{3} }}\frac{{\partial I_{3} }}{{\partial {\hat{\mathbf{F}}}}} = \mu {\hat{\mathbf{F}}} + \left( { - \frac{\mu }{J} + \kappa \left( {J - 1} \right)} \right)J_{{,{\hat{\mathbf{F}}}}} \\ \end{aligned} $$

(8b)

In the discretized form one also has

$$\hat{\mathbb{P}} = \left[\kern-0.15em\left[ {{\hat{\mathbf{P}}}} \right]\kern-0.15em\right]_{{{\mathfrak{B}}_{0} }} = \mu \hat{\mathbb{F}} + \left( {{\mathbf{I}}_{9} \, { \circledast } \, \langle\kappa \left( {{\mathbb{J}} - 1} \right) - \mu {\mathbb{J}}^{ \circ - 1} }\rangle \right){\mathbb{J}}_{,\hat{\mathbb{F}}} $$

(8c)

where $\circ$ denotes the Hadamard product. The tangent modulus is also formulated as

$$ \begin{aligned} {\mathbf{M}} = \frac{{\partial {\mathbf{P}}}}{{\partial {\mathbf{F}}}} & = \mu {\mathbf{I}}_{2} \overline{ \otimes }{\mathbf{I}}_{2} + \left( {\mu - \kappa \left( {J^{2} - J} \right)} \right){\mathbf{F}}^{{ - {\text{T}}}} \underline { \otimes } {\mathbf{F}}^{ - 1} \\ & \quad + \kappa \left( {2J^{2} - J} \right){\mathbf{F}}^{{ - {\text{T}}}} \otimes {\mathbf{F}}^{{ - {\text{T}}}} \\ \end{aligned} $$

(9a)

The vector–matrix representation of tangent modulus is

$$ \begin{aligned} {\hat{\mathbf{M}}} = \left\lceil {\mathbf{M}} \right\rceil_{2} & = \left[ {\begin{array}{*{20}l} {M_{1111} } & {M_{1121} } & \cdots & {M_{1133} } \\ {M_{2111} } & {M_{2121} } & \cdots & {M_{2133} } \\ \vdots & \vdots & {} & \vdots \\ {M_{3311} } & {M_{3321} } & \cdots & {M_{3333} } \\ \end{array} } \right] = \left\lceil {\frac{{\partial {\mathbf{P}}}}{{\partial {\mathbf{F}}}}} \right\rceil_{2} = \frac{{\partial {\hat{\mathbf{P}}}}}{{\partial {\hat{\mathbf{F}}}}} \\ & = \mu {\mathbf{I}}_{9} + \left( {\kappa + \frac{\mu }{{J^{2} }}} \right)J_{{,{\hat{\mathbf{F}}}}} J_{{,{\hat{\mathbf{F}}}}}^{{\text{T}}} + \left( {\kappa \left( {J - 1} \right) - \frac{\mu }{J}} \right)J_{,{\hat{\mathbf{F}}}{\hat{\mathbf{F}}}} \\ \end{aligned} $$

(9b)

Also, the discretized form is given by

$$ \hat{\mathbb{M}} = \left[\kern-0.15em\left[ {{\hat{\mathbf{M}}}} \right]\kern-0.15em\right]\user2{ }_{{{\mathfrak{C}}_{0} }} = \mu {\mathbf{I}}_{9n} + \left( {{\mathbf{I}}_{9} { \circledast }\langle {\kappa + \mu {\mathbb{J}}^{ - \circ 2} } \rangle} \right){\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}}}\limits^{\smile}}{\mathbb{J}}_{{,{\hat{\mathbb{F}}}}}^{{\text{T}}} + \left( {{\mathbf{I}}_{9} { \circledast } \langle{\kappa ( {{\mathbb{J}} - 1} ) - \mu {\mathbb{J}}^{ \circ - 1} } \rangle} \right){\mathbb{J}}_{{,{\hat{\mathbb{F}}\hat{\mathbb{F}}}}}$$

(9c)

The stress increment can be expressed as

$$ \Delta {\mathbf{P}}\left( {\mathbf{F}} \right) = \frac{{\partial {\mathbf{P}}}}{{\partial {\mathbf{F}}}} :\Delta {\mathbf{F}} = {\mathbf{M}} :\Delta {\mathbf{F}} = {\mathbf{M}} :\Delta {\mathbf{H}}, $$

(10a)

whose vector–matrix and discretized forms are as follows:

$$ \Delta {\hat{\mathbf{P}}} = \left\lceil {\Delta {\mathbf{P}} } \right\rceil_{1} = \left\lceil {{\mathbf{M}} :\Delta {\mathbf{F}} } \right\rceil_{1} = \left\lceil {{\mathbf{M}} } \right\rceil_{2} \left\lceil {\Delta {\mathbf{F}} } \right\rceil_{1} = {\hat{\mathbf{M}}}\Delta {\hat{\mathbf{F}}} = {\hat{\mathbf{M}}}\Delta {\hat{\mathbf{H}}} = {\hat{\mathbf{M}}\mathbf{E}}_{{\mathbf{H}}} {\mathbf{U}}, $$

(10b)

$$\Delta \widehat{\mathbb{P}}={\left[\kern-0.15em\left[ {\Delta \widehat{\mathbf{P}}} \right]\kern-0.15em\right] }_{{\mathfrak{C}}_{0}}= {\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}\Delta \widehat{\mathbb{H}}= {\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}{\mathbb{E}}_{\mathbf{H}}\Delta {\mathbb{d}}_{\mathbf{U}},$$

(10c)

$${\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}={\langle \widehat{\mathbb{M}}\rangle }_{\mathbb{b}}=\mu {\mathbf{I}}_{9n}+\left({\mathbf{I}}_{9}\circledast\langle \kappa +\mu {\mathbb{J}}^{-\circ 2}\rangle \right){\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}}}\limits^{\smile}}{\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}}}\limits^{{\smile}}}^{\mathrm{T}}+\left({\mathbf{I}}_{9}\circledast\langle\kappa \left({\mathbb{J}}-1\right)-\mu {\mathbb{J}}^{\circ -1}\rangle \right){\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}\hat{\mathbb{F}}}}\limits^{\smile}},$$

(10d)

It is worth mentioning that for implementing various numerical techniques, it is necessary to compute all elements of stress and elasticity modulus tensors at all computational points. Applying the 3D and higher-order tensorial relations of (7), (8a) and (9a) is difficult due to the existence of complicated tensor products and the inverse of deformation gradient tensor. Furthermore, using these relations in the programming is difficult that necessitates the use of nested loops. In the present work, with applying reduction and discretization processes, the aforementioned tensor relations are reduced to compact and efficient relations of (A15)–(A17), (8c) and (9c) in a systematic and operator-based manner whose application in the programming is simple and straightforward.

2.2.2 Minimum total potential energy principle

2.2.2.1 Internal energy term

The strain energy is first formulated in the following.

• Potential energy and its variation in tensor representation

  $${\Pi }^{int}={\int }_{{\mathfrak{C}}_{0}}{w}_{0}\left(\mathbf{F}\right)d{\forall }_{0}$$

  (11a)
  $$\delta {\Pi }^{int}={\int }_{{\mathfrak{C}}_{0}}\delta {w}_{0}d{\forall }_{0}={\int }_{{\mathfrak{C}}_{0}}\left(\frac{\partial {w}_{0}}{\partial \mathbf{F}}:\delta \mathbf{F}\right)d{\forall }_{0}={\int }_{{\mathfrak{C}}_{0}}\left(\mathbf{P}:\delta \mathbf{F}\right)d{\forall }_{0}$$

  (11b)

• Variation of potential energy in vector–matrix format

  $$\delta {\Pi }^{int}={\int }_{{\mathfrak{C}}_{0}}\left(\widehat{\mathbf{P}}\cdot \delta \widehat{\mathbf{F}}\right)d{\forall }_{0}={\int }_{{\mathfrak{C}}_{0}}\left(\delta {\widehat{\mathbf{F}}}^{\mathrm{T}}\widehat{\mathbf{P}}\right)d{\forall }_{0}={\int }_{{\mathfrak{C}}_{0}}\left(\delta {\widehat{\mathbf{H}}}^{\mathrm{T}}\widehat{\mathbf{P}}\right)d{\forall }_{0}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}{ \left[\kern-0.15em\left[ {\delta {\widehat{\mathbf{H}}}^{\mathrm{T}}\widehat{\mathbf{P}}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}=\delta {\mathbb{d}}^{\mathrm{T}}{\mathbb{F}}_{int},$$

  (11c)
  $${\mathbb{F}}_{int}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast \langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right)\widehat{\mathbb{P}},$$

  (11d)

2.2.2.2 External energy term

The relations of external energy are also given as

$${\Pi }^{ext}={\int }_{{\mathfrak{C}}_{0}}\mathbf{U}\cdot {\mathbf{b}}_{0} d{\forall}_{0}+{\int }_{\partial {\mathfrak{ C}}_{0}^{\mathbf{t}}}\mathbf{U}\cdot {\mathbf{t}}_{0}d{A}_{0}$$

(12a)

$$\begin{aligned} &\delta {\Pi }^{ext}={\int }_{{\mathfrak{C}}_{0}}\delta \mathbf{U}\cdot {\mathbf{b}}_{0} d{A}_{0} +{\int }_{\partial {\mathfrak{C}}_{0}^{\mathbf{t}}}\delta \mathbf{U}\cdot {\mathbf{t}}_{0}d{S}_{0} ={\int }_{{\mathfrak{C}}_{0}}\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{b}}_{0} d{A}_{0}+{\int }_{\partial {\mathfrak{C}}_{0}^{\mathbf{t}}}\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{t}}_{0}d{S}_{0} \\ &={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}{\left[\kern-0.15em \left[ {\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{b}}_{0}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}+{\stackrel{2d}{\varvec{\mathcal{S}}}_{{X_1X_2};\partial {\mathfrak{C}}_{0}^{\mathbf{t}}}}{ \left[\kern-0.15em\left[ {\delta {\mathbf{U}}^{\mathrm{T}}{\mathbf{t}}_{0}} \right]\kern-0.15em\right]}_{\partial {\mathfrak{C}}_{0}^{\mathbf{t}}} =\delta {\mathbb{d}}^{\mathrm{T}}{\mathbb{F}}_{ext} \end{aligned} $$

(12b)

where

$${\mathbb{F}}_{ext}={\mathbb{F}}^{bf}+{\acute{\mathbb{F}}}^{df}$$

(12c)

$${\mathbb{F}}^{bf}=\left({\mathbf{I}}_{3}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right){\mathbb{b}}_{0}$$

(12d)

$${\acute{\mathbb{F}}}^{{df}} = {\text{expand}}\,\,({\mathbb{F}}^{{df}}),$$

(12e)

$${\mathbb{F}}^{df}=\left({\mathbf{I}}_{3}\circledast\langle {\stackrel{2d}{\varvec{\mathcal{S}}}}_{X_1X_2;\partial{\mathfrak{C}}_{i}^{\textbf{t}}}\rangle \right){\mathbb{t}}_{0},$$

(12f)

$${\mathbb{t}}_{0}= \left[\kern-0.15em\left[ {{\mathbf{t}}_{0} } \right]\kern-0.15em\right]_{{\partial{\mathfrak{C}}_{0}^{{\mathbf{t}}} }},$$

(12g)

2.2.2.3 Virtual work principle

This principle states that

$$\Pi ={\Pi }^{int}-{\Pi }^{ext},$$

(13)

$$\delta \Pi =\delta {\Pi }^{int}-\delta {\Pi }^{ext}= {\varvec{0}},$$

Based on Eqs. (11c) and (12b) and considering that the elements of $\delta {\mathbb{d}}$ have arbitrary value, the following set of algebraic nonlinear governing equations is derived

$$\delta {\mathbb{d}}^{\mathrm{T}}{\mathbb{F}}_{int}-\delta {\mathbb{d}}^{\mathrm{T}}{\mathbb{F}}_{ext}=\delta {\mathbb{d}}^{\mathrm{T}}\left({\mathbb{F}}_{int}-{\mathbb{F}}_{ext}\right)={\varvec{0}}$$

(14)

$${\mathbb{F}}_{int}-{\mathbb{F}}_{ext}={\varvec{0}},$$

(15)

2.2.3 Newton–Raphson method

In this sub-section, solving the nonlinear problem is done by the Newton–Raphson method. For this purpose, linearization and repetitive processes are formulated in the following

$${\mathbb{R}}\left({\mathbb{d}}\right)={\varvec{0}}$$

(16a)

$${\mathbb{R}}^{i+1}={\mathbb{R}}^{i}+\Delta{\mathbb{R}} ={\mathbb{R}}^{i}+\Delta{\mathbb{R}}={\mathbb{R}}^{i}+{\mathbb{K}}^{t}\Delta {\mathbb{d}} \stackrel{{\mathbb{R}}^{i+1}={\varvec{0}}}{\Rightarrow } -{\mathbb{R}}^{i}={\mathbb{K}}^{t}\left({\mathbb{d}}^{i+1}-{\mathbb{d}}^{i}\right)$$

(16b)

$${\mathbb{d}}^{i+1}={\mathbb{d}}^{i}-{\left({\mathbb{K}}^{t}\right)}^{-1}{\mathbb{R}}^{i},$$

(16c)

Based upon Eq. (15), the governing residual vector is defined as

$${\mathbb{R}}={\mathbb{F}}_{int}-{\mathbb{F}}_{ext}={\varvec{0}},$$

(17)

Considering Eqs. (11d) and (12c), the tangent stiffness matrix (Jacobian) is obtained as

$$\Delta {\mathbb{R}}=\Delta \left({\mathbb{F}}_{int}-{\mathbb{F}}_{ext}\right)=\Delta {\mathbb{F}}_{int}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right)\Delta \widehat{\mathbb{P}}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right){\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}{\mathbb{E}}_{\mathbf{H}}\Delta {\mathbb{d}}={\mathbb{K}}^{t}\Delta {\mathbb{d}}$$

(18)

$${\mathbb{K}}^{t}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right) {\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}{\mathbb{E}}_{\mathbf{H}}$$

(19)

2.3 Incompressible regime relations

For the incompressible regime, the strain energy density is expressed as

$${w}_{0}\left({I}_{1},p\right)=\frac{\mu }{2}\left({I}_{1}-3\right)+p\left(J-1\right),$$

(20a)

In Eq. (20a), the pressure-like parameter ($p$), as Lagrange’s coefficient, imposes the incompressibility constraint ($J=1$) on the problem. This parameter is among the unknowns of problems. The final unknown vector, which includes the values of displacement field and pressure at all computational points, is thus defined as follows

$${\mathbb{d}}={\left[\hspace{-4pt}\left[ {\left[\begin{array}{c}{\textbf{U}}\\ p\end{array}\right]} \right]\hspace{-4pt}\right]}_{{\mathfrak{C}}_{0}}=\left[\begin{array}{c}{\mathbb{U}}\\ {\mathbb{p}}\end{array}\right]$$

(20b)

Also, the variational form of internal energy corresponding to this regime can be computed as

$$\delta {\Pi }^{int}={\int }_{{\mathfrak{C}}_{0}}\delta {w}_{0}\left(\mathbf{F},p\right)d{\forall }_{0}={\int }_{{\mathfrak{C}}_{0}}\left(\mathbf{P}:\delta \mathbf{F}+\delta p\left(J-1\right)\right)d{\forall }_{0}=\delta {\mathbb{U}}^{\mathrm{T}}{\mathbb{F}}_{\mathbf{U}}^{int}+\delta {\mathbb{p}}^{\mathrm{T}}{\mathbb{F}}_{p},$$

(21a)

$${\mathbb{F}}_{\mathbf{U}}^{int}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right)\widehat{\mathbb{P}}, {\mathbb{F}}_{p}^{int}=\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \left({\mathbb{J}}-1\right),$$

(21b)

in which

$$\widehat{\mathbb{P}}={\left[\kern-0.15em\left[ {{\lceil\mathbf{P}\rceil}_{1}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}=\mu \widehat{\mathbb{F}}+\left({\mathbf{I}}_{9}\circledast\langle {\mathbb{p}}\rangle \right){\mathbb{J}}_{,\widehat{\mathbb{F}}}$$

(22)

Now, by substituting the obtained relations in the virtual work principle, the following set of nonlinear governing equations in the incompressible regime is derived

$$\delta \Pi =\delta {\Pi }^{int}-\delta {\Pi }^{ext}=\delta {\mathbb{U}}^{\mathrm{T}}\left({\mathbb{F}}_{\mathbf{U}}^{int}-{\mathbb{F}}_{\mathbf{U}}^{ext}\right)+\delta {\mathbb{p}}^{\mathrm{T}}{\mathbb{F}}_{p}^{int}={\varvec{0}}$$

(23)

$$\left\{ \begin{gathered} {\mathbb{F}}_{{\mathbf{U}}}^{{int}} - {\mathbb{F}}_{{\mathbf{U}}}^{{ext}} = 0 \hfill \\ {\mathbb{F}}_{p}^{{int}} = 0~ \hfill \\ \end{gathered} \right.$$

where ${\mathbb{F}}_{p}=0$ is the algebraic set of equations corresponding to the incompressibility constraint which must be solved in conjunction with the set of governing equations. Hence, on the basis of the Newton–Raphson method, the residual vector and tangent stiffness matrix used for the linearization of obtained set of equations are calculated as

$${\mathbb{R}}=\left[\begin{array}{c}{\mathbb{R}}_{1}\\ {\mathbb{R}}_{2}\end{array}\right]=\left[\begin{array}{c}{\mathbb{F}}_{\mathbf{U}}^{int}-{\mathbb{F}}_{\mathbf{U}}^{ext}\\ {\mathbb{F}}_{p}^{int}\end{array}\right]={\varvec{0}}$$

(24a)

$$\Delta {\mathbb{R}}=\left[\begin{array}{c}\Delta {\mathbb{R}}_{1}\\ \Delta {\mathbb{R}}_{2}\end{array}\right]={\mathbb{K}}^{t}\Delta {\mathbb{d}},$$

(24b)

$${\mathbb{K}}^{t}=\left[\begin{array}{cc}{\mathbb{K}}_{\mathbf{U}\mathbf{U}}^{t}& {\mathbb{K}}_{\mathbf{U}p}^{t}\\ {\mathbb{K}}_{p\mathbf{U}}^{t}& {\varvec{0}}\end{array}\right],$$

(25a)

$${\mathbb{K}}_{\mathbf{U}\mathbf{U}}^{t}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right){\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}_{\mathbf{P}\mathbf{F}}{\mathbb{E}}_{\mathbf{H}}$$

(25b)

$${\mathbb{K}}_{\mathbf{U}p}^{t}={\mathbb{E}}_{\mathbf{H}}^{\mathrm{T}}\left({\mathbf{I}}_{9}\circledast\langle {\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3};{\mathfrak{C}}_{0}}\rangle \right){\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}_{\mathbf{P}p},$$

(25c)

$${\mathbb{K}}_{p\mathbf{U}}^{t}={{\mathbb{K}}_{\mathbf{U}p}^{t}}^{\mathrm{T}},$$

(25d)

where

$${{\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}}_{\mathbf{P}\mathbf{F}}={\langle {\left[\kern-0.15em\left[{\lceil\frac{\partial \mathbf{P}}{\partial \mathbf{F}}\rceil}_{2}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}=\mu {\mathbb{I}}_{9}+\left({\mathbf{I}}_{9}\circledast\langle {\mathbb{p}}\rangle \right){\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}\hat{\mathbb{F}}}}\limits^{\smile}}, {{\mathop{\widehat{\mathbb{M}}}\limits^{\smile}}}_{\mathbf{P}p}={\left\langle {\left[\kern-0.15em\left[{\lceil\frac{\partial \mathbf{P}}{\partial p}\rceil}_{1}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\right\rangle }_{\mathbb{b}}={\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}\hat{\mathbb{F}}}}\limits^{\smile}},$$

(26)

3 Numerical examples

3.1 Cantilever beam

As the first example, a cantilever beam under shearing force in the compressible regime is considered which is schematically shown in Fig. 1. Table 1 indicates the variation of horizontal displacement of point ${\varvec{A}}$ with the number of nodes for various values of shearing force. Also, a comparison is made in this table between the present results and those given in [32]. The convergence and accuracy of the present results can be clearly seen from Table 1. Moreover, the deformed configurations for various numbers of nodes are shown in Fig. 2.

Fig. 1

Schematic of cantilever beam example

Table 1 Variation of horizontal displacement of point ${\varvec{A}}$ of cantilever beam under shearing force in the compressible regime with the number of nodes for various values of shearing force ($\left[\kappa ,\mu \right]=\left[\mathrm{24000,6000}\right]MPa$)

Fig. 2

Deformed configurations of cantilever beam under shearing force in the compressible regime ($f$ $= 0.1N/m{m}^{2}, \left[\kappa ,\mu \right]=\left[\mathrm{24000,6000}\right]MPa)$

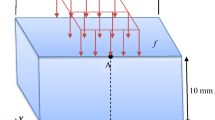
3.2 Rectangular block

In this example, a block subjected to compression shown in Fig. 3 is considered. The block is assumed to be under compression whose length and width is 2 mm and its height is 1 mm. The loading square surface on the upper face of the block has an edge of 1 mm and is subjected to a traction $\overline{T }=(\mathrm{0,0},f)$. The vertical (horizontal) displacement at the bottom (top) of the block is zero. By means of symmetry, only a quarter of the block is considered as indicated in Fig. 3. The material properties are assumed as.

Fig. 3

Schematic of the rectangular block example

$$\begin{aligned}&\mu = 80.194\, \mathrm{MPa} ; \,\,\kappa = 120.291 \mathrm{MPa}\,{\text{for\,compressible\,regime.}}\\&\mu = 80.194\, \mathrm{MPa} \,{\text{for\,incompressible\,regime.}}\end{aligned}$$

Figure 4 indicates the variation of vertical displacement of point A of the block against the number of nodes for various values of normal force f in the compressible and incompressible regimes. Also, comparisons are made between the present computations and those provided by Elguedj et al. [33]. Again, it is observed that using the proposed VDQ-based approach leads to converged and accurate results. Also, the deformed configurations for various numbers of nodes are represented in Fig. 5 for compressible block.

Fig. 4

Variation of vertical displacement of point ${\varvec{A}}$ of the block under compression in the compressible and incompressible regimes with the number of nodes for various values of distributed force ($\left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]MPa$ for compressible, $\mu =80.194MPa$ for incompressible)

Fig. 5

Deformed configurations of the block under compression in the compressible regime ($f=200\,{\text{N/m{m}}}^{2}, \left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]\,{\text{MPa}})$

3.3 Cook’s membrane

The Cook’s membrane problem as a well-known problem is solved in this example (Fig. 6). According to the figure, the shown 3D structure has a trapezoidal surface which is clamped from one side and it is loaded by a surface traction load. In the compressible regime, it is considered that $\mu = 80.194 \mathrm{MPa}$ and $\kappa = 120.291 \mathrm{MPa}$. Also, $\mu = 80.194 \mathrm{MPa } \mathrm{MPa}$ is selected in the case of incompressible membrane. The convergence behavior of developed approach can be analyzed in Fig. 7 in which the vertical displacement of point A of membrane is plotted versus the number of nodes for various values of shearing force. The results are generated for both compressible and incompressible cases. Moreover, for the compressible structure, the present results are compared to those reported in [28]. The converging trend as well as validity of approach can be clearly seen from the figure. Besides, Fig. 8 shows the deformed configurations of compressible Cook’s membrane for various values of nodes.

Fig. 6

Schematic of Cook’s membrane example

Fig. 7

Variation of vertical displacement of point ${\varvec{A}}$ of Cook's membrane in the compressible and incompressible regimes with the number of nodes for various values of shearing force(${n}_{2}=5, \left[\kappa ,\mu \right] = \left[\mathrm{120.291,80.194}\right] \, {\text{MPa}}$ for compressible, $\mu =80.194MPa$ for incompressible)

Fig. 8

Deformed configuration of the of Cook’s membrane under shearing force in the compressible regime (f $=24\,{\text{N/m{m}}}^{2}, \left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]\,{\text{MPa}}$)

3.4 Ring plate

As the fourth example, a ring plate under distributed load is considered whose geometrical properties and loading condition can be observed in Fig. 9. Two cases are considered:

Fig. 9

Schematic of ring plate example

• a) Thin ring plate with the following properties:

  $t=0.03\,{\text{mm}}$, $\mu = 10.5e6\, {\mathrm{MPa}} ;\, \kappa = 7e6\, \mathrm{MPa}$ for compressible regime.

  Figure 10 is given for testing the convergence and validation. In this figure, the vertical displacement of point ${\varvec{A}}$ of thin ring plate is plotted versus the number of nodes for various values of distributed force. A comparison is also provided with the results reported in [34].

• b) Thick ring plate with the following properties:

  $t=1\, {\text{mm}}$, $\mu = 80.194\, {\mathrm{MPa}} ;\, \kappa = 120.291\, \mathrm{MPa}$ for compressible regime.

  $\mu = 80.194$ for incompressible regime.

Figure 11 represents the variation of vertical displacement of ${\varvec{A}}$ and ${\varvec{B}}$ points of a thick ring plate under distributed load in both compressible and incompressible regimes. In addition, the deformed configurations are illustrated in Fig. 12.

Fig. 10

Variation of vertical displacement of point ${\varvec{A}}$ of thin ring plate with the number of nodes for various values of distributed force (${n}_{1}={n}_{3}=5, t=0.03\, {\text{mm}}, \left[\kappa ,\mu \right] = \left[\mathrm{7,10.5}\right]\times {10}^{6}\,{\text{MPa}}$)

Fig. 11

Variation of vertical displacement of ${\varvec{A}}$ and ${\varvec{B}}$ points of a thick ring plate under distributed load in compressible and incompressible regimes ($t=1 {\text{mm}}, \left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]\,{\text{MPa}}$ for compressible, $\mu =80.194\,{\text{MPa}}$ for incompressible)

Fig. 12

Deformed configurations of the thick ring plate under distributed load f($t=1\,{\text{mm}}, \left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]\,{\text{MPa}}$)

3.5 Cylindrical shell

In this example, as shown in Fig. 13, a thick cylindrical shell under uniform load is considered. The material properties are chosen as follows.

Fig. 13

Schematic of cylindrical shell example

$\mu = 6000\, \mathrm{MPa} ; \kappa = 24000\, \mathrm{MPa}$ for compressible regime.

$\mu = 6000\, \mathrm{MPa}$ for incompressible regime.

In Fig. 14, the displacement of point ${\varvec{A}}$ is plotted against the applied force for both compressible and incompressible cases. ${\varvec{A}}$ comparison is also made with the results of [33]. It is seen that the introduced approach is able to compute the large deformations of thick hyperelastic cylindrical shells. Deformed configurations of compressible shell are also illustrated in Fig. 15 for three values of applied force magnitude.

Fig. 14

Variation of displacement of point ${\varvec{A}}$ of a cylindrical shell under uniform load in the compressible and incompressible regimes ($\left[\kappa ,\mu \right] = \left[\mathrm{24000,6000}\right]\, {\text{MPa}}$ for compressible, $\mu =6000MPa$ for incompressible)

Fig. 15

Deformed configurations of the cylindrical shell under uniform load in the compressible regime ($\left[\kappa ,\mu \right] = \left[\mathrm{24000,6000}\right]\, {\text{MPa}}$)

3.6 Spherical shell

As indicated in Fig. 16, a hemispherical shell subjected to concentrated load is considered. Material properties of this example are.

Fig. 16

Schematic of spherical shell example

$\mu = 80.194\, \mathrm{MPa} ; \kappa = 120.291\, \mathrm{MPa}$ for compressible regime.

$\mu = 80.194\, \mathrm{MPa}$ for incompressible regime.

Figure 17 shows the variation of displacement of points ${\varvec{A}}$ and ${\varvec{B}}$ with the applied force for the compressible and incompressible regimes. Finally, the deformed configurations of compressible shell for three values of applied force are represented in Fig. 18.

Fig. 17

Variation of displacement of points ${\varvec{A}}$ and ${\varvec{B}}$ of hemispherical shell under concentrated load in the compressible and incompressible regimes ($\left[\kappa ,\mu \right] = \left[\mathrm{120.291,80.19}4\right]\, \mathrm{MPa}$ for compressible, $\mu =80.194MPa$ for incompressible)

Fig. 18

Deformed configurations of the hemispherical shell under concentrated load in the compressible regime($\left[\kappa ,\mu \right]=\left[\mathrm{120.291,80.194}\right]\, \mathrm{MPa}$)

4 Conclusion

Using the VDQ technique together with the idea of position transformation, and based on the 3D nonlinear elasticity, a numerical approach was proposed in this article for studying the large deformations of hyperelastic solids with arbitrary shapes under various loading conditions. The analysis was performed for both compressible and incompressible regimes. The governing equations were obtained using the minimum total potential energy principle considering the Neo-Hookean model. One of the main novelties of the work is related to its formulation which was presented in compact vector–matrix form and useful in the programming. Another important novelty was that the irregular domain of elements is transformed into a regular one by the method of mapping of position field based on the finite element shape functions in implementing the VDQ method. This feature enabled the proposed VDQ-transformed approach to solve problems with irregular domains. Some problems were solved to show the performance of the approach in both compressible and incompressible regimes. Simple implementation due to its compact matricized formulation, high accuracy, good convergence and applicability for various geometries can be mentioned as the advantages of developed VDQ-transformed approach.

Appendices

Appendix

Deformation Jacobian

Here, the deformation Jacobian and its derivatives, which are fundamental parameters in calculating the stress and elasticity modulus, are formulated. To this end, the vector–matrix and discretized representations of following relations are obtained

$$ \begin{aligned} J = \det \left( {\mathbf{F}} \right) & = F_{11} \left( {F_{22} F_{33} - F_{23} F_{32} } \right) - F_{12} \left( {F_{21} F_{33} - F_{23} F_{31} } \right) \\ & \quad + F_{13} \left( {F_{21} F_{32} - F_{22} F_{31} } \right) \\ \end{aligned} $$

(A1)

$$ J_{{,{\mathbf{F}}}} = \frac{\partial J}{{\partial {\mathbf{F}}}} = J{\mathbf{F}}^{{ - {\text{T}}}} $$

(A2)

$$ J_{{,{\mathbf{FF}}}} = \frac{{\partial J_{{,{\mathbf{F}}}} }}{{\partial {\mathbf{F}}}} = J{\mathbf{F}}^{{ - {\text{T}}}} \otimes {\mathbf{F}}^{{ - {\text{T}}}} - J{\mathbf{F}}^{ - 1} \underline { \otimes } {\mathbf{F}}^{{ - {\text{T}}}} $$

(A3)

2.1 Vector–matrix form

$$ J = \hat{F}_{1} \left( {\hat{F}_{5} \hat{F}_{9} - \hat{F}_{8} \hat{F}_{6} } \right) - \hat{F}_{4} \left( {\hat{F}_{2} \hat{F}_{9} - \hat{F}_{8} \hat{F}_{3} } \right) + \hat{F}_{7} \left( {\hat{F}_{2} \hat{F}_{6} - \hat{F}_{5} \hat{F}_{3} } \right) = {\hat{\mathbf{F}}}^{{\text{T}}} {\mathbf{G}}\hat{\mathbf{F}} $$

(A4)

$$ J_{{,{\hat{\mathbf{F}}}}} = \lceil J_{{,{\mathbf{F}}}}\rceil_{2} = \frac{\partial J}{{\partial {\hat{\mathbf{F}}}}} = \left( {\mathbf{G}} + {\mathbf{G}}^{\rm{T}} + \left( {\mathbf{I}}_{9} \circledast {\hat{\mathbf{F}}}^{\rm{T}}\right){\mathbf{H}}_{1}\right){\hat{\mathbf{F}}} $$

(A5)

$${J}_{,\widehat{\mathbf{F}}\widehat{\mathbf{F}}}={\lceil{J}_{,\mathbf{F}\mathbf{F}}\rceil}_{2}=\frac{\partial {J}_{,\widehat{\mathbf{F}}}}{\partial \widehat{\mathbf{F}}}=\left({\mathbf{H}}_{2} + {\mathbf{H}}_{1}^{\rm{T}}\right) \left({\mathbf{I}}_{9}\circledast\widehat{\mathbf{F}}\right)+\left({\mathbf{I}}_{9}\circledast{\widehat{\mathbf{F}}}^{\mathrm{T}}\right) {\mathbf{H}}_{1}+{\acute{\acute{{\mathbf{I}}}}}\left({\mathbf{I}}_{9}\circledast {\mathbf{H}}_{1}\widehat{\mathbf{F}}\right)$$

(A6)

in which

$$\mathbf{G}={\mathbf{T}}_{1}^{\mathrm{T}}\left({\mathbf{I}}_{3}\circledast{\widehat{\mathbf{F}}}^{\mathrm{T}}\right){\mathbf{T}}_{5},$$

(A7)

$${\mathbf{H}}_{1}={\lceil\frac{\partial \mathbf{G}}{\partial \widehat{\mathbf{F}}}\rceil}_{2}=\left[\begin{array}{c}{\mathbf{G}}_{,{\widehat{F}}_{1}}\\ {\mathbf{G}}_{,{\widehat{F}}_{2}}\\ \vdots \\ {\mathbf{G}}_{,{\widehat{F}}_{9}}\end{array}\right]=\left({\mathbf{I}}_{9}\circledast{\mathbf{T}}_{1}^{\mathrm{T}}\right)\acute{\mathbf{I}}{\mathbf{T}}_{5},$$

(A8)

$${\mathbf{H}}_{2}=\left[\begin{array}{cccc}{\mathbf{G}}_{,{\widehat{F}}_{1}}& {\mathbf{G}}_{,{\widehat{F}}_{2}}& \cdots & {\mathbf{G}}_{,{\widehat{F}}_{9}}\end{array}\right],$$

(A9)

$${\mathbf{T}}_{0}=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& -1& 0\\ 0& -1& 0& 0\\ 1& 0& 0& 0\end{array}\right], {\mathbf{T}}_{1}=\left[\begin{array}{c}{{\mathbf{I}}_{9}}_{1:}\\ -{{\mathbf{I}}_{9}}_{4:}\\ {{\mathbf{I}}_{9}}_{7:}\end{array}\right]$$

(A10)

$${\mathbf{T}}_{2}={\mathbf{B}}_{2}^{\mathrm{T}}{\mathbf{T}}_{0}{\mathbf{B}}_{2}/2, {\mathbf{T}}_{3}={\mathbf{B}}_{3}^{\mathrm{T}}{\mathbf{T}}_{0}{\mathbf{B}}_{3}/2, {\mathbf{T}}_{4}={\mathbf{B}}_{4}^{\mathrm{T}}{\mathbf{T}}_{0}{\mathbf{B}}_{4}/2, {\mathbf{T}}_{5}=\left[\begin{array}{c}{\mathbf{T}}_{2}\\ {\mathbf{T}}_{3}\\ {\mathbf{T}}_{4}\end{array}\right]$$

(A11)

$${{\mathbf{B}}_{2}={{\mathbf{I}}_{9}}_{\left\{\mathrm{5,6},\mathrm{8,9}\right\}:},\mathbf{B}}_{3}={{\mathbf{I}}_{9}}_{\left\{\mathrm{2,3},\mathrm{8,9}\right\}:},{\mathbf{B}}_{4}={{\mathbf{I}}_{9}}_{\left\{\mathrm{2,3},\mathrm{5,6}\right\}:}$$

(A12)

$$\acute{\mathbf{I}}=\left[\begin{array}{c}{\mathbf{I}}_{3}\circledast{{\mathbf{I}}_{9}}_{1:}\\ \vdots \\ {\mathbf{I}}_{3}\circledast{{\mathbf{I}}_{9}}_{9:}\end{array}\right], \acute{\acute{\mathbf{I}}}=\left[\begin{array}{ccc}\left({\mathbf{I}}_{9}\circledast{{\mathbf{I}}_{9}}_{1:}\right)& \cdots & \left({\mathbf{I}}_{9}\circledast{{\mathbf{I}}_{9}}_{9:}\right)\end{array}\right],$$

(A13)

$${\mathbf{I}}_{\left\{\blacksquare\right\}:}=\mathbf{I}\left(\left\{\blacksquare\right\},:\right),\boldsymbol{ }{\mathbf{I}}_{:\left\{\blacksquare\right\}}=\mathbf{I}\left(:,\left\{\blacksquare\right\}\right)$$

(A14)

2.2 Discretized form

$${\mathbb{J}}={\left[\kern-0.15em\left[J\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}={\mathop{\widehat{\mathbb{F}}}\limits^{\smile}}^{\mathrm{T}}\mathop{{\mathbb{G}}}\limits^{\smile}\widehat{\mathbb{F}}$$

(A15)

$${\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}}}\limits^{\smile}}={\left[\kern-0.15em\left[{J}_{,\widehat{\mathbf{F}}}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}=\left({\mathop{{\mathbb{G}}}\limits^{\smile}}+{{\mathop{{\mathbb{G}}}\limits^{\smile}}}^{\mathrm{T}}+\left({\mathbf{I}}_{9}\circledast{\mathop{\widehat{\mathbb{F}}}\limits^{\smile}}^{\mathrm{T}}\right){\mathop{{\mathbb{H}}}\limits^{\smile}}_{1}\right)\widehat{\mathbb{F}}$$

(A16)

$${\mathop{{\mathbb{J}}_{,\hat{\mathbb{F}}\hat{\mathbb{F}}}}\limits^{\smile}}={\langle {\left[\kern-0.15em\left[{J}_{,\widehat{\mathbf{F}} \widehat{\mathbf{F}}}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}} \rangle }_{\mathbb{b}}=\left({\mathop{{\mathbb{G}}} \limits^{\smile}}+{{\mathop{{\mathbb{G}}}\limits^{\smile\mathrm{T}}}}\right)+\left({\mathop{{\mathbb{H}}} \limits^{\smile}}_{2} + {\mathop{{\mathbb{H}}} \limits^{\smile}}_{1}^{\rm{T}}\right)\left({\mathbf{I}}_{9}\circledast{\mathop{{\widehat{\mathbb{F}}}}\limits^{\smile}}\right)+\left({\mathbf{I}}_{9}\circledast{\mathop{\widehat{\mathbb{F}}}\limits^{\smile\mathrm{T}}}\right){\mathop{{\mathbb{H}}} \limits^{\smile}}_{1}+{\mathop{{\acute{\acute{{\mathbf{I}}}}}}\limits^{\smile}}\left({\mathbf{I}}_{9}\circledast {\mathop{{\mathbb{H}}} \limits^{\smile}}_{1}\mathop{{\widehat{\mathbb{F}}}}\limits^{\smile}\right),$$

(A17)

where

$${\mathop{{\mathbb{G}}}\limits^{\smile}}={\langle {\left[\kern-0.15em\left[\mathbf{G}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}=\left({\mathbf{T}}_{1}^{\mathrm{T}}\circledast{\mathop{\widehat{\mathbb{F}}}\limits^{\smile}}^{\mathrm{T}}\right)\left({\mathbf{T}}_{5}\circledast{\mathbf{I}}_{n}\right)$$

(A18)

$${\mathop{{\mathbb{H}}} \limits^{\smile}}_{1}={\langle {\left[\kern-0.15em\left[{\mathbf{H}}_{1}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}={\mathbf{H}}_{1}\circledast{\mathbf{I}}_{n}, {\mathop{{\mathbb{H}}} \limits^{\smile}}_{2} ={\langle {\left[\kern-0.15em\left[{\mathbf{H}}_{2}\right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}={\mathbf{H}}_{2}\circledast{\mathbf{I}}_{n} $$

(A19)

$$\breve{\acute{\mathbb{I}}}={\langle { \left[\kern-0.15em\left[ {\acute{\mathbf{I}}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}={\acute{\mathbf{I}}}\circledast{\mathbf{I}}_{n},{\breve{\acute{\acute{\mathbb{I}}}}}={\langle { \left[\kern-0.15em\left[ \acute{\acute{\mathbb{I}}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}=\acute{\acute{\mathbf{I}}}\circledast{\mathbf{I}}_{n},\breve{\mathbb{I}}_{9}={\langle { \left[\kern-0.15em\left[ {{\mathbf{I}}_{9}} \right]\kern-0.15em\right]}_{{\mathfrak{C}}_{0}}\rangle }_{\mathbb{b}}={\mathbf{I}}_{9}\circledast{\mathbf{I}}_{n}$$

(A20)

Details of the VDQ-based approach

Here, the numerical differential and integral operators of VDQ method are first obtained in the natural space; then, they are transformed to the numerical operators of Cartesian space using 3D shape functions. Based on the mentioned mapping technique, the VDQ method becomes able to study irregular domains.

3.1 Numerical VDQ-operators

3.1.1 Definition of derivative operator

$${\left[\kern-0.15em\left[{f}_{,{\blacksquare}_{1}}\right]\kern-0.15em\right]}_{{\blacksquare}_{2}}={\stackrel{{\blacksquare}_{3}}{\varvec{\mathcal{D}}}}_{{\blacksquare}_{1};{\blacksquare}_{2}}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\blacksquare}_{2}}={\stackrel{{\blacksquare}_{3}}{\varvec{\mathcal{D}}}}_{{\blacksquare}_{1};{\blacksquare}_{2}}{\mathbb{f}},$$

(B1)

where.

${\blacksquare}_{1}:$ Variable with respect to which derivative is taken.

${\blacksquare}_{2}$: Domain on which differentiation is performed.

${\blacksquare}_{3}$: Dimension of problem ($1d,2d,3d$).

3.1.2 Definition of integral operator

$${\int }_{{\blacksquare}_{2}}fd{\blacksquare}_{1}={\stackrel{{\blacksquare}_{3}}{\varvec{\mathcal{S}}}}_{{\blacksquare}_{1};{\blacksquare}_{2}}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\blacksquare}_{2}}={\stackrel{{\blacksquare}_{3}}{\varvec{\mathcal{S}}}}_{{\blacksquare}_{1};{\blacksquare}_{2}}{\mathbb{f}} ,$$

(B2)

where.

${\blacksquare}_{1}:$ Variable with respect to which integral is taken.

${\blacksquare}_{2}:$ Domain on which integration is performed.

${\blacksquare}_{3}$: Dimension of problem ($1d,2d,3d$).

3.1.3 Definition of discretization operator

The 3D discretization of scalar $f$ on the volume $V$ in ${s}_{1}-{s}_{2}-{s}_{3}$ direction, respectively, can be expressed as

$${\mathbb{f}}={\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{V}= \left[{\mathbf{f}}_{;1}\quad{\mathbf{f}}_{;2}\quad\cdots\quad{\mathbf{f}}_{;n_1}\quad\cdots\quad{\mathbf{f}}_{;{n_1}{n_2}{n_3}}\right],$$

(B3)

Moreover, the 3D discretization of matrix $\mathbf{f}$ on the volume $V$ in ${s}_{1}-{s}_{2}-{s}_{3}$ direction is given by

$${\mathbb{f}}={\left[\kern-0.15em\left[\mathbf{f}\right]\kern-0.15em\right]}_{V}=\left[\begin{array}{ccc}{\left[\kern-0.15em\left[{f}_{11}\right]\kern-0.15em\right]}_{V}& \cdots & {\left[\kern-0.15em\left[{f}_{1r}\right]\kern-0.15em\right]}_{V}\\ \vdots & \ddots & \vdots \\ {\left[\kern-0.15em\left[{f}_{r1}\right]\kern-0.15em\right]}_{V}& \cdots & {\left[\kern-0.15em\left[{f}_{rs}\right]\kern-0.15em\right]}_{V}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{f}}_{\mathbf{11}}& \cdots & {\mathbf{f}}_{{\mathbf{1}}{\varvec{R}}}\\ \vdots & \ddots & \vdots \\ {\mathbf{f}}_{{\varvec{R}}{\mathbf{1}}}& \cdots & {\mathbf{f}}_{{\varvec{R}}{\varvec{S}}}\end{array}\right], {\mathbf{f}}_{\mathbf{IJ}} = {\left[\kern-0.15em\left[{f_{ij}}\right]\kern-0.15em\right]}_{V} = \left[\begin{array}{ccc}{\mathbf{f}}_{{\varvec{IJ}};1} \\ {\mathbf{f}}_{{\varvec{IJ}};2}\\ \vdots \\{\mathbf{f}}_{{\varvec{IJ}};n1n2n3}\end{array}\right]$$

(B4)

3.1.4 Computational points

The discretization is performed based on Chebyshev distribution in the natural space:

${{\varvec{\upzeta}}}^{cheb}=$ Chebyshev-distribution ($\mathrm{domain},\mathrm{node number})$ (B5).

For the 3D case one can write

$${{\varvec{\upxi}}}_{1}=\left[\begin{array}{cccc}{{\varvec{\upxi}}}_{1;1}& {{\varvec{\upxi}}}_{1;2}& \cdots &{{\varvec{\upxi}}}_{1;n}\end{array}\right]={\left[\kern-0.15em\left[{\xi }_{1}\right]\kern-0.15em\right]}_{V}={\varvec{1}}_{{n}_{3}*1}\circledast {\varvec{1}}_{{n}_{2}*1}\circledast {{\varvec{\upzeta}}}_{1}^{cheb},$$

$${{\varvec{\upxi}}}_{2}=\left[\begin{array}{cccc}{{\varvec{\upxi}}}_{2;1}& {{\varvec{\upxi}}}_{2;2}& \cdots & {{\varvec{\upxi}}}_{2;n}\end{array}\right]={\left[\kern-0.15em\left[{\xi }_{2}\right]\kern-0.15em\right]}_{V}={{\varvec{1}}_{{n}_{3}*1}}\circledast {{{\varvec{\upzeta}}}_{2}^{cheb}}\circledast {\varvec{1}}_{{n}_{1}*1},$$

$${{\varvec{\upxi}}}_{3}=\left[\begin{array}{cccc}{{\varvec{\upxi}}}_{3;1}& {{\varvec{\upxi}}}_{3;2}& \cdots & {{\varvec{\upxi}}}_{3;n}\end{array}\right]={\left[\kern-0.15em\left[{\xi }_{3}\right]\kern-0.15em\right]}_{V}={{\varvec{\upzeta}}}_{1}^{cheb}\circledast{\varvec{1}}_{{n}_{2}*1}\circledast{\varvec{1}}_{{n}_{1}*1},$$

$${\bar{\bar{{\varvec{\upxi}}}}}={\left[\kern-0.15em\left[\left[\begin{array}{c}{\xi }_{1}\\ {\xi }_{2}\\ {\xi }_{3}\end{array}\right]\right]\kern-0.15em\right]}_{V}=\left[\begin{array}{c}{{\varvec{\upxi}}}_{\varvec{1}}\\ {{\varvec{\upxi}}}_{\varvec{2}}\\ {{\varvec{\upxi}}}_{\varvec{3}}\end{array}\right],$$

(B6)

where

${{\varvec{\upzeta}}}_{1}^{cheb}=$ Chebyshev-distribution ($\left[-\mathrm{1,1}\right],{n}_{1})$

${{\varvec{\upzeta}}}_{2}^{cheb}=$ Chebyshev-distribution ($\left[-\mathrm{1,1}\right],{n}_{2})$

${{\varvec{\upzeta}}}_{3}^{cheb}=$ Chebyshev-distribution ($\left[-\mathrm{1,1}\right],{n}_{3})$

3.1.5 Computation of derivative operator in natural space

The 1d derivative operator in the natural space is defined as follows

$${\mathbb{f}}_{,\bar{\bar{\xi }}}^{\left(r\right)}={\left[\kern-0.15em\left[{f}_{,\xi }^{\left(r\right)}\right]\kern-0.15em\right]}_{{\check{\varGamma}}}={\stackrel{1d}{\varvec{\mathcal{D}}}}_{\xi }^{\left(r\right)}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{\varGamma}}}={\stackrel{1d}{\varvec{\mathcal{D}}}}_{\xi }^{\left(r\right)}{\mathbb{f}},$$

(B7)

$${D}_{\xi ij}^{\left(r\right)}=\left\{\begin{array}{lll}{\delta }_{ij}& &r=0,\\ \frac{{P_i}}{\left({{\varvec{\upxi}}}_{;i}-{{\varvec{\upxi}}}_{;j}\right){P}_{j}}&i\ne j,&r=1,\\ r\left({D}_{\xi ij}^{\left(1\right)}{D}_{\xi ii}^{\left(r-1\right)}-\frac{{D}_{\xi ij}^{\left(r-1\right)}}{\left({{\varvec{\upxi}}}_{;i}-{{\varvec{\upxi}}}_{;j}\right)}\right)&i\ne j,&r=\mathrm{2,3},\dots ,n-1,\\ - \sum\limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne 1} \\ \end{array} }}^{n} {D_{{\xi ij}}^{{\left( r \right)}} } &i=j,&r=\mathrm{1,2},3,\dots ,n-1,\end{array},\right.$$

(B8)

in which

$${P}_{j}=\prod_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left({{\varvec{\upxi}}}_{;j}-{{\varvec{\upxi}}}_{;i}\right),$$

(B9)

Furthermore, ${{\varvec{\upxi}}}_{;i}$ is ith element of $\overline{\overline{\xi }}$. Finally.

$${\stackrel{1d}{\varvec{\mathcal{D}}}}_{\xi }^{(r)}={\stackrel{1d}{\varvec{\mathcal{D}}}}_{,\underset{r}{\underbrace{\xi \dots \xi }}}=\left[{D}_{\xi ij}^{\left(r\right)}\right],$$

(B10)

Similarly, the 3d derivative operator is constructed as

$${\mathbb{f}}_{,{{\varvec{\upxi}}}_{1}}^{(r)}={\left[\kern-0.15em\left[{f}_{,{\xi }_{1}}^{(r)}\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{1}}^{(r)}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{1}}^{(r)}{\mathbb{f}}, {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{1}}^{(r)}={\mathbf{I}}_{{n}_{3}}\circledast{\mathbf{I}}_{{n}_{2}}\circledast{\stackrel{1d}{\varvec{\mathcal{D}}}}_{{\xi }_{1}}^{\left(r\right)},$$

(B11)

$${\mathbb{f}}_{,{{\varvec{\upxi}}}_{2}}^{(r)}={\left[\kern-0.15em\left[{f}_{,{\xi }_{2}}^{(r)}\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{2}}^{(r)}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\mathcal{D}}}_{{\xi }_{2}}^{\left(r\right)}{\mathbb{f}}, {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{2}}^{\left(r\right)}={\mathbf{I}}_{{n}_{3}}\circledast{\stackrel{1d}{\varvec{\mathcal{D}}}}_{{\xi }_{2}}^{\left(r\right)}\circledast{\mathbf{I}}_{{n}_{1}},$$

(B12)

$${\mathbb{f}}_{,{{\varvec{\upxi}}}_{3}}^{(r)}={\left[\kern-0.15em\left[{f}_{,{\xi }_{3}}^{(r)}\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{3}}^{(r)}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{3}}^{\left(r\right)}{\mathbb{f}}, {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{3}}^{\left(r\right)}={\stackrel{1d}{\varvec{\mathcal{D}}}}_{{\xi }_{3}}^{\left(r\right)}\circledast{\mathbf{I}}_{{n}_{2}}\circledast{\mathbf{I}}_{{n}_{1}},$$

(B13)

$${\mathbb{f}}_{\bar{\bar{{\varvec{\upxi}}}}}^{(r)}={\left[\kern-0.15em\left[{f}_{,{\varvec{\upxi}}}^{(r)}\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\varvec{\upxi}}}^{(r)}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\varvec{\upxi}}}^{(r)}{\mathbb{f}},{\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\varvec{\upxi}}}^{(r)}=\left[\begin{array}{c}{\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{1}}^{(r)}\\ {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{2}}^{\left(r\right)}\\ {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{3}}^{\left(r\right)}\end{array}\right]$$

(B14)

3.1.6 Computation of integral operator in natural space

The discretized form of $1d$ integral operator in natural space is introduced as

$$I={\int }_{\check{\varGamma}}f\left(\xi \right)d\xi ={\stackrel{1d}{\varvec{\mathcal{S}}}}_{\xi }{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{\check{\varGamma}}={\stackrel{1d}{\varvec{\mathcal{S}}}}_{\xi }{\mathbb{f}},$$

(B15)

$${\stackrel{1d}{\varvec{\mathcal{S}}}}_{\xi }=\sum_{r=0}^{\infty }{\mathbf{K}}_{tay}^{\left(r\right)}{\stackrel{1d}{\varvec{\mathcal{D}}}}_{\xi }^{\left(r\right)},$$

(B16)

$${\mathbf{K}}_{tay}^{\left(r\right)}=\left[\frac{{\left({{\varvec{\upxi}}}_{;2}-{{\varvec{\upxi}}}_{;1}\right)}^{r+1}}{{2}^{r+1}\left(r+1\right)!} \dots \frac{{\left({{\varvec{\upxi}}}_{;i+1}-{{\varvec{\upxi}}}_{;i}\right)}^{r+1}-{\left({{\varvec{\upxi}}}_{;i-1}-{{\varvec{\upxi}}}_{;i}\right)}^{r+1}}{{2}^{r+1}\left(r+1\right)!} \dots \frac{{\left({{\varvec{\upxi}}}_{;n-1}-{{\varvec{\upxi}}}_{;n}\right)}^{r+1}}{{2}^{r+1}\left(r+1\right)!}\right],$$

(B17)

where ${{\varvec{\upxi}}}_{;i}$ denotes ith element of $\overline{\overline{\xi }}$.

For the 3D operator one has

$$\mathrm{I}={\int }_{{\check{V}}}f d{\xi }_{1}d{\xi }_{2}d{\xi }_{3}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{\varvec{\upxi}}}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{{\check{V}}}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{\varvec{\upxi}}}{\mathbb{f}},$$

(B18)

$${\stackrel{3d}{\varvec{\mathcal{S}}}}_{{\varvec{\upxi}}}={\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{3}}\circledast{\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{2}}\circledast{\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{1}},$$

(B19)

in which ${\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{1}}$, ${\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{2}}$ and ${\stackrel{1d}{\varvec{\mathcal{S}}}}_{{\xi }_{3}}$ are evaluated based on Eq. (B16).

3.2 FE-Transformation:

The following relations are given for the mapping procedure of physical arbitrary shape domain into regular computational one.

3.2.1 Shape functions

$${\mathbf{N}}_{X}={\left[\begin{array}{cccc}{{N}_{X}}_{1}& {{N}_{X}}_{2}& \cdots & {{N}_{X}}_{{n}_{tp}}\end{array}\right]}^{\mathrm{T}},$$

(B20)

3.2.1.1 Discretized form

$${\mathbb{N}}_{X}={\left[\kern-0.15em\left[{\mathbf{N}}_{X}\right]\kern-0.15em\right]}_{V}=\left[\begin{array}{c}{{\mathbf{N}}_{X}}_{\varvec{1}}\\ {{\mathbf{N}}_{X}}_{\varvec{2}}\\ \vdots \\ {{\mathbf{N}}_{X}}_{{{\varvec{n}}}_{{\varvec{tp}}}}\end{array}\right],{{\mathbf{N}}_{X}}_{{\varvec{I}}}={\left[\kern-0.15em\left[{{N}_{X}}_{i}\right]\kern-0.15em\right]}_{V},$$

(B21)

3.2.2 Position field

3.2.2.1 Vector–matrix form

$$\left\{\begin{array}{c}{X}_{\varvec{1}}\left({\varvec{\upxi}}\right)=\sum_{m=1}^{{n}_{tp}}{N}_{X m}{\mathbf{X}}_{{\varvec{1}};m}^{tp}=\left[\begin{array}{ccc}{{N}_{X}}_{{1}}& \cdots & {{N}_{X}}_{{n}_{tp}}\end{array}\right]\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{1}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{1}};{n}_{tp}}^{tp}\end{array}\right]={\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{1}}^{tp}\\ {X}_{\varvec{2}}\left({\varvec{\upxi}}\right)=\sum_{m=1}^{{n}_{tp}}{N}_{X m}{\mathbf{X}}_{{\varvec{2}};m}^{tp}=\left[\begin{array}{ccc}{{N}_{X}}_{{1}}& \cdots & {{N}_{X}}_{{n}_{tp}}\end{array}\right]\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{2}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{2}};{n}_{tp}}^{tp}\end{array}\right]={\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{2}}^{tp}\\ {X}_{\varvec{3}}\left({\varvec{\upxi}}\right)=\sum_{m=1}^{{n}_{tp}}{N}_{X m}{\mathbf{X}}_{{\varvec{3}};m}^{tp}=\left[\begin{array}{ccc}{{N}_{X}}_{{1}}& \cdots & {{N}_{X}}_{{n}_{tp}}\end{array}\right]\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{3}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{3}};{n}_{tp}}^{tp}\end{array}\right]={\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{3}}^{tp}\end{array}\right.$$

(B22)

$$\mathbf{X}\left({\varvec{\upxi}}\right)=\left[\begin{array}{c}{X}_{1}\\ {X}_{2}\\ {X}_{3}\end{array}\right]=\left[\begin{array}{c}{\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{1}}^{tp}\\ {\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{2}}^{tp}\\ {\mathbf{N}}_{X}^{\mathrm{T}}{\mathbf{X}}_{\varvec{3}}^{tp}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{N}}_{X}^{\mathrm{T}}& 0& 0\\ 0& {\mathbf{N}}_{X}^{\mathrm{T}}& 0\\ 0& 0& {\mathbf{N}}_{X}^{\mathrm{T}}\end{array}\right]\left[\begin{array}{c}{\mathbf{X}}_{\varvec{1}}^{tp}\\ {\mathbf{X}}_{\varvec{2}}^{tp}\\ {\mathbf{X}}_{\varvec{3}}^{tp}\end{array}\right]=\left({\mathbf{I}}_{3}\circledast{\mathbf{N}}_{X}^{\mathrm{T}}\right)\left[\begin{array}{c}{\mathbf{X}}_{\varvec{1}}^{tp}\\ {\mathbf{X}}_{\varvec{2}}^{tp}\\ {\mathbf{X}}_{\varvec{3}}^{tp}\end{array}\right]={\mathbf{N}}_{X}^{\mathbf{*}}{\mathbb{X}}^{tp}$$

(B23)

where

$${\mathbf{N}}_{X}^{\mathbf{*}}=\left({\mathbf{I}}_{3}\circledast{\mathbf{N}}_{X}^{\mathrm{T}}\right),\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{\mathbf{N}}_{X}={\left[\begin{array}{ccc}{{N}_{X}}_{1}& \cdots & {{N}_{X}}_{{n}_{tp}}\end{array}\right]}^{\mathrm{T}}$$

(B24)

$${\mathbb{X}}^{tp}=\left[\begin{array}{c}{\mathbf{X}}_{\varvec{1}}^{tp}\\ {\mathbf{X}}_{\varvec{2}}^{tp}\\ {\mathbf{X}}_{\varvec{3}}^{tp}\end{array}\right],{\mathbf{X}}_{\varvec{1}}^{tp}=\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{1}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{1}};{n}_{tp}}^{tp}\end{array}\right], {\mathbf{X}}_{\varvec{2}}^{tp}=\left[\begin{array}{c}{\mathbf{X}}_{\varvec{{2}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{2}};{n}_{tp}}^{tp}\end{array}\right], {\mathbf{X}}_{\varvec{3}}^{tp}=\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{3}};1}^{tp}\\ \vdots \\ {\mathbf{X}}_{{\varvec{3}};{n}_{tp}}^{tp}\end{array}\right]$$

(B25)

where $\left[\begin{array}{c}{\mathbf{X}}_{{\varvec{1}};i}^{tp}\\ {\mathbf{X}}_{{\varvec{2}};i}^{tp}\\ {\mathbf{X}}_{{\varvec{3}};i}^{tp}\end{array}\right]$ is the Cartesian coordinate of ith transformation node.

3.2.2.2 Discretized form

$${\mathbb{X}}={\left[\kern-0.15em\left[\mathbf{X}\right]\kern-0.15em\right]}_{V}=\left[\begin{array}{c}{\mathbf{X}}_{\varvec{1}}\\ {\mathbf{X}}_{\varvec{2}}\\ {\mathbf{X}}_{\varvec{3}}\end{array}\right]={\mathbb{N}}_{X}^{\mathbf{*}}{\mathbb{X}}^{tp}$$

(B26)

$${\mathbb{N}}_{X}^{\mathbf{*}}={\left[\kern-0.15em\left[{\mathbf{N}}_{X}^{\mathbf{*}}\right]\kern-0.15em\right]}_{V}=\left({\mathbf{I}}_{3}\circledast\left[\begin{array}{cccc}{{\mathbf{N}}_{X}}_{\varvec{1}}& {{\mathbf{N}}_{X}}_{\varvec{2}}& \cdots & {{\mathbf{N}}_{X}}_{{{\varvec{n}}}_{{\varvec{t}}{\varvec{p}}}}\end{array}\right]\right)$$

(B27)

3.2.3 Computation of derivative operator in Cartesian space

3.2.3.1 Vector–matrix form

$${f}_{,{\varvec{\upxi}}}=\frac{\partial f}{\partial {X}_{j}}\frac{\partial {X}_{j}}{\partial {\xi }_{i}}{\mathbf{e}}_{i}={\mathbf{J}}^{tr}{f}_{,\mathbf{X}} \stackrel{ }{\Rightarrow } {f}_{,\mathbf{X}}=({{\mathbf{J}}^{tr})}^{-1}{f}_{,{\varvec{\upxi}}} $$

(B28)

$${\mathbf{J}}^{tr}=\left[\begin{array}{ccc}{J}_{11}^{tr}& {J}_{12}^{tr}& {J}_{13}^{tr}\\ {J}_{21}^{tr}& {J}_{21}^{tr}& {J}_{21}^{tr}\\ {J}_{31}^{tr}& {J}_{31}^{tr}& {J}_{31}^{tr}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial {X}_{1}}{\partial {\xi }_{1}}& \frac{\partial {X}_{2}}{\partial {\xi }_{1}}& \frac{\partial {X}_{3}}{\partial {\xi }_{1}}\\ \frac{\partial {X}_{1}}{\partial {\xi }_{2}}& \frac{\partial {X}_{2}}{\partial {\xi }_{2}}& \frac{\partial {X}_{3}}{\partial {\xi }_{2}}\\ \frac{\partial {X}_{1}}{\partial {\xi }_{3}}& \frac{\partial {X}_{2}}{\partial {\xi }_{3}}& \frac{\partial {X}_{3}}{\partial {\xi }_{3}}\end{array}\right]$$

(B29)

$${{\mathbf{J}}^{tr}}^{-1}=\frac{1}{{j}^{tr}}\left[\begin{array}{ccc}{J}_{22}^{tr}{J}_{33}^{tr}-{J}_{23}^{tr}{J}_{32}^{tr}& {J}_{13}^{tr}{J}_{32}^{tr}-{J}_{12}^{tr}{J}_{33}^{tr}& {J}_{12}^{tr}{J}_{23}^{tr}-{J}_{13}^{tr}{J}_{22}^{tr}\\ {J}_{23}^{tr}{J}_{31}^{tr}-{J}_{21}^{tr}{J}_{33}^{tr}& {J}_{11}^{tr}{J}_{33}^{tr}-{J}_{13}^{tr}{J}_{31}^{tr}& {J}_{13}^{tr}{J}_{21}^{tr}-{J}_{11}^{tr}{J}_{23}^{tr}\\ {J}_{21}^{tr}{J}_{32}^{tr}-{J}_{22}^{tr}{J}_{31}^{tr}& {J}_{12}^{tr}{J}_{31}^{tr}-{J}_{11}^{tr}{J}_{32}^{tr}& {J}_{11}^{tr}{J}_{22}^{tr}-{J}_{12}^{tr}{J}_{22}^{tr}\end{array}\right]$$

(B30)

where

$${j}^{tr}={j}_{11}^{tr}\left({j}_{22}^{tr}{j}_{33}^{tr}-{j}_{23}^{tr}{j}_{32}^{tr}\right)-{j}_{12}^{tr}\left({j}_{21}^{tr}{j}_{33}^{tr}-{j}_{23}^{tr}{j}_{31}^{tr}\right)+{j}_{13}^{tr}\left({j}_{21}^{tr}{j}_{32}^{tr}-{j}_{22}^{tr}{j}_{31}^{tr}\right)$$

3.2.3.2 Discretized form

$${\mathbb{f}}_{,{\mathbb{X}}}=\left[\begin{array}{c}{\mathbb{f}}_{,{\mathbf{X}}_{1}}\\ {\mathbb{f}}_{,{\mathbf{X}}_{2}}\\ {\mathbb{f}}_{,{\mathbf{X}}_{3}}\end{array}\right]={\left[\kern-0.15em\left[{f}_{,\mathbf{X}}\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{\mathbf{X}}{\mathbb{f}},\boldsymbol{ }\boldsymbol{ }\left\{\begin{array}{c}{\mathbb{f}}_{,{\mathbf{X}}_{1}}={\left[\kern-0.15em\left[{f}_{,{X}_{1}}\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{1}}f\\ {\mathbb{f}}_{,{\mathbf{X}}_{2}}={\left[\kern-0.15em\left[{f}_{,{X}_{2}}\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{2}}f\\ {\mathbb{f}}_{,{\mathbf{X}}_{3}}={\left[\kern-0.15em\left[{f}_{,{X}_{3}}\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{3}}f\end{array}\right.$$

(B31)

in which.

$${\stackrel{3d}{\varvec{\mathcal{D}}}}_{\mathbf{X}}=\left[\begin{array}{c}{\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{1}}\\ {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{2}}\\ {\stackrel{3d}{\varvec{\mathcal{D}}}}_{{X}_{3}}\end{array}\right]=\left({\mathbf{I}}_{3}\circledast\langle {\left({\mathbb{j}}^{tr}\right)}^{\circ -1}\rangle \right)\left[\begin{array}{ccc}{\mathbf{J}}_{22}^{tr}\circ {\mathbf{J}}_{33}^{tr}-{\mathbf{J}}_{23}^{tr}\circ {\mathbf{J}}_{32}^{tr}& {\mathbf{J}}_{13}^{tr}\circ {\mathbf{J}}_{32}^{tr}-{\mathbf{J}}_{12}^{tr}\circ {\mathbf{J}}_{33}^{tr}& {\mathbf{J}}_{12}^{tr}\circ {\mathbf{J}}_{23}^{tr}-{\mathbf{J}}_{13}^{tr}\circ {\mathbf{J}}_{22}^{tr}\\ {\mathbf{J}}_{23}^{tr}\circ {\mathbf{J}}_{31}^{tr}-{\mathbf{J}}_{21}^{tr}\circ {\mathbf{J}}_{33}^{tr}& {\mathbf{J}}_{11}^{tr}\circ {\mathbf{J}}_{33}^{tr}-{\mathbf{J}}_{13}^{tr}\circ {\mathbf{J}}_{31}^{tr}& {\mathbf{J}}_{13}^{tr}\circ {\mathbf{J}}_{21}^{tr}-{\mathbf{J}}_{11}^{tr}\circ {\mathbf{J}}_{23}^{tr}\\ {\mathbf{J}}_{21}^{tr}\circ {\mathbf{J}}_{32}^{tr}-{\mathbf{J}}_{22}^{tr}\circ {\mathbf{J}}_{31}^{tr}& {\mathbf{J}}_{12}^{tr}\circ {\mathbf{J}}_{31}^{tr}-{\mathbf{J}}_{11}^{tr}\circ {\mathbf{J}}_{32}^{tr}& {\mathbf{J}}_{11}^{tr}\circ {\mathbf{J}}_{22}^{tr}-{\mathbf{J}}_{12}^{tr}\circ {\mathbf{J}}_{22}^{tr}\end{array}\right]{\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\varvec{\upxi}}}$$

(B32)

$${\mathbb{j}}^{tr}={\left[\kern-0.15em\left[{j}^{tr}\right]\kern-0.15em\right]}_{V}$$

$$={\mathbf{J}}_{11}^{tr}\circ \left({\mathbf{J}}_{22}^{tr}\circ {\mathbf{J}}_{33}^{tr}-{\mathbf{J}}_{23}^{tr}\circ {\mathbf{J}}_{32}^{tr}\right)-{\mathbf{J}}_{12}^{tr}\circ \left({\mathbf{J}}_{21}^{tr}\circ {\mathbf{J}}_{33}^{tr}-{\mathbf{J}}_{23}^{tr}\circ {\mathbf{J}}_{31}^{tr}\right)+{\mathbf{J}}_{13}^{tr}\circ \left({\mathbf{J}}_{21}^{tr}\circ {\mathbf{J}}_{32}^{tr}-{\mathbf{J}}_{22}^{tr}\circ {\mathbf{J}}_{31}^{tr}\right)$$

(B33)

$${\mathbf{J}}_{{\varvec{I}}{\varvec{J}}}^{tr}={\left[\kern-0.15em\left[{J}_{ij}^{tr}\right]\kern-0.15em\right]}_{V}={\left[\kern-0.15em\left[\frac{\partial {X}_{j}}{\partial {\xi }_{i}}\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{D}}}}_{{\xi }_{i}}{\mathbf{X}}_{{\varvec{J}}}$$

(B34)

3.2.4 Computation of integral operator in Cartesian space

$$I={\int }_{V}fd{X}_{1}d{X}_{2}d{X}_{3}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3}}{\left[\kern-0.15em\left[f\right]\kern-0.15em\right]}_{V}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{X}_{1}{X}_{2}{X}_{3}}{\mathbb{f}},$$

(B35)

$${\stackrel{3d}{\varvec{\mathcal{S}}}}_{\mathbf{X}}={\stackrel{3d}{\varvec{\mathcal{S}}}}_{{\varvec{\upxi}}}\langle {\mathbb{j}}^{tr}\rangle $$

(B36)