Skip to main content
SpringerLink
Log in

On physical analysis of degree-based entropy measures for metal–organic superlattices

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

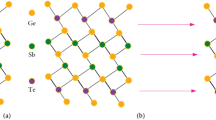
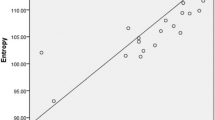
Two-dimensional materials have fascinated extensive attention due to their novel optical and mechanical properties for prospective applications. In (QSPR/QSAR) studies, the biological activity of underlying structure is associated with physical properties of structure by using topological indices. A huge spectrum of topological indices is available, among which the degree-based indices are used in this study. These indices have substantial iteration with the total \(\pi \)-electron energy. Moreover, we measure the graph entropies to obtain the structural information of two-dimensional trans-Pd–\(({\mathrm{NH}}_{2}){\mathrm{S}}\) lattice and a metal–organic superlattice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. D. Bonchev, Complexity in Chemistry, Introduction and Fundamentals (Taylor and Francis, Boca Raton, 2003)

    Book  Google Scholar 

  2. Z. Chen, M. Dehmer, Y. Shi, A note on distance based graph entropies. Entropy 16, 5416–5427 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  3. S. Cao, M. Dehmer, Y. Shi, Extremality of degree-based graph entropies. Inf. Sci. 278, 22–33 (2014)

    Article  MathSciNet  Google Scholar 

  4. C. Chakravarty, B. Mandal, P. Sarkar, Coronene-based metal–organic framework: a theoretical exploration. Phys. Chem. Chem. Phys. 18(36), 25277–25283 (2016)

    Article  Google Scholar 

  5. M. Dehmer, Information processing in complex networks: graph entropy and information functionals. Appl. Math. Comput. 201, 82–94 (2008)

    MathSciNet  MATH  Google Scholar 

  6. M. Dehmer, L. Sivakumar, K. Varmuza, Uniquely discriminating molecular structures using novel eigenvalue-based descriptors. MATCH Commun. Math. Comput. Chem. 67, 147–172 (2012)

    MathSciNet  Google Scholar 

  7. M. Dehmer, A. Mowshowitz, A history of graph entropy measures. Inf. Sci. 181, 57–78 (2011)

    Article  MathSciNet  Google Scholar 

  8. M. Dehmer, M. Graber, The discrimination power of molecular identification numbers revisited. MATCH Commun. Math. Comput. Chem. 69, 785–794 (2013)

    MATH  Google Scholar 

  9. W. Gao, M.K. Siddiqui, M. Naeem, N.A. Rehman, Topological characterization of carbon graphite and crystal cubic carbon structures. Molecules 22, 1496–1507 (2017)

    Article  Google Scholar 

  10. W. Gao, M.R. Farahani, Degree-based indices computation for special chemical molecular structures using edge dividing method. Appl. Math. Nonlinear Sci. 1(1), 94–117 (2015)

    MathSciNet  Google Scholar 

  11. M. Imran, M.K. Siddiqui, M. Naeem, M.A. Iqbal, On topological properties of symmetric chemical structures. Symmetry 10(173), 1–21 (2018)

    Google Scholar 

  12. T. Kambe, R. Sakamoto, K. Hoshiko, K. Takada, M. Miyachi, J.H. Ryu, H. Nishihara, \(\pi \)-Conjugated nickel bis (dithiolene) complex nanosheet. J. Am. Chem. Soc. 135(7), 2462–2465 (2013)

    Article  Google Scholar 

  13. S. Manzoor, M.K. Siddiqui, S. Ahmad, On entropy measures of molecular graphs using topological indices. Arab. J. Chem. 13(8), 6285–6298 (2020)

    Article  Google Scholar 

  14. A. Mehler, Lücking, A., & Weib, P., A network model of interpersonal alignment in dialog. Entropy 12(6), 1440–1483 (2010)

  15. H. Morowitz, Some order-disorder considerations in living systems. Bull. Math. Biophys. 17, 81–86 (1953)

    Article  Google Scholar 

  16. A. Mowshowitz, M. Dehmer, Entropy and the complexity of graphs revisited. Entropy 14, 559–570 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  17. H. Quastler, Information theory in biology. Bull. Math. Biol. 18, 183–185 (1954)

  18. N. Rashevsky, Life, information theory, and topology. Bull. Math. Biol. 17, 229–235 (1955)

    MathSciNet  Google Scholar 

  19. C.E. Shannon, A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 5(1), 3–55 (2001)

    Article  MathSciNet  Google Scholar 

  20. C.E. Shannon, A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948)

    Article  MathSciNet  Google Scholar 

  21. D. Sheberla, L. Sun, M.A. Blood-Forsythe, S. Er, C.R. Wade, C.K. Brozek, M. Dinca, High electrical conductivity in Ni\(_3 (2, 3, 6, 7, 10, 11\)-hexaiminotriphenylene) 2, a semiconducting metal–organic graphene analogue. J. Am. Chem. Soc. 136(25), 8859–8862 (2014)

    Article  Google Scholar 

  22. M.K. Siddiqui, M. Imran, A. Ahmad, On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 280, 132–139 (2016)

    MathSciNet  MATH  Google Scholar 

  23. M.K. Siddiqui, M. Naeem, N.A. Rahman, M. Imran, Computing topological indicesof certain networks. J. Optoelectron. Adv. Mater. 18(9–10), 884–892 (2016)

    Google Scholar 

  24. Z. Shao, J. Amjadi, S.M. Sheikholeslami, M. Valinavaz, On the total double Roman domination. IEEE Access 7, 52035–52041 (2019)

    Article  Google Scholar 

  25. Z. Shao, M. Liang, X. Xu, Some new optimal generalized Sidon sequences. Ars Comb. 107, 369–378 (2012)

    MathSciNet  MATH  Google Scholar 

  26. Z. Shao, P. Wu, X. Zhang, D. Dimitrov, J.B. Liu, On the maximum ABC index of graphs with prescribed size and without pendent vertices. IEEE Access 6, 27604–27616 (2018)

    Article  Google Scholar 

  27. R.V. Sol, S.I. Valverde, Information theory of complex networks: on evolution and architectural constraints. Complex Netw. Lect. Notes Phys. 650, 189–207 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  28. E. Trucco, A note on the information content of graphs. Bull. Math. Biol. 18(2), 129–135 (1956)

    MathSciNet  Google Scholar 

  29. Y.J. Tan, J. Wu, Network structure entropy and its application to scale-free networks. Syst. Eng. Theory Pract. 6, 1–3 (2004)

    Google Scholar 

  30. R.E. Ulanowicz, Quantitative methods for ecological network analysis. Comput. Biol. Chem. 28, 321–339 (2004)

    Article  Google Scholar 

  31. S. Wang, Z. Shao, J.B. Liu, B. Wei, The bounds of vertex Padmakar–Ivan index on k-trees. Mathematics 7(4), 324 (2019)

    Article  Google Scholar 

  32. Q. Zhou, J. Wang, T.S. Chwee, G. Wu, X. Wang, Q. Ye, S.W. Yang, Topological insulators based on 2D shape-persistent organic ligand complexes. Nanoscale 7(2), 727–735 (2015)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, COMSATS University Islamabad, Lahore Campus, Lahore, Pakistan

    Shazia Manzoor, Muhammad Kamran Siddiqui & Sarfraz Ahmad

Authors
  1. Shazia Manzoor
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Muhammad Kamran Siddiqui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sarfraz Ahmad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shazia Manzoor.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Manzoor, S., Siddiqui, M.K. & Ahmad, S. On physical analysis of degree-based entropy measures for metal–organic superlattices. Eur. Phys. J. Plus 136, 287 (2021). https://doi.org/10.1140/epjp/s13360-021-01275-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-021-01275-5

Search

Navigation