Photon blockade in a system consisting of two optomechanical cavities via photon hopping

Abstract

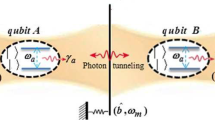
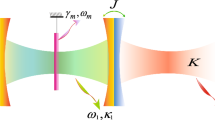
Photon blockade is an updated effect having potential application in many scientific fields such as optical communication and quantum information processing. In this paper, we investigate this phenomenon in a system with two coupled optomechanical cavities. Each cavity possesses a movable mirror connected to each other by a coupling constant of $\xi$ (photon hopping occurs). We consider the effect of optical cavity loss on the Hamiltonian system phenomenologically (using a non-Hermitian Hamiltonian). Due to the low intensity of the considered pump laser, the study is limited to Hilbert space states with two-photon excitations. To achieve the purpose of paper, in the study of the photon statistics, we analyze the equal-time second-order correlation function $g^{(2)}(0)$ for the cavity radiation field. The obtained results show that by tuning the photon hopping rate between the two cavities, photon blockade can be observed at different frequencies. Also, by reducing the cavity decay rate, the minimum of the second-order correlation function decreases, and the photon blockade is more likely to occur.

Appendix. A

In this appendix, we arrive at the probability amplitudes in the steady-state regime that is introduced in Eq. (12). Using the time-dependent Schrödinger equation, $i \frac{\partial }{\partial t}|\psi (t)\rangle ={\hat{H}}_{\text {tot}} |\psi (t)\rangle$, six coupled differential equations are obtained as:

$$\begin{aligned} \dot{C}_{0,0,m_1,m_2}&=- i E_{0,0,m_1,m_2}^\prime C_{0,0,m_1,m_2}-\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle , \nonumber \\ \dot{C}_{0,1,m_1,m_2}&=- (i E_{0,1,m_1,m_2}^\prime +\dfrac{\kappa }{2}) C_{0,1,m_1,m_2}+i\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,0,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(0)\rangle \nonumber \\&\quad -\sqrt{2} \varepsilon \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,2,l_1,l_2}\langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(2)\rangle , \nonumber \\ \dot{C}_{1,0,m_1,m_2}&=- (i E_{1,0,m_1,m_2}^\prime +\dfrac{\kappa }{2}) C_{1,0,m_1,m_2}+i\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(0)\rangle \nonumber \\&\quad -\sqrt{2} \varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{2,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(2),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{1,1,m_1,m_2}&=- (i E_{1,1,m_1,m_2}^\prime +\kappa ) C_{1,1,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,2,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(2)\rangle \nonumber \\&\quad +i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{2,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(2),{\tilde{l}}_2(0)\rangle -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{2,0,m_1,m_2}&=- (i E_{2,0,m_1,m_2}^\prime +\kappa ) C_{2,0,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad - \sqrt{2}\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2}\langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{0,2,m_1,m_2}&=- (i E_{0,2,m_1,m_2}^\prime +\kappa ) C_{0,2,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(2)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad - \sqrt{2}\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle , \end{aligned}$$

(A.1)

where $E^\prime _{n_1,n_2,2,m_1,m_2}=\varDelta _c(n_1+n_2)+\omega _m (m_1+m_2)-\varDelta _g(n_1^2+n_2^2)$ are the energy eigenvalues of the Hamiltonian ${{\hat{H}}}_1^\prime$ in Eq. (8). The following relation can also be established:

$$\begin{aligned} \begin{aligned}&\langle {\tilde{m}}_1(n_1^ \prime ),{\tilde{m}}_2(n_2^\prime )|\left. {{\tilde{1}}_1(n_1),{\tilde{l}}_2(n_2)}\right\rangle = \langle m_1, m_2| \prod _{i= 1} ^{2}\exp \left[ {\frac{g_0}{\omega _m}( n_i-n_i^\prime ) ({\hat{b}}^{\dagger }_{i}-{\hat{b}}_{i})}\right] |l_1,l_2\rangle . \end{aligned} \end{aligned}$$

(A.2)

As previously mentioned, only a few photons are possible to be excited in the weak pump regime. In the limit $\varepsilon _p\rightarrow 0$, the two modes of the cavities remain in the ground state. Therefore, $C_{0,1,m_1,m_2}$ and $C_{1,0,m_1,m_2}$ are on the scale $\varepsilon _p$, $C_{1,1,m_1,m_2}$, $C_{0,2,m_1,m_2}$ and $C_{2,0,m_1,m_2}$ which are on the scale $\varepsilon _p^2$ and its higher order can be discarded in the weak pump regime. This method has been widely used in optomechanical systems to study the photon statistics [23, 29, 31]. Accordingly, the equations in (A.1) can be simplified as follows:

$$\begin{aligned} \dot{C}_{0,0,m_1,m_2}&=- i E^\prime _{0,0,m_1,m_2} C_{0,0,m_1,m_2}, \nonumber \\ \dot{C}_{0,1,m_1,m_2}&=- (i E^\prime _{0,1,m_1,m_2}+\dfrac{\kappa }{2}) C_{0,1,m_1,m_2}+i\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,0,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{1,0,m_1,m_2}&=- (i E^\prime _{1,0,m_1,m_2}+\dfrac{\kappa }{2}) C_{1,0,m_1,m_2}+i\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{1,1,m_1,m_2}&=- (i E^\prime _{1,1,m_1,m_2}+\kappa ) C_{1,1,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,2,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(2)\rangle \\&\quad +i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{2,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(2),{\tilde{l}}_2(0)\rangle -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad -\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(1),{\tilde{m}}_2(1)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{2,0,m_1,m_2}&=- (i E^\prime _{2,0,m_1,m_2}+\kappa ) C_{2,0,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad - \sqrt{2}\varepsilon \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,0,l_1,l_2} \langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(1),{\tilde{l}}_2(0)\rangle , \nonumber \\ \dot{C}_{0,2,m_1,m_2}&=- (i E^\prime _{0,2,m_1,m_2}+\kappa ) C_{0,2,m_1,m_2}+i \sqrt{2}\xi \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{1,1,l_1,l_2} \langle {\tilde{m}}_1(0),{\tilde{m}}_2(2)|{\tilde{l}}_1(1),{\tilde{l}}_2(1)\rangle \nonumber \\&\quad - \sqrt{2}\varepsilon _p \displaystyle \sum _{l_1,l_2=0}^{\infty } C_{0,1,l_1,l_2} \langle {\tilde{m}}_1(2),{\tilde{m}}_2(0)|{\tilde{l}}_1(0),{\tilde{l}}_2(1)\rangle \nonumber . \end{aligned}$$

(A.3)

To get the probability amplitudes, it is assumed that the mechanical modes are initially in the vacuum state and always being stable in the photon-dependent displaced number states $|{\tilde{0}}(n_1),{\tilde{0}}(n_2)\rangle$ $(n_1, n_2=0,1,2)$ during the dynamical evolution. Using this assumption and notifying Eq. (A.2), the probability amplitudes in the steady-state regime are achieved as follows:

$$\begin{aligned} \begin{aligned} C_{0,0,0,0}&=1, \\ C_{0,1,0,0}= C_{1,0,0,0}&=-\dfrac{2 \varepsilon _p e^{\dfrac{1}{2} \left( \dfrac{g_0}{\omega _m}\right) ^2}}{e^{\left( \dfrac{g_0}{\omega _m}\right) ^2}[2i(\varDelta _c-\varDelta _g)+\kappa ]-2 i \xi },\\ C_{1,1,0,0}&=-\dfrac{4 \varepsilon _p^2 e^{ \left( \dfrac{g_0}{\omega _m}\right) ^2}\left( e^{ \left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2i(\varDelta _c-2\varDelta _g)+\kappa \right) +2 i \xi \right) }{\left( e^{\left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2(\varDelta _c-\varDelta _g)-i\kappa \right) -2 \xi \right) \left( e^{2\left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2(\varDelta _c-2\varDelta _g)-i\kappa \right) \left( 2 i (\varDelta _c-\varDelta _g)+\kappa \right) -4 i \xi ^2\right) },\\ C_{2,0,0,0}= C_{0,2,0,0}&=\dfrac{2\sqrt{2} \varepsilon _p^2 e^{ \left( \dfrac{g_0}{\omega _m}\right) ^2}\left( e^{ \left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2(\varDelta _c-\varDelta _g)-i\kappa \right) +2\xi \right) }{\left( e^{\left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2(\varDelta _c-\varDelta _g)-i\kappa \right) -2 \xi \right) \left( e^{2\left( \dfrac{g_0}{\omega _m}\right) ^2}\left( 2i(\varDelta _c-2\varDelta _g)+\kappa \right) \left( 2 i (\varDelta _c-\varDelta _g)+\kappa \right) +4 \xi ^2\right) }. \end{aligned}\nonumber \\ \end{aligned}$$

(A.4)