Non-Gaussian laser pulse response on photo-thermoelastic interactions in a silicon plate under the light of memory-dependent thermoelasticity theory

Abstract

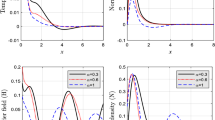
In the present article, the wave propagation in a homogeneous semi-infinite silicon plate through photo-thermal process has been comparatively studied under the light of memory-dependent thermoelasticity theories with thermal relaxations. Without neglecting the coupling between the plasma and thermoelastic waves that photo-generated through intensity modulated beam of non-Gaussian laser pulse, a two-dimensional semiconducting medium having homogeneity in thermal and elastic properties is considered. The analytical solutions were observed in the domain of Laplace–Fourier transform by the method of eigenvalues approach. Finally, suitable graphical discussions and conclusions are presented with respect to varied thermal relaxation times.

Appendix

1.1 Memory-dependent derivatives

Wang and Li [3] defined memory-dependent derivatives (MDDs) in an integral form with a kernel function on a slipping interval as follows:

$$\begin{aligned} D_\omega ^{(1)}f(x,t)=\frac{1}{\omega }\int _{t-\omega }^t k(t-\xi )\frac{\partial f\left( x,\xi \right) }{\partial \xi }\partial \xi \end{aligned}$$

(78)

where $\omega$ is the time delay and $K(t-\omega )$ is the kernel function.

The kernel function should be chosen in such a way such that the magnitude of MDD should be smaller than that of the common partial derivative, and for that the bounds of the kernel should be $0\le k(t-\xi )\le 1$ for $\xi \in [t-\omega ,t]$. This is done to educe the memory effect better than others. The time delay $\omega (>0)$ should always be chosen in such a manner, that the material’s thermodynamical behaviour can be understood more properly.

It is to note that in case $k(t-\xi )=1$ we shall obtain

$$\begin{aligned} D_\omega ^{(1)}f(x,t)=\frac{1}{\omega }\int _{t-\omega }^t \frac{\partial f\left( x,\xi \right) }{\partial \xi } \partial \xi =\dfrac{f(x,t)-f(x,t-\omega )}{\omega } \end{aligned}$$

This implies that as $\omega \rightarrow 0$, MDD tends to common partial derivative of first order. The kernel shows a monotone nature with $K=0$ for the past time $t-\xi$ and $K=1$ for the present time t.

During the year 2017, Ezzat and his co-workers [6] have proposed a form of the memory kernel, which is as follows:

$$\begin{aligned} k(t-p)=1-\frac{2b}{\omega }\left( t-p\right) +\frac{a^2\left( t-p\right) ^2}{\omega ^2} \end{aligned}$$

(79)

a and b are the parameters, the values of which are to be chosen.

The Laplace transform of a function containing the MDD with a kernel of the form (79) is:

$$\begin{aligned} \textit{L}\left[ D_\omega f(t)\right]= & {} \frac{{\overline{f}}(s)}{\omega }\left( \left( 1-\frac{2b}{\omega s}+\frac{2a^2}{\omega ^2 s^2}\right) \right. \nonumber \\&\left. - \text {exp}\left( -\omega s\right) \left( 1-2b^2+a^2+\frac{2\left( a^2-b\right) }{\omega s}+\frac{2a^2}{\omega ^2 s^2}\right) \right) \end{aligned}$$

(80)

If the kernel function $k(t,p)=1$, then

$$\begin{aligned} \textit{L}\left[ D_\omega f(t)\right] =\frac{1}{\omega }\left( 1-\text {exp}\left( -\omega s\right) \right) {\overline{f}}(s) \end{aligned}$$

(81)

where ${\overline{f}}(s)$ denotes the Laplace transform of f(t) and $f(t-\omega )=0$ for $t<\omega$.

1.2 Non-Gaussian laser pulse function

The temporal profile of a non-Gaussian laser pulse is defined as

$$\begin{aligned} L_P(t)=\frac{L_0}{t_p^2}te^{-\frac{t}{t_p}} \end{aligned}$$

(82)

where $L_0$ is the laser intensity that is defined as the total energy carried by a laser pulse per unit area of the laser beam, and $t_p$ is the characteristic time of the laser pulse which may also be referred as the time duration of the laser pulse.

The function has the property

$$\begin{aligned} \int _0^\infty L_P(t)\mathrm{d}t=1 \end{aligned}$$

(83)

and

$$\begin{aligned} \max \limits _{\forall t}\left[ L_P(t)\right] =L_P(t_p) \end{aligned}$$

(84)

The following figure provides the temporal profile of the laser power $L_P/L_0$, by considering $tp = 2p$ s (Fig. 12).

Fig. 12

The temporal profile of the laser power $L_P/L_0$

The Laplace transform of Eq. (82) can be easily obtained by using the first shifting property of the transform.

The Laplace transform followed by the Fourier transform of the non-Gaussian laser pulse function is obtained as:

$$\begin{aligned} {\overline{L}}^*(t)=\frac{L_0\delta (p)}{(1+st_p)^2} \end{aligned}$$

(85)