Skip to main content

Advertisement

SpringerLink
Log in

A nonstandard finite difference scheme and optimal control for an HIV model with Beddington–DeAngelis incidence and cure rate

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

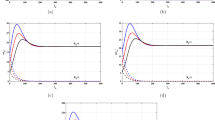
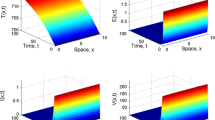
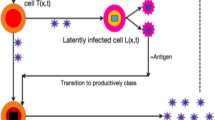
In this paper, we incorporate the Beddington–DeAngelis incidence rate to a continuous-time HIV infection model with cure rate and a full logistic proliferation rate of \(CD4^+\) T cells in both uninfected and infected cells. Equilibria and their local stability analysis are discussed. It is shown that the HIV-free equilibrium point is locally asymptotically stable if \({\mathcal {R}}_0<1\) and unstable if \({\mathcal {R}}_0\ge 1\), where \({\mathcal {R}}_0\) is the basic reproduction number. Whereas, the HIV equilibrium point is locally asymptotically stable if \({\mathcal {R}}_0>1\). A nonstandard finite difference method is applied to the continuous model to obtain its discrete counterpart. The scheme applied preserves the main features of the continuous model such as positivity, boundedness of the solutions, equilibria and their local stability. Moreover, an optimal control strategy is applied to the discrete-time model in order to reduce the number of infected cells as well as the number of free HIV particles. Numerical simulations are performed to verify the theoretical analysis obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. D.M. Imboden, S. Pfenninger, Introduction to Systems Analysis: Mathematically Modeling Natural Systems (Springer, Berlin, 2013)

    MATH  Google Scholar 

  2. B.P. Ingalls, Mathematical Modeling in Systems Biology: An Introduction (MIT Press, London, 2013)

    MATH  Google Scholar 

  3. A. Eladdadi, P. Kim, D. Mallet, Mathematical Models of Tumor-Immune System Dynamics (Springer, New York, 2014)

    MATH  Google Scholar 

  4. S.M. Salman, E. Ahmed, A mathematical model for Creutzfeldt Jacob Disease (CJD). Chaos Solitons Fract. 116, 249–260 (2018)

    MathSciNet  MATH  ADS  Google Scholar 

  5. A.S. Perelson, A.U. Neumann, M. Markowitz, J.M. Leonard, D.D. Ho, HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science 271, 1582–1586 (1996)

    ADS  Google Scholar 

  6. M.A. Nowak, S. Bonhoeffer, G.M. Shaw, R.M. May, Anti-viral drug treatment: dynamics of resistance in free virus and infected cell populations. J. Theor. Biol. 184, 203–217 (1997)

    Google Scholar 

  7. S. Bonhoeffer, R.M. May, G.M. Shaw, M.A. Nowak, Virus dynamics and drug therapy. Proc. Natl. Acad. Sci. USA 94, 6971–6976 (1997)

    ADS  Google Scholar 

  8. M.A. Stafford, L. Corey, Y.Z. Cao, E.S. Daar, D.D. Ho, A.S. Perelson, Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol. 203, 285–293 (2000)

    Google Scholar 

  9. L. Guihua, J. Zhen, Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Solitons Fract. 25(5), 1177–1184 (2005)

    MathSciNet  MATH  Google Scholar 

  10. A. Tripathi, R. Naresh, D. Sharma, Modelling the effect of screening of unaware infectives on the spread of HIV infection. Appl. Math. Comput. 184, 1053–1068 (2007)

    MathSciNet  MATH  Google Scholar 

  11. Z. Mukandavire, A.B. Gumel, W. Garira, J.M. Tchuenche, Mathematical analysis of a model for HIV-Malaria co-infection. Math. Biosci. Eng. 6, 333–362 (2009)

    MathSciNet  MATH  Google Scholar 

  12. E.A. Hernandez-Vargasa, R.H. Middleton, Modeling the three stages in HIV infection. J. Theor. Biol. 320, 33–40 (2013)

    MathSciNet  MATH  Google Scholar 

  13. A. Mastroberardino, Y. Cheng, A. Abdelrazec, H. Liu, Mathematical modeling of the HIV/AIDS epidemic in Cuba. Int. J. Biomath. 08, 1550047 (2015). https://doi.org/10.1142/S1793524515500473

    Article  MathSciNet  MATH  Google Scholar 

  14. L. Cai, X. Li, M. Ghosh, B. Guo, Stability analysis of HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 229, 313–323 (2009)

    MathSciNet  MATH  ADS  Google Scholar 

  15. A.D. AlAgha, A.M. Elaiw, Stability of a general reaction-diffusion HIV-1 dynamics modelwith humoral immunity. Eur. Phys. J. Plus 134, 390 (2019). https://doi.org/10.1140/epjp/i2019-12740-9

    Article  Google Scholar 

  16. G. Nazir, K. Shah, A. Debbouche, R.A. Khan, Study of HIV mathematical model under nonsingular kernel type derivative of fractional order. Chaos Solitons Fract. 139, 110095 (2020)

    MathSciNet  ADS  Google Scholar 

  17. F. Haq, K. Shah, G.U.R.- Rahman, M. Shahzad, Numerical analysis of fractional order model of HIV-1 infection of CD4\(^+\) T-cells. Comput. Methods Differ. Equ. 5(1), 1–11 (2017)

  18. S. Bushnaq, S.A. Khan, K. Shah, G. Zaman, Existence theory of HIV-1 infection model by using arbitrary order derivative of without singular kernel type. J. Math. Anal. 9(1), 16–28 (2018)

    MathSciNet  Google Scholar 

  19. S. Bushnaq, S.A. Khan, K. Shah, G. Zaman, Mathematical analysis of HIV/AIDS infection model with Caputo-Fabrizio fractional derivative. Cogent Math. Stat. 5(1), 1432521 (2018)

    MathSciNet  MATH  Google Scholar 

  20. S.M. Salman, Memory and media coverage effect on an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 385 (2021)

  21. R. Luckheeram, R. Zhou, A. Verma et al., CD4\(+\) T cells: differentiation and functions. Clin. Dev. Immunol. 28, 445–489 (2012). https://doi.org/10.1155/2012/925135

    Article  Google Scholar 

  22. J. Zhu, W.E. Paul, CD4 T cells: fates, functions, and faults. Blood 112(5), 15571569 (2008)

    Google Scholar 

  23. L.C. Wang, M.Y. Li, Mathematical analysis of the global dynamics of a model for HIV infection of \(CD4^+\) T cells. Math. Biosci. 200, 44–57 (2006)

    MathSciNet  MATH  Google Scholar 

  24. X. Wang, X.Y. Song, Global stability and periodic solution of a model for HIV infection of \(CD4^+\) T cells. Appl. Math. Comput. 189, 1331–1340 (2007)

    MathSciNet  MATH  Google Scholar 

  25. L. Cai, X. Li, Stability of Hopf bifurcation in a delayed model for HIV infection of CD4+ T-cells. Chaos Solitons Fract. 42, 1–11 (2009)

    MATH  ADS  Google Scholar 

  26. P.K. Srivastava, P. Chandra, Modeling the dynamics of HIV and \(CD4^+\) T cells during primary infection. Nonlinear Anal. Real World Appl. 11, 612–618 (2010)

    MathSciNet  MATH  Google Scholar 

  27. S. Wang, P. Hottz, M. Schechter, L. Rong, Modeling the slow \(CD4^+\) T cell decline in HIV-infected individuals. PLoS. Comput. Biol. 11(12), e1004665 (2015)

    Google Scholar 

  28. H. Takata, C. Kessing, A. Sy, N. Lima, J. Sciumbata, L. Mori, R.B. Jones et al., Modeling HIV-1 latency using primary \(CD4^+\) T cells from virally suppressed HIV-1-infected individuals on antiretroviral therapy. J. Virol. 93, e02248–18 (2018). https://doi.org/10.1128/JVI.02248-18

    Article  Google Scholar 

  29. A.S. Perelson, P.W. Nelson, Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 41, 3–44 (1999)

    MathSciNet  MATH  ADS  Google Scholar 

  30. X.Y. Song, A.U. Neumann, Global stability and periodic solution of the viral dynamics. J. Math. Anal. Appl. 329, 281–297 (2007)

    MathSciNet  MATH  Google Scholar 

  31. X. Liu, H. Wang, Z. Hu, W. Ma, Global stability of an HIV pathogenesis model with cure rate. Nonlinear Anal. Real World Appl. 12(6), 2947–2961 (2011)

    MathSciNet  MATH  Google Scholar 

  32. X.Y. Zhou, X.Y. Song, X.Y. Shi, A differential equation model of HIV infection of \(CD4^+\) T-cells with cure rate. J. Math. Anal. Appl. 342, 1342–1355 (2008)

    MathSciNet  MATH  Google Scholar 

  33. L.G. Guidotti, R. Rochford, J. Chung, M. Shapiro, R. Purcell, F.V. Chisari, Viral clearance without destruction of infected cells during acute HBV infection. Science 284, 825–829 (1999)

    ADS  Google Scholar 

  34. S. Lewin, T. Walters, S. Locarnini, Hepatitis B treatment: rational combination chemotherapy based on viral kinetic and animal model studies. Antivir. Res. 35, 381–396 (2002)

    Google Scholar 

  35. K.F. Wang, A.J. Fan, A. Torres, Global properties of an improved hepatitis B virus model. Nonlinear Anal. Real World Appl. 11, 3131–3138 (2010)

    MathSciNet  MATH  Google Scholar 

  36. J.R. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency. J. Anim. Ecol. 44, 331–340 (1975)

    Google Scholar 

  37. D.L. DeAngelis, R.A. Goldstein, R.V. ONeill, A model for trophic interaction. Ecology 56, 881–892 (1975)

  38. A. Elaiw, I. Hassanien, S. Azoz, Global stability of HIV infection models with intracellular delays. J. Korean Math. Soc. 49, 779–794 (2012)

    MathSciNet  MATH  Google Scholar 

  39. G. Huang, W. Ma, Y. Takeuchi, Global analysis for delay virus dynamics model with Beddington-DeAngelis functional response. Appl. Math. Lett. 24, 1199–1203 (2011)

    MathSciNet  MATH  Google Scholar 

  40. X. Wang, Y. Tao, X. Song, A delayed HIV-1 infection model with Beddington-DeAngelis functional response. Nonlinear Dyn. 62, 67–72 (2010)

    MathSciNet  MATH  Google Scholar 

  41. C. Lv, L. Huang, Z. Yuan, Global stability for an HIV-1 infection model with Beddington-DeAngelis incidence rate and CTL immune response. Commun. Nonlinear Sci. Numer. Simul. 19, 121–7 (2014)

    MathSciNet  MATH  ADS  Google Scholar 

  42. Y. Liu, J. Xiong, C. Hu, C. Wu, Stability analysis for fractional differential equations of an HIV infection model with cure rate, in IEEE International Conference on Information and Automation (ICIA), Ningbo, pp. 707–711 (2016). https://doi.org/10.1109/ICInfA.2016.7831911

  43. C.S. Holling, The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91(5), 293–320 (1959). https://doi.org/10.4039/Ent91293-5

    Article  Google Scholar 

  44. X. Song, A. Neumann, Global stability and periodic solution of the viral dynamics. J. Math. Anal. Appl. 329, 281–297 (2007)

    MathSciNet  MATH  Google Scholar 

  45. Z. Hu, Z. Teng, H. Jiang, Stability analysis in a class of discrete SIRS epidemic models. Nonlinear Anal. Real World Appl. 13, 2017–2033 (2012)

    MathSciNet  MATH  Google Scholar 

  46. A. Suryanto, A dynamically consistent nonstandard numerical scheme for epidemic model with saturated incidence rate. Int. J. Math. Comput. 13, 112–123 (2011)

    MathSciNet  Google Scholar 

  47. A. Suryanto, Stability and bifurcation of a discrete SIS epidemic model with delay, in Proceedings of the 2nd International Conference on Basic Sciences, Indonesia, pp. 1–6 (2012)

  48. Q. Cui, J. Xu, Q. Zhang, K. Wang, An NSFD scheme for SIR epidemic models of childhood diseases with constant vaccination strategy. Adv. Differ. Equ. 2014, 172 (2014)

    MathSciNet  MATH  Google Scholar 

  49. K.E. Atkinson, W. Han, D.E. Stewart, Numerical Solution of Ordinary Differential Equations (Wiley, Portsmouth, 2009)

    MATH  Google Scholar 

  50. R.E. Mickens, Nonstandard Finite Difference Models of Differential equations (World Scientific Publishing Co., River Edge, 1994)

    MATH  Google Scholar 

  51. Y. Geng, J.H. Xu, J.Y. Hou, Discretization and dynamic consistency of a delayed and diffusive viral infection model. Appl. Math. Comput. 316, 282–295 (2018)

    MathSciNet  MATH  Google Scholar 

  52. K. Hattaf, N. Yousfi, A numerical method for a delayed viral infection model with general incidence rate. J. King Saud Univ. Sci. 28, 368–374 (2016)

    MATH  Google Scholar 

  53. K. Hattaf, N. Yousfi, Global properties of a discrete viral infection model with general incidence rate. Math. Methods Appl. Sci. 39, 998–1004 (2016)

    MathSciNet  MATH  ADS  Google Scholar 

  54. A. Korpusik, A nonstandard finite difference scheme for a basic model of cellular immune response to viral infection. Commun. Nonlinear Sci. Numer. Simul. 43, 369–384 (2017)

    MathSciNet  MATH  ADS  Google Scholar 

  55. K. Manna, S.P. Chakrabarty, Global stability and a non-standard finite difference scheme for a diffusion driven HBV model with capsids. J. Differ. Equ. Appl. 21, 918–933 (2015)

    MathSciNet  MATH  Google Scholar 

  56. P.L. Shi, L.Z. Dong, Dynamical behaviors of a discrete HIV-1 virus model with bilinear infective rate. Math. Methods Appl. Sci. 37, 2271–2280 (2013)

    MathSciNet  MATH  Google Scholar 

  57. Y. Yang, J.L. Zhou, X.S. Ma, T.H. Zhang, Nonstandard finite difference scheme for a diffusive within-host virus dynamics model both virus-to-cell and cell-to-cell transmissions. Comput. Math. Appl. 72, 1013–1020 (2016)

    MathSciNet  MATH  Google Scholar 

  58. J.L. Zhou, Y. Yang, Global dynamics of a discrete viral infection model with time delay, virus-to-cell and cell-to-cell transmissions. J. Differ. Equ. Appl. 23, 1853–1868 (2017)

    MathSciNet  MATH  Google Scholar 

  59. X. Zhuang, Q. Wang, J. Wen, Numerical dynamics of nonstandard finite difference method for nonlinear delay differential equation. Int. J. Bifurc. Chaos. 28(11), 1850133 (2018)

    MathSciNet  MATH  Google Scholar 

  60. P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)

    MathSciNet  MATH  Google Scholar 

  61. J.S. Muldowney, Compound matrices and ordinary differential equations. Rocky Mt. J. Math. 20, 857–872 (1990)

    MathSciNet  MATH  Google Scholar 

  62. J. Arino, C.C. McCluskey, P. van den Driessche, Global results for an epidemic model with vaccination that exhibits backward bifurcation. SIAM J. Appl. Math. 64, 260–276 (2003)

    MathSciNet  MATH  Google Scholar 

  63. C.C. McCluskey, P. van den Driessche, Global analysis of two tuberculosis models. J. Dyn. Differ. Equ. 16, 139–166 (2004)

    MathSciNet  MATH  Google Scholar 

  64. R.E. Mickens, Dynamics consistency: a fundamental principle for constructing nonstandard finite difference scheme for differential equation. J. Differ. Equ. Appl. 11, 645–653 (2005)

    MathSciNet  MATH  Google Scholar 

  65. R.E. Mickens, Numerical integration of population models satisfying conservation laws: NSFD methods. J. Biol. Dyn. 1, 427–436 (2007)

    MathSciNet  MATH  Google Scholar 

  66. S.N. Elaydi, An Introduction to Difference Equations. Undergraduate Texts in Mathematics, 2nd edn. (Springer, New York, 1999)

  67. S. Jang, S. Elaydi, Difference equations from discretization of a continuous epidemic model with immigration of infectives. Can. Appl. Math. Q. 11, 93–105 (2004)

    MathSciNet  MATH  Google Scholar 

  68. L. Edelstein-Keshet, Mathematical Models in Biology (McGraw-Hill, New York, 1988)

    MATH  Google Scholar 

  69. M.A. Khan, S.W. Shah, S. Ullah, J.F. Gomez-Aguilar, A dynamical model of asymptomatic carrier Zika virus with optimal control strategies. Nonlinear Anal. Real World Appl. 50, 144–170 (2019)

    MathSciNet  MATH  Google Scholar 

  70. S. Ullah, M.A. Khan, J.F. Gomez-Aguilar, Mathematical formulation of hepatitis B virus with optimal control analysis. Optim. Control Appl. Methods 40(3), 529–544 (2019)

    MathSciNet  MATH  Google Scholar 

  71. E. Bonyah, M.A. Khan, K.O. Okosun, J.F. Gomez-Aguilar, On the co-infection of dengue fever and Zika virus. Optim. Control Appl. Methods 40(3), 394–421 (2019)

    MathSciNet  MATH  Google Scholar 

  72. E. Bonyah, M.A. Khan, K.O. Okosun, J.F. Gomez-Aguilar, Modelling the effects of heavy alcohol consumption on the transmission dynamics of gonorrhea with optimal control. Math. Biosci. 309, 1–11 (2019)

    MathSciNet  MATH  Google Scholar 

  73. E. Bonyah, J.F. Gomez-Aguilar, A. Adu, Stability analysis and optimal control of a fractional human African trypanosomiasis model. Chaos Solitons Fract. 117, 150–160 (2018)

    MathSciNet  MATH  ADS  Google Scholar 

  74. W.H. Fleming, R.W. Rishel, Deterministic and Stochastic Optimal Control (Springer, New York, 1975)

    MATH  Google Scholar 

  75. D.L. Lukes, Differential Equations: Classical to Controlled, Mathematics in Science and Engineering, vol. 162 (Academic Press, New York, 1982)

    Google Scholar 

  76. L.S. Pontryagin, V.G. Boltyanskii, R.V. Gamkrelidze, E.F. Mishchenko, The Mathematical Theory of Optimal Processes (Wiley, New York, 1962)

    MATH  Google Scholar 

Download references

Acknowledgements

The author would like to thank the anonymous reviewers for providing valuable comments which helped to improve the original manuscript.

Author information

Authors and Affiliations

  1. Mathematics Department, Faculty of Education, Alexandria University, Alexandria, Egypt

    Sanaa Moussa Salman

Authors
  1. Sanaa Moussa Salman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sanaa Moussa Salman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Salman, S.M. A nonstandard finite difference scheme and optimal control for an HIV model with Beddington–DeAngelis incidence and cure rate. Eur. Phys. J. Plus 135, 808 (2020). https://doi.org/10.1140/epjp/s13360-020-00839-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00839-1

Search

Navigation