Investigation of surface effects on the natural frequency of a functionally graded cylindrical nanoshell based on nonlocal strain gradient theory

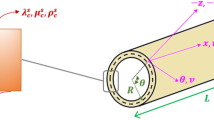
Abstract

In submicron structures, because of surface and small-scale effects, the classical continuum theory does not lead to accurate results. In order to use this method in the study of the mechanical behavior of such structures, surface elasticity and size-dependent theories have been introduced. In this paper, by simultaneously applying the theories of Gurtin–Murdoch surface elasticity and the nonlocal strain gradient, the vibration behavior of a functionally graded nanoshell has been investigated. To this end, the governing motion equations and related boundary conditions are extracted utilizing Hamilton’s principle and the first-order shear deformation theory of shell and then will be solved by the generalized differential quadrature method. The effects of surface properties such as surface elastic properties, residual surface stress, and surface mass density have been studied. Also, a comparative study between different continuum mechanics theories, with and without surface effects, at different boundary conditions and values of length-to-radius ratio and FG gradient index is presented.

Appendix

The coefficients in Eq. (13) are defined as follows:

$$ \begin{aligned} A_{11}^{*} & = \int\limits_{ - h/2}^{h/2} {\left( {\lambda + 2\mu } \right){\text{d}}z} + \left( {\lambda^{s + } + 2\mu^{s + } } \right){ + }\left( {\lambda^{s - } + 2\mu^{s - } } \right) \\ B_{11}^{*} & = \int\limits_{ - h/2}^{h/2} {\left( {\lambda + 2\mu } \right)zdz} + \frac{h}{2}\left[ {\left( {\lambda^{s + } + 2\mu^{s + } } \right) - \left( {\lambda^{s - } + 2\mu^{s - } } \right)} \right] \\ D_{11}^{*} & = \int\limits_{ - h/2}^{h/2} {\left( {\lambda + 2\mu } \right)z^{2} dz} + \frac{{h^{2} }}{4}\left[ {\left( {\lambda^{s + } + 2\mu^{s + } } \right) + \left( {\lambda^{s - } + 2\mu^{s - } } \right)} \right] \\ A_{12}^{*} & = \int\limits_{ - h/2}^{h/2} {\lambda {\text{d}}z} + \left( {\lambda^{s + } + \tau^{s + } } \right) + \left( {\lambda^{s - } + \tau^{s - } } \right) \\ B_{12}^{*} & = \int\limits_{ - h/2}^{h/2} {\lambda z{\text{d}}z} + \frac{h}{2}\left[ {\left( {\lambda^{s + } + \tau^{s + } } \right) - \left( {\lambda^{s - } + \tau^{s - } } \right)} \right] \\ D_{12}^{*} & = \int\limits_{ - h/2}^{h/2} {\lambda z^{2} {\text{d}}z} + \frac{{h^{2} }}{4}\left[ {\left( {\lambda^{s + } + \tau^{s + } } \right) + \left( {\lambda^{s - } + \tau^{s - } } \right)} \right] \\ A_{66}^{*} & = \int\limits_{ - h/2}^{h/2} {\mu {\text{d}}z} + \left( {\mu^{s + } + \mu^{s - } } \right) - \frac{1}{2}\left( {\tau^{s + } + \tau^{s - } } \right) ,\quad A_{66} = \int\limits_{ - h/2}^{h/2} {\mu {\text{d}}z} \\ B_{66}^{*} & = \int\limits_{ - h/2}^{h/2} {\mu z{\text{d}}z} + \frac{h}{2}\left( {\mu^{s + } - \mu^{s - } } \right) - \frac{h}{4}\left( {\tau^{s + } - \tau^{s - } } \right) \\ D_{66}^{*} & = \int\limits_{ - h/2}^{h/2} {\mu z^{2} {\text{d}}z} + \frac{{h^{2} }}{4}\left( {\mu^{s + } + \mu^{s - } } \right) - \frac{{h^{2} }}{8}\left( {\tau^{s + } + \tau^{s - } } \right) \\ a_{1} & = \left( {\tau^{s + } + \tau^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }f\left( z \right){\text{d}}z} + \left( {\tau^{s + } - \tau^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }\frac{1}{2}{\text{d}}z} \\ b_{1} & = \left( {\tau^{s + } + \tau^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }zf\left( z \right){\text{d}}z} + \left( {\tau^{s + } - \tau^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }\frac{z}{2}{\text{d}}z} \\ a_{2} & = \left( {\rho^{s + } + \rho^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }f\left( z \right){\text{d}}z} + \left( {\rho^{s + } - \rho^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }\frac{1}{2}{\text{d}}z} \\ b_{2} & = \left( {\rho^{s + } + \rho^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }zf\left( z \right){\text{d}}z} + \left( {\rho^{s + } - \rho^{s - } } \right)\int\limits_{ - h/2}^{h/2} {\frac{\lambda }{2\mu }\frac{z}{2}{\text{d}}z} \\ \end{aligned} $$