Skip to main content
SpringerLink
Log in

Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

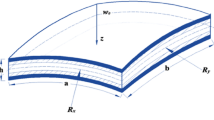
This paper is concerned with the free vibration and transient response of graphene platelets reinforced functionally graded (GPL-FG) cylindrical shell resting on elastic foundation by utilizing the Chebyshev–Lagrangian approach. The boundary constraints are realized by setting reasonable values of stiffness of the artificial virtual springs. According to FSDT, the analysis model of GPL-FG cylindrical shell is established. Then, the displacement fields are expanded in terms of the Chebyshev–Lagrangian approach. Based on the work above, Rayleigh–Ritz energy method is employed to solve the unknown coefficients of Chebyshev expansions with purpose to indicate the dynamic characteristics of the analysis model. In addition, the Rayleigh damping coefficients are taken into account to investigate the transient response results from the external excitation. A series of numerical results show the rapid convergence and precision of the present method by comparison with results obtained by the published papers and FEM. Ultimately, the analysis about the effects of parameters and factors on free vibration and transient response are discussed, including geometry and material properties, boundary conditions, stiffness of elastic foundation, loading types and Rayleigh damping coefficients.

Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  1. D.N. Paliwal, R.K. Pandey, T. Nath, Free vibrations of circular cylindrical shell on Winkler and Pasternak foundations. Int. J. Press. Vessels Pip. 69(1), 79–89 (1996)

    Google Scholar 

  2. E. Bagherizadeh, Y. Kiani, M.R. Eslami, Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Compos. Struct. 93(11), 3063–3071 (2011)

    Google Scholar 

  3. M. Koizumi, FGM activities in Japan. Compos. B Eng. 28(1), 1–4 (1997)

    MathSciNet  Google Scholar 

  4. G. Catania, M. Strozzi, Damping oriented design of thin-walled mechanical components by means of multi-layer coating technology. Coatings 8, 73 (2018)

    Google Scholar 

  5. E. Demir, Vibration and damping behaviors of symmetric layered functional graded sandwich beams. Struct. Eng. Mech. 62(6), 771–780 (2017)

    Google Scholar 

  6. L. Yu, Y. Ma, C. Zhou et al., Damping efficiency of the coating structure. Int. J. Solids Struct. 42(11), 3045–3058 (2005)

    MATH  Google Scholar 

  7. T.Y. Ng, K.Y. Lam, K.M. Liew et al., Dynamic stability analysis of functionally graded cylindrical shells under periodic axial loading. Int. J. Solids Struct. 38(8), 1295–1309 (2001)

    MATH  Google Scholar 

  8. S.C. Pradhan, C.T. Loy, K.Y. Lam et al., Vibration characteristics of functionally graded cylindrical shells under various boundary conditions. Appl. Acoust. 61(1), 111–129 (2000)

    Google Scholar 

  9. C.T. Loy, K.Y. Lam, J.N. Reddy, Vibration of functionally graded cylindrical shells. Int. J. Mech. Sci. 41(3), 309–324 (1999)

    MATH  Google Scholar 

  10. M.M. Najafizadeh, M.R. Isvandzibaei, Vibration of functionally graded cylindrical shells based on different shear deformation shell theories with ring support under various boundary conditions. J. Mech. Sci. Technol. 23(8), 2072–2084 (2009)

    Google Scholar 

  11. A.G. Shah, T. Mahmood, M.N. Naeem, Vibrations of FGM thin cylindrical shells with exponential volume fraction law. Appl. Math. Mech. 030(005), 607–615 (2009)

    MATH  Google Scholar 

  12. Z. Iqbal, M.N. Naeem, N. Sultana, Vibration characteristics of FGM circular cylindrical shells using wave propagation approach. Acta Mech. 208(3–4), 237–248 (2009)

    MATH  Google Scholar 

  13. K. Mercan, Ç. Demir, Ö. Civalek, Vibration analysis of FG cylindrical shells with power-law index using discrete singular convolution technique. Curved Layer Struct. 3, 82–90 (2016)

    Google Scholar 

  14. F. Zhaohua, R.D. Cook, Beam elements on two-parameter elastic foundations. J. Eng. Mech. 109(6), 1390–1402 (1983)

    Google Scholar 

  15. D. Hui, Postbuckling behavior of infinite beams on elastic foundations using Koiter’s improved theory. Int. J. Non-Linear Mech. 23(2), 113–123 (1988)

    ADS  MATH  Google Scholar 

  16. A.H. Sofiyev, D. Hui, A.M. Najafov et al., Influences of shear stresses and rotary inertia on the vibration of functionally graded coated sandwich cylindrical shells resting on the Pasternak elastic foundation. J. Sandwich Struct. Mater. 17(6), 691–720 (2015)

    Google Scholar 

  17. A.H. Sofiyev, Large amplitude vibration of FGM orthotropic cylindrical shells interacting with the nonlinear Winkler elastic foundation. Compos. B Eng. 98, 141–150 (2016)

    Google Scholar 

  18. A.H. Sofiyev, N. Kuruoglu, Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Compos. B Eng. 45(1), 1133–1142 (2013)

    Google Scholar 

  19. A.H. Sofiyev, D. Hui, V.C. Haciyev et al., The nonlinear vibration of orthotropic functionally graded cylindrical shells surrounded by an elastic foundation within first order shear deformation theory. Compos. B Eng. 116, 170–185 (2017)

    Google Scholar 

  20. H.S. Shen, Y. Xiang, Nonlinear response of nanotube-reinforced composite cylindrical panels subjected to combined loadings and resting on elastic foundations. Compos. Struct. 131(nov.), 939–950 (2015)

    Google Scholar 

  21. H.-S. Shen, Y. Xiang, Y. Fan et al., Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical panels resting on elastic foundations in thermal environments. Compos. B Eng. 136, 177–186 (2018)

    Google Scholar 

  22. I. Kreja, R. Schmidt, J.N. Reddy, Finite elements based on a first-order shear deformation moderate rotation shell theory with applications to the analysis of composite structures. Int. J. Non Linear Mech. 32(6), 1123–1142 (1997)

    MATH  Google Scholar 

  23. G. Friesecke, R.D. James, S. Müller, The Föppl–von Kármán plate theory as a low energy Γ-limit of nonlinear elasticity. C. R. Math. 335(2), 201–206 (2002)

    MathSciNet  MATH  Google Scholar 

  24. G.G. Sheng, X. Wang, G. Fu et al., The nonlinear vibrations of functionally graded cylindrical shells surrounded by an elastic foundation. Nonlinear Dyn. 78(2), 1421–1434 (2014)

    MathSciNet  Google Scholar 

  25. A.G. Shah, T. Mahmood, M.N. Naeem et al., Vibrations of functionally graded cylindrical shells based on elastic foundations. Acta Mech. 211(3–4), 293–307 (2009)

    MATH  Google Scholar 

  26. A.G. Shah, T. Mahmood, M.N. Naeem et al., Vibrational study of fluid-filled functionally graded cylindrical shells resting on elastic foundations. ISRN Mech. Eng. 2011, 1–13 (2011)

    Google Scholar 

  27. M.N. Naeem, S. Kanwal, A.G. Shah et al., Vibration characteristics of ring-stiffened functionally graded circular cylindrical shells. ISRN Mech. Eng. 2012, 1–13 (2012)

    Google Scholar 

  28. M. Asgari, Two dimensional functionally graded material finite thick hollow cylinder axisymmetric vibration mode shapes analysis based on exact elasticity theory. J. Theor. Appl. Mech. 45(2), 3–20 (2015)

    MATH  Google Scholar 

  29. C. Betts, Benefits of metal foams and developments in modelling techniques to assess their materials behaviour: a review. Mater. Sci. Technol. 28(2), 129–143 (2013)

    Google Scholar 

  30. A. Hassani, A. Habibolahzadeh, H. Bafti, Production of graded aluminum foams via powder space holder technique. Mater. Des. 40, 510–515 (2012)

    Google Scholar 

  31. M.R. Barati, A.M. Zenkour, Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech. Adv. Mater. Struct. 26(18), 1580–1588 (2018)

    Google Scholar 

  32. S.C. Tjong, Recent progress in the development and properties of novel metal matrix nanocomposites reinforced with carbon nanotubes and graphene nanosheets. Mater. Sci. Eng. R Rep. 74(10), 281–350 (2013)

    Google Scholar 

  33. K.S. Novoselov, A.K. Geim, S. Morozov et al., Electric field effect in atomically thin carbon films. Science New York, (N.Y.) 306, 666–669 (2004)

    Google Scholar 

  34. A.A. Balandin, S. Ghosh, W. Bao et al., Superior thermal conductivity of single-layer graphene. Nano Lett. 8(3), 902–907 (2008)

    ADS  Google Scholar 

  35. S. Stankovich, D.A. Dikin, G.H.B. Dommett et al., Graphene-based composite materials. Nature 442(7100), 282–286 (2006)

    ADS  Google Scholar 

  36. D. Liu, S. Kitipornchai, W. Chen et al., Three-dimensional buckling and free vibration analyses of initially stressed functionally graded graphene reinforced composite cylindrical shell. Compos. Struct. 189, 560–569 (2018)

    Google Scholar 

  37. Y.H. Dong, Y.H. Li, D. Chen et al., Vibration characteristics of functionally graded graphene reinforced porous nanocomposite cylindrical shells with spinning motion. Compos. B Eng. 145, 1–13 (2018)

    Google Scholar 

  38. J. Yang, D. Chen, S. Kitipornchai, Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev–Ritz method. Compos. Struct. 193, 281–294 (2018)

    Google Scholar 

  39. M. Song, S. Kitipornchai, J. Yang, Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 159, 579–588 (2017)

    Google Scholar 

  40. M. Song, J. Yang, S. Kitipornchai, Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. B Eng. 134, 106–113 (2018)

    Google Scholar 

  41. M. Song, J. Yang, S. Kitipornchai et al., Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int. J. Mech. Sci. 131–132, 345–355 (2017)

    Google Scholar 

  42. H.-S. Shen, Y. Xiang, Y. Fan, Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical shells in thermal environments. Compos. Struct. 182, 447–456 (2017)

    Google Scholar 

  43. S. Blooriyan, R. Ansari, A. Darvizeh et al., Postbuckling analysis of functionally graded graphene platelet-reinforced polymer composite cylindrical shells using an analytical solution approach. Appl. Math. Mech. 40(7), 1001–1016 (2019)

    MathSciNet  MATH  Google Scholar 

  44. R. Ansari, J. Torabi, Semi-analytical postbuckling analysis of polymer nanocomposite cylindrical shells reinforced with functionally graded graphene platelets. Thin Walled Struct. 144, 106248 (2019)

    Google Scholar 

  45. D. Shahgholian-Ghahfarokhi, M. Safarpour, A. Rahimi, Torsional buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (GPLs). Mech. Based Des. Struct. Mach. 2019, 1–22 (2019)

    Google Scholar 

  46. S. Kitipornchai, D. Chen, J. Yang, Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 116, 656–665 (2017)

    Google Scholar 

  47. A.P. Roberts, E.J. Garboczi, Elastic moduli of model random three-dimensional closed-cell cellular solids. Acta Mater. 49(2), 189–197 (2001)

    ADS  Google Scholar 

  48. H. Li, F. Pang, X. Miao et al., Jacobi–Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions: a unified formulation. Comput. Math Appl. 77(2), 427–440 (2019)

    MathSciNet  MATH  Google Scholar 

  49. B. Qin, K. Choe, T. Wang et al., A unified Jacobi–Ritz formulation for vibration analysis of the stepped coupled structures of doubly-curved shell. Compos. Struct. 220, 717–735 (2019)

    Google Scholar 

  50. S. Sun, D. Cao, Q. Han, Vibration studies of rotating cylindrical shells with arbitrary edges using characteristic orthogonal polynomials in the Rayleigh–Ritz method. Int. J. Mech. Sci. 68, 180–189 (2013)

    Google Scholar 

  51. Y. Qu, X. Long, G. Yuan et al., A unified formulation for vibration analysis of functionally graded shells of revolution with arbitrary boundary conditions. Compos. B Eng. 50, 381–402 (2013)

    Google Scholar 

  52. Y. Cao, R. Zhong, D. Shao et al., Dynamic analysis of rectangular plate stiffened by any number of beams with different lengths and orientations. Shock Vib. 2019, 1–22 (2019)

    Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Grant Nos. 51705537) and the Natural Science Foundation of Hunan Province of China (2018JJ3661). The authors also gratefully acknowledge the supports from State Key Laboratory of High Performance Complex Manufacturing, Central South University, China (Grant No. ZZYJKT2018-11).

Author information

Authors and Affiliations

  1. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha, 410083, People’s Republic of China

    Zhengxiong Chen, Ailun Wang, Qingshan Wang & Rui Zhong

  2. Key Laboratory of Traffic Safety on Track, Ministry of Education, School of Traffic and Transportation Engineering, Central South University, Changsha, 410075, People’s Republic of China

    Bin Qin

  3. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Central South University, Changsha, 410075, People’s Republic of China

    Bin Qin

  4. National and Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Central South University, Changsha, 410075, People’s Republic of China

    Bin Qin

Authors
  1. Zhengxiong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ailun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bin Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qingshan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rui Zhong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Qingshan Wang or Rui Zhong.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix

Appendix

The specific expressions of the stiffness matrix K can be written as

$$ {\mathbf{K}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{ 1 , 1} } & {{\mathbf{K}}_{1,2} } & {{\mathbf{K}}_{1,3} } & {{\mathbf{K}}_{ 1 , 4} } & {{\mathbf{K}}_{1,5} } \\ {{\mathbf{K}}_{ 1 , 2}^{\text{T}} } & {{\mathbf{K}}_{2,2} } & {{\mathbf{K}}_{2,3} } & {{\mathbf{K}}_{ 2 , 4} } & {{\mathbf{K}}_{2,5} } \\ {{\mathbf{K}}_{ 1 , 3}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 3}^{\text{T}} } & {{\mathbf{K}}_{3,3} } & {{\mathbf{K}}_{ 3 , 4} } & {{\mathbf{K}}_{3,5} } \\ {{\mathbf{K}}_{ 1 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 3 , 4}^{\text{T}} } & {{\mathbf{K}}_{ 4 , 4} } & {{\mathbf{K}}_{ 4 , 5} } \\ {{\mathbf{K}}_{ 1 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 2 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 3 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 4 , 5}^{\text{T}} } & {{\mathbf{K}}_{ 5 , 5} } \\ \end{array} } \right] $$
$$ {\mathbf{K}}_{i.j} = {\mathbf{K}}_{i.j}^{u} + {\mathbf{K}}_{i.j}^{V} + {\mathbf{K}}_{i.j}^{f} $$
$$ {\mathbf{K}}_{1,1}^{\text{u}} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{4}{{L^{2} }}A_{11} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma } + A_{66} u_{,\theta } \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{u}}}}{\partial \theta } + \frac{4}{L}A_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{1,2}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}A_{12} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \theta } + \frac{2}{L}A_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma } + \frac{4}{{L^{2} }}A_{16} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \varsigma }{\text{ + A}}_{26} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{1,4}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {\frac{4}{{L^{2} }}B_{11} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + B_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta } + \frac{2}{L}B_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }{ + }\frac{2}{L}{\text{B}}_{16} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{u}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{1,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left[ {\frac{2}{L}B_{12} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{2}{L}B_{66} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{4}{{L^{2} }}B_{16} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma }{\text{ + B}}_{26} \frac{{\partial {\mathbf{u}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta }} \right]{\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{2,2}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {A_{22} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \theta } + \frac{4}{{L^{2} }}A_{66} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma } + \frac{4}{L}A_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{v}}}}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{2,4}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}B_{12} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + \frac{2}{L}B_{66} + B_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }{ + }\frac{4}{{L^{2} }}{\text{B}}_{16} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{2,5}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {B_{22} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{4}{{L^{2} }}B_{66} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{2}{L}B_{26} \frac{{\partial {\mathbf{v}}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma }{ + }\frac{2}{L}{\text{B}}_{26} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{v}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{3,3}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \theta }\frac{{\partial {\mathbf{w}}}}{\partial \theta } + \frac{4}{{L^{2} }}k_{s} A_{55} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{w}}}}{\partial \varsigma } + \frac{4}{L}k_{s} A_{45} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }\frac{{\partial {\mathbf{w}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{3,4}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {\frac{2}{L}k_{s} A_{55} {\varvec{\upphi}}_{x}^{T} \frac{{\partial {\mathbf{w}}}}{\partial \varsigma } + k_{s} A_{45} {\varvec{\upphi}}_{x}^{T} \frac{{\partial {\mathbf{w}}}}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{3,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \theta }{\varvec{\upphi}}_{\theta } + \frac{2}{L}k_{s} A_{45} \frac{{\partial {\mathbf{w}}^{T} }}{\partial \varsigma }{\varvec{\upphi}}_{\theta } } \right){\text{d}}\theta } } {\text{d}}\varsigma $$
$$ {\mathbf{K}}_{4,4}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{55} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} + \frac{4}{{L^{2} }}D_{11} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + D_{66} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta } + \frac{4}{L}D_{16} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \theta }} \right){\text{d}}\theta } } {\text{d}}\varsigma $$
$$ {\mathbf{K}}_{4,5}^{u} { = }\frac{L}{2}\int_{{{ - }1}}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{45} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{\theta } + D_{66} \frac{2}{L}\frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + D_{16} \frac{4}{{L^{2} }}\frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{x} }}{\partial \varsigma } + D_{26} \frac{{\partial {\varvec{\upphi}}_{x}^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{5,5}^{u} { = }\frac{L}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left( {k_{s} A_{44} {\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } + D_{22} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \theta }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta } + \frac{4}{{L^{2} }}D_{66} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \varsigma } + \frac{4}{L}D_{26} \frac{{\partial {\varvec{\upphi}}_{\theta }^{T} }}{\partial \varsigma }\frac{{\partial {\varvec{\upphi}}_{\theta } }}{\partial \theta }} \right){\text{d}}\theta {\text{d}}\varsigma } } $$
$$ {\mathbf{K}}_{1,1}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{u} \left. {{\mathbf{u}}^{T} {\mathbf{u}}} \right|_{x = 0} + k_{u} \left. {{\mathbf{u}}^{T} {\mathbf{u}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } \quad {\mathbf{K}}_{2,2}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{\theta } \left. {{\mathbf{v}}^{T} {\mathbf{v}}} \right|_{x = 0} + k_{\theta } \left. {{\mathbf{v}}^{T} {\mathbf{v}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$
$$ {\mathbf{K}}_{3,3}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {k_{w} \left. {{\mathbf{w}}^{T} {\mathbf{w}}} \right|_{x = 0} + k_{w} \left. {{\mathbf{w}}^{T} {\mathbf{w}}} \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$
$$ {\mathbf{K}}_{4,4}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {K_{x} \left. {{\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} } \right|_{x = 0} + K_{x} \left. {{\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} } \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$
$$ {\mathbf{K}}_{5,5}^{V} { = }\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {K_{\theta } \left. {{\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } } \right|_{x = 0} + K_{\theta } \left. {{\varvec{\upphi}}_{\theta }^{T} {\varvec{\upphi}}_{\theta } } \right|_{x = L} } \right){\text{d}}z{\text{d}}\theta } } $$
$$ {\mathbf{K}}_{3,3}^{f} { = }\frac{\text{Lr}}{2}\int_{ - 1}^{1} {\int_{0}^{2\pi } {\left[ {K_{r} w^{2} + K_{g} \left( {\frac{4}{{L^{2} }}\frac{{\partial w^{T} }}{\partial \varsigma }\frac{\partial w}{\partial \varsigma } + \frac{{\partial w^{T} }}{r\partial \theta }\frac{\partial w}{r\partial \theta }} \right)} \right]} } {\text{d}}\theta {\text{d}}\varsigma $$

The mass matrix M is given by

$$ {\mathbf{M}}{ = }\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{ 1 , 1} } & 0 & 0 & {{\mathbf{M}}_{ 1 , 4} } & 0 \\ 0 & {{\mathbf{M}}_{ 2 , 2} } & 0 & 0 & {{\mathbf{M}}_{ 2 , 5} } \\ 0 & 0 & {{\mathbf{M}}_{ 3 , 3} } & 0 & 0 \\ {{\mathbf{M}}_{ 1 , 4}^{\text{T}} } & 0 & 0 & {{\mathbf{M}}_{ 4 , 4} } & 0 \\ 0 & {{\mathbf{M}}_{ 2 , 5}^{\text{T}} } & 0 & 0 & {{\mathbf{M}}_{ 5 , 5} } \\ \end{array} } \right] $$
$$ {\mathbf{M}}_{1,1} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{u}}^{T} {\mathbf{u}}_{0} d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{2,2} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{v}}^{T} {\mathbf{v}}d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{3,3} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{0} {\mathbf{w}}^{T} {\mathbf{w}}{\text{d}}\varsigma {\text{d}}\theta } } $$
$$ {\mathbf{M}}_{1,4} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{1} {\mathbf{u}}^{T} {\varvec{\upphi}}_{x} {\text{d}}\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{1,5} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{1} {\mathbf{v}}^{T} {\varvec{\upphi}}_{y} d\varsigma {\text{d}}\theta } } ;\quad {\mathbf{M}}_{4,4} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{2} {\varvec{\upphi}}_{x}^{T} {\varvec{\upphi}}_{x} {\text{d}}\varsigma {\text{d}}\theta } } $$
$$ {\mathbf{M}}_{5,5} = \frac{L}{2}\int_{0}^{2\pi } {\int_{ - 1}^{1} {I_{2} {\varvec{\upphi}}_{y}^{T} {\varvec{\upphi}}_{y} {\text{d}}\varsigma {\text{d}}\theta } } $$
$$ \left( {I_{0} ,I_{1} ,I_{2} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho \left( z \right)\left( {1,\,z,\,z^{2} } \right){\text{d}}z} $$
$$ {\mathbf{G}} =\left[ {{\mathbf{A}}_{\text{mn}} ,{\mathbf{ B}}_{\text{mn}} , { }{\mathbf{C}}_{\text{mn}} {\mathbf{, D}}_{\text{mn}} ,{\mathbf{ E}}_{\text{mn}} } \right]^{\text{T}} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, Z., Wang, A., Qin, B. et al. Investigation on free vibration and transient response of functionally graded graphene platelets reinforced cylindrical shell resting on elastic foundation. Eur. Phys. J. Plus 135, 582 (2020). https://doi.org/10.1140/epjp/s13360-020-00577-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00577-4

Search

Navigation