Alternate backward and forward waves in a coupled nonlinear transmission line

Abstract

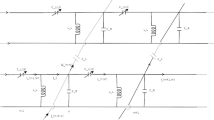
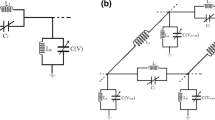
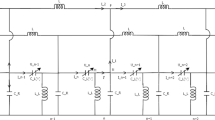
In this work, we investigate backward and forward waves in a coupled nonlinear discrete electrical lattice. It is made of several of the well-known Noguchi electrical transmission line that are transversely coupled to one another by an inductor $L_{2}$. Based on the linear dispersion law, we show that the behavior of this model depends on the wave frequency that it propagates. It can adopt purely right-handed, purely left-handed or composite right-/left-handed behaviors without changing its structure. It appears that for fixed line’s parameters, the network is right-handed for low frequencies and becomes left-handed for high frequencies. It also appears that the increase of the coupling linear inductor induces a decrease of the width of the bandpass filter in the left-handed region while it increases its width in the right-handed region. By means of a method based on the semi-discrete limit and in suitably scaled coordinates, we derive a two-dimensional NLS equation governing the propagation of slowly modulated waves in the network. The exact transverse bright solitary solution is found. Using this solution, we investigate numerically both right-handed and left-handed behaviours of the system and show how to manipulate the coupling inductor to modify the width and the motion of the bright solitary voltage signals in the network.

Appendix: Derivation of two-dimensional NLS equation

To derive the two-dimensional NLS equation describing the propagation of modulated waves in the network, we consider the so-called reductive perturbation method in the semidiscrete approximation, that is, we take the signal voltage in the form given by Eq. (6). It is obvious from this equation that the voltage at any site shifted by an integer j from a reference site (n, m) is given by

$$\begin{aligned} \begin{aligned} V_{n+j,m}(t)=&\varepsilon \left[ A(x+\varepsilon j,y,\tau )\exp (i\theta )+A^{*}(x+\varepsilon j,y,\tau )\exp (-i\theta )\right] +\varepsilon ^2B(x+\varepsilon j,y,\tau ) \\&+\varepsilon ^2 \left[ C(x+\varepsilon j,y,\tau )\exp (2i\theta )+C^{*}(x+\varepsilon j,y,\tau )\exp (-2i\theta )\right] , \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned} \begin{aligned} V_{n,m+j}(t)=\,&\varepsilon \left[ A(x,y+\varepsilon j,\tau )\exp (i\theta )+A^{*}(x,y+\varepsilon j,\tau )\exp (-i\theta )\right] +\varepsilon ^2B(x,y+\varepsilon j,\tau ) \\&+\varepsilon ^2 \left[ C(x,y+\varepsilon j,\tau )\exp (2i\theta )+C^{*}(x,y+\varepsilon j,\tau )\exp (-2i\theta )\right] . \end{aligned} \end{aligned}$$

(20)

To reduce the mathematical intractability of the manipulations involved in the analysis, we assume that $0<\varepsilon \ll 1$ so that Taylor expansions of the following form

$$\begin{aligned} \begin{aligned}&A(x+\varepsilon j,y,\tau )=\,A(x,y,\tau )+\varepsilon j \frac{\partial A}{\partial x}(x,y,\tau ) + \frac{\varepsilon ^2 j^2}{2} \frac{\partial ^2A}{\partial x^2}(x,y,\tau ) + \frac{\varepsilon ^3 j^3}{6} \frac{\partial ^3A}{\partial x^3}(x,y,\tau ) +\cdots \\&A(x,y+\varepsilon j,\tau )=A(x,y,\tau )+\varepsilon j \frac{\partial A}{\partial y}(x,y,\tau ) + \frac{\varepsilon ^2 j^2}{2} \frac{\partial ^2A}{\partial y^2}(x,y,\tau ) + \frac{\varepsilon ^3 j^3}{6} \frac{\partial ^3A}{\partial y^3}(x,y,\tau ) +\cdots \end{aligned} \end{aligned}$$

(21)

are warranted. Here the specific values $j=1$ and $j=-1$ are relevant to Eq. (2). The use of the variables $\theta =k_{1}n+k_{2}m-\omega t,$$x=\varepsilon (n-V_{g1}t)$, $y=\varepsilon (m-V_{g2}t)$ and $\tau =\varepsilon ^2t$ also implies that the time derivative operators are transformed according to

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}=-\omega \frac{\partial }{\partial \theta } + \varepsilon ^2\frac{\partial }{\partial \tau } , \qquad \frac{d^2}{dt^2}=\omega ^2\frac{\partial ^2}{\partial \theta ^2} - 2\varepsilon ^2\omega \frac{\partial ^2}{\partial \tau \partial \theta } +\varepsilon ^4\frac{\partial ^2}{\partial \tau ^2}. \end{aligned} \end{aligned}$$

(22)

Considering the above relations, we obtain the following equation as power series of $\varepsilon$

$$\begin{aligned} \begin{aligned}&\left( -2\,\cos \left( { k_{1}} \right) {{ u_{01}}}^{2}+2\,\cos \left( { k_{1}} \right) { C_{r}}\,{\omega }^{2}-2\,{ C_{r}}\,{ \omega }^{2}+2\,{{ u_{02}}}^{2}\right. \\&\quad \left. +2\,{{ u_{01}}}^{2}-{\omega }^{2}-2\,{{ u_{02}}}^{2}\cos \left( { k_{2}} \right) \right) A \left( x,y,\tau \right) \varepsilon \exp \left( i\theta \right) \\&\quad -2\,i \left( 2\,{ C_{r}}\,\omega \,{ V_{g1}}\,\cos \left( { k_{1}} \right) +\sin \left( { k_{1}} \right) {{ u_{01}}}^{2}-\sin \left( { k_{1}} \right) { C_{r}}\,{\omega }^{2}\right. \\&\quad \left. -\omega \,{ V_{g1}}-2\,{ C_{r}}\,\omega \,{ V_{g1}} \right) {\frac{\partial A(x,y,\tau )}{\partial x}}\varepsilon ^2\exp \left( i\theta \right) \\&\quad -2\,i \left( 2\,{ C_{r}}\,\omega \,{ V_{g2}} \,\cos \left( { k_{1}} \right) +{{ u_{02}}}^{2}\sin \left( { k_{2}} \right) -2\,{ C_{r}}\,\omega \,{ V_{g2}}-\omega \,{ V_{g2}} \right) { \frac{\partial A(x,y,\tau )}{\partial y}}\varepsilon ^2\exp \left( i\theta \right) \\&\quad +2\,i \left( 2\,\cos \left( { k_{1}} \right) { C_{r}}-1-2\,{ C_{r}} \right) \omega \,{\frac{\partial A(x,y,\tau )}{\partial \tau }}\varepsilon ^3\exp \left( i\theta \right) -3\,\beta \,{\omega }^{2} A(x,y,\tau )^{2} \\&\quad A^{*}(x,y,\tau )\varepsilon ^3\exp \left( i\theta \right) \\&\quad + \left( \cos \left( { k_{1}} \right) { C_{r}}\,{\omega }^{2 }-2\,\cos \left( { k_{1}} \right) { C_{r}}\,{{ V_{g1}}}^{2}-\cos \left( {k_{1}} \right) {{ u_{01}}}^{2}\right. \\&\quad \left. +2\,{C_{r}}\,{{V_{g1}}}^{2 }+4\,{ C_{r}}\,\omega \,{V_{g1}}\,\sin \left( { k_{1}} \right) +{{ V_{g1}}}^{2} \right) {\frac{\partial ^{2}A(x,y,\tau )}{\partial {x}^{2}}}\varepsilon ^3\exp \left( i\theta \right) \\&\quad + \left( -2\,{ C_{r}}\,{{ V_{g2}}}^{2}\cos \left( { k_{1}} \right) +2\,{ C_{r}}\,{{ V_{g2}}}^{2}+{{ V_{g2}}}^{ 2}-{{ u_{02}}}^{2}\cos \left( { k_{2}} \right) \right) \frac{ \partial ^{2}A( x,y,\tau )}{\partial {y}^{2}}\varepsilon ^3\exp \left( i\theta \right) \\&\quad -2\,{ V_{g2}}\, \left( -2\,{ C_{r}}\,\omega \,\sin \left( { k_{1}} \right) +2 \,{ C_{r}}\,{ V_{g1}}\,\cos \left( { k_{1}} \right) -2\,{ C_{r}}\, { V_{g1}}-{ V_{g1}} \right) \frac{\partial ^{2}A( x,y,\tau )}{\partial y\partial x}\varepsilon ^3\exp \left( i\theta \right) \\&\quad +\left( 2\alpha \omega ^{2}A^{*}(x,y,\tau )C( x,y,\tau ) +2\alpha \omega ^{2}A(x,y,\tau ) { B} \left( x,y,\tau \right) \right) \varepsilon ^3\exp \left( i\theta \right) \\&\quad +\left( -2\,{{ u_{02}}}^{2}\cos \left( 2\,{ k_{2}} \right) +2\,{{ u_{01}}}^{2}+2\,{{ u_{02}}}^{2}+8\,\cos \left( 2\,{ k_{1}} \right) { C_{r}}\,{\omega }^{2}\right. \\&\quad \left. -2\,\cos \left( 2\,{ k_{1}} \right) {{ u_{01}}}^{2} -8\,{ C_{r}}\,{\omega }^{2}-4\,{\omega }^{2} \right) { C} \left( x,y,\tau \right) \varepsilon ^2\exp \left( i2\theta \right) \\&\quad +\left( 4\,\alpha \,{\omega }^{2}\right) \varepsilon ^2 \left( A \left( x,y,\tau \right) \right) ^{2}\exp \left( i2\theta \right) +B \left( x,y,\tau \right) \varepsilon ^2\exp \left( i0\theta \right) +\cdots . \end{aligned} \end{aligned}$$

(23)

Using this last equation, it follows that $A(x,y,\tau )$ verifies the two-dimensional nonlinear Schrödinger Eq. (7) with coefficients given by Eq. (8).