Abstract
The formalism of Riemannian geometry is applied to study the phase transitions in Nambu–Jona Lasinio (NJL) model. Thermodynamic geometry reliably describes the phase diagram, both in the chiral limit and for finite quark masses. The different thermodynamic geometrical behavior of NJL model and of (2+1) Quantum Chromodynamics at high temperature and small baryon density gives some hints on the connection between chiral symmetry restoration/breaking and deconfinement/confinement regimes.

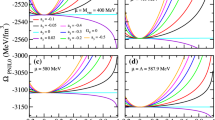
Figure from Ref. [18]

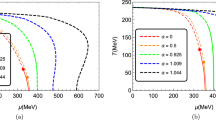
Figure from Ref. [18]











Similar content being viewed by others
References
N. Ay, J. Jost, H. Van Le, L. Schwachhofer, Information Geometry, A Series of Modern Surveys in Mathematics, vol. 64 (Springer, Berlin, 2017)
S. Amari, Information Geometry and Its Applications, Applied Mathematical Sciences, vol. 194 (Springer, Berlin, 2016)
M. Suzuki, Information geometry and statistical manifold. arXiv:1410.3369
R.C. Rao, Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 37, 81–91 (1945)
F. Weinhold, Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 63, 2479, 2484, 2488, 2496 (1975)
George Ruppeiner, Thermodynamics: a Riemannian geometric model. Phys. Rev. A 20, 1608–1613 (1979)
George Ruppeiner, Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 67, 605–659 (1995). [Erratum: Rev. Mod. Phys. 68, 313 (1996)]
George Ruppeiner, Anurag Sahay, Tapobrata Sarkar, Gautam Sengupta, Thermodynamic geometry, phase transitions, and the Widom line. Phys. Rev. E 86, 052103 (2012)
Helge-Otmar May, Peter Mausbach, Riemannian geometry study of vapor-liquid phase equilibria and supercritical behavior of the Lennard–Jones fluid. Phys. Rev. E 85, 031201 (2012)
Helge-Otmar May, Peter Mausbach, George Ruppeiner, Thermodynamic curvature for attractive and repulsive intermolecular forces. Phys. Rev. E 88, 032123 (2013)
Anshuman Dey, Pratim Roy, Tapobrata Sarkar, Information geometry, phase transitions, and the Widom line: magnetic and liquid systems. Phys. A 392, 6341–6352 (2013)
Pankaj Chaturvedi, Anirban Das, Gautam Sengupta, Thermodynamic geometry and phase transitions of dyonic charged AdS black holes. Eur. Phys. J. C 77(2), 110 (2017)
Anurag Sahay, Rishabh Jha, Geometry of criticality, supercriticality and Hawking–Page transitions in Gauss–Bonnet-AdS black holes. Phys. Rev. D 96(12), 126017 (2017)
P. Castorina, M. Imbrosciano, D. Lanteri, Thermodynamic geometry of strongly interacting matter. Phys. Rev. D 98(9), 096006 (2018)
Paolo Castorina, Mauro Imbrosciano, Daniele Lanteri, Thermodynamic geometry and deconfinement temperature. Eur. Phys. J. Plus 134(4), 164 (2019)
George Ruppeiner, Riemannian geometric approach to critical points: general theory. Phys. Rev. E 57, 5135–5145 (1998)
B. Widom, The critical point and scaling theory. Physica 73(1), 107–118 (1974)
George Ruppeiner, Thermodynamic curvature from the critical point to the triple point. Phys. Rev. E 86, 021130 (2012)
H. Janyszek, R. Mrugala, Riemannian geometry and the thermodynamics of model magnetic systems. Phys. Rev. A 39, 6515–6523 (1989)
H. Janyszek, R. Mrugala, Riemannian and finslerian geometry and fluctuations of thermodynamic systems. Advances in Thermodynamics, vol. 3. Nonequilibrium Theory and Extremum Principles, pp. 159–174 (1990)
G. Ruppeiner, Thermodynamic curvature measures interactions. Am. J. Phys. 78, 1170 (2010)
Michele Floris, Hadron yields and the phase diagram of strongly interacting matter. Nucl. Phys. A 931, 103–112 (2014)
S. Das, Identified particle production and freeze-out properties in heavy-ion collisions at RHIC Beam Energy Scan program (2014) [EPJ Web Conf. 90, 08007 (2015)]
L. Adamczyk et al., Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 96(4), 044904 (2017)
Patrick Steinbrecher, The QCD crossover at zero and non-zero baryon densities from Lattice QCD. Nucl. Phys. A 982, 847–850 (2019)
A. Bazavov et al., The QCD equation of state to \({\cal{O}}(\mu _B^6)\) from lattice QCD. Phys. Rev. D 95(5), 054504 (2017)
H. Janyszek, Riemannian geometry and stability of thermodynamical equilibrium systems. J. Phys. A Math. Gen. 23(4), 477–490 (1990)
M.R. Ubriaco, The role of curvature in quantum statistical mechanics. J. Phys. Conf. Ser. 766, 012007 (2016)
R. Ruppeiner, N. Dyjack, A. McAloon, J. Stoops, Solid-like features in dense vapors near the fluid critical point. J. Chem. Phys. 146, 224501 (2017)
Behrouz Mirza, Hosein Mohammadzadeh, Ruppeiner geometry of anyon gas. Phys. Rev. E 78, 021127 (2008)
M.R. Ubriaco, Stability and anyonic behavior of systems with m-statistics. Phys. A Stat. Mech. Appl. 392(20), 4868–4873 (2013)
Anurag Sahay, Tapobrata Sarkar, Gautam Sengupta, On the thermodynamic geometry and critical phenomena of AdS black holes. JHEP 07, 082 (2010)
G. Ruppeiner, P. Mausbach, H.-0. May, Thermodynamic r-diagrams reveal solid-like fluid states. Phys. Lett. A 379(7), 646–649 (2015)
P. Zhuang, J. Hufner, S.P. Klevansky, Thermodynamics of a quark-meson plasma in the Nambu–Jona–Lasinio model. Nucl. Phys. A 576, 525–552 (1994)
T.M. Schwarz, S.P. Klevansky, G. Papp, The Phase diagram and bulk thermodynamical quantities in the NJL model at finite temperature and density. Phys. Rev. C 60, 055205 (1999)
Michael Buballa, NJL model analysis of quark matter at large density. Phys. Rep. 407, 205–376 (2005)
A. Barducci, R. Casalbuoni, G. Pettini, L. Ravagli, A NJL-based study of the QCD critical line. Phys. Rev. D 72, 056002 (2005)
Yue Zhao, Lei Chang, Wei Yuan, Yu-xin Liu, Chiral susceptibility and chiral phase transition in Nambu–Jona–Lasinio model. Eur. Phys. J. C 56, 483–492 (2008)
Aharon Casher, Chiral symmetry breaking in quark confining theories. Phys. Lett. 83B, 395–398 (1979)
Tom Banks, A. Casher, Chiral symmetry breaking in confining theories. Nucl. Phys. B 169, 103–125 (1980)
P. Cea, P. Castorina, Quark confinement and chiral symmetry breaking. Nuovo Cim. A 81, 567 (1984)
S. Digal, E. Laermann, H. Satz, Deconfinement through chiral symmetry restoration in two flavor QCD. Eur. Phys. J. C 18, 583–586 (2001)
H.T. Ding, P. Hegde, F. Karsch, A. Lahiri, S.T. Li, S. Mukherjee, P. Petreczky, Chiral phase transition of (2+1)-flavor QCD. Nucl. Phys. A 982, 211–214 (2019)
Author information
Authors and Affiliations
Corresponding author
Appendices
NJL model with two quarks
To evaluate the scalar curvature R, one needs the derivatives of the potential \(\phi \), up to third order, which can be written in terms of the dynamical generated mass M. Therefore, the solution of the GAP equation uniquely determines all those functions. Indeed, after a straightforward calculation, one gets (a comma indicates partial derivative)
with
and \(n{\pm }\) in Eq. (16).
By deriving Eqs. (24) and (11) and defining
one gets
The calculation of second- and third-order derivatives is straightforward.
Finally, the two-flavor chiral susceptibility, \(\chi \), is defined as [38]
Three flavors
In three-flavor systems, the derivatives of the dynamically generated mass \(M_u=M_d\) and \(M_s\) are
and
where
and \(u\equiv \left\langle {\overline{u}} u\right\rangle \), \(s\equiv \left\langle {\overline{s}} s\right\rangle \).
About the thermodynamic potential \(\phi =-\varOmega \,\beta \), one has
Finally, by defining
the chiral susceptibilities are
and
Rights and permissions
About this article
Cite this article
Castorina, P., Lanteri, D. & Mancani, S. Thermodynamic geometry of Nambu–Jona Lasinio model. Eur. Phys. J. Plus 135, 43 (2020). https://doi.org/10.1140/epjp/s13360-019-00004-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-019-00004-3