Stochastic gene transcription with non-competitive transcription regulatory architecture

Abstract

The transcription factors, such as activators and repressors, can interact with the promoter of gene either in a competitive or non-competitive way. In this paper, we construct a stochastic model with non-competitive transcriptional regulatory architecture and develop an analytical theory that re-establishes the experimental results with an improved data fitting. The analytical expressions in the theory allow us to study the nature of the system corresponding to any of its parameters and hence, enable us to find out the factors that govern the regulation of gene expression for that architecture. We notice that, along with transcriptional reinitiation and repressors, there are other parameters that can control the noisiness of this network. We also observe that, the Fano factor (at mRNA level) varies from sub-Poissonian regime to super-Poissonian regime. In addition to the aforementioned properties, we observe some anomalous characteristics of the Fano factor (at mRNA level) and that of the variance of protein at lower activator concentrations in the presence of repressor molecules. This model is useful to understand the architecture of interactions which may buffer the stochasticity inherent to gene transcription.

Graphical abstract

Appendices

Appendix A

In an attempt to deduce the expressions of mean and the Fano factors, we use a moment generating function which is defined as,

$$\begin{aligned} F(z_{i},t)=\sum _{n=0}^{\infty }z_{i}^{n_{i}}p(n_{i},t) \end{aligned}$$

(15)

Here, $i=1,2,......,6$.

we have,

$$\begin{aligned}&\frac{\partial F(z_{i},t)}{\partial t}\nonumber \\&\quad = \sum _{n=0}^{\infty }z_{i}^{n_{i}}\frac{\partial p(n_{i},t)}{\partial t}\nonumber \\&\quad = k_{1}(z_{1}-1)[lF-z_{1}\frac{\partial F}{\partial z_{1}}-z_{2}\frac{\partial F}{\partial z_{2}}-z_{3}\frac{\partial F}{\partial z_{3}}-z_{4}\frac{\partial F}{\partial z_{4}}]\nonumber \\&\qquad +k_{2}(1-z_{1})\frac{\partial F}{\partial z_{1}}+k_{3}(z_{2}-z_{1})\frac{\partial F}{\partial z_{1}}+k_{4}(z_{1}-z_{2})\frac{\partial F}{\partial z_{2}}\nonumber \\&\qquad +k_{5}(z_{3}-z_{1})\frac{\partial F}{\partial z_{1}}+k_{6}(z_{1}-z_{3})\frac{\partial F}{\partial z_{3}}+k_{7}(z_{4}-z_{3})\frac{\partial F}{\partial z_{3}}\nonumber \\&\qquad +k_{8}(z_{3}-z_{4})\frac{\partial F}{\partial z_{4}}+k_{9}(1-z_{4})\frac{\partial F}{\partial z_{4}}\nonumber \\&\qquad +k_{10}(z_{4}-1)[lF-z_{1}\frac{\partial F}{\partial z_{1}}-z_{2}\frac{\partial F}{\partial z_{2}}-z_{3}\frac{\partial F}{\partial z_{3}}-z_{4}\frac{\partial F}{\partial z_{4}}]\nonumber \\&\qquad +k_{11}(1-z_{2})\frac{\partial F}{\partial z_{2}}+J_{m}(z_{1}z_{5}-z_{2})\frac{\partial F}{\partial z_{2}}+k_{m}(1-z_{5})\frac{\partial F}{\partial z_{5}}\nonumber \\&\qquad +J_{p}(z_{6}-1)z_{5}\frac{\partial F}{\partial z_{5}}+k_{p}(1-z_{6})\frac{\partial F}{\partial z_{6}} \end{aligned}$$

(16)

In steady state, $\frac{\partial F(z_{i},t)}{\partial t}=0$ and for total probability, $F((z_{i}=1,0)=1$

Now, by setting [$\frac{\partial }{\partial z_{1}}(\frac{\partial F}{\partial t})]_{z_{i}=1}=0$, we get $\frac{\partial F}{\partial z_{1}}=f_{1}(say)= <n_{1}> =$ average number of gene at state $G_{a}$.

similarly, by setting [$\frac{\partial }{\partial z_{1}}(\frac{\partial ^{2}F}{\partial z_{1}\partial t})]_{z_{i}=1}=0$ will give $\frac{\partial ^{2}F}{\partial z_{1}^{2}}=f_{11}(say)$ and so on. Proceeding in the same way, we obtain

$$\begin{aligned} f_{5}= <n_{5}> =mean mRNA \end{aligned}$$

and

$$\begin{aligned} f_{6}= & {} <n_{6}>=mean\,Protein\\ Fano\,factor\,(mRNA)= & {} \frac{variance\, of\,mRNA}{mean\, mRNA}\\= & {} \frac{f_{55}+f_{5}-f_{5}^{2}}{f_{5}}\\ Fano factor(Protein)= & {} \frac{variance\,of\,Protein}{mean\, Protein}\\= & {} \frac{f_{66}+f_{6}-f_{6}^{2}}{f_{6}} \end{aligned}$$

Appendix B

The parameters used in Eqs. (2), (3) and (4) are given below

$$\begin{aligned} A= & {} -\frac{b_{19}J_{m}}{b_{20}k_{m}}, B=[\frac{J_{p}}{k_{m}+k_{p}}\\&-\frac{J_{m}J_{p}k_{8}k_{3}^{2}(k_{10}(b_{8}-b_{5}k_{1})-b_{15}k_{1})}{b_{14}k_{p}(k_{m}+k_{p})}\\&+\frac{b_{18}k_{8}(k_{m}+k_{1})}{(b_{8}-b_{4}k_{1})b_{14}(k_{m}+k_{p})}+\frac{b_{19}}{b_{20}}C],\\ C= & {} \frac{b_{17}}{b_{14}(k_{m}+k_{p})}-\frac{J_{m}J_{p}}{k_{m}(k_{m}+k_{p})}\\&-\frac{b_{1}b_{18}k_{8}}{(b_{8}-b_{4}k_{1})b_{14}(k_{m}+k_{p})}-\frac{(b_{2}+k_{m})}{k_{3}}\\&\times (\frac{J_{m}J_{p}k_{3}^{2}(k_{5} (b_{8}-b_{5}k_{1})+b_{15}k_{8})}{b_{14}(k_{m}+k_{p})}\\&+\frac{b_{18}(b_{13}-k_{8}k_{m})}{(b_{8}-b_{4}k_{1})b_{14}(k_{m}+k_{p})}),\\ b_{1}= & {} J_{m}-k_{1}+k_{4}, b_{2}=J_{m}+k_{4}+k_{11},\\ b_{3}= & {} k_{8}+k_{9}+k_{10}, b_{4}=k_{m}+k_{6}+k_{7},\\ b_{5}= & {} k_{p}+k_{6}+k_{7}, b_{6}=k_{1}+k_{2}+k_{3}+k_{5},\\ b_{7}= & {} k_{8}(k_{10}-k_{7}), b_{8}=(k_{6}-k_{1})k_{8},\\ b_{9}= & {} k_{1}(k_{7}k_{9}+k_{6}(k_{8}+k_{9})+k_{6}k_{8}k_{10}),\\ b_{10}= & {} k_{1}(k_{6}+k_{7}+k_{8})-k_{6}k_{8},\\ b_{11}= & {} k_{8}k_{10}+k_{7}(k_{9}+k_{10})+k_{6}b_{3},\\ b_{12}= & {} k_{5}b_{3}-k_{8}k_{10}, b_{13}=k_{1}k_{5}-b_{6}k_{8},\\ b_{14}= & {} k_{3}((-b_{15}((b_{2}+k_{p})(b_{13}-k_{8}k_{p})+b_{1}k_{3}k_{8})\\&+(k_{1}k_{p}+b_{10})(k_{3}k_{8}k_{10}-(b_{2}+k_{p})(b_{12} +k_{5}k_{p})),\\ b_{15}= & {} -b_{5}(b_{3}+k_{p})-b_{7}, b_{16}=-b_{4}(b_{3}+k_{m})-b_{7},\\ b_{17}= & {} J_{m}J_{p}k_{3}(b_{15}(b_{13}-k_{8}k_{p})-(b_{8}-b_{5}k_{1})(b_{12}+k_{5}k_{p})),\\ b_{18}= & {} J_{m}J_{p}k_{3}^{2}((b_{8}-b_{5}k_{1})(b_{3}+b_{4}+k_{p})-b_{15}k_{1}),\\ b_{19}= & {} k_{3}k_{8}(k_{10}(b_{8}-b_{4}k_{1})-(k_{m}+k_{1})b_{16}),\\ b_{20}= & {} (k_{3}(-b_{1}b_{16}k_{8}-k_{10}k_{8}(b_{8}-b_{4}k_{1}))\\&+((b_{8}-b_{4}k_{1})(b_{12}+k_{5}k_{m})\\&-b_{16}(b_{13}-k_{8}k_{m}))(b_{2}+k_{m})). \end{aligned}$$

Appendix C

Expression for mean mRNA and protein levels for transcription without reinitiation is given by

$$\begin{aligned} m^{WTR}=\frac{a_{6}J_{m}}{(a_{6}+a_{5})k_{m}};\quad p^{WTR}=\frac{m^{WTR}\,J_{p}}{k_{p}} \end{aligned}$$

(17)

Fig. 19

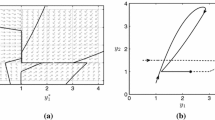
Variation of mean mRNA against GAL keeping aTc = 500 ng ml$^{-1}$ as parameter in (a) and mean mRNA vs $J_{m}$ with aTc = 40 ng ml$^{-1}$ and GAL = 2% as parameter in (b) while other rate constants are chosen from Blake et al. [3]

where $a_{6}=\left( a_{1}k_{1}+k_{6}k_{8}k_{10}\right)$, $a_{5}=a_{1}k_{2}+a_{3}k_{2}+a_{2}k_{1}k_{5}+a_{4}$, $a_{1}=k_{7}k_{9}+k_{6}(k_{8}+k_{9})$, $a_{2}=k_{7}+k_{8}+k_{9}$, $a_{3}=k_{6}k_{10}+k_{7}k_{10}+k_{8}k_{10}$, $a_{4}=k_{5}k_{7}k_{10}+k_{5}k_{8}k_{10}+k_{5}k_{7}k_{9}$,

The expression for the Fano factor at mRNA levels is given by

$$\begin{aligned} FF_{m}^{WTR}=1+\frac{g_{23}k_{8}J_{m}^{2}}{g_{20}k_{m}}+X-m^{WTR} \end{aligned}$$

(18)

where $X=\frac{\begin{array}{ll} &{}g_{22}k_{8}J_{m}^{2}(g_{20}(2g_{19}(g_{1}+k_{m})(g_{3}(k_{m}+k_{1})\\ &{}\quad +k_{1}k_{10})-g_{18}(g_{15}(k_{m}+k_{1})\\ &{}\quad +g_{10}k_{10}))-g_{23}g_{24}) \end{array}}{\begin{array}{ll} &{}(g_{20}J_{m}(-g_{19}(g_{1}+k_{m})(g_{13}-2g_{4}k_{8}J_{m})\\ &{}\quad +(g_{18}J_{m}(-g_{10}(g_{2}+k_{m})-g_{15}k_{1}\\ &{}\quad +g_{25}k_{8})))+g_{20}g_{22}g_{24}k_{m}) \end{array}},$

$$\begin{aligned} g_{25}= & {} 2g_{6}\left( g_{1}\left( k_{7}k_{8}-\left( k_{1}+k_{8}\right) k_{10}\right) -g_{5}k_{5}\right) -g_{8}g_{21},\\ g_{24}= & {} g_{18}J_{m}\left( g_{10}\left( k_{5}k_{m}-k_{8}k_{10}\right) \right. \\&\left. +g_{15}\left( k_{1}k_{5}-k_{8}\left( g_{3}+k_{m}\right) \right) +g_{2}g_{10}k_{5}\right) \\&+g_{19} \left( g_{13}k_{5}-g_{12}k_{8}\right) \left( g_{1}+k_{m}\right) ,\\ g_{23}= & {} 2g_{3}g_{16}\left( k_{m}+k_{1}\right) +g_{11}g_{18}\left( k_{m}+k_{1}\right) \\&+k_{10}\left( 2g_{16}k_{1}+g_{9}g_{18}\right) ,\\ g_{22}= & {} g_{18}\left( k_{8}\left( 2g_{2}g_{6}\left( k_{7}-k_{10}\right) \right. \right. \\&\left. \left. +2\left( g_{5}-g_{2}g_{4}\right) g_{21}\right) J_{m}^{2}-g_{14}J_{m}\right) \\&-g_{16}\left( 2g_{4}k_{8}J_{m}^{2}-g_{13}J_{m}\right) ,\\ g_{21}= & {} 2\left( g_{1}^{2}+g_{3}g_{1}-g_{4}k_{5}\right) ,\\ g_{20}= & {} g_{18}\left( k_{8}\left( g_{9}k_{10}J_{m}-g_{11}J_{m}\left( -g_{3}-k_{m}\right) \right) -g_{14}k_{5}\right) \\&-g_{16}\left( g_{12}k_{8}-g_{13}k_{5}\right) ,\\ g_{19}= & {} J_{m}[k_{8}\left( g_{10}\left( k_{10}-k_{7}\right) -g_{4}g_{15}\right) -g_{10}\left( g_{2}+k_{m}\right) \\&-g_{15}k_{1}],\\ g_{18}= & {} g_{17}k_{8}+g_{13}\left( g_{1}+k_{m}\right) , g_{17}=2J_{m}(g_{3}g_{4}+g_{5}),\\ g_{16}= & {} k_{8}J_{m}\left( g_{9}\left( k_{10}-k_{7}\right) -g_{4}g_{11}\right) +g_{14}\left( g_{1}+k_{m}\right) ,\\ g_{15}= & {} 2g_{1}(g_{8}k_{5}-g_{6}k_{8}k_{10}),\\ g_{14}= & {} J_{m}(g_{11}k_{1}+g_{9}\left( g_{2}+k_{m})\right) ,\\ g_{13}= & {} 2k_{1}J_{m}(\left( -g_{2}-k_{m}\right) -g_{3}),\\ g_{12}= & {} 2J_{m}(g_{3}\left( -g_{3}-k_{m}\right) -k_{1}k_{10}),\\ g_{11}= & {} -g_{7}k_{5}-2g_{2}g_{6}k_{10},\\ g_{10}= & {} 2g_{1}(g_{8}k_{8}-g_{6}\left( \left( g_{2}+g_{3}\right) k_{8}-k_{1}k_{5})\right) ,\\ g_{9}= & {} 2g_{6}\left( k_{1}k_{10}-g_{2}\left( g_{2}+g_{3}\right) \right) -g_{7}k_{8},\\ g_{8}= & {} 2k_{8}g_{5}-2g_{1}\left( \left( g_{1}+g_{2}\right) k_{1}-g_{4}k_{8}\right) ,\\ g_{7}= & {} 4g_{1}\left( g_{5}-g_{2}g_{4}\right) , g_{6}=2\left( g_{1}k_{1}-g_{4}k_{8}\right) ,\\ g_{5}= & {} k_{1}(k_{7}-k_{10}), g_{4}=(k_{6}-k_{1}),\\ g_{3}= & {} (k_{1}+k_{2}+k_{5}),\\ g_{2}= & {} (k_{8}+k_{9}+k_{10}), g_{1}=(k_{6}+k_{7}). \end{aligned}$$

The expression of the Fano factor at protein levels is given by

$$\begin{aligned} FF_{p}^{WTR}= & {} 1+\frac{J_{p}}{k_{m}+k_{p}}-\frac{k_{1}k_{8}J_{m}J_{p}}{h_{1}k_{p}\left( k_{m}+k_{p}\right) }\nonumber \\&+\frac{h_{4}\left( h_{1}k_{8}k_{10}-h_{2}k_{1}k_{8}\right) J_{m}J_{p}}{h_{1}h_{8}k_{p}\left( k_{m}+k_{p}\right) } +Y+Z-p^{WTR}\nonumber \\ \end{aligned}$$

(19)

where

$$\begin{aligned} Y= & {} \frac{\begin{array}{ll} &{}k_{8}J_{m}^{3}J_{p}(h_{11}-g_{24}(k_{10}(2g_{16}k_{1}+g_{9}g_{18})\\ &{}\quad +h_{7}(k_{m}+k_{1})))(h_{3}k_{1}(g_{13}+2(k_{1}-k_{6})k_{8}J_{m})\\ &{}\quad +\frac{h_{9}h_{10}}{g_{20}k_{m}}-h_{4}(2h_{6}(k_{1}-k_{6})k_{8}J_{m}+h_{5})) \end{array}}{\begin{array}{ll} &{}g_{18}h_{8}(k_{m}+k_{p})(g_{20}J_{m}(g_{18}J_{m}(-g_{10}(g_{2}+k_{m})\\ &{}\quad -g_{15}k_{1}+g_{25}k_{8})-g_{19}(g_{1}+k_{m})(2g_{4}k_{8}J_{m}\\ &{}\quad +g_{13}))+g_{22}g_{24}) \end{array}},\\ Z= & {} \frac{2k_{8}\left( h_{3}k_{1}-h_{4}h_{6}\right) J_{m}^{2}J_{p}\left( g_{3}k_{m}+k_{1}\left( g_{3}+k_{10}\right) \right) }{g_{18}h_{8} \left( k_{m}+k_{p}\right) }\\&+\frac{h_{9}k_{8}J_{m}^{2}J_{p}\left( k_{1}\left( 2g_{16}k_{10}+h_{7}\right) +g_{9}g_{18}k_{10}+h_{7}k_{m}\right) }{g_{18}g_{20}h_{8}k_{m}\left( k_{m}+k_{p}\right) },\\ h_{11}= & {} g_{20}\left( 2g_{19}\left( g_{1}+k_{m}\right) \left( g_{3}k_{m}+k_{1}\left( g_{3}+k_{10}\right) \right) \right. \\&\left. -g_{18}\left( g_{15}k_{m}+g_{15}k_{1}+g_{10}k_{10}\right) \right) ,\\ h_{10}= & {} 2k_{8}\left( g_{16}\left( k_{1}-k_{6}\right) +g_{18}\left( g_{2}g_{6}k_{7}-g_{2}g_{6}k_{10}\right. \right. \\&\left. \left. -g_{2}g_{4}g_{21}+g_{5}g_{21}\right) \right) J_{m}+g_{13}g_{16}-g_{14}g_{18},\\ h_{9}= & {} k_{m}\left( h_{4}\left( h_{5}k_{5}-g_{12}h_{6}k_{8}\right) \right. \\&\left. -h_{3}\left( g_{18}k_{8}+k_{1}\left( g_{13}k_{5}-g_{12}k_{8}\right) \right) \right) +g_{18}h_{8},\\ h_{8}= & {} (h_{1}h_{3}-h_{2}h_{4}), h_{7}=2g_{3}g_{16}+g_{11}g_{18},\\ h_{6}= & {} g_{1}+g_{2}+k_{m}+k_{p},\\ h_{5}= & {} (k_{m}+k_{p}+g_{1}+g_{2})g_{13}-g_{18},\\ h_{4}= & {} g_{4}k_{8}-k_{1}\left( g_{1}+k_{p}\right) , h_{3}=k_{8}(k_{7}-k_{10})\\&-(g_{1}+k_{p})(g_{2}+k_{p}),\\ h_{2}= & {} k_{5}(g_{2}+k_{p})-k_{8}k_{10}, h_{1}=k_{1}k_{5}-k_{8}(g_{3}+k_{p}) \end{aligned}$$

Appendix D

In Fig. 17a, b, it is seen that mean mRNA and mean protein in case of transcriptional reinitiation-based network is greater than that of without reinitiation network. But the mean values against other variables like $J_{m}$ shows that $m^{WR}$ can be high or less than $m^{WTR}$ as shown in figure below.

Fig. 20

Relative Error for: a fitting of curves when aTc is fixed at 500 ng/ml. Blake et al. [3] model offers MSE = 7.108, while our proposed model fits quite nicely with the experimentally observed data with a minimize MSE = 0.873 b fitting of curves when aTc is fixed at 500 ng/ml. Blake et al. [3] model offers MSE = 2.918, while our proposed model fits better with the experimentally observed data with a reduced MSE = 2.105

Figures 17a and 19a show that $m^{WR}$ is higher than $m^{WTR}$ keeping GAL and aTc as parameter, respectively, but Fig.  19b shows a different scenario where we keep both GAL and aTc fixed. It is verified that, the slope of mean mRNA curve becomes high against $J_{m}$ for a higher concentration of GAL keeping aTc fixed. On the other hand, if we increase aTc for a fixed GAL the slope of the curve goes high against $J_{m}$. Imposing the condition $m^{WR}=m^{WTR}$, we have found a critical value of $J_{m}$ given by

$$\begin{aligned} J_{m}^{cr}=\frac{k_{3}\left( B_{7}-b_{11}k_{11}\right) -\left( b_{9}+B_{7}\right) k_{r}}{b_{9}+B_{7}} \end{aligned}$$

(20)

where, $B_{7}=a_{2}k_{1}k_{5}+a_{4}+b_{11}k_{2}$ and $k_{r}=k_{4}+k_{11}$ other parameters are supplied earlier.

Appendix E

Model fitting parameters: We proposed an analytical model that fits very much to the experimental data as supplied by Blake et al. [3]. The parameters are chosen from the supplementary material of [3]. The form of parameters $k_{1}$ and $k_{2}$ as functions of GAL are determined from an exact analytical treatment as described in the main text. While for the best estimates of other parameters are revised through trial and error to minimize the sum of squared error (SSE) and the mean square error (MSE). We also show the relative percentile error (RE), in Fig. 20a, b for the fitting of each of the data points, which is given by

$$\begin{aligned} RE=\frac{y_{a}-y_{e}}{y_{e}} . 100\% \end{aligned}$$

(21)

where, a stands for analytical and e stands for experimental.

Fig. 21

Relative Sensitivity of the Fano factor as functions of fitting parameters

Fig. 22

Table for the errors in curve fitting, estimated parameter values and their uncertainties

Uncertainty in fitted parameters : The uncertainty of the parameter estimates, is generally expressed by the mean square errors, is proportional to the SSE and inversely proportional to the square of the sensitivity coefficient of the model parameters [53]. The mean square fitting error is

$$\begin{aligned} \sigma ^{2}=\frac{1}{n-k}\sum _{i=1}^{n}(y_{a}-y_{e})^{2}=\frac{Sum of squared error}{(n-k)} \end{aligned}$$

(22)

n is the number of observations and k is the number of parameters being determined.

The sensitivity ($\mathscr {S}$) of a function f(k) over the parameter k is given by

$$\begin{aligned} \mathscr {S}=\frac{k}{f(k)}.\frac{\partial f(k)}{\partial k} \end{aligned}$$

(23)

We obtain the sensitivity of the Fano factor (protein) over the fitting parameters and calculate MSE of each parameter keeping others as constant.

$$\begin{aligned} MSE=\frac{\sigma ^{2}}{\sum _{i=1}^{n}[\frac{\partial f(k)}{\partial k}]^{2}} \end{aligned}$$

(24)

where the denominator is the coefficient of sensitivity, squared and summed over all observations.

The GAL is the most sensitive parameter and e is the least in order (see Fig. 21). We found that, the Fano factor is sensitive within a small range of values of these parameters and with the best parameter estimation and minimization of errors (see Fig. 22) support the robustness of our result. The square root of the MSE is the standard deviation, and the approximate 95% confidence interval for k is [53]

$$\begin{aligned} {[}k]_{95\%}=\kappa \pm 2\surd MSE \end{aligned}$$

(25)

$\kappa$ is the best estimate value of parameter k.