Rayleigh method adapted for the study of the optical response of natural photonic structures

Abstract

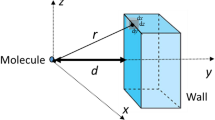
To study the electromagnetic response of natural structures that exhibit interesting optical properties, we developed a computational tool to solve the problem of electromagnetic scattering by a rough interface between two isotropic media, based on the Rayleigh method. The key aspect of the developed formalism is its capability of introducing the interface profile within the code by means of a digitalized image of the structure, which can be either obtained from an electron microscopy image or simply by design according to the complexity of the scattering surface. As application examples, we show the results obtained for surfaces taken directly from microscopy images of two different biological species. This approach constitutes a fundamental step in order to model the electromagnetic response of natural photonic structures.

Graphic Abstract

Appendices

Appendix A

We give here the explicit expressions for the kernel functions of Eqs. (7) and (8).

$$\begin{aligned} K^r(\alpha ',\alpha )=M_{\alpha ,\alpha '}\;D[\alpha '-\alpha ,\beta _{\alpha ' }^{(2)}-\beta _{\alpha }^{(1)}], \end{aligned}$$

(A.1)

$$\begin{aligned} K^t(\alpha ',\alpha )=M_{\alpha ',\alpha }\;D[\alpha '-\alpha ,\beta _{\alpha }^{(2)}-\beta _{\alpha '}^{(1)}], \end{aligned}$$

(A.2)

where

$$\begin{aligned} M_{\alpha ,\alpha '}=\frac{\left( 1-\frac{\gamma _2}{\gamma _1}\right) \left( \alpha \alpha '+\beta _{\alpha ' }^{(2)}\beta _{\alpha }^{(1)}\right) +k_0^2\left( \frac{\gamma _2}{\gamma _1}\nu _1^2-\nu _2^2\right) }{\beta _{\alpha ' }^{(2)}-\beta _{\alpha }^{(1)}},\nonumber \\ \end{aligned}$$

(A.3)

and

$$\begin{aligned} D\left[ u,v \right] =\frac{1}{2\pi }\int \limits _{-\infty }^{+\infty }dxe^{-iux}e^{-ivg(x)}. \end{aligned}$$

(A.4)

$D\left[ u,v \right]$ is the Fourier transform of $e^{-ivg(x)}$. Taking into account the particular expression for g(x) given in Eq. (1), it can be shown by elementary calculations that:

$$\begin{aligned} D\left[ u,v \right] =\delta (u)-\frac{1}{\pi u}\sin \left( \frac{a}{2}u\right) +D'\left[ u,v \right] , \end{aligned}$$

(A.5)

where

$$\begin{aligned} D'\left[ u,v \right] =\frac{1}{2\pi }\int \limits _{-\frac{a}{2}}^{+\frac{a}{2}}dxe^{-iux}e^{-ivg(x)}. \end{aligned}$$

(A.6)

The inhomogeneity in Eq. (7) is

$$\begin{aligned} K(\alpha ',\alpha _0)=N_{\alpha _0,\alpha '}\;2\pi \;D \left[ \alpha '-\alpha _0,\beta _{\alpha ' }^{(2)}+\beta _{0 }^{(1)} \right] ,\quad \end{aligned}$$

(A.7)

where

$$\begin{aligned} N_{\alpha _0,\alpha '}=\frac{\left( 1-\frac{\gamma _2}{\gamma _1}\right) \left( \alpha '\alpha _0-\beta _{\alpha ' }^{(2)}\beta _{0 }^{(1)}\right) +k_0^2\left( \frac{\gamma _2}{\gamma _1}\nu _1^2-\nu _2^2\right) }{\beta _{\alpha ' }^{(2)}+\beta _{0 }^{(1)}}.\nonumber \\ \end{aligned}$$

(A.8)

Appendix B

Substituting $R(\alpha )$ from Eq. (9) into Eq. (7), and taking into account the expression of Eq. (A.5) and that $R^{(0)}=-N_{\alpha _0,\alpha _0}/M_{\alpha _0,\alpha _0}$, Eq. (13) is obtained. The expression of $b_R(\alpha ')$ in the right-hand side of Eq. (13) is:

$$\begin{aligned}&b_R(\alpha ')=2\frac{\sin (\frac{a}{2}(\alpha ' -\alpha _0 ))}{\alpha ' -\alpha _0}\left( N_{\alpha _0, \alpha ' }+R^{(0)}M_{\alpha _0, \alpha ' } \right) \nonumber \\&-2\pi \Bigg (N_{\alpha _0, \alpha ' }D'\left[ \alpha ' -\alpha _0,\beta _{\alpha '}^{(2)}+\beta _{0}^{(1)} \right] \nonumber \\&+ R^{(0)}M_{\alpha _0, \alpha ' }D'\left[ \alpha ' -\alpha _0,\beta _{\alpha '}^{(2)}-\beta _{0}^{(1)} \right] \Bigg ). \end{aligned}$$

(B.1)

Analogously, substituting $T(\alpha )$ from Eq. (10) into Eq. (8) and taking into account that $T^{(0)}=-\frac{\gamma _2}{\gamma _1}2\beta _0^{(1)}/M_{\alpha _0,\alpha _0}$, Eq. (14) is obtained, where $b_T(\alpha ')$ is given by:

$$\begin{aligned}&b_T(\alpha ')=-2\pi T^{(0)}M_{\alpha ',\alpha _0 }\Bigg \{ D'\left[ \alpha ' -\alpha _0,\beta _{0}^{(2)}-\beta _{\alpha '}^{(1)} \right] \nonumber \\&\quad -\frac{\sin (\frac{a}{2}(\alpha ' -\alpha _0 ))}{\pi (\alpha ' -\alpha _0)}\Bigg \}. \end{aligned}$$

(B.2)